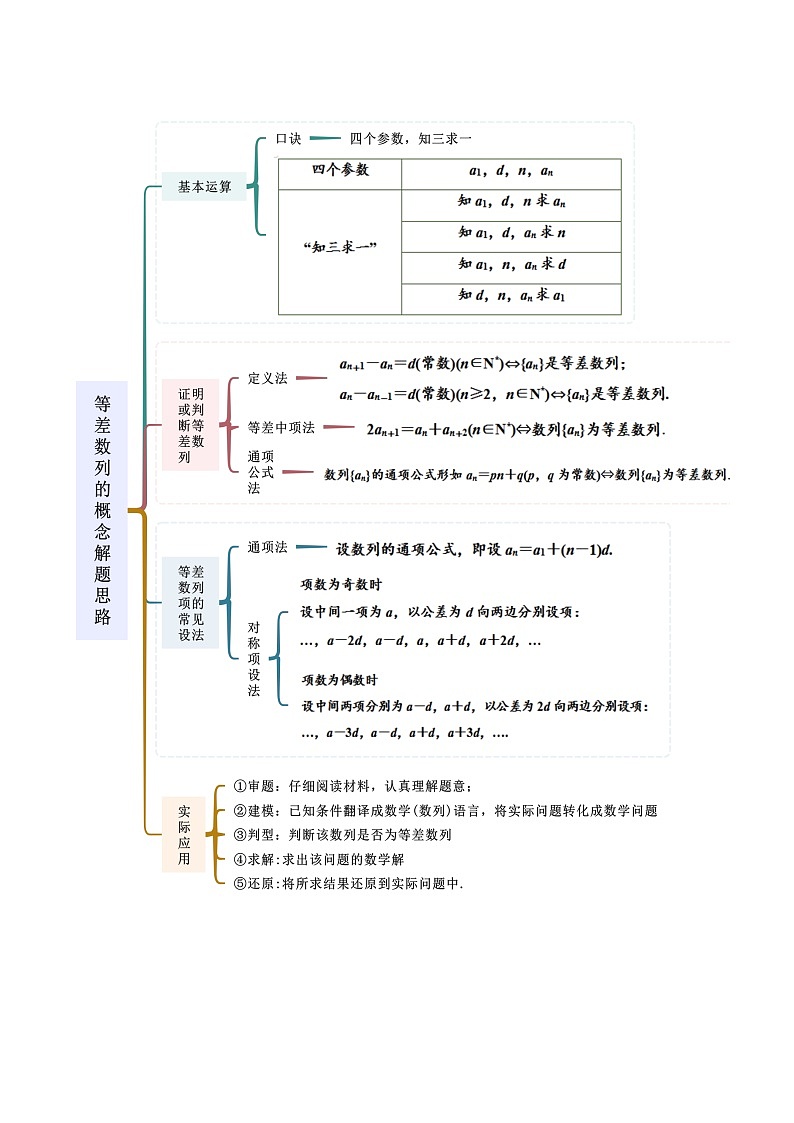
人教A版 (2019)选择性必修 第二册第四章 数列4.1 数列的概念精品课后作业题

这是一份人教A版 (2019)选择性必修 第二册第四章 数列4.1 数列的概念精品课后作业题，文件包含人教版高中数学选择性必修二精讲精练421等差数列的概念精讲原卷版docx、人教版高中数学选择性必修二精讲精练421等差数列的概念精讲解析版docx等2份试卷配套教学资源，其中试卷共27页， 欢迎下载使用。

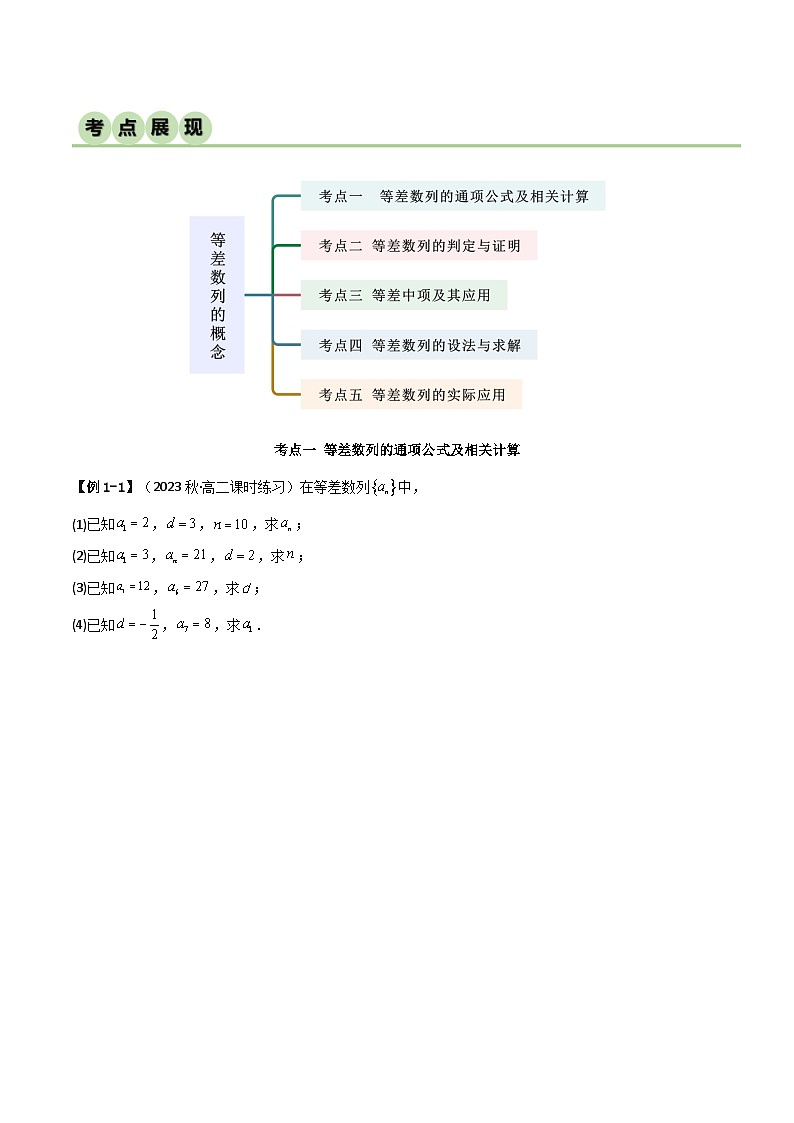
考点一 等差数列的通项公式及相关计算
【例1-1】（2023秋·高二课时练习）在等差数列中，
(1)已知，，，求；
(2)已知，，，求；
(3)已知，，求；
(4)已知，，求．
【例1-2】（2023·上海 ）已知等差数列中，且，为方程的两个实根．
(1)求此数列的通项公式；
(2)268是不是此数列中的项？若是，是第多少项？若不是，说明理由．
【一隅三反】
1．（2023秋·高二课时练习）在等差数列中，
(1)已知，，求；
(2)已知，，求d；
(3)已知，，，求n.
(4)已知，，求，；
(5)已知，，求；
(6)已知，，求．
(7)已知，，求首项与公差；
(8)已知，，求通项．
2（2023云南）在等差数列中，，．
(1)求的通项公式；
(2)判断96是不是数列中的项？
3．（2023春·高二课时练习）已知为等差数列，且以，，若在每相邻两项之间插入三个数，使它和原数列的数构成一个新的等差数列，求：
(1)原数列的第12项是新数列的第几项？
(2)新数列的第29项是原数列的第几项？
考点二 等差数列的判定与证明
【例2-1】（2023·全国·高二课堂例题）判断下列数列是否为等差数列：
(1)1，1，1，1，1；
(2)4，7，10，13，16；
(3)－3，－2，－1，1，2，3．
【例2-2】（2023秋·江苏南通 ）已知数列中，，.
(1)求的值，并猜想数列的通项公式；
(2)证明数列是等差数列.
【一隅三反】
1．（2023·全国·高二课堂例题）判断以下数列是否是等差数列？如果是，指出公差；如果不是，说明理由．
(1)7，13，19，25，31；
(2)2，4，7，11；
(3)．
2.（2023·黑龙江）在数列中，是1与的等差中项，求证：数列是等差数列.
3．（2023·全国·高二专题练习）在数列中4，，．求证：数列{}是等差数列；
4．（2022秋·黑龙江齐齐哈尔·高二齐齐哈尔市恒昌中学校校考期末）设数列的前n项和，满足，且
(1)证明：数列为等差数列
(2)求的通项公式
考点三 等差中项及其应用
【例3-1】（2023春·安徽芜湖 ）已知数列是等差数列，，则（ ）
A．9B．0C．-3D．-6
【例3-2】（2023春·高二课时练习）在等差数列中，，则（ ）
A．36B．48C．60D．72
【例3-3】（ ）
A．B．C．D．
【例3-4】（2023北京）在等差数列中，若，则 .
【一隅三反】
1．（2023春·浙江杭州·高二校联考期中）在等差数列中，若，则（ ）
A．B．1C．0D．
2．（2023·全国·高二专题练习）等差数列中，，，则该数列的公差为（ ）
A．B．2C．D．3
3．（2023春·广西崇左·高二校考期中）若a是4+m，4-m的等差中项，则a=
4．（2023春·西藏日喀则·高二统考期末）在等差数列中，若，则 .
5．（2023·高二课时练习）若正项等差数列满足：，则的最小值为 .
6．（2023春·江西上饶·高二校联考期中）已知，成等差数列，则 .
考点四 等差数列的设法与求解
【例4-1】（2023高二课时练习）已知三个数成等差数列并且数列是递增的，它们的和为18，平方和为116，求这三个数.
【例4-2】（2023春·高二课时练习）已知4个数成等差数列，它们的和为20，中间两项之积为24，求这个4个数．
【一隅三反】
1．（2023湖北）（多选）已知四个数成等差数列，它们的和为28，中间两项的积为40，则这四个数依次为（ ）
A．-2，4，10，16B．16，10，4，-2
C．2，5，8，11D．11，8，5，2
2．（2023湖北）已知5个数成等差数列,它们的和为5,平方和为165,求这5个数.
3．（2023·河南）已知五个数成等差数列，它们的和为5，平方和为，求这5个数．
考点五 等差数列的实际应用
【例5-1】（2023春·江西萍乡·高二萍乡市安源中学校考期末）某市出租车的计价标准为1.2元/km，起步价为10元，即最初的4km（不含4km）计费10元.如果某人乘坐该市的出租车去往16km处的目的地，且一路畅通，等候时间为0，需要支付的车费为（ ）
A．23.2B．24.4C．25.6D．26.8
【例5-2】（2023春·安徽宿州·高二江西省泰和中学校联考期中）《孙子算经》是中国古代重要的数学著作，上面记载了一道有名的“孙子问题”，后来南宋数学家秦九韶在《算书九章·大衍求一术》中将此问题系统解决．“大衍求一术”属于现代数论中的一次同余式组问题，后传入西方，被称为“中国剩余定理”．现有一道同余式组问题：将正整数中，被4除余3且被6除余1的数，按由小到大的顺序排成一列数，则（ ）
A．115B．117C．119D．121
【一隅三反】
1．（2023春·湖北武汉·高二校联考期中）《周髀算经》中有这样一个问题：冬至、小寒、大寒、立春、雨水、惊蛰、春分、清明、谷雨、立夏、小满、芒种这十二个节气，自冬至日起，其日影长依次成等差数列，立春当日日影长为9.5尺，春分当日日影长为6尺，则小满当日日影长为（ ）
A．尺B．13尺C．尺D．尺
2．（2023春·河南驻马店·高二河南省驻马店高级中学校考期中）“中国剩余定理”又称“孙子定理”，1852年英国来华传教士伟烈亚力将《孙子算经》中“物不知数”问题的解法传至欧洲.1874年英国数学家马西森指出此法符合1801年由高斯得出的关于同余式解法的一般性定理，因而西方称之为“中国剩余定理”，“中国剩余定理”讲的是一个关于同余的问题．现有这样一个问题：将正整数中能被3除余1且被2除余1的数按由小到大的顺序排成一列，构成数列，则（ ）
A．55B．49C．43D．37
3．（2023·全国·高二专题练习）2022北京冬奥会开幕式将我国二十四节气融入倒计时，尽显中国人之浪漫．倒计时依次为：大寒、小寒、冬至、大雪、小雪、立冬、霜降、寒露、秋分、白露、处暑、立秋、大暑、小暑、夏至、芒种、小满、立夏、谷雨、清明、春分、惊蛰、雨水、立春，已知从冬至到夏至的日影长等量减少，若冬至、立冬、秋分三个节气的日影长之和为31.5寸，问大雪、寒露的日影长之和为（ ）
A．21寸B．20.5寸C．20寸D．19.5寸