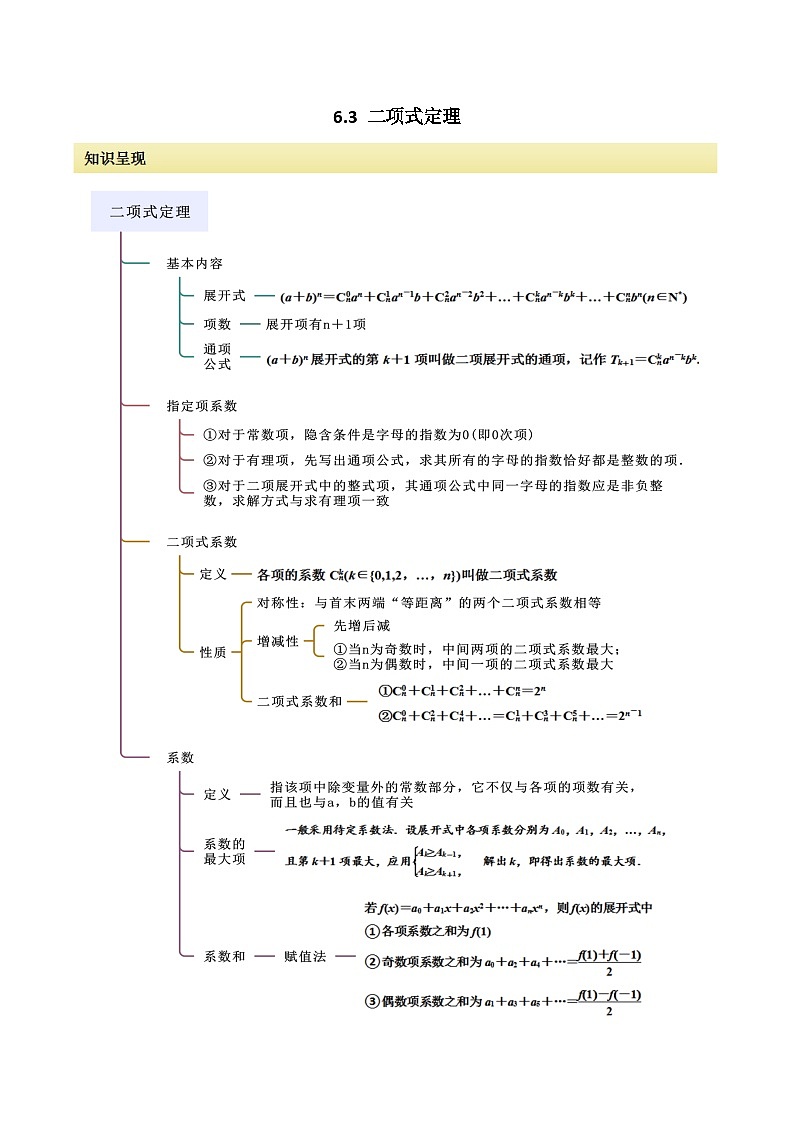

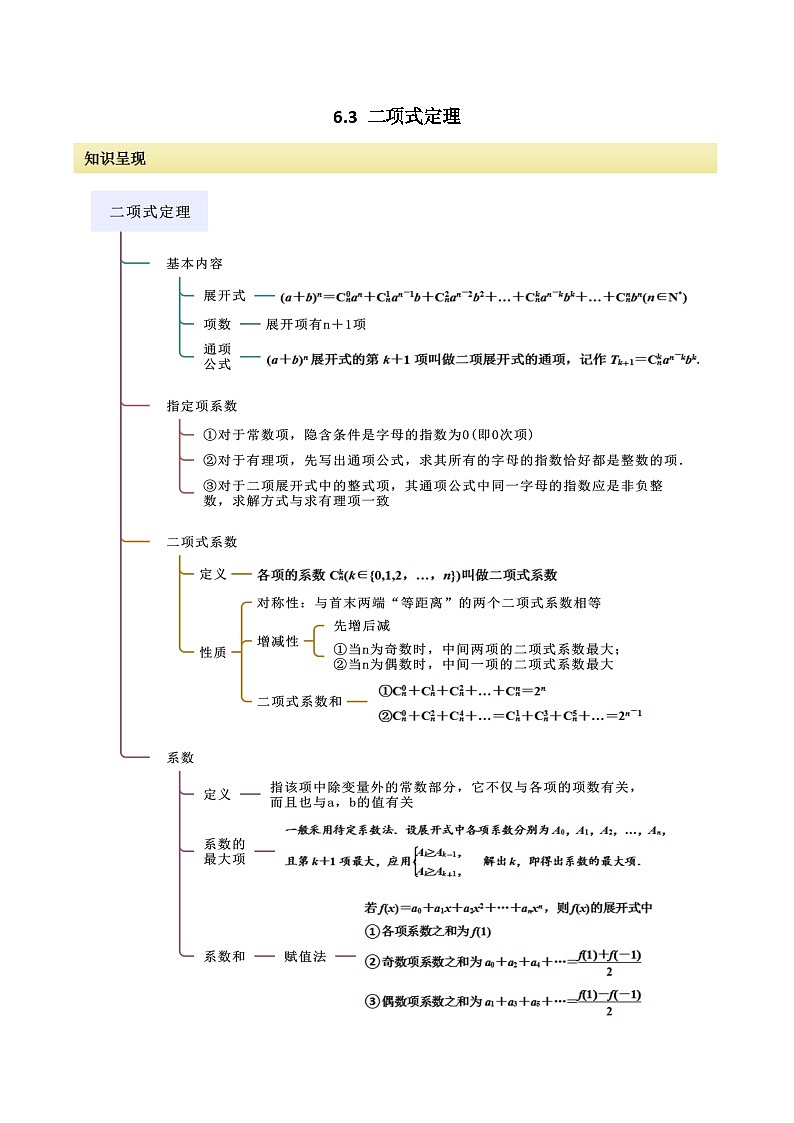

高中人教A版 (2019)第六章 计数原理6.3 二项式定理优秀同步测试题
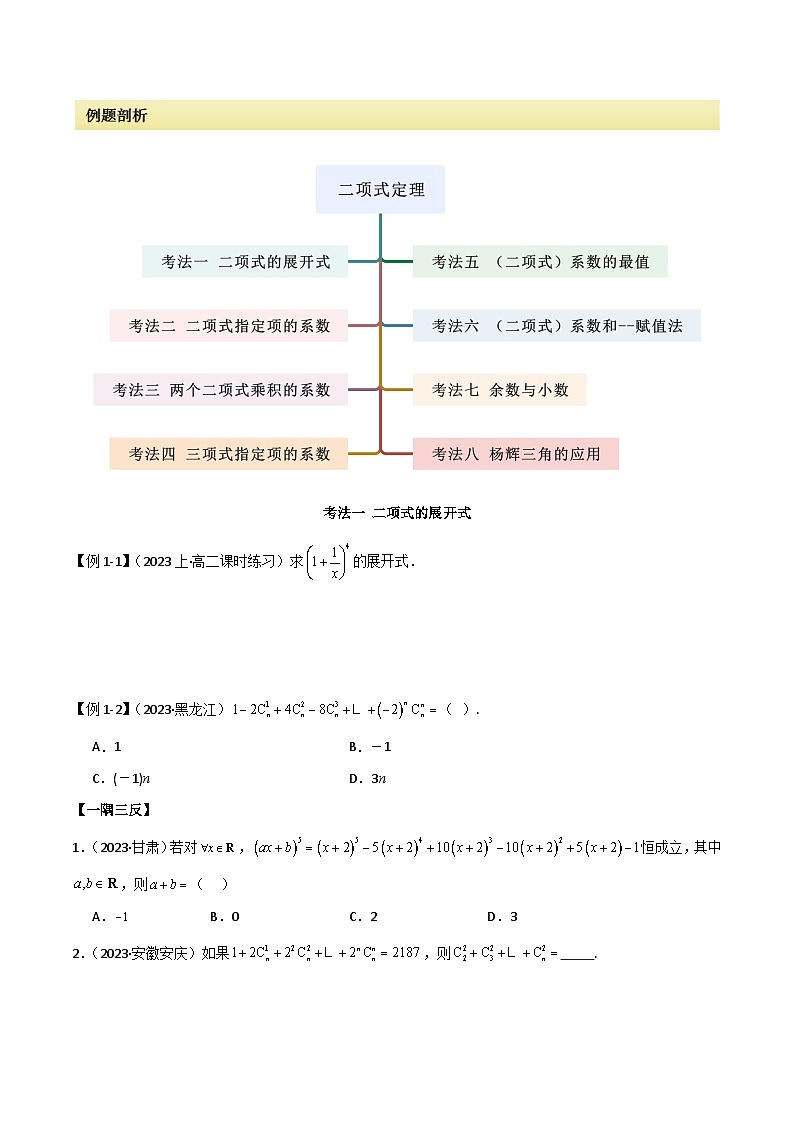
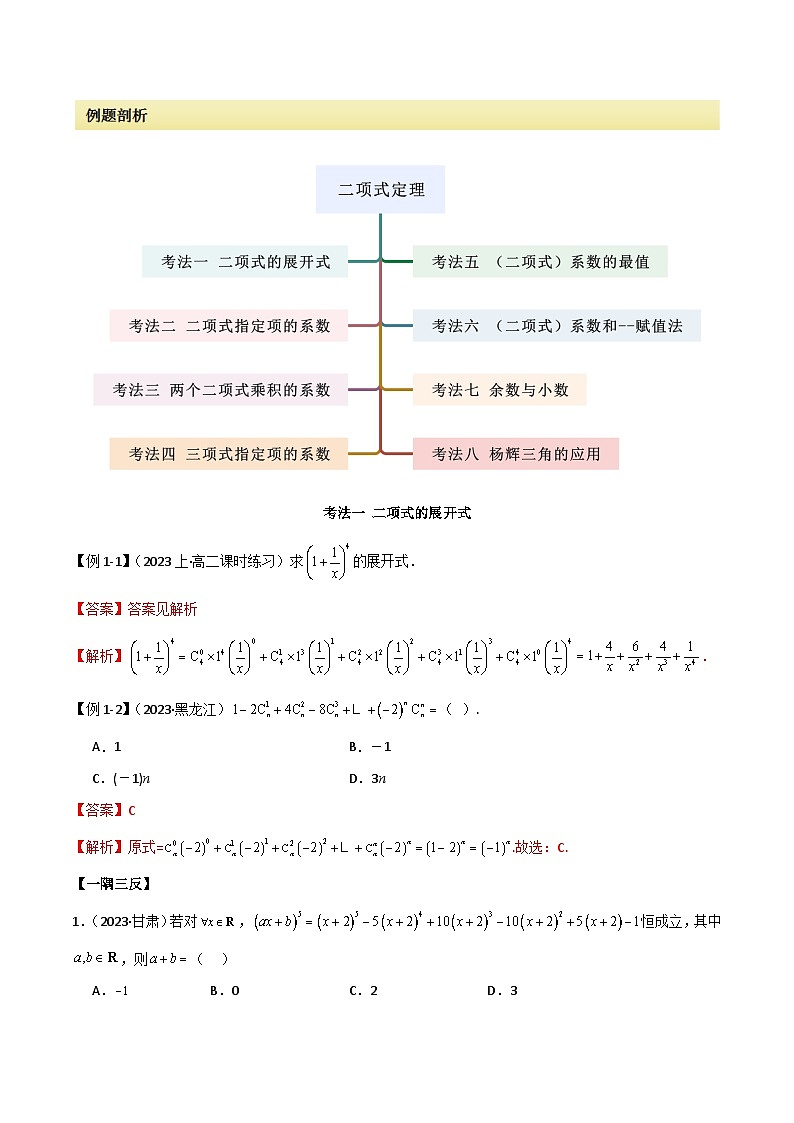
展开考法一 二项式的展开式
【例1-1】(2023上·高二课时练习)求的展开式.
【答案】答案见解析
【解析】.
【例1-2】(2023·黑龙江)( ).
A.1B.-1
C.(-1)nD.3n
【答案】C
【解析】原式=.故选:C.
【一隅三反】
1.(2023·甘肃)若对,恒成立,其中,则( )
A.B.0C.2D.3
【答案】C
【解析】由,
得,所以,.故选:C.
2.(2023·安徽安庆)如果,则 .
【答案】
【解析】依题意,
,解得,
.
故答案为:
(2023·高二课时练习)(1)求的展开式
(2)求的展开式;
(3)化简.
【答案】(1)(2)答案见解析;(3)
【解析】(1)
.
(2)
.
(3)原式
.
考法二 二项式指定项的系数
【例2-1】(2024·四川绵阳)的展开式中,x的系数为( )
A.B.C.5D.10
【答案】A
【解析】的展开式的通项为.
令,得.的系数为.故选:A.
【例2-2】.(2024·湖南)二项式的展开式中常数项为( )
A. B.C.D.
【答案】A
【解析】二项式的通项公式为,
令,所以常数项为,故选:A
【例2-3】(2024·云南)写出展开式中的一个有理项为 .
【答案】(答案不唯一)
【解析】展开式的通项公式为
所以展开式中的有理项分别为:时,;
时,;时,;时,.
故答案为:(四个有理项任写其一均可).
【一隅三反】
1.(2024·河南)展开式中的常数项为( )
A.672B.C.D.5376
【答案】D
【解析】二项式的展开式的通项,
令,得,所以二项展开式中的常数项为.故选:D
2.(2024安徽)展开式中含项的系数为,则实数a的值为( )
A.B.C.D.
【答案】A
【解析】,令,得.∴,
依题意,∴.故选:A.
3.(2023·全国·模拟预测)的展开式中,有理项是第 项.
【答案】3
【解析】的展开式的通项,其中,
当为有理项时,为整数,结合,所以,即有理项是展开式中的第3项,
故答案为:3
考法三 两个二项式乘积的系数
【例3-1】(2024·广东广州)在展开式中的系数为( )
A.B.0C.1D.2
【答案】B
【解析】显然,
则展开式第项,
当时,,当时,,
所以展开式中含的项为,即展开式中的系数为0.
故选:B
【例3-2】(2023·全国·模拟预测)的展开式中的系数为,则实数( )
A.2B.1C.D.
【答案】D
【解析】的展开式的通项公式为,所以.
令,解得,
.令,解得.
由题意,可知,所以.故选:D.
【一隅三反】
1.(2023·湖北)若的展开式中的的系数为,则实数( )
A.8B.7C.9D.10
【答案】B
【解析】由题意知,展开式的通项公式为,故的系数为,解得.故选:B.
2.(2024·广东·)的展开式中的系数为 .
【答案】
【解析】的展开式中的项为:,
所以展开式中的系数为.故答案为:
3.(2024·山东滨州)的展开式中的系数为 .(用数字作答)
【答案】
【解析】的通项公式为,
令得,,此时,
令得,,此时,
故的系数为故答案为:
考法四 三项式指定项的系数
【例4-1】(2023·全国·校联考模拟预测)在的展开式中常数项为( )
A.721B.-61C.181D.-59
【答案】D
【解析】=的展开式的通项公式为
=,
其中的展开式的通项公式为,
当时,,,常数项为;
当时,,,常数项为;
当时,,,常数项为;
故常数项为++.
故选:D
【例4-2】(2023·广东广州)的展开式中的系数为 (用数字作答).
【答案】
【解析】由于,所以的展开式中含的项为,所以的展开式中的系数为.
故答案为:
【一隅三反】
1(2023上·高二课时练习)的展开式中的系数为 .
【答案】92
【解析】,
又展开式的通项,
展开式的通项,
所以含的项为
则含的系数.
故答案为:.
2.(2024·福建)的展开式中,常数项为( )
A.B.C.70D.72
【答案】C
【解析】方法一:展开式中,
第项,
所以常数项为,
方法二:展开式中,
第项,
当时,展开式中常数项为;
当时,展开式中常数项为;
当时,,
所以的展开式中,常数项为70,
故选:C.
3.(2023上·河北唐山)的展开式中的系数为( )
A.208B.C.217D.
【答案】B
【解析】根据二项式定理可得,
的展开式中,含的项为.
所以,的展开式中的系数为.故选:B.
考法五 (二项式)系数的最值
【例5-1】(2023上·辽宁朝阳·高三建平县实验中学校联考阶段练习)在二项式的展开式中,二项式系数最大的是( )
A.第3项B.第4项
C.第5项D.第3项和第4项
【答案】B
【解析】二项式的展开式共有7项,则二项式系数最大的是第4项.故选:B.
【例5-2】(2023·四川雅安)的展开式中,系数最小的项是( )
A.第4项B.第5项C.第6项D.第7项
【答案】C
【解析】依题意,的展开通项公式为,其系数为,
当为奇数时,才能取得最小值,
又由二项式系数的性质可知,是的最大项,
所以当时,取得最小值,即第6项的系数最小.
故选:C.
【一隅三反】
1.(2022·重庆)(多选)若的展开式中第3项与第8项的系数相等,则展开式中二项式系数最大的项为( )
A.第4项B.第5项C.第6项D.第7项
【答案】BC
【解析】的展开式的通项为,因为展开式中第3项与第8项的系数相等,,所以,则展开式中二项式系数最大的项为第5项和第6项;故选:BC.
2.(2024·海南)在的二项展开式中,系数最大的项为和,则展开式中含项的系数为 .
【答案】7
【解析】,因为系数最大的项为和,所以为奇数,
,且,解得.所以含项的系数为.故答案为:7
3.(2023·上海嘉定)已知的二项展开式中系数最大的项为 .
【答案】
【解析】设系数最大的项为,则,解得,
因为且为整数,所以,此时最大的项为.故答案为:
4.(2023·上海)二项式的展开式中,系数最大的项为 .
【答案】
【解析】展开式通项公式为,且为整数.要想系数最大,则为偶数,
其中,,,,
显然系数最大项为.故答案为:
考法六 (二项式)系数和--赋值法
【例6-1】(2023·广东佛山)(多选)已知,则下列结论正确的是( )
A.
B.
C.
D.
【答案】ACD
【解析】对于A,令,则,故A正确;
对于B,因为,
所以,B错误;
对于C,令,则,
令,则 ,
所以,故C正确;
对于D,由选项B可知,,
,
所以
,故D正确.
故选:ACD.
【例6-2】(2023·广东佛山)(多选)若,其中为实数,则( )
A.B.
C.D.
【答案】AC
【解析】令可得,A正确.
,其展开式的第三项是,所以,B不正确.
令可得,所以,D不正确.
令可得,与相减可得,C正确.
故选:AC
【一隅三反】
1.(2023·河北)(多选)若,则( )
A.
B.
C.
D.
【答案】BD
【解析】对于A,当时,,A错误;
对于B,C,当时,,
当时,,
所以,,
所以B正确,C错误;
对于D,当时,,
所以,D正确.
故选:BD.
2.(2023·江苏扬州·高二统考期中)(多选)的展开式中第项和第项的二项式系数相等,则以下判断正确的是( )
A.第项的二项式系数最大B.所有奇数项二项式系数的和为
C.D.
【答案】AC
【解析】由题意,可得,所以,
对于A中,根据二项式定理的性质,可得中间项第项的二项式系数最大,所以A正确;
对于B中,根据二项式系数的性质,可得所有奇数项二项式系数的和为,所以B错误;
对于C中,对于C中,令,可得,
令,可得,所以,所以C正确;
对于D中,由,
可得,
即,
令,可得,所以D错误.
故选:AC.
3.(2024·黑龙江·高二校联考期末)(多选)若,其中为实数,则( )
A.B.
C.D.
【答案】AC
【解析】令,则原式转化为,
对A,令,得,故A正确;
对B,由二项式定理得,故B错误;
对CD,令,得,令,得,
所以,
所以,故C正确,D错误.
故选:AC
考法七 余数与小数
【例7-1】(2023下·河南郑州·高二校联考期中)除以所得的余数是 .
【答案】22
【解析】法一:由,前9项可以被整除,
而,故余数为.
法二:由,
而,故余数为.故答案为:
【例7-2】.(2023·高二课时练习)将精确到0.01的近似值是 .
【答案】0.96
【解析】因为,
且将精确到0.01,故近似值为0.96故答案为:0.96
【一隅三反】
1.(2023安徽)1.028的近似值是 .(精确到小数点后三位)
【答案】1.172
【解析】由题意得:.
故答案为:1.172
2.(2023上·河北)除以1000的余数是 .
【答案】24
【解析】因为
,
所以除以1000的余数是:.
故答案为:24
3.(2023下·江苏淮安·高二江苏省郑梁梅高级中学校考阶段练习)今天是星期日,经过7天后还是星期日,那么经过天后是( )
A.星期日B.星期一C.星期三D.星期四
【答案】B
【解析】,
因为能被整除,所以除以余,
所以经过天后是星期一.故选:B.
4.(2024·甘肃武威)干支纪年是中国古代的一种纪年法.分别排出十天干与十二地支如下:
天干:甲 乙 丙 丁 戊 己 庚 辛 壬 癸
地支:子 丑 寅 卯 辰 巳 午 未 申 酉 戌 亥
把天干与地支按以下方法依次配对:把第一个天干“甲”与第一个地支“子”配出“甲子”,把第二个天干“乙”与第二个地支“丑”配出“乙丑”,,若天干用完,则再从第一个天干开始循环使用.已知2023年是癸卯年,则年以后是 年.
【答案】丙午
【解析】因为,
所以年以后地支为“午”.
因为,
又因为除以10余数为3,所以年以后天干为“丙”,
故年以后是丙午年.
故答案为:丙午
考法八 杨辉三角的应用
【例8】(2023·广东广州)(多选)我国南宋数学家杨辉在年所著的《详解九章算法》一书里出现了如图所示的表,即杨辉三角,这是数学史上的一个伟大成就.该表蕴含着许多的数学规律,下列结论正确的是( )
第0行 1
第1行 1 1
第2行 1 2 1
第3行 1 3 3 1
第4行 1 4 6 4 1
第5行 1 5 10 10 5 1
第6行 1 6 15 20 15 6 1
…… ……
A.
B.,,,
C.从左往右逐行数,第项在第行第个
D.第行到第行的所有数字之和为
【答案】AC
【解析】对于A选项,由组合数的计算性质,
所以,
,A对;
对于B选项,
,B错;
对于C选项,第行共有项,
从左往右逐行数,第行最后一项对应的项数为,
因为,且,
所以,从左往右逐行数,第项在第行第个,C对;
对于D选项,第行所有项之和为,
所以,第行到第行的所有数字之和为,D错.
故选:AC.
【一隅三反】
1.(2023·山东青岛·高二校联考期中)(多选)我国南宋数学家杨辉1261年所著的《详解九章算法》一书中展示了二项式系数表,数学爱好者对杨辉三角做了广泛的研究.则下列结论正确的是( )
A.
B.第2023行的第1012个和第1013个数最大
C.第6行、第7行、第8行的第7个数之和为第9行的第7个数
D.第34行中从左到右第14个数与第15个数之比为2:3
【答案】ABD
【解析】A选项,,,故A正确;
B选项,由图可知:第行有个数字,如果是奇数,则第和第个数字最大,且这两个数字一样大;如果是偶数,则第个数字最大,故第2023行的第1012个和第1013个数最大,故B正确;
C选项,第6行,第7行,第8行的第7个数字分别为:1,7,28,其和为36;第9行第7个数字是84,故C错误;
D选项,依题意:第34行第14个数字是,第34行第15个数字是,所以,故D正确.
故选:ABD.
2.(2024上·江西·高二校联考期末)杨辉三角(如下图所示)是数学史上的一个伟大成就,杨辉三角中从第2行到第2023行,每行的第3个数字之和为( )
A.B.C.D.
【答案】B
【解析】
,
由题意可得,第2行到第2023行,每行的第3个数字之和为
,
故选:B.
3.(2023上·湖北 )如图,“杨辉三角”是二项式系数在三角形中的一种几何排列,在我国南宋数学家杨辉1261年所著的《详解九章算法》一书中出现,比欧洲发现早500年左右.现从杨辉三角第20行随机取一个数,该数大于2023的概率为( )
A.B.C.D.
【答案】A
【解析】由杨辉三角的性质知第20行的数为,一共有21个数,
其中,
由杨辉三角的对称性可知,第20行中大于2023的数的个数为,
故所求概率为.
故选:A.
单选题
1.(2023·四川南充)二项式的展开式中常数项为( )
A.B.60C.210D.
【答案】B
【解析】展开式的通项为,所以,
常数项为,故选:B.
2.(2023·河北)若,则( )
A.1B.0C.D.
【答案】C
【解析】,
当且时,,
因此,.故选:C.
3.(2024上海)二项式的展开式中,其中是有理项的项数共有( )
A.4项B.7项C.5项D.6项
【答案】D
【解析】二项式的展开式中,通项公式为,
,时满足题意,共6项.故选:D.
4.(2023安徽省)在的展开式中,只有第5项的二项式系数最大,则展开式中的系数为( )
A.B.C.D.7
【答案】D
【解析】因为在的展开式中,只有第5项的二项式系数最大所以所以的展开式的通项令,得
所以展开式中的系数为故选:D
5.(2023安徽)展开式中的系数为( )
A.15B.20C.30D.35
【答案】D
【解析】因为展开式的通项为,所以展开式中含的项为和.
因为,所以展开式中的系数为35.故选:D
6.(2023下·四川达州·高二统考期末)的展开式中,的系数为( )
A.20B.C.D.15
【答案】B
【解析】,其展开式的通项为:,
取得到的系数为.故选:B.
7.(2023云南)在的二项展开式中,系数最大的是第( )项
A.3B.4C.5D.6
【答案】C
【解析】在二项式的展开式中,通项公式为,
故第r+1项的系数为 ,当时,系数为正,
因为,所以当r=4时,系数最大的项是第5项.故选:C
8.(2023·江西赣州·)在的展开式中,下列说法不正确的是( )
A.不存在常数项B.所有二项式系数的和为32
C.第3项和第4项二项式系数最大D.所有项的系数和为1
【答案】D
【分析】根据给定的二项式,写出展开式判断A;利用二项式性质判断BC;利用赋值法计算判断D作答.
【详解】
,因此在的展开式中没有常数项,A正确;
的展开式的所有二项式系数的和为,B正确;
的展开式的第3项和第4项二项式系数相等,并且最大,C正确;
当时,的展开式的所有项的系数和为,D错误.故选:D
多选题
9.(2024·辽宁辽阳)若展开式的二项式系数之和为64,则下列结论正确的是( )
A.该展开式中共有6项B.各项系数之和为1
C.常数项为D.只有第4项的二项式系数最大
【答案】BD
【解析】因为二项式系数之和为64,即有,所以,
则该展开式中共有7项,A错误;
令,得该展开式的各项系数之和为1,B正确;
通项,
令,得,,C错误;
二项式系数最大的是,它是第4项的二项式系数,D正确.
故选:BD.
10.(2023·辽宁朝阳)已知2,n,8成等差数列,则在的展开式中,下列说法正确的是( )
A.二项式系数之和为32B.各项系数之和为1
C.常数项为40D.展开式中系数最大的项为80x
【答案】ABD
【解析】由题意可得:,则,
对于选项A:二项式系数之和为,故A正确;
对于选项B:令,可得各项系数之和为,故B正确;
对于选项C、D:因为的展开式的通项公式为:
,
所以,
展开式中没有常数项,故C错误;
展开式中系数最大的项为80x,故D正确;
故选:ABD.
11.(2022上·辽宁本溪·高二校考期末)若,则( )
A.B.
C.D.
【答案】AD
【解析】由题意,当,,当时,,A正确;
当时,,
所以,,B,C错误;
,
当时,,
所以,D正确.
故选:AD.
12.(2023下·河北沧州·高二统考期中)已知,则( )
A.B.
C.D.
【答案】ACD
【解析】因为,
令可得,
令可得①,
所以,故A正确;
令可得②,
①②得,故B错误;
①②得,
又展开式的通项为(且),
所以当为奇数时展开式系数为负数,当为偶数时展开式系数为正数,
即,,
所以
,故C正确;
将两边对求导可得:
,
再令可得,故D正确;
故选:ACD
填空题
13.(2023下·安徽合肥·高二统考期末)已知,则的值为 .
【答案】
【解析】由,
可得
则,即,解得.
故答案为:.
14.(2023下·山西吕梁·高二统考阶段练习)被4除的余数为 .
【答案】1
【解析】因为,且2024可以被4整除,所以余数为1.故答案为:1.
15.(2023·北京)的展开式中常数项为 .(用数字作答)
【答案】
【解析】的展开式的通项(,1,2,…,8).
当时,其展开式的常数项为;
当时,其展开式中的系数为,
则的展开式中常数项为.
故答案为:
16.(2023上·山东·高二校联考阶段练习)展开式中各项的系数可以仿照杨辉三角构造如图所示的广义杨辉三角,其性质是以下各行每个数是它正上方和左、右两边三个数的和(不足3个数时,用0补上),则的展开式中,项的系数为 .
【答案】
【解析】根据题意,可得广义杨辉三角如图所示,
可知的展开式中,项的系数为项的系数为30,
所以的展开式中,项的系数为.故答案为:
解答题
17.(2023·广东梅州)在二项式的展开式中,求:
(1)二项式系数之和;
(2)各项系数之和;
(3)所有偶数项系数之和;
(4)系数绝对值之和.
【答案】(1)
(2)
(3)
(4)
【解析】(1)设
二项式系数之和为
(2)设,
则各项系数之和为,
令得
(3)由(2)知令可得:
将两式相减,可得:,
故所有偶数项系数之和为.
(4)方法一:
令则
方法二:即为 展开式中各项系数和,
令得
故系数绝对值之和为.
18.(2023·全国·高二随堂练习)(1)求的展开式中的常数项;
(2)若的展开式中的系数为,求a的值;
(3)求的展开式中的常数项;
(4)若的展开式中各项系数之和为128,求展开式中的系数.
【答案】答案见详解
【解析】(1)设的展开式通项为: ,
则,
当时,;
故的展开式中的常数项为672;
(2)设的展开式通项为: ,
则,
当时,结合题意知此时;
故a的值为2;
(3)设的展开式通项分别为: ,
则,
当时,,
当时,,
当时,
故的展开式中的常数项为;
(4)令,则由题意可知,
设的展开式通项为,则,
当时,,故展开式中的系数为21.
19.(2023上·四川攀枝花·高二统考期末)从①第4项的系数与第2项的系数之比是;②第3项与倒数第2项的二项式系数之和为36;这两个条件中任选一个,再解决补充完整的题目.
已知(),且的二项展开式中,____.
(1)求的值;
(2)①求二项展开式的中间项;
②求的值.
【答案】(1)条件选择见解析,
(2)①;②.
【解析】(1)若选择①第4项的系数与第2项的系数之比是,
则有,
化简可得,求得或(舍去).
若选择②第3项与倒数第2项的二项式系数之和为36,
则有,
化简可得,求得或(舍去).
(2)由(1)可得,
①的二项展开式的中间项为.
②二项式展开式的通项公式为,
所以、、、、为正数,、、、为负数.
在中,令.
再令,可得,
∴.
20.(2023下·江苏宿迁·高二统考期中)在的展开式中,把叫做三项式的次系数列.
(1)求的值;
(2)根据二项式定理,将等式的两边分别展开,可得左右两边的系数对应相等,如,利用上述思想方法,求的值.
【答案】(1)14
(2)0
【解析】(1)
令得: ①
令得: ②
①+②得:,
所以.
(2)因为
所以,
右边展开式中含项的系数为
,
而展开式中左边含项的系数为0,
所以.
21.(2023北京)在中,把叫做三项式系数.
(1)当时,写出三项式系数的值;
(2)的展开式中,二项式系数可用杨辉三角表示,如图:
第1行 1 1
第2行 1 2 1
第3行 1 3 3 1
第4行 1 4 6 4 1
第5行 1 5 10 10 5 1
…… ……
当,时,类比杨辉三角,请列出三项式系数表;
(3)求的值(可用组合数作答).
【答案】(1),,,,;(2)系数表见解析;(3).
【解析】(1)因为,所以,,,,.
(2)当,时,三项式系数表如下:
第1行 1 1 1
第2行 1 2 3 2 1
第3行 1 3 6 7 6 3 1
第4行 1 4 10 16 19 16 10 4 1
(3)
,
其中含项的系数为,
又,的展开式中的第项为,
令,解得,
所以含项的系数为;
所以.
22.(2023上·上海松江·高二上海市松江二中校考阶段练习)已知函数,,满足:①对任意,都有;②对任意都有.
(1)试证明:为上的严格增函数;
(2)求;
(3)令,,试证明:.
【答案】(1)证明见解析
(2)66
(3)证明见解析
【解析】(1)由①可知:对任意,,
整理得,
不妨设,则,从而,
所以函数为上的单调增函数.
(2)令,则,显然,否则,与矛盾.
从而,而由,即得.
又由(1)知,即.
于是得,且,从而,即.
由知.
于是,
,,
,,
, 由于,
而且由(1)知,函数为单调增函数,因此.
从而.
(3),
,.
即数列是以为首项,以为公比的等比数列.
∴
于是,显然,
另一方面,
从而.
综上所述,.
人教A版 (2019)选择性必修 第三册8.2 一元线性回归模型及其应用同步测试题: 这是一份人教A版 (2019)选择性必修 第三册<a href="/sx/tb_c4000364_t7/?tag_id=28" target="_blank">8.2 一元线性回归模型及其应用同步测试题</a>,文件包含人教版高中数学选择性必修三精讲精练82一元线性回归模型及应用原卷版docx、人教版高中数学选择性必修三精讲精练82一元线性回归模型及应用解析版docx等2份试卷配套教学资源,其中试卷共58页, 欢迎下载使用。
人教A版 (2019)选择性必修 第三册8.1 成对数据的相关关系课后测评: 这是一份人教A版 (2019)选择性必修 第三册<a href="/sx/tb_c4000363_t7/?tag_id=28" target="_blank">8.1 成对数据的相关关系课后测评</a>,文件包含人教版高中数学选择性必修三精讲精练81成对数据的统计相关性原卷版docx、人教版高中数学选择性必修三精讲精练81成对数据的统计相关性解析版docx等2份试卷配套教学资源,其中试卷共45页, 欢迎下载使用。
高中数学人教A版 (2019)选择性必修 第三册第七章 随机变量及其分布7.2 离散型随机变量及其分布列课时作业: 这是一份高中数学人教A版 (2019)选择性必修 第三册<a href="/sx/tb_c4000357_t7/?tag_id=28" target="_blank">第七章 随机变量及其分布7.2 离散型随机变量及其分布列课时作业</a>,文件包含人教版高中数学选择性必修三精讲精练72离散型随机变量及分布列原卷版docx、人教版高中数学选择性必修三精讲精练72离散型随机变量及分布列解析版docx等2份试卷配套教学资源,其中试卷共37页, 欢迎下载使用。













