高中数学人教A版 (2019)必修 第二册第八章 立体几何初步8.6 空间直线、平面的垂直课时训练

这是一份高中数学人教A版 (2019)必修 第二册第八章 立体几何初步8.6 空间直线、平面的垂直课时训练，文件包含人教版高中数学必修二精讲精练862空间距离与空间角原卷版docx、人教版高中数学必修二精讲精练862空间距离与空间角解析版docx等2份试卷配套教学资源，其中试卷共67页， 欢迎下载使用。


考法一 线面角
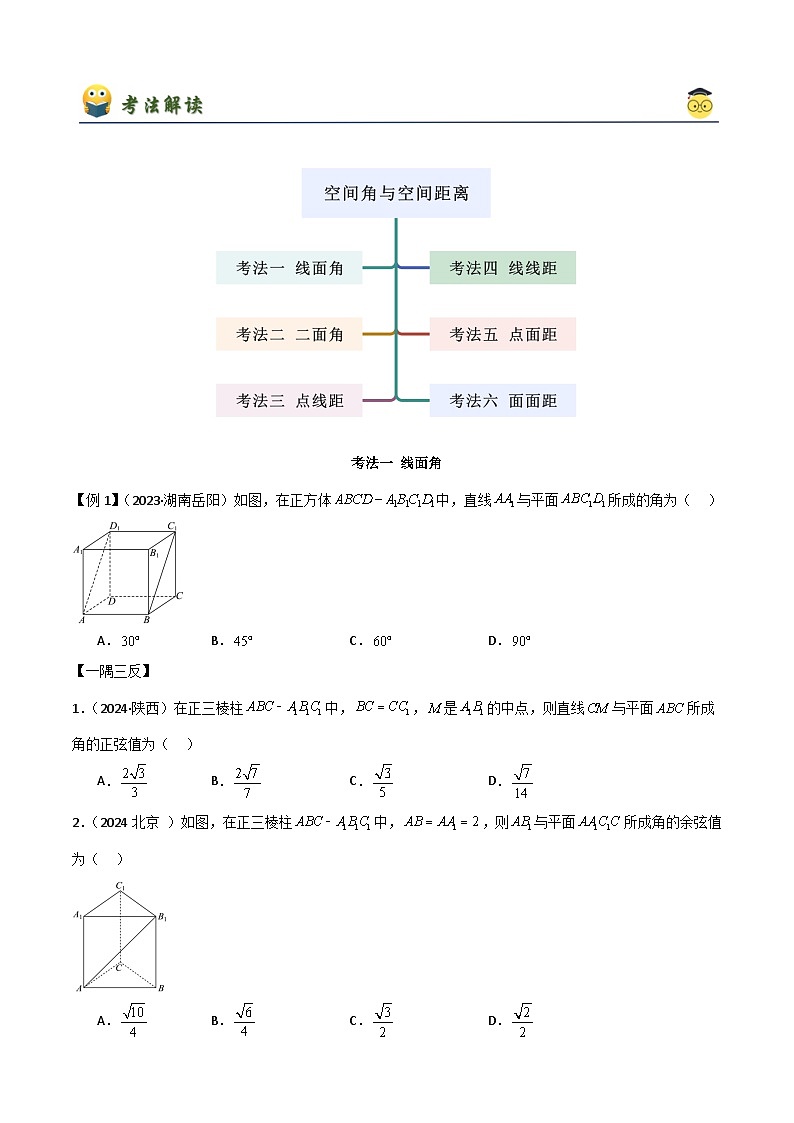
【例1】（2023·湖南岳阳）如图，在正方体中，直线与平面所成的角为（ ）
A．B．C．D．
【一隅三反】
1．（2024·陕西）在正三棱柱中，，是的中点，则直线与平面所成角的正弦值为（ ）
A．B．C．D．
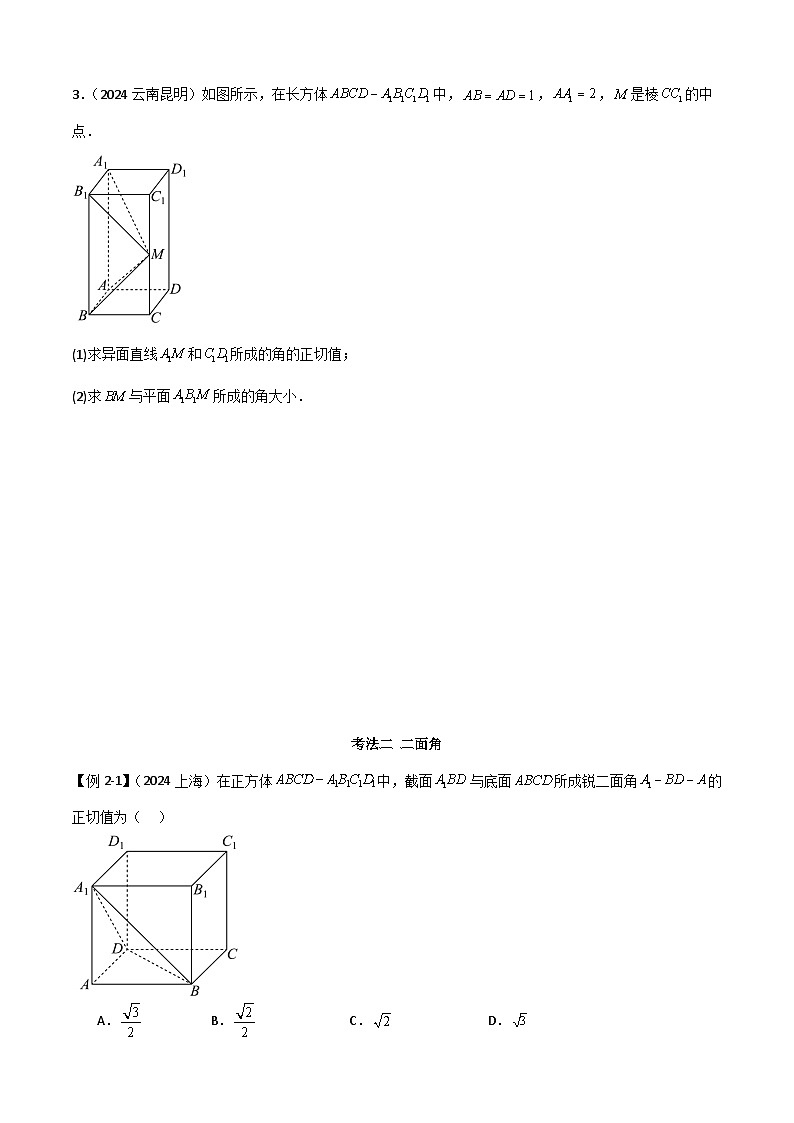
2．（2024北京 ）如图，在正三棱柱中，，则与平面所成角的余弦值为（ ）
A．B．C．D．
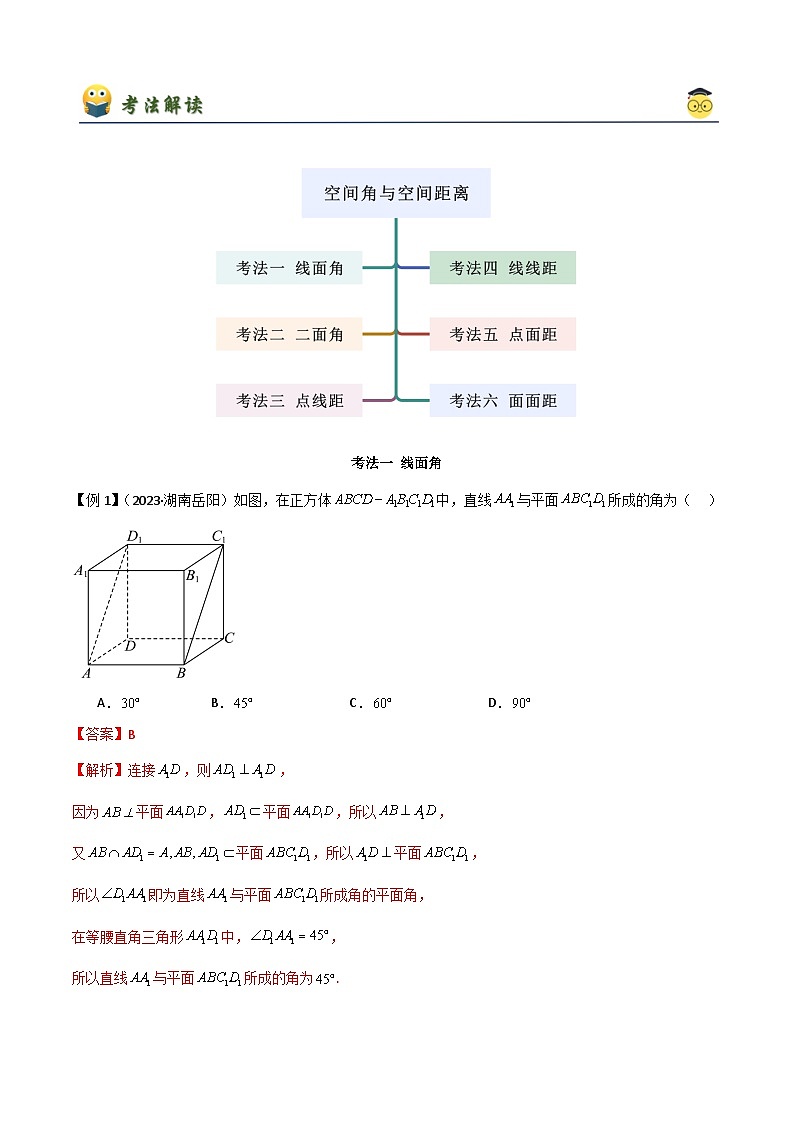
3．（2024云南昆明）如图所示，在长方体中，，，是棱的中点．
(1)求异面直线和所成的角的正切值；
(2)求与平面所成的角大小．
考法二 二面角
【例2-1】（2024上海）在正方体中，截面与底面所成锐二面角的正切值为（ ）
A．B．C．D．
【例2-2】（2024广东广州）如图1，在矩形ABCD中，，．将△BCD沿BD翻折至，且，如图2．

(1)求证：平面平面；
(2)求平面与平面ABD夹角的余弦值．
【一隅三反】
1．（2024安徽合肥）如图，三棱锥中，且为正三角形，分别是的中点，若截面侧面，则此棱锥侧面与底面夹角的余弦值为 .
2．（2024天津和平）如图，正方体，棱长为是的中点，则二面角的正弦值为（ ）

A．B．C．D．
3．（2023·四川）如图所示，是正三角形，平面，，，，且F为的中点.
(1)求证：平面；
(2)求平面与平面所成二面角的正弦值.
考法三 点线距
【例3】（2024湖北）已知垂直于所在的平面，，则点到的距离为 ．
【一隅三反】
1．（2023重庆·期中）如图在棱长为2的正方体，中E为BC的中点，点P在线段上，点P到直线的距离的最小值为（ ）

A．B．C．D．
2．（2023上海·期末）为直角梯形，，，，平面，，
(1)求证：；
(2)求点到直线的距离.
考法四 线线距
【例4】（2024江苏）如图，在正方体中，棱长为1，写出下列异面直线的公垂线并求异面直线的距离．
(1)和；
(2)和；
(3)和．
【一隅三反】
1．（2024上海普陀）在四面体中，若，则异面直线与的距离为 ．
2．（2024河北）如图，已知四棱锥中，为矩形，平面，，异面直线与之间的距离为 .
3．（2024江苏）在棱长为1的正方体中，直线AC与直线的距离是 ．
考法五 点面距
【例5】（2023新疆喀什·期末）如图，在四棱锥中，平面，，.
(1)求证：平面；
(2)若，求点C到平面的距离.
【一隅三反】
1．（2023北京）如图，正方形的边长为分别是的中点，将沿折起，使得为正三角形．
(1)求证：平面；
(2)求点到平面的距离．
2．（2024湖南）如图，在四棱锥中，平面，，，，为线段的中点，PB与底面ABCD所成角正切值为．

(1)求证：；
(2)求点D到面的距离．
3（2024四川雅安）如图，在四棱柱中，底面和侧面均是边长为2的正方形．
(1)证明：．
(2)若，求点到平面的距离．
考法六 面面距
【例6】（2023·河南）如图所示，正六棱柱的底面边长为1，高为.

(1)证明：平面平面；
(2)求平面与平面间的距离.
【一隅三反】
1．（2023福建）在长方体中，有一过且与平面平行的平面，棱，，则平面与平面的距离是 ．
2．（2024北京）直四棱柱中，底面为正方形，边长为，侧棱，分别为的中点，分别是的中点．

(1)求证：平面平面；
(2)求平面与平面的距离．
3（2024江西）如图，在棱长为a的正方体ABCD－A1B1C1D1中，E、F分别是AA1与CC1的中点.
(1)证明：平面EB1D1平面FBD；
(2)求平面EB1D1与平面FBD之间的距离.
单选题
1．（2024山东）已知正四棱台的上、下底面边长分别为2和4，若侧棱与底面ABCD所成的角为，则该正四棱台的体积为（ ）
A．B．C．D．
2．（2023山东）在底面为正方形，侧棱垂直于底面的四棱柱中，，异面直线与所成角的余弦值为，则直线与直线的距离为（ ）
A．2B．1C．D．
3．（2024湖北）在直三棱柱中，所有棱长均为1，则点到平面的距离为（ ）
A．B．C．D．
4．（2024河北 ）已知正方体的棱长为为线段上的动点，则点到平面距离的最小值为（ ）
A．1B．C．D．2
5．（2024湖北宜昌 ）在棱长为的正方体中，，分别为棱，的中点， 则点到平面的距离为（ ）
A．B．
C．D．
6．（2024广东汕头 ）如图，在三棱锥中，平面，则下列选项中，不正确的是（ ）
A．平面平面
B．二面角的余弦值为
C．与平面所成角为
D．三棱锥外接球的表面积为
7．（2023·全国·模拟预测）在长方体中，已知与所成的角为，与平面所成的角为，则下列结论错误的是（ ）
A．B．与平面所成的角为
C．平面D．与平面所成的角为
8．（2024陕西咸阳）如图，边长为2的两个等边三角形，若点到平面的距离为，则二面角的大小为（ ）

A．B．C．D．
多选题
9．（2024山东）在正方体中，下列结论正确的是（ ）．
A．B．平面
C．直线与所成的角为D．二面角的大小为
10．（2024黑龙江）如图，正方体的棱长为1，则下列四个命题正确的是（ ）

A．两条异面直线和所成的角为
B．直线与平面垂直
C．点到面的距离为
D．三棱柱外接球表面积为
11．（2023福建漳州 ）如图，三棱锥中，，平面，则下列结论正确的是（ ）
A．直线与平面所成的角为
B．二面角的正切值为
C．点到平面的距离为
D．
12．（2024山东 ）在如图所示的三棱锥中，，面，，下列结论正确的为（ ）
A．直线与平面所成的角为
B．二面角的正切值为
C．到面的距离为
D．异面直线
填空题
13．（2024上海）已知正方体的棱长为1，则异面直线与之间的距离是 .
14．（2023上海·期末）如图所示，正四面体的棱长为1，则点到平面的距离为 .
15．（2024河北）在正方体中，与平面所成角的大小为 .
16．（2023北京）在正三棱柱中，，则直线到平面的距离为
解答题
17．（2024·四川）如图，在四棱锥中，，，平面平面．
(1)证明：平面；
(2)已知，且，求点D到平面的距离．
18（2024陕西）如图，在四棱锥中，底面为平行四边形，是与的交点，，平面是的中点．
(1)证明：平面；
(2)求直线与平面所成角的正切值．
19．（2023甘肃）如图，在三棱台中，平面，，，.
(1)求证：平面平面；
(2)求与平面所成角正弦值.
20．（2024江苏苏州·阶段练习）在三棱台中，，，且平面平面．
(1)求证：平面平面；
(2)求二面角的正弦值．
21（2024河北）在平行六面体中，已知，．
(1)证明：平面；
(2)当三棱锥体积最大时，求二面角的余弦值．
22．（2024湖南）如图，平行六面体的底面是菱形，且．试用尽可能多的方法解决以下两问：

(1)若，记面为，面为，求二面角的平面角的余弦值；
(2)当的值为多少时，能使平面？