





还剩30页未读,
继续阅读
所属成套资源:2024秋青岛版数学初三上学期课件PPT整册
成套系列资料,整套一键下载
青岛版数学九上第一章《图形的相似回顾与总结》课件
展开
这是一份青岛版数学九上第一章《图形的相似回顾与总结》课件,共38页。
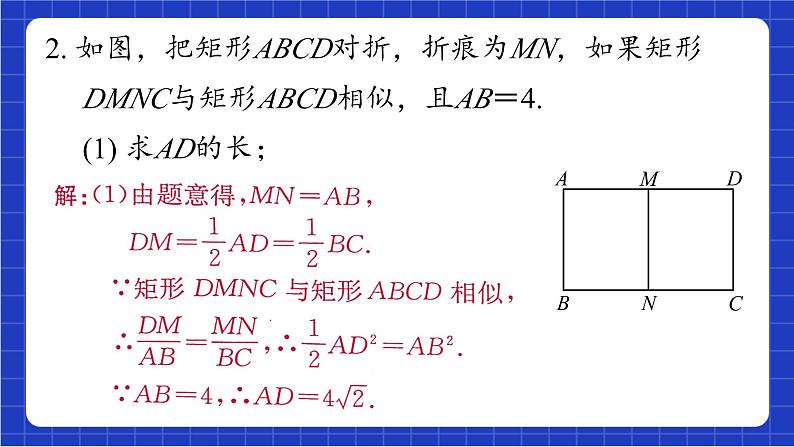
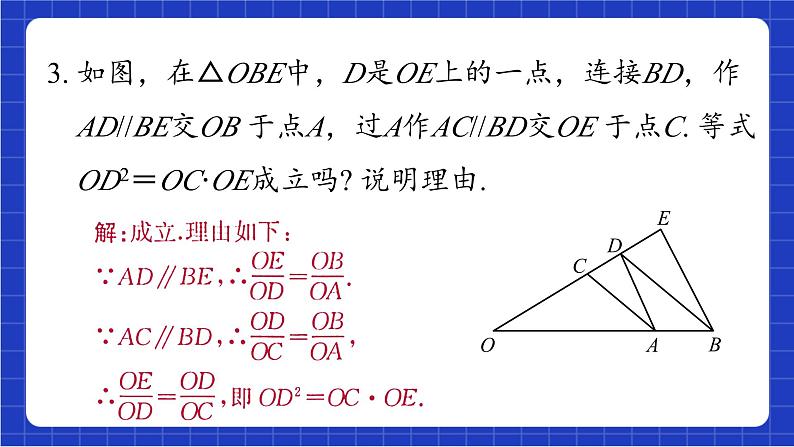
1.1相似多边形回顾与总结青岛版数学九年级上册1. 什么叫做相似形?什么叫做相似多边形? 全等形与相 似形有哪些联系与区别?2. 什么叫做两个相似多边形的相似比?3. 基本事实9及其推论是什么?4. 你学过哪几个相似三角形的判定定理?复习导入5. 你学过相似三角形的哪些性质?6. 全等三角形与相似三角形的性质与判定有哪些相同与 不同?7. 什么叫做位似图形? 怎样利用位似将图形放大或缩小?8. 你能举出现实生活中相似形和位似图形的应用实例吗?9. 在直角坐标系中,如果将一个多边形的顶点坐标(有 一个顶点为原点,有一条边在横轴上) 分别扩大或缩 小相同的倍数,所得到的图形与原图形有什么关系?1. 所有正方形都相似吗? 为什么?所有矩形都相似吗? 为什么?解:所有正方形都相似. 因为所有正方形的对应边成比例,对应角相等,所以所有的正方形都相似. 所有的矩形不一定都相似. 因为所有矩形的对应边不一定成比例.综合练习2. 如图,把矩形ABCD对折,折痕为MN,如果矩形 DMNC与矩形ABCD相似,且AB=4. (1) 求AD的长; (2) 求矩形DMNC与矩形ABCD的相似比. 3. 如图,在△OBE中,D是OE上的一点,连接BD,作 AD//BE交OB 于点A,过A作AC//BD交OE 于点C. 等式 OD2=OC·OE成立吗? 说明理由.4. 如图,△ABC∽△ACD. (1) 写出图中相等的角;解:∠B=∠ACD, ∠ACB=∠ADC.(2) 已知AD=4cm,AC=6cm,求AB的长.5. 如图,在△PAD中,∠APD=120°,B,C为AD上 的点,△PBC为等边三角形. 找出图中的相似三角形, 并说明理由.解:△ABP∽△PCD.6. 如图,点D在AB上,点E,F在AC上, AF∶AE=AD∶AB=AE∶AC. 图中有 哪些线段互相平行?请说明你的理由. B 9. 如图是小孔成像原理的示意图,如果物体AB的高度为 36 cm,根据图中标注的尺寸那么它在暗箱所成的像 CD的高度是多少厘米?10. 如果一个三角形的两边和其中一边上的中线,与另一 个三角形的两边和其中一边上的中线对应成比例. 这 两个三角形相似吗?为什么?11. 如图,在△ABC中,D为AB边上一点, △CBD ∽△ACD. (1) 求∠ADC及∠ACB的度数;(2) 如果AD=4,BD=9,求CD的长.12. 如图,在矩形ABCD中,E是边CD的中点,BF⊥AE, 垂足为点F. 设 AB=a,BC=b,求BF的长.13. 选择题:如图所示的直角坐标系中,y轴右边的小 “鱼”与y轴左边的大“鱼”是位似图形.如果小“鱼” 上的一个“顶点”的坐标为 (a,b).那么大“鱼”上对 应“顶点”的坐标是 ( ). (A) (-a,-2b) (B) (-2a,-b) (C) (-2a,-2b) (D) (-2b,-2a)C 14. 大刚在晚上由灯柱A走向灯柱 B. 当他走到P点时,发觉他身后影子的顶部刚好接触到灯柱A的底部. 当他向前再走20 m到达Q点时,发觉他身前影子的顶部刚好接触到灯柱B的底部. 已知大刚的身高是 1.7 m,两支灯柱的高度都是9.6m,设AP= x m.求两支灯柱之间的距离.DC 解:如图所示,由题意可知△BQC ∽ △BAD,DC 15. 如图,在Rt△BCA中,∠C=90°,AC=3,BC=4,过点C作CA1⊥AB,垂足为点A1,再过点A1作A1C1⊥BC,垂足为点 C1,······按以上的方法继续作下去,得到Rt△A5C5C4.(1) 图中与Rt△A5C5C4相似的三角形共有多少个?20个(2) 求线段A5C5的长.解:在 Rt△ABC 中, ∵AC=3,BC=4, ∴AB=5. 16. 如图,O为矩形ABCD的中心,将三角尺的直角顶点与点O重合,直角边分别与矩形的两边AB,BC分别相交于点N和M,当三角尺绕点O旋转时始终与AB,BC相交.如果AB=4,AD=6,OM=x,ON=y,试写出y与x的表达式. 解:如图所示,过点 O作OE⊥AB 于点E,过点 O作OF⊥BC 于点F.FEFE17. 如图是由 12 个有公共顶点O的直角三角形拼成的图 形,在这些三角形中,以O为顶点的角都等于30°. (1) 图中与△ABO相似的三角形有多少个?11个(2) 图中有没有与△ABO位似的三角形? 如果有,指出它是哪一个.有,△GHO. 18. 如图,图①是第17题图形的缩小图,它是由一些相似的直角三角形组成的“海螺”图案;图②是由一些相似的正五边形组成的“玫瑰花”图案;图③是由一些大小不等的圆 ( 所有的圆也可看作是相似形) 组成的“贝壳”图案. 请你也利用一些相似形设计几个美丽的图案,并加以命名;同时搜集几个用相似形构成的图案. 看谁设计得好,搜集得多.解:如图所示.(答案不唯一)课程结束
1.1相似多边形回顾与总结青岛版数学九年级上册1. 什么叫做相似形?什么叫做相似多边形? 全等形与相 似形有哪些联系与区别?2. 什么叫做两个相似多边形的相似比?3. 基本事实9及其推论是什么?4. 你学过哪几个相似三角形的判定定理?复习导入5. 你学过相似三角形的哪些性质?6. 全等三角形与相似三角形的性质与判定有哪些相同与 不同?7. 什么叫做位似图形? 怎样利用位似将图形放大或缩小?8. 你能举出现实生活中相似形和位似图形的应用实例吗?9. 在直角坐标系中,如果将一个多边形的顶点坐标(有 一个顶点为原点,有一条边在横轴上) 分别扩大或缩 小相同的倍数,所得到的图形与原图形有什么关系?1. 所有正方形都相似吗? 为什么?所有矩形都相似吗? 为什么?解:所有正方形都相似. 因为所有正方形的对应边成比例,对应角相等,所以所有的正方形都相似. 所有的矩形不一定都相似. 因为所有矩形的对应边不一定成比例.综合练习2. 如图,把矩形ABCD对折,折痕为MN,如果矩形 DMNC与矩形ABCD相似,且AB=4. (1) 求AD的长; (2) 求矩形DMNC与矩形ABCD的相似比. 3. 如图,在△OBE中,D是OE上的一点,连接BD,作 AD//BE交OB 于点A,过A作AC//BD交OE 于点C. 等式 OD2=OC·OE成立吗? 说明理由.4. 如图,△ABC∽△ACD. (1) 写出图中相等的角;解:∠B=∠ACD, ∠ACB=∠ADC.(2) 已知AD=4cm,AC=6cm,求AB的长.5. 如图,在△PAD中,∠APD=120°,B,C为AD上 的点,△PBC为等边三角形. 找出图中的相似三角形, 并说明理由.解:△ABP∽△PCD.6. 如图,点D在AB上,点E,F在AC上, AF∶AE=AD∶AB=AE∶AC. 图中有 哪些线段互相平行?请说明你的理由. B 9. 如图是小孔成像原理的示意图,如果物体AB的高度为 36 cm,根据图中标注的尺寸那么它在暗箱所成的像 CD的高度是多少厘米?10. 如果一个三角形的两边和其中一边上的中线,与另一 个三角形的两边和其中一边上的中线对应成比例. 这 两个三角形相似吗?为什么?11. 如图,在△ABC中,D为AB边上一点, △CBD ∽△ACD. (1) 求∠ADC及∠ACB的度数;(2) 如果AD=4,BD=9,求CD的长.12. 如图,在矩形ABCD中,E是边CD的中点,BF⊥AE, 垂足为点F. 设 AB=a,BC=b,求BF的长.13. 选择题:如图所示的直角坐标系中,y轴右边的小 “鱼”与y轴左边的大“鱼”是位似图形.如果小“鱼” 上的一个“顶点”的坐标为 (a,b).那么大“鱼”上对 应“顶点”的坐标是 ( ). (A) (-a,-2b) (B) (-2a,-b) (C) (-2a,-2b) (D) (-2b,-2a)C 14. 大刚在晚上由灯柱A走向灯柱 B. 当他走到P点时,发觉他身后影子的顶部刚好接触到灯柱A的底部. 当他向前再走20 m到达Q点时,发觉他身前影子的顶部刚好接触到灯柱B的底部. 已知大刚的身高是 1.7 m,两支灯柱的高度都是9.6m,设AP= x m.求两支灯柱之间的距离.DC 解:如图所示,由题意可知△BQC ∽ △BAD,DC 15. 如图,在Rt△BCA中,∠C=90°,AC=3,BC=4,过点C作CA1⊥AB,垂足为点A1,再过点A1作A1C1⊥BC,垂足为点 C1,······按以上的方法继续作下去,得到Rt△A5C5C4.(1) 图中与Rt△A5C5C4相似的三角形共有多少个?20个(2) 求线段A5C5的长.解:在 Rt△ABC 中, ∵AC=3,BC=4, ∴AB=5. 16. 如图,O为矩形ABCD的中心,将三角尺的直角顶点与点O重合,直角边分别与矩形的两边AB,BC分别相交于点N和M,当三角尺绕点O旋转时始终与AB,BC相交.如果AB=4,AD=6,OM=x,ON=y,试写出y与x的表达式. 解:如图所示,过点 O作OE⊥AB 于点E,过点 O作OF⊥BC 于点F.FEFE17. 如图是由 12 个有公共顶点O的直角三角形拼成的图 形,在这些三角形中,以O为顶点的角都等于30°. (1) 图中与△ABO相似的三角形有多少个?11个(2) 图中有没有与△ABO位似的三角形? 如果有,指出它是哪一个.有,△GHO. 18. 如图,图①是第17题图形的缩小图,它是由一些相似的直角三角形组成的“海螺”图案;图②是由一些相似的正五边形组成的“玫瑰花”图案;图③是由一些大小不等的圆 ( 所有的圆也可看作是相似形) 组成的“贝壳”图案. 请你也利用一些相似形设计几个美丽的图案,并加以命名;同时搜集几个用相似形构成的图案. 看谁设计得好,搜集得多.解:如图所示.(答案不唯一)课程结束
相关资料
更多









