2022年浙江省杭十高三数学11月月考理新人教A版会员独享

这是一份2022年浙江省杭十高三数学11月月考理新人教A版会员独享，共4页。试卷主要包含了考试时间，设，建立如图的空间坐标系，等内容，欢迎下载使用。


考生须知：
1．本试卷分第I卷（选择题）和第II卷（非选择题）两部分，满分150分．
2．考试时间：11月8日下午13:30~15:30．
3．所有答案必须写在答题纸上，写在试题卷上无效．
参考公式：
如果事件A，B互斥，那么棱柱的体积公式

如果事件A，B相互独立，那么其中表示棱柱的底面积，表示棱柱的高
棱锥的体积公式
如果事件A在一次试验中发生的概率
是p，那么次独立重复试验中事件A其中表示棱锥的底面积，表示棱锥的高
恰好发生k次的概率 棱台的体积公式
，h表示棱台的高
球的表面积公式 球的体积公式

其中S1、S2分别表示棱台的上、下底面积，表示球的半径
第Ⅰ卷（选择题 共50分）
一、选择题：本大题共10小题，每小题5分，共50分．在每小题给出的四个选项中，只有一项是符合题目要求的。
（1）若集合，，则
（A）（B）（C）（D）
（2）设（i为虚数单位），则
（A）（B）（C）（D）
（3）已知命题p：，使；命题q：，都有．给出下列结论：
①命题“”是真命题②命题“”是真命题
③命题“”是假命题④命题“”是假命题
其中正确的是
（A）②③（B）②④（C）③④（D）①②③
（4）已知，则“”是“”的
（A）充分不必要条件（B）必要不充分条件
（C）充要条件（D）既不充分也不必要条件
（5）等差数列的前n项和，若，，则等于
（A）152（B）154
（C）156（D）158
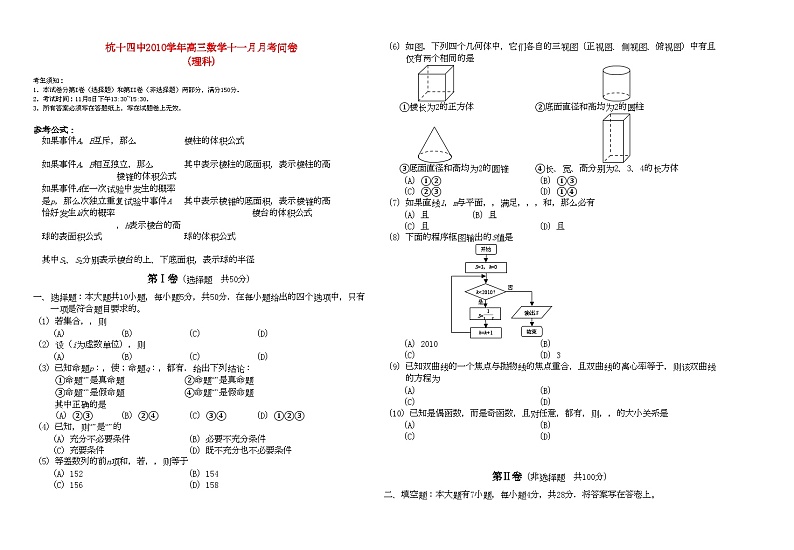
（6）如图，下列四个几何体中，它们各自的三视图（正视图、侧视图、俯视图）中有且仅有两个相同的是
①棱长为2的正方体②底面直径和高均为2的圆柱
③底面直径和高均为2的圆锥④长、宽、高分别为2、3、4的长方体
（A）①②（B）①③
（C）②③（D）①④
（7）如果直线l，m与平面，，满足，，，和，那么必有
（A）且（B）且
（C）且（D）且
（8）下面的程序框图输出的S值是
开始
S=3，k=0
S= EQ \f(1,1-S) eq\f(1,1-S)
k<2010?
结束
输出S
否
是
k=k+1
（A）2010（B）
（C）（D）3
（9）已知双曲线的一个焦点与抛物线的焦点重合，且双曲线的离心率等于，则该双曲线的方程为
（A）（B）
（C）（D）
（10）已知是偶函数，而是奇函数，且对任意，都有，则，，的大小关系是
（A）（B）
（C）（D）
第Ⅱ卷（非选择题 共100分）
二、填空题：本大题有7小题，每小题4分，共28分．将答案写在答卷上。
（11）若二项式的展开式中的常数项为，则= ．
（12）若不等式组所表示的平面区域被直线分成面积相等的两部分，则k的值为 ．
（13）从7盆不同的花中选出5盆摆放在主席台前，其中有两盆不许摆放在正中间，那么这里共有 种不同的摆法（用数字作答）．
（14）设点O在△ABC的外部，且，则 ．
（15）已知，，则 ．
（16）正整数按下列方法分组：
，，，，……，
记第n组中各数之和为；由自然数的立方构成下列数组：
，，，，……，
记第n组中后一个数与前一个数的差为，则 ．
（17）将正方形ABCD沿对角线BD折成直二面角，有如下四个结论：
①AC⊥BD；
②△ACD是等边三角形；
③AB与面BCD成60°角；
④AB与CD成60°角．
请你把正确的结论的序号都填上 ．
三、解答题：本大题共6小题，共72分，解答应写出文字说明，证明过程或或演算步骤。
（18）（本小题14分）
已知钝角△ABC中，角A、B、C的对边分别为a、b、c，且有
（Ⅰ）求角B的大小；
（Ⅱ）设向量，，且m⊥n，求的值．
（19）（本题满分14分）
如图，四棱锥P—ABCD的底面ABCD为一直角梯形，其中BA⊥AD，CD⊥AD，CD=AD=2AB，PA⊥底面ABCD，E是PC的中点．
（Ⅰ）求证：BE//平面PAD；
（Ⅱ）若BE⊥平面PCD。
（i）求异面直线PD与BC所成角的余弦值；
（ii）求二面角E—BD—C的余弦值．
C
D
A
B
P
E
20．（本小题满分14分）
某项考试按科目A、科目B依次进行，只有当科目A成绩合格时，才可以继续参加科目B的考试。每个科目只允许有一次补考机会，两个科目成绩均合格方可获得该项合格证书，现在某同学将要参加这项考试，已知他每次考科目A成绩合格的概率均为，每次考科目B成绩合格的概率均为。假设他在这项考试中不放弃所有的考试机会，且每次的考试成绩互不影响，记他参加考试的次数为．
（Ⅰ）求的分布列和期望；
（Ⅱ）求该同学在这项考试中获得合格证书的概率．
（21）（本小题满分15分）
如图，已知椭圆=1（2≤m≤5），过其左焦点且斜率为1的直线与椭圆及直线的交点从左到右的顺序为A、B、C、D，设．
（Ⅰ）求的解析式；
（Ⅱ）求的最值．
A
B
C
D
O
x
y
（22）（本小题满分15分）
设关于x的方程有两个实根、，且．定义函数．
（Ⅰ）求的值；
（Ⅱ）判断在区间上的单调性，并加以证明；
（Ⅲ）若为正实数，证明不等式：．
参考答案
一、选择题CCBAC C BDDA
二、填空题
11．2 12． 13．1800 14． 15． 16．（15） 17．①②④
三、解答题
17．解：（Ⅰ），由正弦定理得：
…………………………………………………2分
即
…………………………………………………4分
因为在△ABC中则
…………………………………………………………7分
（Ⅱ）
即
即………………………………9分
由
………………………………………12分
则………………………………………14分
18．设，建立如图的空间坐标系，
，,
，．……………………………………2分
（Ⅰ），，
所以，
平面，平面． ……………………………………4分
（Ⅱ）平面，，即
，，即．…………………6分
①，
，
所以异面直线与所成角的余弦值为……………………………10分
②平面和平面中，，
所以平面的一个法向量为；
平面的一个法向量为；……………………………………12分
，所以二面角的余弦值为…………………14分
19．解：（Ⅰ）设该同学“第一次考科目A成绩合格”为事件A1，“科目A补考后成绩合格”为事件A2，“第一次考科目B成绩合格”为事件B1，“科目B补考后成绩合格”为事件B2 ．
由题意知，可能取得的值为：2，3，4…………2分

…………5分
的分布列为
故…………7分
（Ⅱ）设“该同学在这项考试中获得合格证书”为事件C
则

故该同学在这项考试中获得合格证书的概率为…………14分
21． 解 （Ⅰ）设椭圆的半长轴、半短轴及半焦距依次为a、b、c，则a2=m,b2=m－1,c2=a2－b2=1
∴椭圆的焦点为F1(－1,0),F2(1,0)
故直线的方程为y=x+1,又椭圆的准线方程为x=±,即x=±m
∴A(－m,－m+1),D(m,m+1)
考虑方程组,消去y得 (m－1)x2+m(x+1)2=m(m－1)
整理得 (2m－1)x2+2mx+2m－m2=0
Δ=4m2－4(2m－1)(2m－m2)=8m(m－1)2
∵2≤m≤5,∴Δ＞0恒成立，xB+xC=
又∵A、B、C、D都在直线y=x+1上
∴|AB|=|xB－xA|==(xB－xA)·,|CD|=(xD－xC)
∴||AB|－|CD||=|xB－xA+xD－xC|=|(xB+xC)－(xA+xD)|
又∵xA=－m,xD=m,∴xA+xD=0
∴||AB|－|CD||=|xB+xC|·=||·= (2≤m≤5)
故f(m)=，m∈［2,5］
（Ⅱ）由f(m)=，可知f(m)=
又2－≤2－≤2－，∴f(m)∈［］
故f(m)的最大值为，此时m=2;f(m)的最小值为，此时m=5
22． （Ⅰ）解：∵是方程的两个实根
∴
∴
同理
∴ …………5分
（Ⅱ）∵
∴ …………8分
当时，
而
∴在上为增函数 …………10分
（Ⅲ）∵且
∴

∴ …………12分
由（Ⅱ）可知
同理可得
∴
∴ …………14分
又由（Ⅰ）知
∴
所以 …………15分
2
3
4
P