




安徽省淮北市第二中学2024-2025学年九年级上学期期中检测数学试卷
展开
这是一份安徽省淮北市第二中学2024-2025学年九年级上学期期中检测数学试卷,文件包含安徽省淮北市第二中学2024-2025学年九年级上学期期中检测数学试卷解析docx、安徽省淮北市第二中学2024-2025学年九年级上学期期中检测数学试卷docx等2份试卷配套教学资源,其中试卷共28页, 欢迎下载使用。
一、选择题(本大题共10小题,每小题4分,满分40分.在每小题给出的A,B,C,D四个选项中,只有一个选项是符合题目要求的)
1.地图上淮北到合肥的距离为2.4厘米.比例尺是,那么淮北到合肥的实际距离是( )
A.2400米B.24000米C.240000米D.2400000米
2.若抛物线与的形状相同,则的值为( )
A.2B.3或C.1D.2或
3.如图,已知∠1=∠2,那么添加下列一个条件后,仍无法判定△ABC∽△ADE的是( )
A.B.C.D.
4.已知蓄电池的电压为定值,使用蓄电池时,电流(单位:A)与电阻(单位:)是反比例函数关系.下列反映电流与电阻之间函数关系的图象大致是( )
A. B. C. D.
5.如图,,直线a、b与l1、l2、l3分别相交于点A、B、C和点D、E、F,若=,DE=4,则EF的长是( )
A.B.C.6D.10
6.如表给出了二次函数()的自变量x与函数值y的部分对应值,那么方程的一个根的近似值可能是( )
A.1.09B.1.19C.1.29D.1.39
7.如图,△ABC是面积为18cm2的等边三角形,被一矩形所截,AB被截成三等分,EH∥BC,则图中阴影部分的面积为( )
A.4 cm2B.5 cm2C.6cm2D.8cm2
8.如图,矩形OABC与反比例函数(k1是非零常数,x>0)的图象交于点M,N,与反比例函数(k2是非零常数,x>0)的图象交于点B,连接OM,ON.若四边形OMBN的面积为3,则=( )
A.3B.-3C.D.
9.如图中,,,垂足为D,平分,分别交,于点F,E.若,则为( )
A.B.C.D.
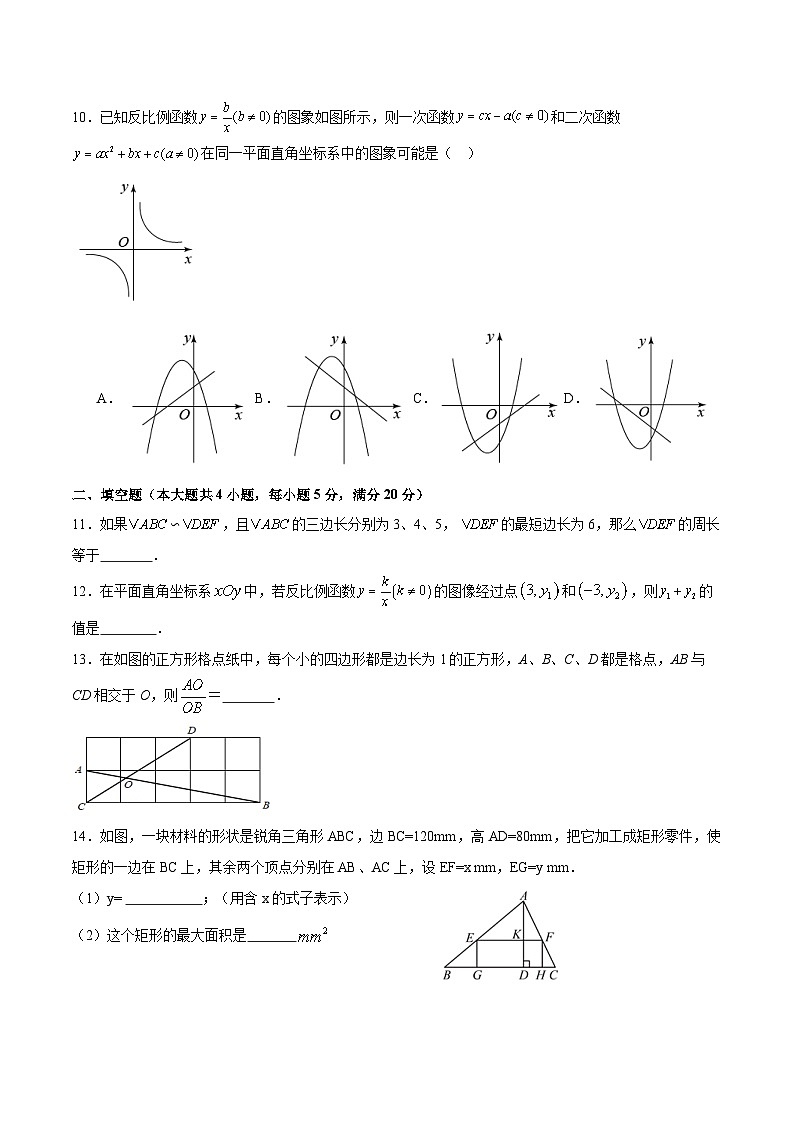
10.已知反比例函数的图象如图所示,则一次函数和二次函数在同一平面直角坐标系中的图象可能是( )
A.B.C.D.
二、填空题(本大题共4小题,每小题5分,满分20分)
11.如果∽,且的三边长分别为3、4、5, 的最短边长为6,那么的周长等于 .
12.在平面直角坐标系中,若反比例函数的图像经过点和,则的值是 .
13.在如图的正方形格点纸中,每个小的四边形都是边长为1的正方形,A、B、C、D都是格点,AB与CD相交于O,则= .
14.如图,一块材料的形状是锐角三角形ABC,边BC=120mm,高AD=80mm,把它加工成矩形零件,使矩形的一边在BC上,其余两个顶点分别在AB、AC上,设EF=x mm,EG=y mm.
(1)y= ;(用含x的式子表示)
(2)这个矩形的最大面积是
三、(本大题共2小题,每小题8分,满分16分)
15.已知,求代数式的值.
16.已知二次函数
(1)画出这个函数的图象;
(2)根据图象,直接写出当时,x的取值范围.
四、(本大题共2小题,每小题8分,满分16分)
17.如图,已知,,,,,求证:.
18.“黄金三角形”是几何历史上的瑰宝,它有两种类型,其中一种是顶角为的等腰三角形.
如图,在中,,.
(1)利用尺规作的平分线,交边于点(要求:尺规作图并保留作图痕迹,不写作法,标明字母);
(2)证明:.
五、(本大题共2小题,每小题10分,满分20分)
19.在校园科技节期间,科普员为同学们进行了水火箭的发射表演,图1是某型号水火箭的实物图,水火箭发射后的运动路线可以看作是一条抛物线.为了解水火箭的相关性能,同学们进一步展开研究.如图2建立直角坐标系,水火箭发射后落在水平地面A处.科普员提供了该型号水火箭与地面成一定角度时,从发射到着陆过程中,水火箭距离地面的竖直高度与离发射点O的水平距离的几组关系数据如下:
(1)根据上表,请确定抛物线的表达式;
(2)请计算当水火箭飞行至离发射点O的水平距离为时,水火箭距离地面的竖直高度.
20.已知:菱形中,为中点,交于,且.
(1)求证:;
(2)若,求的长.
六、(本题满分12分)
21.如图,一次函数.的图象与反比例函数的图象交于点.
(1)求反比例函数和一次函数的表达式;
(2)利用图象,直接写出不等式的解集;
(3)已知点D在x轴上,点C在反比例函数图象上.若以A、B、C、D为顶点的四边形是平行四边形,求点C的坐标.
七、(本题满分12分)
22.定义:在平面直角坐标系中,抛物线与y轴的交点坐标为,那么我们把经过点且平行于x轴的直线称为这条抛物线的极限分割线.
【特例感知】
(1)抛物线的极限分割线与这条抛物线的交点坐标为 .
【深入探究】
(2)经过点和的抛物线与y轴交于点C,它的极限分割线与该抛物线另一个交点为D,请用含m的代数式表示点D的坐标.
【拓展运用】
(3)在(2)的条件下,设抛物线的顶点为P,直线垂直平分,垂足为E,交该抛物线的对称轴于点F.,求点P的坐标.
八、(本题满分14分)
23.如图,直角△ABC中,∠BAC=90°,D在BC上,连接AD,作BF⊥AD分别交AD于E,交AC于F.
(1)如图(1),若BD=BA,求证:;
(2)如图(2),若 BD=4DC,取AB 的中点G,连接CG交AD于M,求证:①GM=2MC;
②.
x
…
1
1.1
1.2
1.3
1.4
…
y
…
1
0.49
﹣0.04
﹣0.59
﹣1.16
…
水平距离
0
3
4
10
15
20
22
27
竖直高度
0
3.24
4.16
8
9
8
7.04
3.24
相关试卷
这是一份安徽省淮北市五校联考2023-2024学年九年级上学期开学考试数学试卷(含答案),共19页。试卷主要包含了单选题,填空题,解答题等内容,欢迎下载使用。
这是一份安徽省淮北市五校联考2024届九年级上学期期末质量检测数学试卷(含答案),共10页。试卷主要包含了在中,,,,则的长为,如图是抛物线等内容,欢迎下载使用。
这是一份安徽省淮北市第二中学2023—2024学年八年级上学期期中数学测试卷,共1页。









