2021-2022学年湖北省荆州市沙市区八年级下学期期末数学试题及答案

这是一份2021-2022学年湖北省荆州市沙市区八年级下学期期末数学试题及答案，共20页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
1．（3分）下列各式中，属于最简二次根式的是（ ）
A．B．C．D．
2．（3分）若正比例函数y＝kx的图象经过点（﹣2，3），则k的值为（ ）
A．B．﹣C．D．﹣
3．（3分）下列各组数据中，由线段a，b，c组成的三角形不是直角三角形的一组是（ ）
A．a＝6，b＝8，c＝10B．a＝40，b＝50，c＝60
C．a＝，b＝1，c＝D．a＝，b＝4，c＝5
4．（3分）下列各式中，运算正确的是（ ）
A．B．C．D．
5．（3分）准备在甲，乙，丙，丁四人中选取成绩稳定的一名参加射击比赛，在相同条件下各人射击10次，已知他们的平均成绩相同，方差分别是S甲2＝0.6，S乙2＝1，S丙2＝0.8，S丁2＝2.3，则应该选择哪位运动员参赛（ ）
A．甲B．乙C．丙D．丁
6．（3分）一次函数y＝x﹣7的图象不经过的象限是（ ）
A．第一象限B．第二象限C．第三象限D．第四象限
7．（3分）如图，在▱ABCD中，AC与BD相交于O点，E为AD的中点，连接OE．若OE＝2，则CD的长度为（ ）
A．1B．2C．3D．4
8．（3分）菱形具有而一般平行四边形不具有的性质是（ ）
A．两组对边分别相等
B．两组对角分别相等
C．两条对角线互相平分
D．每一条对角线平分一组对角
9．（3分）如图，直线y＝kx+b交坐标轴于A、B两点，则不等式kx+b＜0的解集是（ ）
A．x＜﹣2B．x＜2C．x＞﹣3D．x＜﹣3
10．（3分）下列说法正确的是（ ）
A．对角线互相垂直的平行四边形是正方形
B．一组对边平行另一组对边相等的四边形是平行四边形
C．一组对边平行且一组对角相等的四边形是平行四边形
D．对角线互相垂直的四边形是菱形
二、填空题：本题共5小题，每小题3分，共15分。
11．（3分）二次根式有意义，则x的取值范围是 ．
12．（3分）已知点（﹣2，y1），（2，y2）都在直线y＝2x﹣3上，则y1 y2．（填“＜”或“＞”或“＝”）
13．（3分）某单位招聘工作人员，考试分笔试和面试两部分，笔试成绩与面试成绩按6：4记入总成绩，若小李笔试成绩为90分，面试成绩为80分，则他的总成绩是 分．
14．（3分）直角三角形的两条直角边的长分别为6和8，那么这个直角三角形斜边上的中线等于 ．
15．（3分）菲尔兹奖是享有崇高声誉的数学大奖，每四年颁奖一次，颁给二至四名成就显著的年轻数学家，对截至2014年获奖者获奖时的年龄进行统计，整理成下面的表格．
则这56个数据的中位数落在第 组．
三、解答题：本题共6小题，共45分。
16．（8分）计算：
（1）；
（2）．
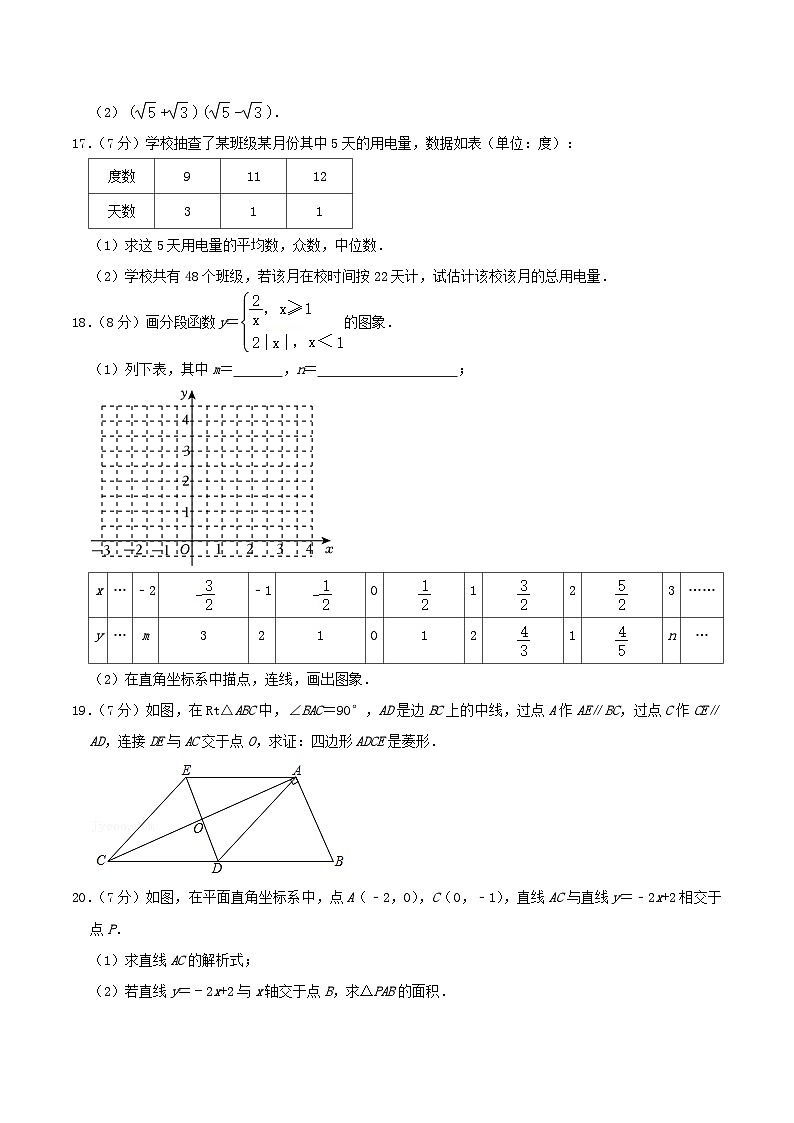
17．（7分）学校抽查了某班级某月份其中5天的用电量，数据如表（单位：度）：
（1）求这5天用电量的平均数，众数，中位数．
（2）学校共有48个班级，若该月在校时间按22天计，试估计该校该月的总用电量．
18．（8分）画分段函数y＝的图象．
（1）列下表，其中m＝ ，n＝ ；
（2）在直角坐标系中描点，连线，画出图象．
19．（7分）如图，在Rt△ABC中，∠BAC＝90°，AD是边BC上的中线，过点A作AE∥BC，过点C作CE∥AD，连接DE与AC交于点O，求证：四边形ADCE是菱形．
20．（7分）如图，在平面直角坐标系中，点A（﹣2，0），C（0，﹣1），直线AC与直线y＝﹣2x+2相交于点P．
（1）求直线AC的解析式；
（2）若直线y＝﹣2x+2与x轴交于点B，求△PAB的面积．
21．（8分）如图，在10x10的正方形网格中（小正方形的边长为1，其顶点称为格点），两端点都在格点上的线段称之为格点线段．
（1）格点线段AB长度为 ；
（2）作格点线段BD，使△BDC是等腰直角三角形且面积为4（作一种情况即可）；
（3）作格点线段BM，使得4＜BM＜5且BM平分∠ABC．
一、选择题：本题共3小题，每小题3分，共9分。
22．（3分）当时，代数式x2﹣2x+2019＝______（ ）
A．2020B．2021C．2022D．2023
23．（3分）如图，数轴上A点表示的数为﹣2，B点表示的数是1．过点B作BC⊥AB，且BC＝2，以点A为圆心，AC的长为半径作弧，弧与数轴的交点D表示的数为（ ）
A．B．+2C．﹣2D．﹣3
24．（3分）如图，在▱ABCD中，AB＝2，BC＝1，∠DAB＝60°，点P从点B出发沿路线B→C→D→A匀速运动至点A停止．已知点P的速度为每秒1个单位长度，运动时间为t秒，以P，A，B为顶点的三角形面积为S，则S与t之间的函数图象可能是（ ）
A．B．
C．D．
二、填空题：本题共3小题，每小题3分，共9分。
25．（3分）一个有进水管和出水管的容器，从某时刻开始4min内只进水不出水，在随后的8min内既进水又出水，每分钟的进水量和出水量是两个常数，容器内的水量y（L）与时间x（min）之间的关系如图所示，则每分钟的出水量为 L．
26．（3分）已知一次函数y1＝2kx+b（k，b是常数，k≠0），正比例函数y2＝mx（m是常数，m≠0）．下列四个结论：
①若一次函数的图象与正比例函数的图象平行，则k＝；
②若kb＜0，则一次函数的图象经过第一、二、四象限；
③将一次函数图象向右平移2个单位长度，则平移后的图象对应的函数解析式为y＝2kx﹣4k+b；
④若b＝2﹣k，当x＞时，y1总是小于y2，则m≥4．
其中正确的结论是 （填写序号）．
27．（3分）如图，点P是边长为2的正方形ABCD的对角线AC上一点．点Q在边CD上，且AP＝CQ，则（BP+BQ）2的最小值 ．
三、解答题：本题共1小题，共12分。
28．（12分）某公司分别在A，B两城生产同种产品，共100件．A城生产的产品总成本y（万元）与产品数量x（件）之间具有函数关系y＝kx+b．当x＝10时，y＝130；当x＝20时，y＝230．B城生产的产品每件成本为20万元，若B城生产的产品数量至少比A城生产的产品数量多40件．
（1）求k，b的值；
（2）当A，B两城生产这批产品的总成本的和最少时，求A，B两城各生产多少件？
（3）从A城把该产品运往C，D两地的费用分别为m万元/件和3万元/件；从B城把该产品运往C，D两地的费用分别为1万元/件和2万元/件．C地需要90件，D地需要10件，在（2）的条件下，直接写出A，B两城总运费的和的最小值（用含有m的式子表示）．
参考答案
一、选择题：本题共10小题，每小题3分，共30分。
1．（3分）下列各式中，属于最简二次根式的是（ ）
A．B．C．D．
【解答】解：A、＝2，能化简，不是最简二次根式，不符合题意；
B、＝，能化简，不是最简二次根式，不符合题意；
C、不能化简，是最简二次根式，符合题意；
D、＝2，能化简，不是最简二次根式，不符合题意；
故选：C．
2．（3分）若正比例函数y＝kx的图象经过点（﹣2，3），则k的值为（ ）
A．B．﹣C．D．﹣
【解答】解：∵正比例函数y＝kx的图象经过点（﹣2，3），
∴﹣2k＝3，
解得：k＝﹣，
故选：D．
3．（3分）下列各组数据中，由线段a，b，c组成的三角形不是直角三角形的一组是（ ）
A．a＝6，b＝8，c＝10B．a＝40，b＝50，c＝60
C．a＝，b＝1，c＝D．a＝，b＝4，c＝5
【解答】解：A、62+82＝102，故线段a、b、c组成的三角形，是直角三角形，不符合题意；
B、402+502≠602，故线段a、b、c组成的三角形，不是直角三角形，符合题意；
C、（）2+12＝（）2，故线段a、b、c组成的三角形，是直角三角形，不符合题意；
D、42+52＝（）2，故线段a、b、c组成的三角形，是直角三角形，不符合题意．
故选：B．
4．（3分）下列各式中，运算正确的是（ ）
A．B．C．D．
【解答】解：A、原式＝2，所以A选项不符合题意；
B、原式＝3，所以B选项不符合题意；
C、原式＝，所以C选项符合题意；
D、原式＝2，所以D选项不符合题意．
故选：C．
5．（3分）准备在甲，乙，丙，丁四人中选取成绩稳定的一名参加射击比赛，在相同条件下各人射击10次，已知他们的平均成绩相同，方差分别是S甲2＝0.6，S乙2＝1，S丙2＝0.8，S丁2＝2.3，则应该选择哪位运动员参赛（ ）
A．甲B．乙C．丙D．丁
【解答】解：∵S甲2＝0.6，S乙2＝1，S丙2＝0.8，S丁2＝2.3，
∴S甲2＜S丙2＜S乙2＜S丁2，
∴射击成绩最稳定的是甲，应该选择甲运动员参赛；
故选：A．
6．（3分）一次函数y＝x﹣7的图象不经过的象限是（ ）
A．第一象限B．第二象限C．第三象限D．第四象限
【解答】解：∵k＝1＞0，b＝﹣7＜0，
∴一次函数y＝x﹣7的图象经过第一、三、四象限，
∴一次函数y＝﹣x﹣7的图象不经过第二象限．
故选：B．
7．（3分）如图，在▱ABCD中，AC与BD相交于O点，E为AD的中点，连接OE．若OE＝2，则CD的长度为（ ）
A．1B．2C．3D．4
【解答】解：∵四边形ABCD是平行四边形，
∴AO＝CO，
∵点E是边CD的中点，
∴EO＝CD，
∵OE，
∴CD＝2OE＝4，
故选：D．
8．（3分）菱形具有而一般平行四边形不具有的性质是（ ）
A．两组对边分别相等
B．两组对角分别相等
C．两条对角线互相平分
D．每一条对角线平分一组对角
【解答】解：由菱形性质可知，每一条对角线平分一组对角；
而平行四边形不具备这样的性质；
其他A，C，B均是菱形和平行四边形共有的性质．
故选：D．
9．（3分）如图，直线y＝kx+b交坐标轴于A、B两点，则不等式kx+b＜0的解集是（ ）
A．x＜﹣2B．x＜2C．x＞﹣3D．x＜﹣3
【解答】解：由图象可以看出，x轴下方的函数图象所对应自变量的取值为x＜﹣3，
故不等式kx+b＜0的解集是x＜﹣3．
故选：D．
10．（3分）下列说法正确的是（ ）
A．对角线互相垂直的平行四边形是正方形
B．一组对边平行另一组对边相等的四边形是平行四边形
C．一组对边平行且一组对角相等的四边形是平行四边形
D．对角线互相垂直的四边形是菱形
【解答】解：A、对角线互相垂直且相等的平行四边形是正方形，所以A选项错误．
B、当一组对边平行，另一组对边相等时，该四边形可能为等腰梯形，故B选项错误．
C、由一组对边平行，一组对角相等可得另一组对边平行，所以是平行四边形，故C选项正确．
D、对角线互相垂直的平行四边形是菱形，所以D选项错误；
故选：C．
二、填空题：本题共5小题，每小题3分，共15分。
11．（3分）二次根式有意义，则x的取值范围是 x≥5 ．
【解答】解：根据题意得：x﹣5≥0，
解得x≥5．
故答案为：x≥5．
12．（3分）已知点（﹣2，y1），（2，y2）都在直线y＝2x﹣3上，则y1 ＜ y2．（填“＜”或“＞”或“＝”）
【解答】解：∵k＝2＞0，
∴y随x的增大而增大，
又∵﹣2＜2，
∴y1＜y2．
故答案为：＜．
13．（3分）某单位招聘工作人员，考试分笔试和面试两部分，笔试成绩与面试成绩按6：4记入总成绩，若小李笔试成绩为90分，面试成绩为80分，则他的总成绩是 86 分．
【解答】解：由题意可得，
小李的总成绩是：＝86（分），
故答案为：86．
14．（3分）直角三角形的两条直角边的长分别为6和8，那么这个直角三角形斜边上的中线等于 5 ．
【解答】解：∵两直角边分别为6和8，
∴斜边＝＝10，
∴斜边上的中线＝×10＝5．
故答案为：5．
15．（3分）菲尔兹奖是享有崇高声誉的数学大奖，每四年颁奖一次，颁给二至四名成就显著的年轻数学家，对截至2014年获奖者获奖时的年龄进行统计，整理成下面的表格．
则这56个数据的中位数落在第 三 组．
【解答】解：题目中数据共有56个，故中位数是按从小到大排列后第28、第29两个数的平均数，而第28、第29两个数均在第三组，
故这组数据的中位数落在第三组．
故答案为：三．
三、解答题：本题共6小题，共45分。
16．（8分）计算：
（1）；
（2）．
【解答】解：（1）原式＝4﹣2+
＝3；
（2）原式＝5﹣3
＝2．
17．（7分）学校抽查了某班级某月份其中5天的用电量，数据如表（单位：度）：
（1）求这5天用电量的平均数，众数，中位数．
（2）学校共有48个班级，若该月在校时间按22天计，试估计该校该月的总用电量．
【解答】解：（1）这5天用电量的平均数是：（9×3+11×1+12×1）÷5＝10（度）；
9度出现了3次，最多，故众数为9度；
第3天的用电量是9度，故中位数为9度；
（2）10×22×48＝10560（度），
答：估计该校该月用电10560度．
18．（8分）画分段函数y＝的图象．
（1）列下表，其中m＝ 4 ，n＝ ；
（2）在直角坐标系中描点，连线，画出图象．
【解答】解：（1）x＝﹣2代入y＝2|x|，得，y＝4，
∴m＝4，
把x＝3代入y＝，得，y＝，
∴n＝；
故答案为：4，；
（2）如图所示：
19．（7分）如图，在Rt△ABC中，∠BAC＝90°，AD是边BC上的中线，过点A作AE∥BC，过点C作CE∥AD，连接DE与AC交于点O，求证：四边形ADCE是菱形．
【解答】证明：∵AE∥BC，CE∥AD，
∴四边形ADCE是平行四边形，
∵∠BAC＝90°，AD是边BC上的中线，
∴AD＝BC＝CD，
∴平行四边形ADCE是菱形．
20．（7分）如图，在平面直角坐标系中，点A（﹣2，0），C（0，﹣1），直线AC与直线y＝﹣2x+2相交于点P．
（1）求直线AC的解析式；
（2）若直线y＝﹣2x+2与x轴交于点B，求△PAB的面积．
【解答】解：（1）设直线AC的解析式为：y＝kx+b，
把点A（2，0），C（0，1）代入得，
解得，
∴设直线AC的解析式为：y＝﹣x﹣1；
（2）∵y＝﹣2x+2与x轴交于点B，令y＝0，解得x＝1，
∴点B（1，0），
∴AB＝3，
由，解得，
∴点P（2，﹣2）．
∴S△PAB＝＝3．
21．（8分）如图，在10x10的正方形网格中（小正方形的边长为1，其顶点称为格点），两端点都在格点上的线段称之为格点线段．
（1）格点线段AB长度为 5 ；
（2）作格点线段BD，使△BDC是等腰直角三角形且面积为4（作一种情况即可）；
（3）作格点线段BM，使得4＜BM＜5且BM平分∠ABC．
【解答】解：（1）AB＝＝5，
故答案为：5；
（2）如图，△BDC即为所求；
（3）如图，线段BM即为所求．
一、选择题：本题共3小题，每小题3分，共9分。
22．（3分）当时，代数式x2﹣2x+2019＝______（ ）
A．2020B．2021C．2022D．2023
【解答】解：当时，
x2﹣2x+2019＝（x﹣1）2+2018
＝（1+﹣1）2+2018
＝3+2018
＝2021．
故选：B．
23．（3分）如图，数轴上A点表示的数为﹣2，B点表示的数是1．过点B作BC⊥AB，且BC＝2，以点A为圆心，AC的长为半径作弧，弧与数轴的交点D表示的数为（ ）
A．B．+2C．﹣2D．﹣3
【解答】解：∵CA＝＝，
∴AC＝AD＝，
∴D到原点的距离是﹣2．
∴点D所表示的数是﹣2．
故选：C．
24．（3分）如图，在▱ABCD中，AB＝2，BC＝1，∠DAB＝60°，点P从点B出发沿路线B→C→D→A匀速运动至点A停止．已知点P的速度为每秒1个单位长度，运动时间为t秒，以P，A，B为顶点的三角形面积为S，则S与t之间的函数图象可能是（ ）
A．B．
C．D．
【解答】解：当点P在BC上时，0≤t≤1，
此时三角形ABP的面积随t的增大而增大，
当点P在CD上时，1＜t≤3，
∵AB∥CD，
∴P到AB的距离不变，
∴三角形ABP的面积不变，
作DE⊥AB于E，
则∠EDA＝30°，
∴AE＝，
∴DE＝，
∴此时三角形ABP的面积为，
只有D选项符合题意，
故选：D．
二、填空题：本题共3小题，每小题3分，共9分。
25．（3分）一个有进水管和出水管的容器，从某时刻开始4min内只进水不出水，在随后的8min内既进水又出水，每分钟的进水量和出水量是两个常数，容器内的水量y（L）与时间x（min）之间的关系如图所示，则每分钟的出水量为 3.75 L．
【解答】解：由图象可得，
每分钟的进水量为：20÷4＝5（L），
每分钟的出水量为：5﹣（30﹣20）÷（12﹣4）＝5﹣10÷8＝5﹣1.25＝3.75（L），
故答案为：3.75．
26．（3分）已知一次函数y1＝2kx+b（k，b是常数，k≠0），正比例函数y2＝mx（m是常数，m≠0）．下列四个结论：
①若一次函数的图象与正比例函数的图象平行，则k＝；
②若kb＜0，则一次函数的图象经过第一、二、四象限；
③将一次函数图象向右平移2个单位长度，则平移后的图象对应的函数解析式为y＝2kx﹣4k+b；
④若b＝2﹣k，当x＞时，y1总是小于y2，则m≥4．
其中正确的结论是 ①③④ （填写序号）．
【解答】解：∵一次函数的图象与正比例函数的图象平行，
∴2k＝m，
∴k＝，故①正确；
∵kb＜0，
∴k，b异号，
当k＞0，b＜0时，一次函数的图象经过第一，三，四象限；
当k＜0，b＞0时，一次函数的图象经过第一，二，四象限；
故②错误；
将一次函数图象向右平移2个单位长度得：y＝2k（x﹣2）+b＝2kx﹣4k+b，故③正确；
若b＝2﹣k，一次函数y1＝2kx+2﹣k＝（2x﹣1）k+2，
∴一次函数y1＝2kx+b图象经过点（，2），
∵当x＞时，y1总是小于y2，
∴一次函数y1＝2kx+b图象经过一、二、三象限，
∴，解得0＜k＜2，
∴0＜2k＜4，
∴m≥4，故④正确；
故答案为①③④．
27．（3分）如图，点P是边长为2的正方形ABCD的对角线AC上一点．点Q在边CD上，且AP＝CQ，则（BP+BQ）2的最小值 8+4 ．
【解答】解：过C作CF⊥AC，使CF＝AB，连接FQ、BF，
∵四边形ABCD为正方形，
∴∠BAC＝∠ACD＝45°，
∴∠QCF＝90°﹣45°＝45°，
∴∠BAC＝∠QCF＝45°，
∵AB＝CF，AP＝CQ，
∴△ABP≌△CFQ（SAS），
∴BP＝FQ，
∴BP+BQ＝FQ+BQ≥BF，
当B、Q、F三点共线时，BQ+FQ最小，即BP+BQ最小，最小值为BF，最小值为BF，
此时过F作FH⊥BC，交BC的延长线于H，
∵∠DCH＝90°，∠QCF＝45°，
∴∠FCH＝45°，
∵∠CHF＝90°，
∴△CFH是等腰直角三角形，
∵CF＝AB＝2，
∴CH＝FH＝，
∴BH＝BC+CH＝2+，
在Rt△BFH中，
由勾股定理，得BF2＝BH2+FH2＝（2+）2+（）2＝8+4，
∴（BP+BQ）2的最小值是8+4；
故答案为：8+4．
三、解答题：本题共1小题，共12分。
28．（12分）某公司分别在A，B两城生产同种产品，共100件．A城生产的产品总成本y（万元）与产品数量x（件）之间具有函数关系y＝kx+b．当x＝10时，y＝130；当x＝20时，y＝230．B城生产的产品每件成本为20万元，若B城生产的产品数量至少比A城生产的产品数量多40件．
（1）求k，b的值；
（2）当A，B两城生产这批产品的总成本的和最少时，求A，B两城各生产多少件？
（3）从A城把该产品运往C，D两地的费用分别为m万元/件和3万元/件；从B城把该产品运往C，D两地的费用分别为1万元/件和2万元/件．C地需要90件，D地需要10件，在（2）的条件下，直接写出A，B两城总运费的和的最小值（用含有m的式子表示）．
【解答】解：（1）由题意，得：，
解得：．
（2）设A，B两城生产这批产品的总成本的和为W万元，
则W＝10x+30+20（100﹣x）＝﹣10x+2030，
由B城生产的产品数量至少比A城生产的产品数量多40件，
得：100﹣x≥x+40，
解得：x≤30，
∵﹣10＜0，
∴W随x的增大而减小，
∴当x＝30时，W最小，即A，B两城生产这批产品的总成本的和为最少，
∴A城生产了30件产品，B城生产了100﹣30＝70件产品．
答：当A，B两城生产这批产品的总成本的和最少时，A城生产了30件产品，B城生产了70件产品．
（3）设从A城运往C地的产品数量为n件，A，B两城总运费的和为P，
则从A城运往D地的产品数量为（30﹣n）件，从B城运往C地的产品数量为（90﹣n）件，从B城运往D地的产品数量为（10﹣30+n）件，
由题意得：，
解得：20≤n≤30，
∴P＝mn+3（30﹣n）+（90﹣n）+2（10﹣30+n），
整理得：P＝（m﹣2）n+140，
根据一次函数的性质分以下两种情况：
①当0＜m≤2，20≤n≤30时，P随n的增大而减小，
则n＝30时，P取最小值，最小值为30（m﹣2）+140＝30m+80；
②当m＞2，20≤n≤30时，P随n的增大而增大，
则n＝20时，P取最小值，最小值为20（m﹣2）+140＝20m+100．
答：当0＜m≤2时，A，B两城总运费的和为（30m+80）万元；当m＞2时，A，B两城总运费的和为（20m+100）万元．组别
第一组
第二组
第三组
第四组
年龄段（岁）
27＜x≤31
31＜x≤34
34＜x≤37
37＜x≤40
频数（人）
8
11
17
20
度数
9
11
12
天数
3
1
1
x
…
﹣2
﹣1
0
1
2
3
……
y
…
m
3
2
1
0
1
2
1
n
…
组别
第一组
第二组
第三组
第四组
年龄段（岁）
27＜x≤31
31＜x≤34
34＜x≤37
37＜x≤40
频数（人）
8
11
17
20
度数
9
11
12
天数
3
1
1
x
…
﹣2
﹣1
0
1
2
3
……
y
…
m
3
2
1
0
1
2
1
n
…