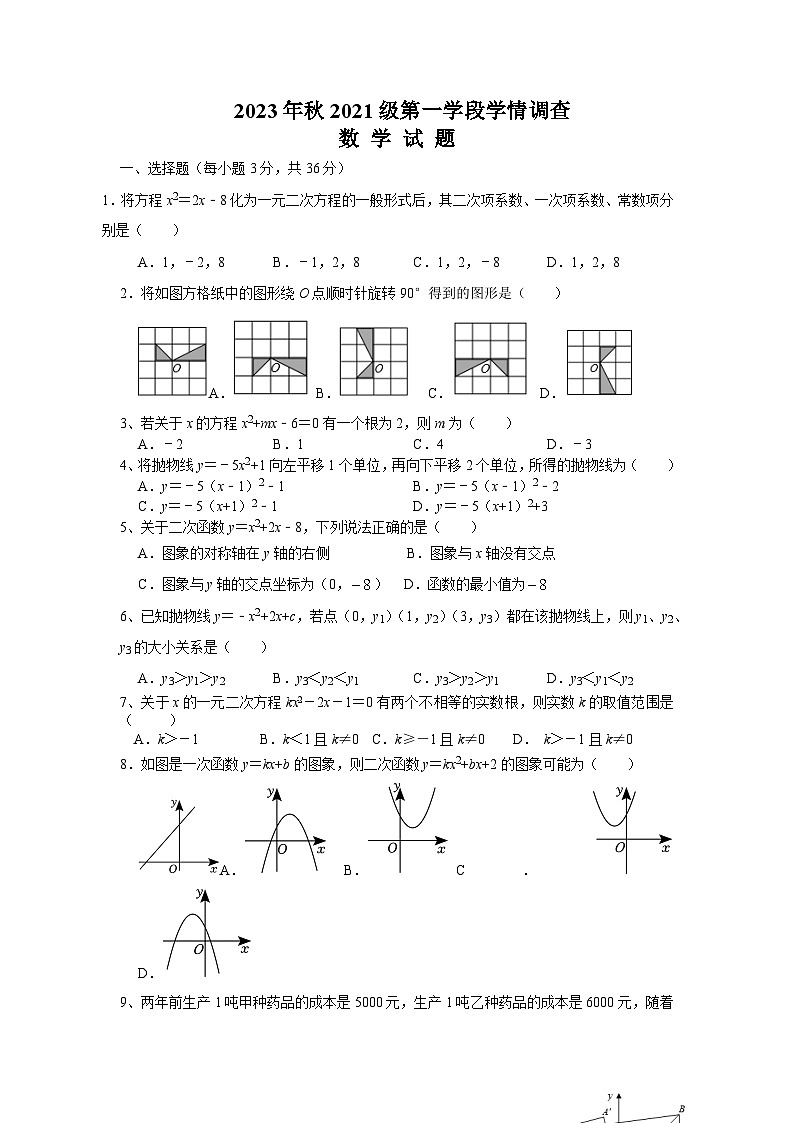
2023-2024学年四川省绵阳市游仙区富乐学校九年级（上）学情调查数学试卷（10月份）.

这是一份2023-2024学年四川省绵阳市游仙区富乐学校九年级（上）学情调查数学试卷（10月份）.，共6页。
选择题（每小题3分，共36分）
1．将方程x2＝2x﹣8化为一元二次方程的一般形式后，其二次项系数、一次项系数、常数项分别是（ ）
A．1，﹣2，8B．﹣1，2，8C．1，2，﹣8D．1，2，8
2．将如图方格纸中的图形绕O点顺时针旋转90°得到的图形是（ ）
A．B．C．D．
3、若关于x的方程x2+mx﹣6＝0有一个根为2，则m为（ ）
A．﹣2B．1C．4D．﹣3
4、将抛物线y＝﹣5x2+1向左平移1个单位，再向下平移2个单位，所得的抛物线为（ ）
A．y＝﹣5（x﹣1）2﹣1B．y＝﹣5（x﹣1）2﹣2
C．y＝﹣5（x+1）2﹣1D．y＝﹣5（x+1）2+3
5、关于二次函数y＝x2+2x﹣8，下列说法正确的是（ ）
A．图象的对称轴在y轴的右侧 B．图象与x轴没有交点
C．图象与y轴的交点坐标为（0，） D．函数的最小值为
6、已知抛物线y＝﹣x2+2x+c，若点（0，y1）（1，y2）（3，y3）都在该抛物线上，则y1、y2、y3的大小关系是（ ）
A．y3＞y1＞y2B．y3＜y2＜y1C．y3＞y2＞y1D．y3＜y1＜y2
7、关于x的一元二次方程kx2－2x－1＝0有两个不相等的实数根，则实数k的取值范围是（ ）
A．k＞－1B．k＜1且k≠0 C．k≥－1且k≠0 D． k＞－1且k≠0
8．如图是一次函数y＝kx+b的图象，则二次函数y＝kx2+bx+2的图象可能为（ ）
A．B．C．D．
10题图
9、两年前生产1吨甲种药品的成本是5000元，生产1吨乙种药品的成本是6000元，随着生产技术的进步，现在生产1吨甲种药品的成本是3000元，生产1吨乙种药品的成本是3600元，如果甲药品成本的年平均下降率为，乙药品成本的年平均下降率，则与的大小关系为（ ）。
A．B． C． D．没法比较
10、如图，在平面直角坐标系中，点A（2，0），点B在第一象限，AB⊥OA，AB＝OA，将
△OAB绕点O按逆时针方向旋转105°得到△OA'B'，连点B'的坐标（ ）．
A. B. C. D.
11、对于一元二次方程ax2+bx+c＝0（a≠0），下列说法错误的是（ ）
A、若a-b+c＝0，则方程必有一根为x＝；
B、若x0是一元二次方程ax2+bx+c＝0的根，则
C、若方程ax2+bx+c＝0（a≠0）两根为x1，x2且满足x1≠x2≠0，则方程cx2+bx+a＝0（c≠0），必有实根；
D、若方程ax2+c＝0有两个不相等的实根，则方程ax2+bx+c＝0无实根；
12、二次函数y=ax2＋bx＋c（a，b，c为常数，且a≠0）中的x与y的部分对应值如下表： 下列结论：①ac>0；②当x＞1时，y的值随x值的增大而减小．③方程ax2＋（b－1）x＋c=0两根分别是；④ ,其中正确的个数为（ ）
A．1个 B．2个 C．3个 D．4个
二、填空题（每小题4分，共24分）
13、若方程x2﹣6x+8＝0的两个根分别是某等腰三角形的底边和腰长，则该等腰三角形的周长为_____________。
14、如图，要设计一幅宽30cm，长40cm的图案，其中有两横两竖的彩条，横、竖彩条的宽度比为3：2．如果要使彩条所占面积是图案面积的四分之一，求彩条的宽度，设横、竖彩条的宽度分别为3x cm和2x cm，则可列方程为 ．
15、在一次实心球的测试中，李聪明同学掷实心球时实心球行进的高度（单位：米）与水平距离（单位：米）之间的关系式是,李聪明同学这次掷实心球的距离为____________米。
16、如图所示，把一个直角三角尺ABC绕着60º角的顶点B顺时针旋转，使直角顶点C与AB的延长线上的点D重合．给出以下结论：① ∠CBE=60º；② BE=CD；③ △ACD是等腰三角形；④ CD⊥BE；⑤ A、C、E可能不共线．其中正确结论的序号是 ．
16题图
14题图
18题图
17、已知关于x的方程x2+（2m﹣1）x+m2＝0有实数根．且α，β是方程的两个实数根，实数m使得α2+β2﹣αβ＝13成立，则m=______________。
18、如图，在平面直角坐标系中，抛物线，经过点A（1，0）、点B（0，3），点P是该抛物线上一动点，其横坐标为n．若抛物线C1在点P左侧部分（包括点P）的最低点的纵坐标为4﹣n，则n的值为______________．
三、解答题(共90分）
19、（共16分）解方程（1）． （2） 2x2+1＝4x（配方法）．
20、（12分）在如图所示的平面直角坐标系中，有△ABC．点A（3，3）、B（1，1）、C（4，2）
（1）将△ABC向x轴负方向平移4个单位得到△A1B1C1，画出图形并写出点A1的坐标．
（2）以原点O为旋转中心，将△ABC顺时针旋转90°后得到△A2B2C2，画出图形并写出点A2的坐标．
（3）△A2B2C2可以看作是由△A1B1C1先向右平移4个单位，然后以原点O为旋转中心，顺时针旋转90°得到的．除此之外，△A2B2C2还可以由△A1B1C1经过旋转变换得到，请在图中找出旋转中心．并写出其旋转中心的坐标
21、（12分）已知关于x的方程x2﹣（k+2）x+2k＝0．
（1）求证：k取任何实数时，方程总有实数根，并把方程的根用含k的式子表示出来；
（2）若△ABC为直角三角形，且斜边a＝4，另两边长b，c恰好是这个方程的两个根，求出k的值。
22、（12分）甲、乙两人进行羽毛球比赛，羽毛球飞行的路线为抛物线的一部分，如图，甲在O点正上方1m的P处发出一球，羽毛球飞行的高度y（m）与水平距离x（m）之间满足函数解析式y＝a（x﹣4）2+h，已知点O与球网的水平距离为5m，球网的高度1.55m．
（1）当a＝时，①求h的值．②通过计算判断此球能否过网．
（2）若甲发球过网后，羽毛球飞行到与点O的水平距离为7m，离地面的高度为m的Q处时，乙扣球成功，求a的值．
23、（12分）小郭在景区销售一种旅游纪念品，已知每件进价为6元，当销售单价定为8元时，每天可以销售200件．市场调查反映：销售单价每提高1元，日销量将会减少10件，物价部门规定：销售单价不能超过13元，设该纪念品的销售单价为x（元），日销量为y（件），日销售利润为w（元）．
（1）直接写出y与x的函数关系式．
（2）要使日销售利润为720元，销售单价应定为多少元？
（3）求日销售利润w（元）与销售单价x（元）的函数关系式，当x为何值时，日销售所获利润最大，并求出此时的最大利润．
24、（12分）问题：如图①，在等边三角形ABC内有一点P，且PA＝2，PB＝，PC＝1，求∠BPC的度数和等边三角形ABC的边长．
赵明同学的思路是：将△BPC绕点B逆时针旋转60°，画出旋转后的图形（如图②），连接PP′，可得△P′PB是等边三角形，而△PP′A又是直角三角形（由勾股定理的逆定理可证），可得∠AP′B＝ °，所以∠BPC＝∠AP′B＝ °，还可根据△ABP的三边长度得到△ABP是直角三角形，进而求出等边三角形ABC的边长为 ，问题得到解决．
解决下列问题：
（1）根据赵明同学的思路填空：∠AP′B＝ °，∠BPC＝∠AP′B＝ °，等边三角形ABC的边长为 ．
（2）类比探究，如图③，在正方形ABCD内有一点P，且PA＝，PB＝，PC＝2．求：①∠BPC的度数；②正方形ABCD的边长．
25、(共14分）如图，抛物线经过点C（4，0）、点B（0，3）、点A（）
（1）求抛物线的解析式，并直接写出直线BC的解析式；
（2）如图，点E是直线BC上方抛物线上的一动点，当△BEC面积最大时，请求出点E的坐标和△BEC面积的最大值；
（3）在（2）的结论下，过点E作y轴的平行线交直线BC于点M，连接AM，点Q是抛物线对称轴上的动点，在抛物线上是否存在点P，使得以P、Q、A、M为顶点的四边形是平行四边形？如果存在，请直接写出点P的坐标；如果不存在，请说明理由．
x
﹣1
0
1
3
y
﹣1
3
5
3