一线三等角相似、三垂直模型--2024年中考数学压轴题专题

这是一份一线三等角相似、三垂直模型--2024年中考数学压轴题专题，文件包含一线三等角相似三垂直模型压轴题专题原卷版docx、一线三等角相似三垂直模型压轴题专题解析版docx、一线三等角相似三垂直模型压轴题专题学生版pdf、一线三等角相似三垂直模型压轴题专题解析版pdf等4份试卷配套教学资源，其中试卷共44页， 欢迎下载使用。

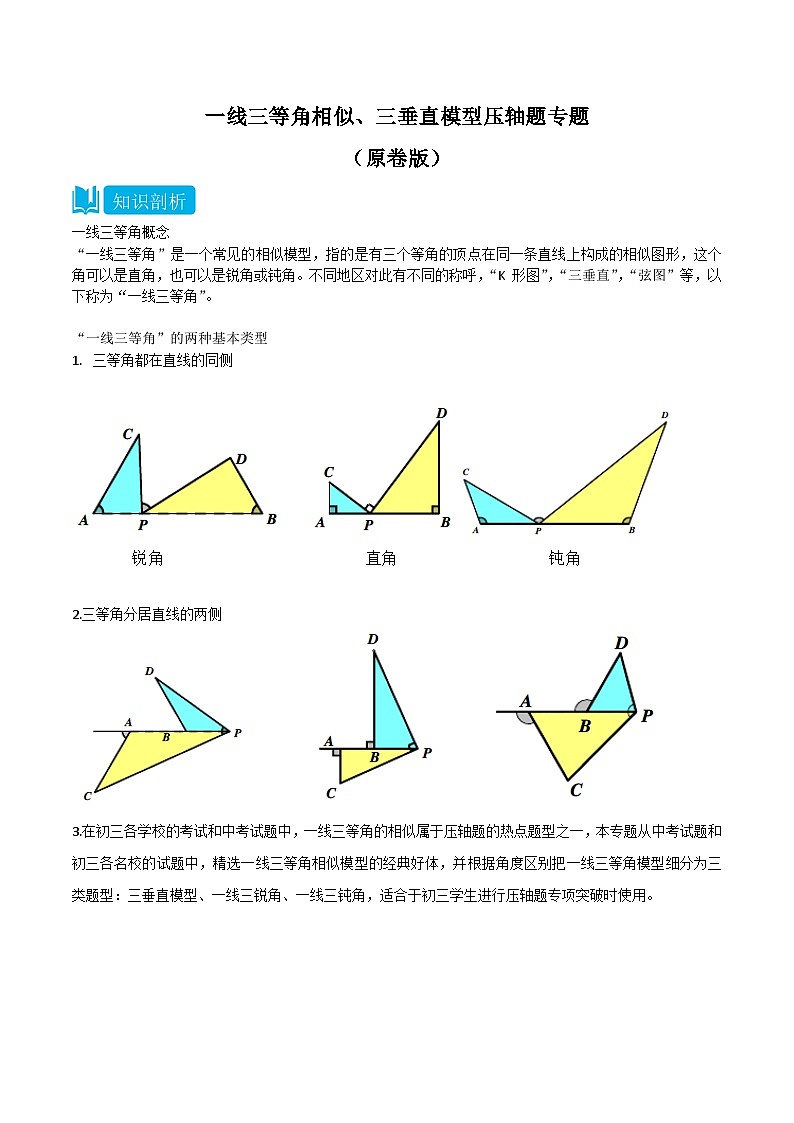
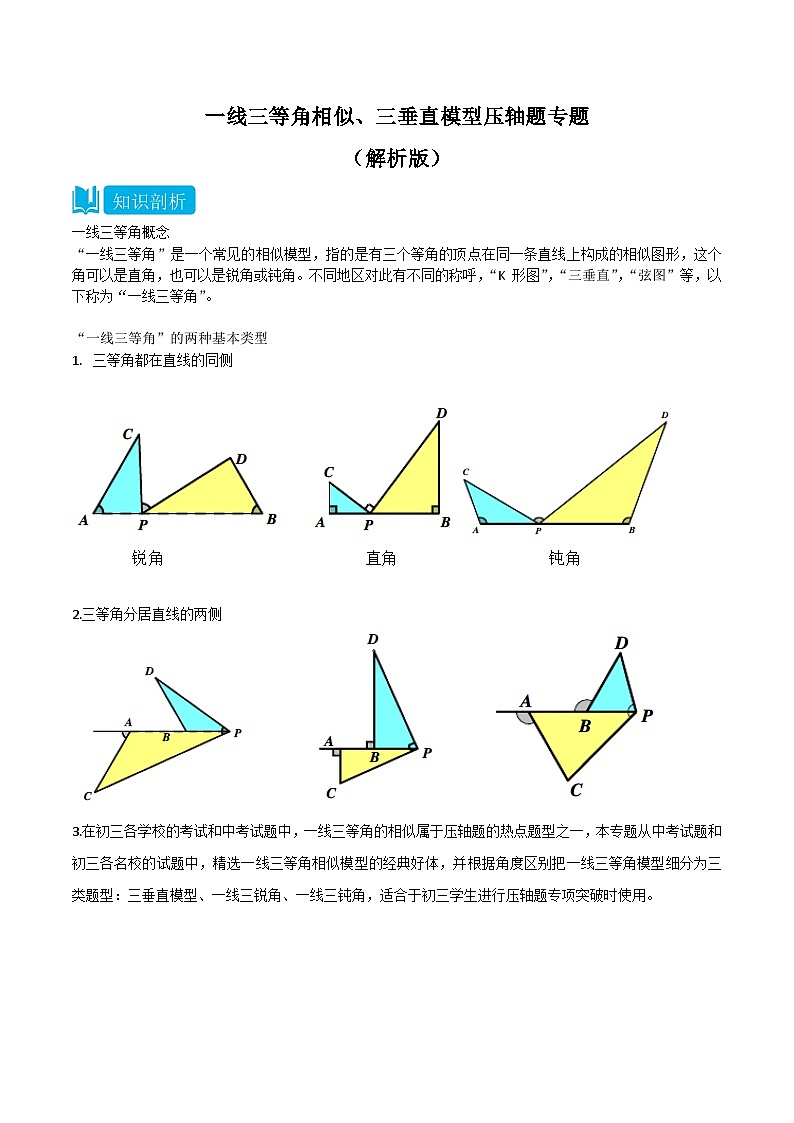
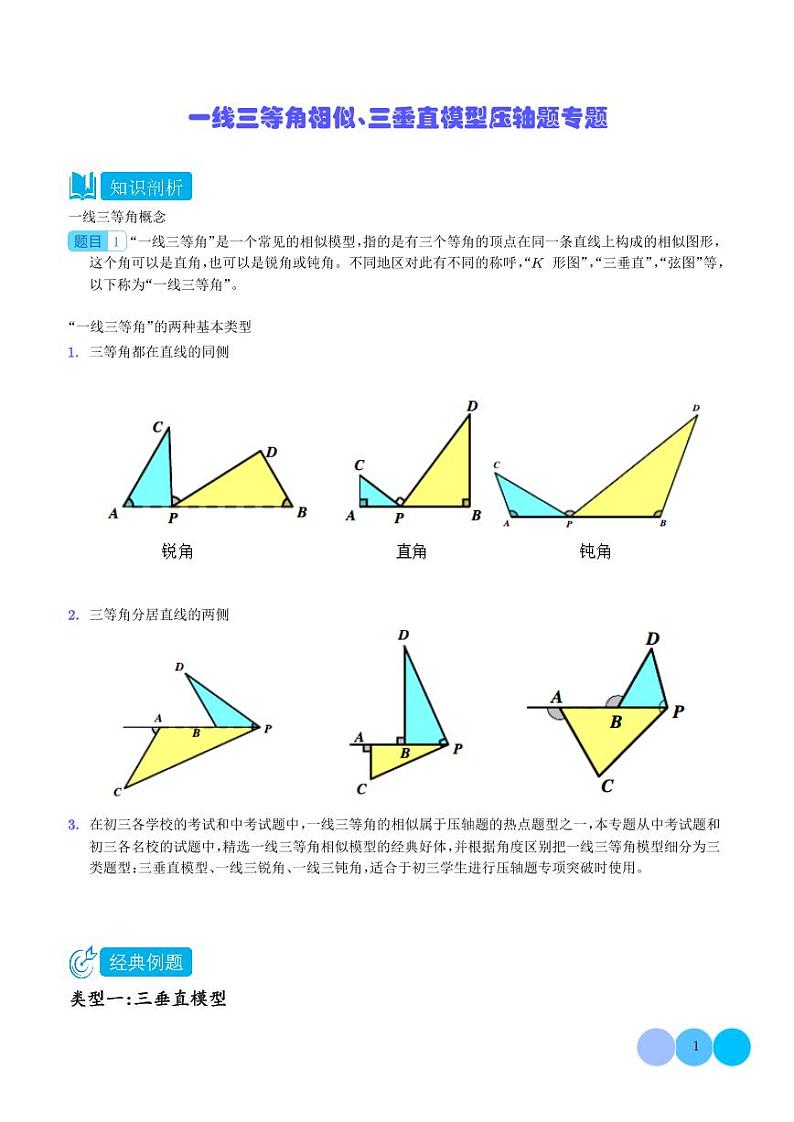
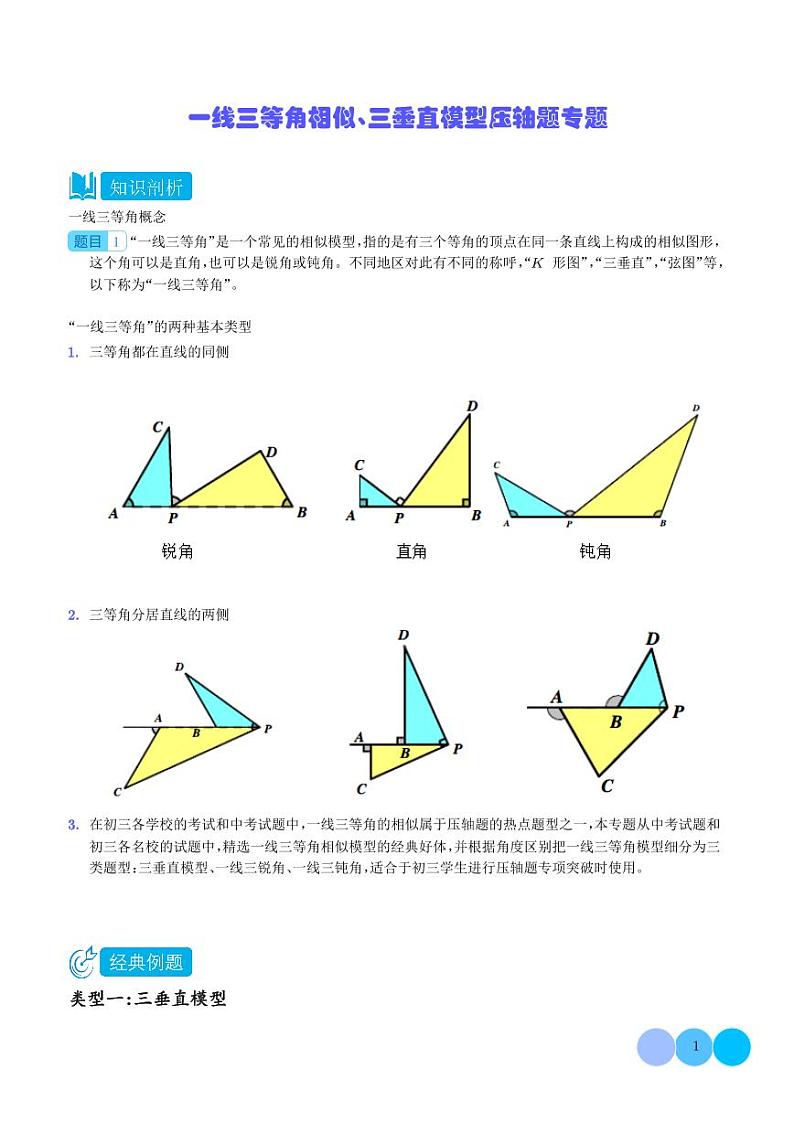
一线三等角概念
“一线三等角”是一个常见的相似模型，指的是有三个等角的顶点在同一条直线上构成的相似图形，这个角可以是直角，也可以是锐角或钝角。不同地区对此有不同的称呼，“K 形图”，“三垂直”，“弦图”等，以下称为“一线三等角”。
“一线三等角”的两种基本类型
三等角都在直线的同侧


2.三等角分居直线的两侧
3.在初三各学校的考试和中考试题中，一线三等角的相似属于压轴题的热点题型之一，本专题从中考试题和初三各名校的试题中，精选一线三等角相似模型的经典好体，并根据角度区别把一线三等角模型细分为三类题型：三垂直模型、一线三锐角、一线三钝角，适合于初三学生进行压轴题专项突破时使用。
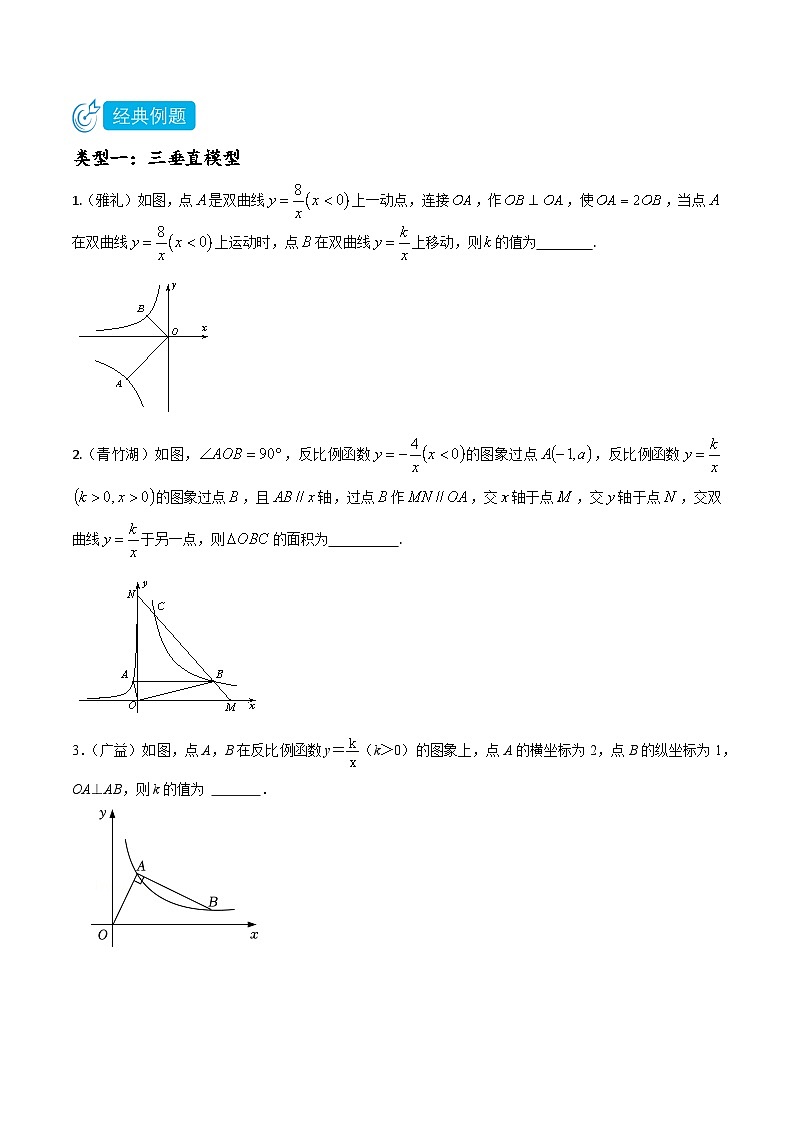
类型一：三垂直模型
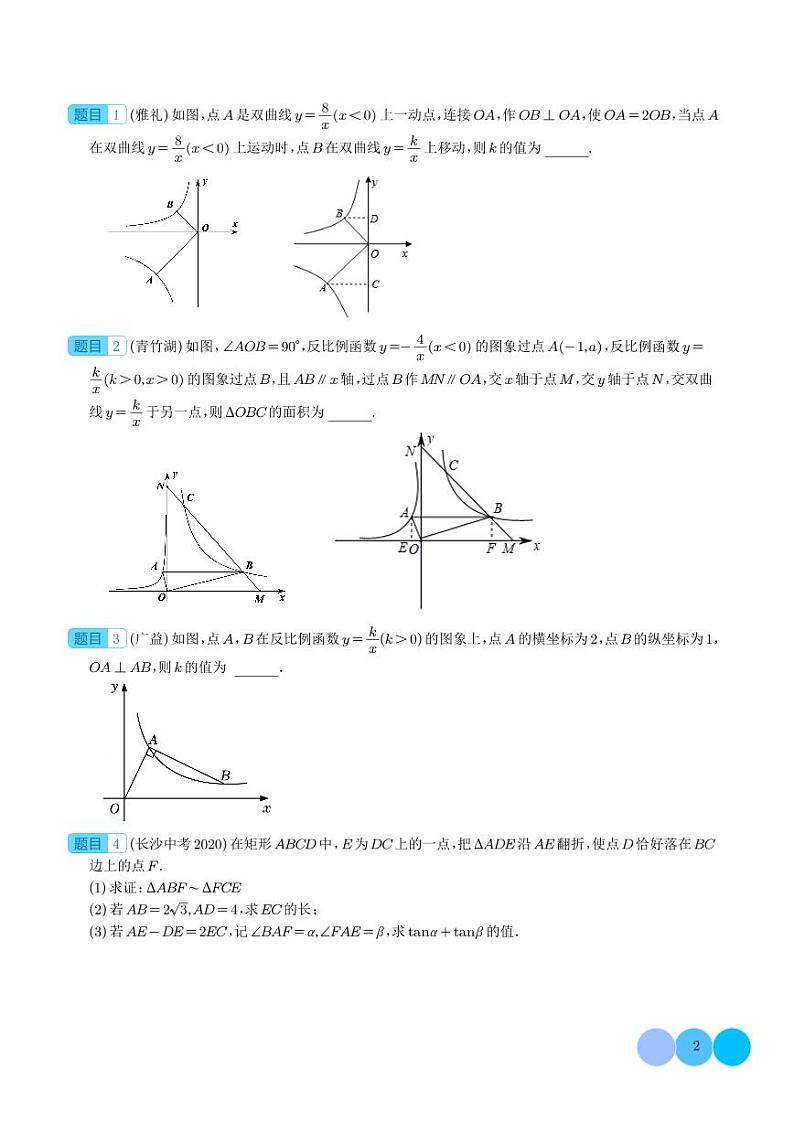
1.（雅礼）如图，点是双曲线上一动点，连接，作，使，当点在双曲线上运动时，点在双曲线上移动，则的值为 .

【解答】解：过A作AC⊥y轴于点C，过B作BD⊥y轴于点D，∵点A是反比例函数y＝（x＜0）上的一个动点，点B在双曲线y＝上移动，∴S△AOC＝×|﹣8|＝4，S△BOD＝|k|，∵OB⊥OA，
∴∠BOD+∠AOC＝∠AOC+∠OAC＝90°，∴∠BOD＝∠OAC，且∠BDO＝∠ACO，
∴△AOC∽△OBD，∵OA＝2OB，∴＝（）2＝，∴＝，∴|k|＝2．
∴k＜0，∴k＝﹣2，故答案为：﹣2．
2.（青竹湖）如图，，反比例函数的图象过点，反比例函数的图象过点，且轴，过点作，交轴于点，交轴于点，交双曲线于另一点，则的面积为 .

【解答】解：∵反比例函数 的图象过点A（﹣1，a），∴a＝﹣＝4，
∴A（﹣1，4），过A作AE⊥x轴于E，BF⊥x轴于F，∴AE＝4，OE＝1，∵AB∥x轴，∴BF＝4，
∵∠AOB＝90°，∴∠EAO+∠AOE＝∠AOE+∠BOF＝90°，∴∠EAO＝∠BOF，∴△AEO∽△OFB，
∴＝，∴OF＝16，∴B（16，4），∴k＝16×4＝64，∵直线OA过A（﹣1，4），
∴直线AO的解析式为y＝﹣4x，∵MN∥OA，∴设直线MN的解析式为y＝﹣4x+b，∴4＝﹣4×16+b，
∴b＝68，∴直线MN的解析式为y＝﹣4x+68，∵直线MN交x轴于点M，交y轴于点N，
∴M（17，0），N（0，68），解得，或，∴C（1，64），
∴△OBC的面积＝S△OMN﹣S△OCN﹣S△OBM＝﹣﹣＝510，
故答案为510．
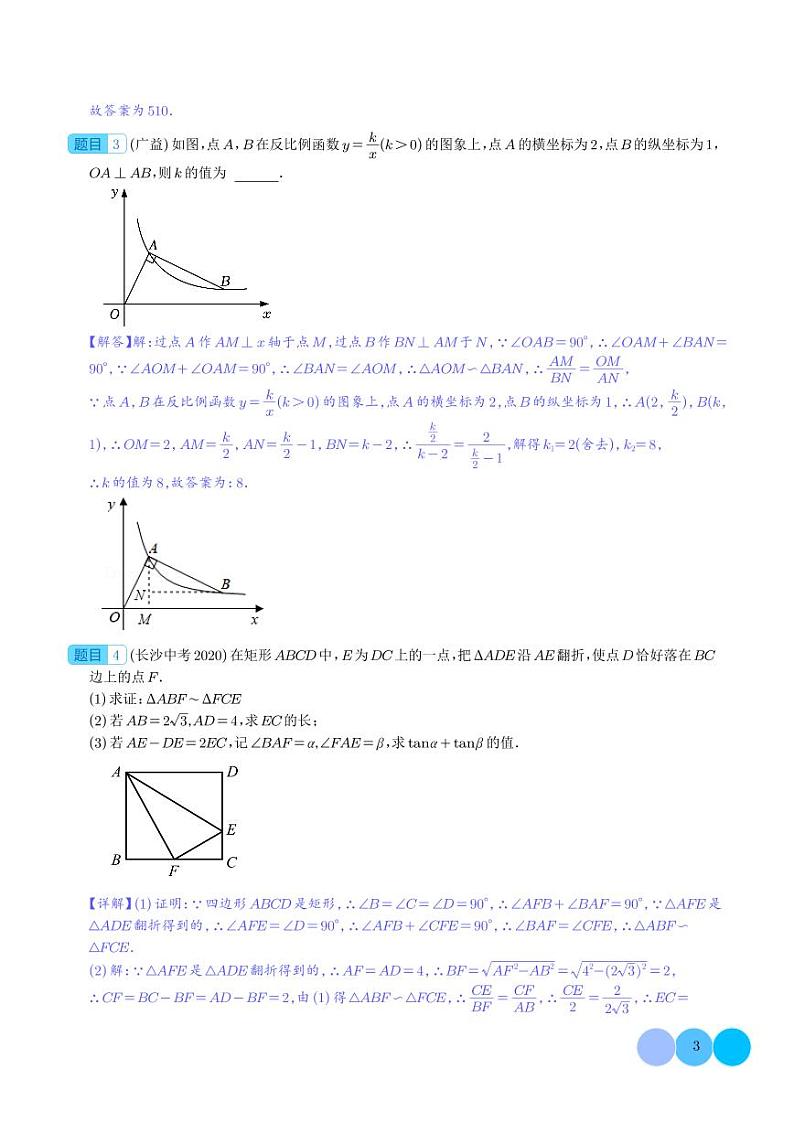
3．（广益）如图，点A，B在反比例函数y＝（k＞0）的图象上，点A的横坐标为2，点B的纵坐标为1，OA⊥AB，则k的值为 ．
【解答】解：过点A作AM⊥x轴于点M，过点B作BN⊥AM于N，∵∠OAB＝90°，∴∠OAM+∠BAN＝90°，∵∠AOM+∠OAM＝90°，∴∠BAN＝∠AOM，∴△AOM∽△BAN，∴＝，
∵点A，B在反比例函数y＝（k＞0）的图象上，点A的横坐标为2，点B的纵坐标为1，∴A（2，），B（k，1），∴OM＝2，AM＝，AN＝﹣1，BN＝k﹣2，∴＝，解得k1＝2（舍去），k2＝8，
∴k的值为8，故答案为：8．
4．（长沙中考2020）在矩形ABCD中，E为上的一点，把沿AE翻折，使点D恰好落在BC边上的点F．
（1）求证：
（2）若，求EC的长；
（3）若，记，求的值．
【详解】（1）证明：∵四边形ABCD是矩形，∴∠B=∠C=∠D=90°，∴∠AFB+∠BAF=90°，∵△AFE是△ADE翻折得到的，∴∠AFE=∠D=90°，∴∠AFB+∠CFE=90°，∴∠BAF=∠CFE，∴△ABF∽△FCE．
（2）解：∵△AFE是△ADE翻折得到的，∴AF=AD=4，∴BF=，
∴CF=BC-BF=AD-BF=2，由（1）得△ABF∽△FCE，∴，∴，∴EC=．
（3）解：由（1）得△ABF∽△FCE，∴∠CEF=∠BAF=，∴tan+tan=，
设CE=1，DE=x，∵，∴AE=DE+2EC=x+2，AB=CD=x+1，AD=
∵△ABF∽△FCE，∴，∴，∴，∴，
∴，∴x2-4x+4=0，解得x=2，∴CE=1，CF=，EF=x=2，
AF= AD==，∴tan+tan==．
5.（广益）矩形中，，，将矩形折叠，使点落在点处，折痕为．
（1）如图1，若点恰好在边上．
①求证：△∽△；②求的长；
（2）如图2，若是的中点，的延长线交于点，求的长．

图1 图2
【解答】解：（1）①∵四边形ABCD是矩形，∴∠B＝∠C＝∠BAD＝90°，∴∠BPE+∠BEP＝90°，
由折叠知，∠DPE＝∠BAD＝90°，∴∠BPE+∠CPD＝90°，∴∠BEP＝∠CPD，∵∠B＝∠C＝90°，
∴△EBP∽△PCD；
②∵四边形ABCD是矩形，∴∠B＝∠C＝90°，CD＝AB＝8，BC＝AD＝12，由折叠知，PE＝AE，DP＝
AD＝12，在Rt△DPC中，CP＝＝4，∴BP＝BC﹣CP＝12﹣4，在Rt△PBE中，PE2﹣BE2＝BP2，∴AE2﹣（8﹣AE）2＝（12﹣4）2，∴AE＝18﹣6；
（2）如图，过点P作GH∥BC交AB于G，交CD于H．则四边形AGHD是矩形，设EG＝x，则BG＝4﹣x，∵∠A＝∠EPD＝90°，∠EGP＝∠DHP＝90°，∴∠EPG+∠DPH＝90°，∠DPH+∠PDH＝90°，
∴∠EPG＝∠PDH，∴△EGP∽△PHD，∴＝＝＝＝，∴PH＝3EG＝3x，DH＝AG＝4+x，
在Rt△PHD中，PH2+DH2＝PD2，∴（3x）2+（4+x）2＝122，解得x＝（负值已经舍弃），
∴BG＝4﹣＝，在Rt△EGP中，GP＝＝，∵GH∥BC，∴△EGP∽△EBF，
∴＝，∴＝，∴BF＝3．
6．（长郡）如图，在平面直角坐标系中，为原点，已知点是射线上一点，，点是轴正半轴上一点，，连接，经过点且与相切于点，与边相交于另一点．
(1)若圆心在轴上，求的半径；
(2)若圆心在轴的上方，且圆心到轴的距离为，求的半径；
(3)在（2）的条件下，若，点是经过点，，的抛物线上的一个动点，点为轴上的一个动点，若满足的点共有个，求点的横坐标的取值范围．
【解答】解：（1）∵圆心A在x轴上，⊙A经过点O且与QP相切于点P，∴PQ⊥x轴，OP为直径，
∵tan∠POC＝1，，∴PQ＝OP，∵在Rt△OPQ中，．
∴OP＝18．∴⊙A的半径为9；
（2）如图所示，过点A作AM⊥x轴于点M，过点Q作QB⊥x轴于B，连接AP，
∵PQ是⊙A的切线，∴AP⊥PQ，则∠APQ＝90°，∵AM⊥x轴，QB⊥x轴，∴∠AMP＝∠PBC＝90°，
∴∠PAM＝90°﹣∠APM＝∠QPB，∴△APM∽△PBQ，∴，∵tan∠POC＝1，QB＝18，
∴OB＝QB＝18，∵AM＝2，设MP＝MO＝x，∴PB＝18﹣2x，∴，解得x＝3或x＝6，
∴MO＝3或MO＝x，∴A（3，2）或A（6，2），∴AP＝＝或AP＝＝2．
∴半径为或2．
（3）
∵OP＜10，∴BO＝3，P（6，0），∴A（3，2），∵tan∠POC＝1，设D（a，a），∵，
∴（3﹣a）2+（2﹣a）2＝13，解得：a＝0或a＝5，∴D（5，5），设抛物线解析式为y＝ax2+bx，
将点P（6，0），D（5，5）代入得，，解得：，∴y＝﹣x2+6x，
∵点F可能在点O的左边或点P的右边，，则|KFM|＝，
设直线MF：或，联立，，
得或，当或，
解得：或，∴直线MF：或，令y＝0，解得：或，
∴或．
7.（麓山国际）有一边是另一边的倍的三角形叫做智慧三角形，这两边中较长边称为智慧边，这两边的夹角叫做智慧角．
（1）已知Rt△ABC为智慧三角形，且Rt△ABC的一边长为，则该智慧三角形的面积为 ；
（2）如图①，在△ABC中，∠C＝105°，∠B＝30°，求证：△ABC是智慧三角形；
（3）如图②，△ABC是智慧三角形，BC为智慧边，∠B为智慧角，A（3，0），点B，C在函数y＝上（x＞0）的图象上，点C在点B的上方，且点B的纵坐标为．当△ABC是直角三角形时，求k的值．
【解答】解：（1）如图1，设∠A＝90°，AC≤AB，S△ABC＝AC•AB，
①若AC＝，
i）AB＝AC＝2，∴S＝，
ii）BC＝AC＝2，则AB＝，∴S＝，
②若AB＝，
i）AB＝AC，即AC＝，∴S＝，
ii）BC＝AB＝2，则AC＝∴S＝，
③若BC＝，若AB＝AC＝＝1，∴S＝，
若AB＝AC，AB＝，，S＝××＝，
故答案为：或1或或或．
（2）证明：如图2，过点C作CD⊥AB于点D，∴∠ADC＝∠BDC＝90°，在Rt△BCD中，∠B＝30°，
∴BC＝2CD，∠BCD＝90°﹣∠B＝60°，∵∠ACB＝105°，∴∠ACD＝∠ACB﹣∠BCD＝45°，
∴Rt△ACD中，AD＝CD，∴AC＝，∴，
∴△ABC是智慧三角形．
（3）∵△ABC是智慧三角形，BC为智慧边，∠B为智慧角，∴BC＝AB，∵△ABC是直角三角形，
∴AB不可能为斜边，即∠ACB≠90°∴∠ABC＝90°或∠BAC＝90°
①当∠ABC＝90°时，过B作BE⊥x轴于E，过C作CF⊥EB于F，过C作CG⊥x轴于G，如图3，
∴∠AEB＝∠F＝∠ABC＝90°，∴∠BCF+∠CBF＝∠ABE+∠CBF＝90°，∴∠BCF＝∠ABE，
∴△BCF∽△ABE，∴，设AE＝a，则BF＝AE＝a，∵A（3，0），
∴OE＝OA+AE＝3+a，∵B的纵坐标为，即BE＝，
∴CF＝BE＝2，CG＝EF＝BE+BF＝，B（3+a，），
∴OG＝OE﹣GE＝OE﹣CF＝3+a﹣2＝1+a，∴C（1+a，），
∵点B、C在在函数y＝上（x＞0）的图象上，∴（3+a）＝（1+a）（+a）＝k
解得：a1＝﹣2（舍去），a2＝1，∴k＝，
②当∠BAC＝90°时，过C作CM⊥x轴于M，过B作BN⊥x轴于N，如图4，
∴∠CMA＝∠ANB＝∠BAC＝90°，∴∠MCA+∠MAC＝∠MAC+∠NAB＝90°，
∴∠MCA＝∠NAB，∴△MCA∽△NAB，∵BC＝，∴2AB2＝BC2＝AB2+AC2，
∴AC＝AB，∴△MCA≌△NAB（AAS），∴AM＝BN＝，∴OM＝OA﹣AM＝3﹣，
设CM＝AN＝b，则ON＝OA+AN＝3+b，∴C（3﹣，b），B（3+b，），
∵点B、C在在函数y＝上（x＞0）的图象上，∴（3﹣）b＝（3+b）＝k
解得：b＝，∴k＝18+15，综上所述，k的值为或。
类型二：一线三锐角
8.（师大梅溪湖）如图，在△ABC中，，，，，，则CD的长为________.（提示，作辅助线构造一线三等角的相似）
【详解】解：在CD上取点F，使，
，，由，，
，，且，
，，∽，
， ，，
又， ，
∽，，
又，，或舍去，
经检验：符合题意，．故答案为：5．
5．（青竹湖）如图，在△ABC中，∠B＝∠ACB＝45°，AB＝6，点D是BC上一点，作DE⊥AD交射线AC于E，DF平分∠ADE交AC于F．
（1）求证：AB•CF＝BD•CD；
（2）如图2，当∠AED＝75°时，求CF的长；
（3）若CD＝3BD，求．
【解答】（1）证明：如图1中，
∵DE⊥AD，∴∠ADE＝90°，∵DF平分∠ADE，∴∠ADF＝∠FDC＝45°，∵∠ADC＝∠B+∠BAD＝∠ADF+∠FDC，∠B＝∠ADF＝45°，∴∠BAD＝∠FDC，∵∠B＝∠C，∴△ABD∽△DCF，
∴，∴AB•CF＝BD•CD．
（2）解：如图2中，过点A作AH⊥BC于H．
∵∠B＝∠C＝45°，∴AB＝AC＝6，∴BC＝AB＝12，∵AH⊥BC，∴BH＝CH＝6，AH＝BH＝CH＝6，∵AD⊥DE，∠AED＝75°，∴∠ADE＝90°，∠DAE＝15°，∴∠ADH＝∠DAE+∠C＝60°，
∴∠DAH＝30°，DH＝AH•tan30°＝2，∴BD＝6+2，CD＝6﹣2，∵AB•CF＝BD•CD，
∴6•CF＝（6+2）（6﹣2），∴CF＝2．
（3）如图2﹣1中，过点A作AH⊥BC于H，过点E作EG⊥CD于G．设BD＝a，则CD＝3a，BC＝4a．
∵AB＝AC，∠BAC＝90°，∴AH＝HB＝HC＝2a，DH＝a，∠C＝∠B＝45°，∵∠AHD＝∠ADE＝∠DGE＝90°，∴∠ADH+∠EDG＝90°，∠EDG+∠DEG＝90°，∴∠ADH＝∠DEG，∴△ADH∽△DEG，设EG＝CG＝y，CD＝3a，则DG＝3a+y，∴，∴，解得y＝3a，∴CG＝EG＝3a，EC＝3a，
∵CF＝＝a，∴AF＝AC﹣CF＝2a﹣a＝a，EF＝CF+CE＝a+3a＝a，∴＝．
10.（广益）如图1，已知直线（k为常数，k≠0）与x轴相交于点A，点B与点A关于y轴对称，点C在y轴的正半轴上，，连接AC，BC。
（1）求△ABC的面积及sin∠ACB；
（2）如图2，已知P，Q分别是线段AC，BC上的一动点，且始终满足∠POQ=60°。
①求AP·BQ的值及△CPQ面积的最大值；
②当△AOP与△OQP的面积相等时，抛物线经过P，Q两点，经过点P的直线满足：
对于任意的实数x，都有成立。记，若函数与x轴相交于M，N两点，且线段MN≤1，求a的取值范围。
【解答】解：（1）∵y＝kx+2k＝k（x+2），∴A（﹣2，0），∵OC＝，∴OC＝2，
在Rt△AOC中，∵tan∠CAB＝＝，∴∠CAB＝60°，由对称性得，OB＝OA，BC＝AC，
∴△ABC是等边三角形，∴∠ACB＝60°∴sin∠ACB＝，
∴S△ABC＝AB•OC＝＝4；
（2）如图2，
①由（1）知，△ABC是等边三角形，∴∠CAB＝∠ABC＝60°，∴∠APO+∠AOP＝120°，
∵∠POQ＝60°，∴∠BOQ+∠AOP＝120°，∴∠APO＝∠BOQ，∴△AOP∽△BQO，
∴＝，∴AP•BQ＝OA•OB＝4，作PD⊥BC于D，∴PD＝PC•sin∠ACB＝PC，
∵S△CPQ＝CQ•PD＝（AC﹣AP）（BC﹣BQ）＝（4﹣AP）（4﹣BQ）＝5﹣（AP+BQ）
＝5﹣（AP+），∵（a﹣b）2≥0，∴a2+b2﹣2ab≥0，∴a2+b2≥2ab，
∴+≥2••＝4，即AP+≥4，∴当AP＝2时，S△CPQ最大＝5﹣4＝；
②如图3，
∵S△AOP＝S△OQP，∴OA•PG＝•PH，∴OA•AP•sin60°＝OQ•OP•sin60°，∴2AP＝OP•OQ，
∵△AOP∽△BQO，＝，∴OP＝•OQ，∴2AP＝•OQ2，∴OQ＝2，∴P（﹣1，）
如图4，
由题意得，b＝0，a+c＝，﹣m+n＝，∴y1＝ax2+（），y2＝mx+（m+），
∵对于任意的实数x，都有y1≥y2成立，∴ax2﹣mx﹣（m+a）＝0，Δ＝m2+4a（m+a）＝0，
∴m＝﹣2a，∴w＝ax2+（）+mx+（m+）＝ax2+（）﹣2ax﹣2a+
＝ax2﹣2ax+（2﹣3a），当ax2﹣2ax+（2﹣3a）＝0时，设M（b，0），N（c，0），∴b+c＝2，
bc＝，∵MN≤1，∴MN2≤1，∴（b﹣c）2≤1，即（b+c）2﹣4bc≤1，∴4﹣4•≤1，
又a＞0，∴0＜a≤．
类型三：一线三钝角
11.（2016年长沙中考）如图，直线l：y=﹣x+1与x轴，y轴分别交于A，B两点，点P，Q是直线l上的两个动点，且点P在第二象限，点Q在第四象限，∠POQ=135°．
（1）求△AOB的周长；
（2）设AQ=t＞0，试用含t的代数式表示点P的坐标；
（3）当动点P，Q在直线l上运动到使得△AOQ与△BPO的周长相等时，记tan∠AOQ=m，若过点A的二次函数y=ax2+bx+c同时满足以下两个条件：
①6a+3b+2c=0；
②当m≤x≤m+2时，函数y的最大值等于，求二次项系数a的值．

【解答】解：（1）在函数y＝﹣x+1中，令x＝0，得y＝1，∴B（0，1），令y＝0，得x＝1，
∴A（1，0），则OA＝OB＝1，AB＝，∴△AOB周长为1+1+＝2+．
∵OA＝OB，∴∠ABO＝∠BAO＝45°，∴∠PBO＝∠QAO＝135°，设∠POB＝x，则∠OPB＝
∠AOQ＝135°﹣x﹣90°＝45°﹣x，∴△PBO∽△OAQ，∴＝，∴PB＝＝，
过点P作PH⊥OB于H点，则△PHB为等腰直角三角形，∵PB＝，∴PH＝HB＝，
∴P（﹣，1+）．
（3）由（2）可知△PBO∽△OAQ，若它们的周长相等，则相似比为1，即全等，∴PB＝OA，
∴＝1，∴t＝1，同理可得Q（1+，﹣），∴m＝＝﹣1，∵抛物线经过点A，
∴a+b+c＝0，又∵6a+3b+2c＝0，∴b＝﹣4a，c＝3a，对称轴x＝2，取值范围﹣1≤x+1，
①若a＞0，则开口向上，由题意x＝﹣1时取得最大值＝2+2，即（﹣1）2a+（﹣1）b+c＝2+2，解得a＝．
②若a＜0，则开口向下，由题意x＝2时取得最大值2+2，即4a+2b+c＝2+2，解得a＝﹣2﹣2．
综上所述所求a的值为或﹣2﹣2．
12．（2023·浙江宁波·校考三模）点C在的延长线上，且，
（1）如图（1），若，求证：；
【思考探究】
（2）如图（2），若，，若，求的值；
【拓展延伸】
如图（3），连接，若，，若，求n的值．
【解答】解：（1）∵，，∴，
在和中，，∴．
（2）如图，过点E作，交于点F，

∵，∴，，∴，
∴，∵，∴，∴，
由（1）可得：，∴，设，则，，
∴，∴，故答案为：．
（3）如图，延长至点F，使得，连接，

则，∴，∵，∴，∴，
设，则，，，∴，
∴，又∵，∴，∴，∴．