2024-2025学年吉林省长春市汽开区九年级（上）期中数学试卷 含详解

这是一份2024-2025学年吉林省长春市汽开区九年级（上）期中数学试卷 含详解，共18页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

1．（3分）点A在数轴上的位置如图所示，将点A向右移动3个单位长度得到点B，则点B表示的数是（ ）
A．1B．2C．3D．4
2．（3分）近几年全国各省市都在发展旅游业，据文旅部数据中心统计，今年长春市“十一”黄金周期间游客接待量约为1230万人次，将“1230万”这个数字用科学记数法表示为（ ）
A．1.23×107B．12.3×106C．1.23×105D．1.23×103
3．（3分）下列图形中不是位似图形的是（ ）
A．B．
C．D．
4．（3分）某中学校园文化艺术节歌唱比赛有15名同学参赛，得分前8名的同学进入决赛，经过角逐，这15名同学的得分各不相同，小明知道自己的得分后，要判断自己能否进入决赛，还需要知道这15名同学得分的（ ）
A．平均数B．方差C．众数D．中位数
5．（3分）“立身以立学为先，立学以读书为本”为了鼓励全民阅读，某校图书馆开展阅读活动，自阅读活动开展以来，进馆阅读人次逐月增加，第一个月进馆260人次，第三个月进馆540人次，若进馆人次的月增长率相同，求进馆人次的月增长率．设进馆人次的月增长率为x，依题意可列方程（ ）
A．260（1+x）2＝540
B．260（1+x）+260（1+x）2＝540
C．260（1+x+x2）＝540
D．260+260（1+x）+260（1+x）2＝540
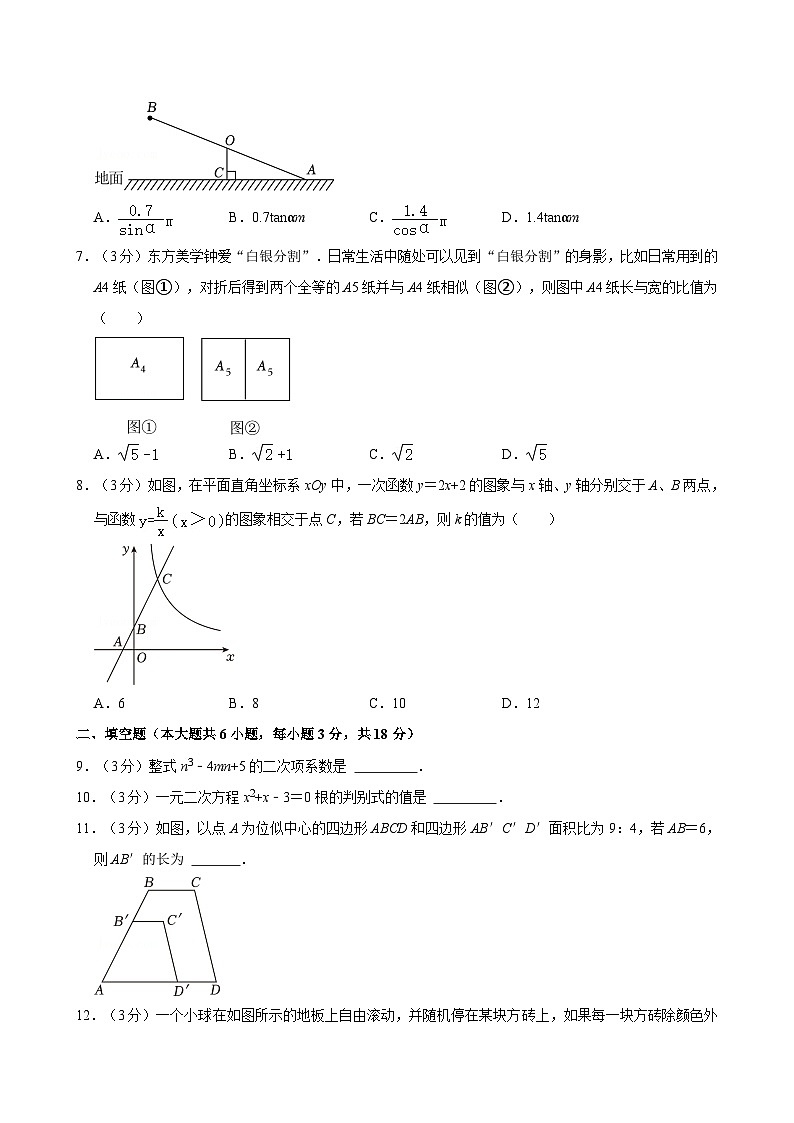
6．（3分）为倡导全民健身，某小区在公共活动区域安装了健身器材，其中跷跷板很受欢迎．如图，点O为跷跷板AB中点，支柱OC垂直于地面，垂足为C，AC＝0.7m，跷跷板的一端A落到地面时与地面的夹角∠OAC＝α，则点B离地面的距离是（ ）
A．B．0.7tanαmC．D．1.4tanαm
7．（3分）东方美学钟爱“白银分割”．日常生活中随处可以见到“白银分割”的身影，比如日常用到的A4纸（图①），对折后得到两个全等的A5纸并与A4纸相似（图②），则图中A4纸长与宽的比值为（ ）
A．B．C．D．
8．（3分）如图，在平面直角坐标系xOy中，一次函数y＝2x+2的图象与x轴、y轴分别交于A、B两点，与函数的图象相交于点C，若BC＝2AB，则k的值为（ ）
A．6B．8C．10D．12
二、填空题（本大题共6小题，每小题3分，共18分）
9．（3分）整式n3﹣4mn+5的二次项系数是 ．
10．（3分）一元二次方程x2+x﹣3＝0根的判别式的值是 ．
11．（3分）如图，以点A为位似中心的四边形ABCD和四边形AB′C′D′面积比为9：4，若AB＝6，则AB′的长为 ．
12．（3分）一个小球在如图所示的地板上自由滚动，并随机停在某块方砖上，如果每一块方砖除颜色外完全相同，那么小球最终停留在白色方砖上的概率是 ．
13．（3分）据欧几里得的《原本》记载，形如x2+ax＝b2的方程的图解法是：画Rt△ABC，使∠ACB＝90°，，AC＝b，再以点B为圆心BC长为半径画圆弧，交斜边AB于点D，则该方程的一个正根是线段AD的长．当a＝6，b＝5时，AD的长为 ．
14．（3分）如图，在△ABC中，∠C＝90°，AC＝2，BC＝3，点D是AB的中点，连结CD，AE⊥CD分别交CD、AB于点F、E．给出下面四个结论：
①AB＝2CD；
②△ECF∽△ABC；
③△ACF和△EDF是以点F为位似中心的位似图形；
④．
上述结论中，所有正确结论的序号是 ．
三、解答题（本大题共10小题，共78分）
15．（6分）计算：．
16．（8分）解方程：
（1）3x2﹣5x＝0；
（2）x2﹣2x﹣4＝0．
17．（8分）“十一”期间，我校（1）班学生通过抽取卡片的方式决定去三个场馆中的两个场馆进行锻炼．三个场馆分别用字母A、B、C表示．现把分别印有A、B、C的三张卡片（除字母外，其余都相同）背面朝上，洗匀放好．从中随机抽取一张（不放回），再从中随机抽取一张．请用列表或画树状图的方法，求抽到的两张卡片恰好是B和C的概率．
18．（8分）如图，AC与BD相交于点O，分别连结AB和CD，∠A＝∠D．
（1）求证：△AOB∽△DOC．
（2）若AO＝5，DO＝3，△AOB的面积为50，△DOC的面积为 ．
19．（8分）图①、图②、图③均是2×2的正方形网格，每个小正方形的边长均为1，其顶点称为格点，△ABC的顶点均在格点上．按要求完成下列问题，在给定的网格中作图，作图时要求只用无刻度的直尺，保留作图痕迹．
（1）图①中，点D是BC的中点，在AB边上确定一点E，连结DE，使∠BDE＝∠BCA．
（2）图②中，在AB边上确定一点F，连结CF，使．
（3）图③中，在AB边上确定一点M，连结CM，使∠BCM＝∠BAC．
20．（8分）随着科技的不断进步，人工智能（AI）正逐渐渗透到我们的生活和工作．从家庭助手到自动驾驶汽车，再到智能医疗，AI的应用前景广阔且充满无限可能．某人工智能科技体验馆在十一假期间为学生们制订了丰富多彩的体验活动，团体票收费标准为：如果人数不超过10人，人均费用为240元；如果人数超过10人，每增加1人，人均费用降低5元，但人均旅游费用不得低于170元．
（1）若有14人参加旅游，人均费用是 元．
（2）某兴趣小组的学生们去参加体验活动，团体票的费用共3600元，求参加活动的学生人数．
21．（8分）图①是一款可调节椅背的沙发椅，它可以减轻使用者的脊椎压力．图②是它的侧面示意图，椅背BC＝70cm，将椅背角度从110°调节到150°（即∠ABC＝110°，∠ABD＝150°）时，分别过点C、D作CE⊥AB于点E，DF⊥AB于点F，求水平方向增加的距离EF长．（结果精确到lcm；参考数据：sin70°≈0.9，cs70°≈0.3，tan70°≈2.7，）
22．（8分）模型思想是一种数学的思考方法，是运用数学的语言和方法，通过抽象、简化而建立，能近似刻画并解决实际问题，以下是某数学小组应用模型思想解决数学问题的过程．
【模型探究】
探究1．如图①，点D是△ABC中BC上的一点，且，过点B作BF∥AC交AD的延长线于点F，则＝ ．
探究2．如图②，在△ABC中，∠BAC＝90°，AB＝AC．∠DAE＝45°，交BC于点D、E．求证：AE2＝DE•BE．
【模型应用】
如图③，点E为正方形ABCD边AD的中点，连结BE，作∠EBF＝45°，交CD于点F，连结AC，分别交BE、BF于点M、N，若AB＝2，则MN＝ ．
23．（8分）如图，△ABC中，AB＝AC＝3，BC＝4．动点P、Q分别从点A、C同时出发，点P以每1个单位长度的速度沿AC向终点C运动，点Q沿折线CB﹣BA向终点A运动，在CB上的速度为每秒2个单位长度，在BA上的速度为每秒3个单位长度，连结PQ．设点的运动时间为t（s）（t＞0）．
（1）用含t的代数式表示BQ的长．
（2）求点A到边BC的距离．
（3）cs∠ACB＝ ．
（4）当∠CPQ≠90°时，以PQ为对角线作矩形PEQF，且点E在AC边上，当∠EPQ＝∠ACB时，求t的值．
24．（8分）在平面直角坐标系中，直线l1：y＝2x与直线l2：y＝﹣3x+2n﹣1相交于点M，点A是线l1上的动点，且横坐标为n．
（1）若n＝3时，求点M的坐标．
（2）当点A与点M重合时，求直线l2的解析式．
（3）当点A与点M不重合时，过点A作x轴和直线l1的垂线，分别交直线l2于点B、D，过点B作BC⊥y轴交直线l1于点C，连结CD．
①tan∠DCA＝ ．
②以AC和CD为边作▱ACDE，若S▱ACDE＝8时，直接写出n的值．
2024-2025学年吉林省长春市汽开区九年级（上）期中数学试卷
参考答案
一、选择题（本大题共8小题，每小题3分，共24分）
1．【解答】解：﹣1+3＝2，
点B表示的数是2．
故选：B．
2．【解答】解：1230万＝12300000＝1.23×107．
故选：A．
3．【解答】解：对应顶点的连线相交于一点的两个相似多边形叫位似图形．
根据位似图形的概念，A、B、C三个图形中的两个图形都是位似图形；
D中的两个图形不符合位似图形的概念，对应边不平行，故不是位似图形．
故选：D．
4．【解答】解：由题意可得，
这15个不同的成绩按从小到大排序后，中位数就是第8个数据，
故只要知道自己的成绩和中位数，就可以知道是否进入决赛，
故选：D．
5．【解答】解：根据题意可得260（1+x）2＝540，
故选：A．
6．【解答】】解：如图，过点B作BD垂直底面于点D，
∵BD⊥AD，OC⊥AD，
∴BD∥OC，
∴△AOC∽△ABD，
∴，
∵点O为跷跷板AB的中点，
∴AC＝AD，
∴OC是△ABD的中位线，
在△AOC中，∵AC＝0.7m，∠OAC＝α，
∴OC＝AC•tanα＝0.7tanα（m），
∴BD＝2OC＝14tanαm，
故选：D．
7．【解答】解：设A4纸的宽为x，长为y，则A5的宽为y，长为x，
∵A5纸和A4纸相似，
∴y：x＝x：y，即x2＝y2，
∴x：y＝1：，
∴y：x＝：1，即A4纸的长与宽比值是．
故选：C．
8．【解答】解：一次函数y＝2x+2中，
当x＝0时，y＝2，
∴OB＝2，
当y＝0时，2x+2＝0，
∴x＝﹣1，
∴OA＝1，
如图，过点C作CD⊥y轴于D，
∵OA⊥y轴，
∴OA∥CD，
∴△CDB∽△AOB，
∴＝＝，即＝＝，
∵BC＝2AB，
∴CD＝2，BD＝4，
∴C（2，6），
∴k＝2×6＝12．
故选：D．
二、填空题（本大题共6小题，每小题3分，共18分）
9．【解答】解：依题意，整式的三次项为：n3，二次项为：﹣4mn，常数项为：5，
所以二次项系数为：﹣4．
故答案为：﹣4．
10．【解答】解：一元二次方程x2+x﹣3＝0，
∵a＝1，b＝1，c＝﹣3，
∴Δ＝b2﹣4ac＝12﹣4×1×（﹣3）＝1+12＝13，
故答案为：13．
11．【解答】解：∵以点A为位似中心的四边形ABCD和四边形AB′C′D′面积比为9：4，
∴四边形ABCD与四边形AB′C′D′的相似比为3：2，
∴AB：AB'＝3：2，
∵AB＝6，
∴AB′＝4．
故答案为：4．
12．【解答】解：观察这个图可知：白色区域（5块）的面积占总面积（9块）的，
则它最终停留在白砖上的概率是，
故答案为：．
13．【解答】解：在Rt△ABC中，∠ACB＝90°，BC＝a，AC＝b，BD＝BC＝a，
当a＝6，b＝5时，AC＝5，BD＝BC＝a＝3，
则AD＝AB﹣BD＝AB﹣3，
在Rt△ABC中，由勾股定理得：AB＝＝＝，
∴AD＝﹣3，
故答案为：﹣3．
14．【解答】解：∵∠ACB＝90°，点D是AB的中点，则由斜边中线定理可知AB＝2CD，故①结论正确；
∵∠ACB＝90°，点D是AB的中点，
∴BD＝CD，
∴∠B＝∠FCB，
又∠CFE＝∠ACB＝90°，
∴△ECF∽△ABC，故②结论正确；
∵AE⊥CD，
∴∠CAE＝90°﹣∠ACD＝∠BCD＝∠B，
∵AC＝2，BC＝3，由勾股定理可得：AB＝＝，
＝，
∵∠CAF＝∠B，
∴△CAF∽△ABC，
∴，即，
从而可得AF＝，CF＝，，
∵△ECF∽△ABC，
∴，即＝，
∴EF＝，
∴DF＝CD﹣CF＝＝，
∴＝，
∴△ACF和△EDF是以点F为位似中心的位似图形，故③结论不正确；
∵AE＝AF+EF＝＝+＝，
∴S四边形ACED＝＝，
∴S△ABC＝AC×BC＝3，
∴S四边形ACED＝S△ABC，故④结论不正确．
综上，正确的有①②．
故答案为：①②．
三、解答题（本大题共10小题，共78分）
15．【解答】解：．
＝
＝
＝1．
16．【解答】解：（1）3x2﹣5x＝0，
x（3x﹣5）＝0，
x＝0或3x﹣5＝0，
∴x1＝0，；
（2）x2﹣2x﹣4＝0，
x2﹣2x＝4，
x2﹣2x+1＝5，
（x﹣1）2＝5，
x﹣1＝±，
∴，．
17．【解答】解：列表如下：
共有6种等可能的结果，其中抽到的两张卡片恰好是B和C的结果有：（B，C），（C，B），共2种，
∴抽到的两张卡片恰好是B和C的概率为．
18．【解答】（1）证明：∵AC与BD相交于点O，
∴∠AOB＝∠DOC，
又∵∠A＝∠D，
∴△AOB∽△DOC；
（2）解：∵△AOB∽△DOC，
∴，
∴，
解得S△DOC＝18．
∴△DOC的面积为18，
故答案为：18．
19．【解答】解：（1）如图①，取格点N，连接DN，交AB于点E，即点E为所求点；
（2）如图②，取格点H，连接CH，交AB于F，即点F为所求点；
（3）如图③，取格点H，P，Q，连接CH，PQ，PQ与AB于点M，即点M为所求点．
20．【解答】解：（1）由题意得：240﹣（14﹣10）×5＝240﹣20＝220，
即若有14人参加旅游，人均费用是22元，
故答案为：220；
（2）设参加活动的学生人数为x人，
由题意得：x[240﹣5（x﹣10）]＝3600，
整理得：x2﹣58x+720＝0，
解得：x1＝18，x2＝40，
当x1＝18时，240﹣5×（18﹣10）＝200＞170，符合题意；
当x2＝40时，240﹣5×（40﹣10）＝90＜170，不符合题意，舍去；
答：参加活动的学生人数为18人．
21．【解答】解：由题意得：BC＝BD＝70cm，
∵∠ABC＝110°，
∴∠CBE＝180°﹣110°＝70°，
∵∠ABD＝150°，
∴∠DBF＝180°﹣150°＝30°，
在Rt△CBE与Rt△DBF中，
∵CE⊥AB，DF⊥AB，
∴BE＝BC•cs∠CBE，
BF＝BD•cs∠DBF，
∴EF＝BF﹣BE＝BD•cs∠DBF﹣BC•cs∠CBE
＝70×cs30°﹣70×cs70°
≈39（cm）．
答：水平方向增加的距离EF长约39cm．
22．【解答】【模型探究】
探究1．解：∵BF∥AC，
∴△BDF∽△CDA，
∴，
∵，
∴＝，
故答案为：；
探究2．证明：在Rt△ABC中，
∵AB＝AC，
∴∠B＝∠DAE＝45°．
又∵∠AEB＝∠BEA，
∴△ADE∽△BAE．
∴，
∴AE2＝DE•BE；
【模型应用】解：∵四边形ABCD是正方形，
∴AD＝AB＝BC＝2，∠BAC＝∠ACB＝45°，∠ABC＝90°，
∴AC＝AB＝2，
∵点E为正方形ABCD边AD的中点，
∴AE＝＝1，
∴BE＝＝，
∵AD∥BC，
∴△AME∽△CMB，
∴＝，
∴＝，
∴BM＝，CM＝，
∵∠MBN＝∠BCM＝45°，∠BMN＝∠CMB，
∴△BMN∽△CMB，
∴，
∴＝，
∴MN＝，
故答案为：．
23．【解答】解：（1）当0＜t≤2时，BQ＝4﹣2t；
当2＜t≤3时，BQ＝3（t﹣2）＝3t﹣6；
（2）如图1，过点A作AD⊥BC于点D，
∵AB＝AC＝3，BC＝4，
∴，
在Rt△ACD中，由勾股定理得：，
∴点A到边BC的距离为；
（3）在Rt△ACD中，AC＝3，CD＝2，
∴cs∠ACD＝＝，
∴；
故答案为：；
（4）（i）如图2，当0＜t≤2时，AP＝t，CQ＝2t，
在矩形PEQF中，∠PEQ＝90°，
∴∠CEQ＝90°，
在Rt△CEQ中，，
∵，
∴，
∵CQ＝2t，
∴，
当∠C＝∠CPQ时，CQ＝PQ，
∵，
∴，
∴；
（ii）如图3，当2＜t≤3时，
∵∠C＝∠EPQ，
∴PQ∥BC，
∴，
∵AB＝AC，
∴AP＝AQ，
∴PC＝BQ，
∴3﹣t＝3（t﹣2），
∴．
综上所述：当∠EPQ＝∠ACB时，t的值为或．
24．【解答】解：（1）当n＝3时，直线l2的解析式为y＝﹣3x+5，
∵直线l1：y＝2x与直线l2：y＝﹣3x+5相交于点M，
∴，
解得，
∴点M的坐标为（1，2）；
（2）∵当点A与点M重合时，M是直线l1与l2的交点，
∴点A在直线l1：y＝2x上，
∵A点的横坐标为n，
∴A（n，2n），
将A（n，2n）代入y＝﹣3x+2n﹣1中，
得2n＝﹣3n+2n﹣1，
解得，
∴直线l2的解析式为；
（3）①如图，
∵点A是线l1上的动点，且横坐标为n，AB⊥x轴，
∴点B横坐标为n，
∵点B在直线l2：y＝﹣3x+2n﹣1上，
∴y＝﹣3n+2n﹣1＝﹣n﹣1，
∴点B（n，﹣n﹣1），
∵点B、C纵坐标相同，
∴，
∴，AB＝|2n﹣（﹣n﹣1）|＝|3n+1|，
在Rt△ABC中，由勾股定理得，
∵AD⊥l1，
∴AD解析式为，
联立，
解得，
∴，
∴，
∴，
故答案为：；
②n＝1或．
由①得，，
∵AC和CD为边作▱ACDE，S▱ACDE＝8，
∴AC•AD＝8，
∴，
整理得（3n+1）2＝16，
∴3n+1＝4或3n+1＝﹣4，
解得n＝1或．
A
B
C
A
（A，B）
（A，C）
B
（B，A）
（B，C）
C
（C，A）
（C，B）