2023-2024学年江苏省苏州市吴江区汾湖教育集团七年级（上）第一次段考数学试卷.

这是一份2023-2024学年江苏省苏州市吴江区汾湖教育集团七年级（上）第一次段考数学试卷.，共8页。试卷主要包含了10，5时，求点Q表示的数；，3 ④—7，5L等内容，欢迎下载使用。

2023.10
试卷分值：130分 考试用时：120分钟
一、单选题（每小题3分，共10个小题，共30分）
1．超市出售的某种品牌的面粉袋上，标有质量为（25±0.2）kg的字样，从中任意拿出两袋，它们的质量最多相差（ ）
A．0.2 kgB．0.3 kgC．0.4 kgD．50.4 kg
2．中国是最早采用正负数表示相反意义的量，并进行负数运算的国家．若零上10℃记作+10℃，则零下10℃可记作（ ）
A．10℃B．0℃C．-10 ℃D．-20℃
3．下列说法中，正确的是（ ）
A．正有理数和负有理数统称有理数B．正分数、零、负分数统称分数
C．零不是自然数，但它是有理数D．一个有理数不是整数就是分数
4．已知有理数，在数轴上的位置如图所示，则，，，从大到小的顺序为（ ）．
A．B．
C．D．
5．下面算式与的值相等的是（ ）
A．B．
C．D．
6．下列判断正确的是 ( )
A．若，则，中至少一个为零
B．若，则一定有，
C．若，则一定有，
D．若，且，则，
7．用“*”定义一种新运算：对于任何有理数a和b，规定，如，则的值为（ ）
A． B．8 C．4 D．
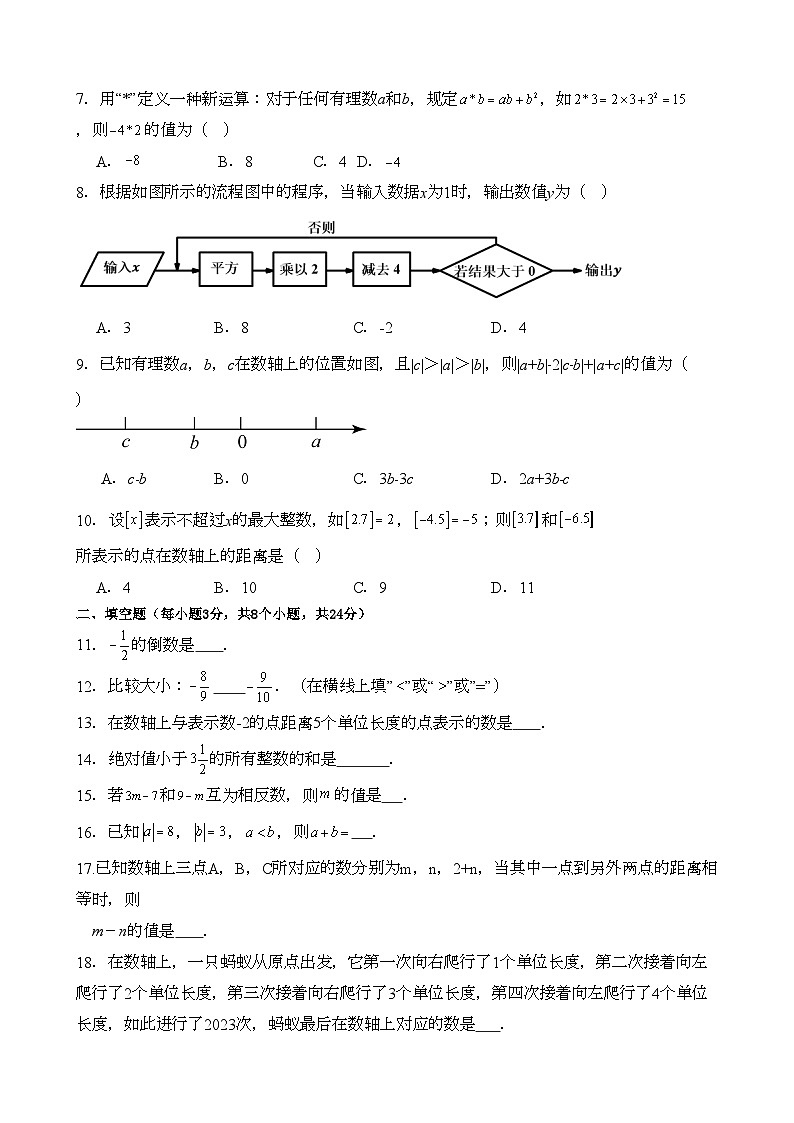
8．根据如图所示的流程图中的程序，当输入数据x为1时，输出数值y为（ ）
A．3B．8C．-2D．4
9．已知有理数a，b，c在数轴上的位置如图，且|c|＞|a|＞|b|，则|a+b|﹣2|c﹣b|+|a+c|的值为（ ）
A．c﹣bB．0C．3b﹣3cD．2a+3b﹣c
10．设表示不超过x的最大整数，如，；则和所表示的点在数轴上的距离是（ ）
A．4B．10C．9D．11
二、填空题（每小题3分，共8个小题，共24分）
11．的倒数是 ．
12．比较大小： ．（在横线上填””或“”或”=”）
13．在数轴上与表示数-2的点距离5个单位长度的点表示的数是 ．
14．绝对值小于的所有整数的和是 ．
15．若和互为相反数，则的值是 ．
16．已知，，，则 ．
17.已知数轴上三点A，B，C所对应的数分别为m，n，2+n，当其中一点到另外两点的距离相等时，则
m－n的值是 ．
18．在数轴上，一只蚂蚁从原点出发，它第一次向右爬行了1个单位长度，第二次接着向左爬行了2个单位长度，第三次接着向右爬行了3个单位长度，第四次接着向左爬行了4个单位长度，如此进行了2023次，蚂蚁最后在数轴上对应的数是 ．
三、解答题（共10个小题，共76分）
19．计算下列各题：（共4小题，每题4分，共16分）



（本题4分）在数轴上表示下列各数，并把它们用“＜”连接起来．
－（＋4）、1、－（－3.5）、0、－∣－2∣、
21．（本题6分）某高速公路养护小组，乘车沿南北向公路巡视维护，如果约定向北为正，向南为负，当天的行驶记录如下（单位：千米）
+17，﹣9，+7，﹣15，﹣3，+11，﹣6，﹣8，+5，+16
(1)养护小组最后到达的地方在出发点的哪个方向？距出发点多远？
(2)养护过程中，最远处离出发点有多远？
(3)若汽车耗油量为0.5升/千米，则这次养护共耗油多少升？
22．（本题6分）规定符号（a，b）表示a，b两个数中小的一个，符号[a，b]表示a，b两个数中大的一个，求下列式子的值．
（1）（﹣3，5）+[﹣5，3]； （2）（﹣2，﹣6）﹣[﹣9，（﹣4，﹣7）]．
23．（本题6分）已知，．
(1)当时，求的值；
(2)求的最大值．
24．（本题5分）若有理数x、y满足|x|=5，|y|=2，且|x+y|=x+y，求x﹣y的值.
25.（本题6分）．如图，在数轴上点A表示的数是8，若动点P从原点O出发，以2个单位/秒的速度向左运动，同时另一动点Q从点A出发，以4个单位/秒的速度也向左运动，到达原点后立即以原来的速度返回，向右运动，设运动的时间为t（秒）．
（1）当t＝0.5时，求点Q表示的数；
（2）当t＝2.5时，求点Q表示的数；
（3）当点Q到原点O的距离为4时，求点P表示的数．
26．（本题8分）数轴是一个非常重要的数学工具，它使数和数轴上的点建立起对应关系，揭示了数与点之间的内在联系，它是“数形结合”的基础．
例如：从“形”的角度看：可以理解为数轴上表示 3 和 1 的两点之间的
距离；可以理解为数轴上表示 3 与﹣1 的两点之间的距离．
从“数”的角度看：数轴上表示 4 和﹣3 的两点之间的距离可用代数式表示为： 4-（-3） ．
根据以上阅读材料探索下列问题：
(1)数轴上表示 3 和 9 的两点之间的距离是 ；数轴上表示 2 和﹣5 的两点之间的距离是 ；（直接写出最终结果）
(2)①若数轴上表示的数 x 和﹣2 的两点之间的距离是 4，则 x 的值为 ；
②若 x 为数轴上某动点表示的数，则式子的最小值为 ．
27．（本题9分）观察下列式子：；；；将这三个式子相加得到.
（1）猜想并写出： ．
（2）直接写出下列各式的计算结果：
① ．
② ．
（3）探究并计算：
28．（本题10分）已知数轴上两点A，B对应的数分别为﹣8和4，点P为数轴上一动点，若规定：点P到A的距离是点P到B的距离的3倍时，我们就称点P是关于A→B的“好点”．
（1）若点P到点A的距离等于点P到点B的距离时，求点P表示的数是多少?
（2）若点P以每秒1个单位的速度从原点O开始向右运动，当点P是关于A→B的“好点”时，求点P的运动时间.
（3）若点P在原点的左边（即点P对应的数为负数），且点P，A，B中，其中有一个点是关于其它任意两个点的“好点”，请直接写出所有符合条件的点P表示的数．初一数学参考答案：
1．C
2．C
3．D
4．C
5．C
6．A
7．D
8．D
9．A
10．B
11．—2
12．>
13．3或-7
14．0
15．—1
16．-5或-11
17．—2，1或者4
18．1012
19．①—29 ②—12 ③—4.3 ④—7
20．略
21．（1）北方15km处
（2）17km
（3）48.5L
（1）3或—3
（2）5
24．3或者7
25．（1）6 （2）2 （3）—2或者—6
26．(1)6，7；
(2)①－6或2；②4
27．（1） ；（2）①； ②；（3）
28.解：（1）∵数轴上两点A，B对应的数分别为﹣8和4，
∴AB＝4﹣（﹣8）＝12，
∵点P到点A、点B的距离相等，
∴P为AB的中点，
∴BP＝PA＝AB＝6，
∴点P表示的数是﹣2；
（2）根据题意可知：设点P运动的时间为t秒，
PA＝t+8，PB＝|4﹣t|，
∴t+8＝3|4﹣t|，
解得t＝1或t＝10，
所以点P的运动时间为1秒或10秒；
（3）根据题意可知：设点P表示的数为n，
PA＝n+8或﹣n﹣8，PB＝4﹣n，AB＝12，
分五种情况进行讨论：
①当点A是关于P→B的“好点”时，
|PA|＝3|AB|，
即﹣n﹣8＝36，解得n＝﹣44；
②当点A是关于B→P的“好点”时，
|AB|＝3|AP|，
即3（﹣n﹣8）＝12，解得n＝﹣12；
或3（n+8）＝12，解得n＝﹣4；
③当点P是关于A→B的“好点”时，
|PA|＝3|PB|，
即﹣n﹣8＝3（4﹣n）或n+8＝3（4﹣n），解得n＝10或1（不符合题意，舍去）；
④当点P是关于B→A的“好点”时，
|PB|＝3|AP|，
即4﹣n＝3（n+8），解得n＝﹣5；
或4﹣n＝3（﹣n﹣8），解得n＝﹣14；
⑤当点B是关于P→A的“好点”时，
|PB|＝3|AB|，
即4﹣n＝36，解得n＝﹣32．
综上所述：所有符合条件的点P表示的数是：﹣4，﹣5，﹣12，﹣14，﹣32，﹣44