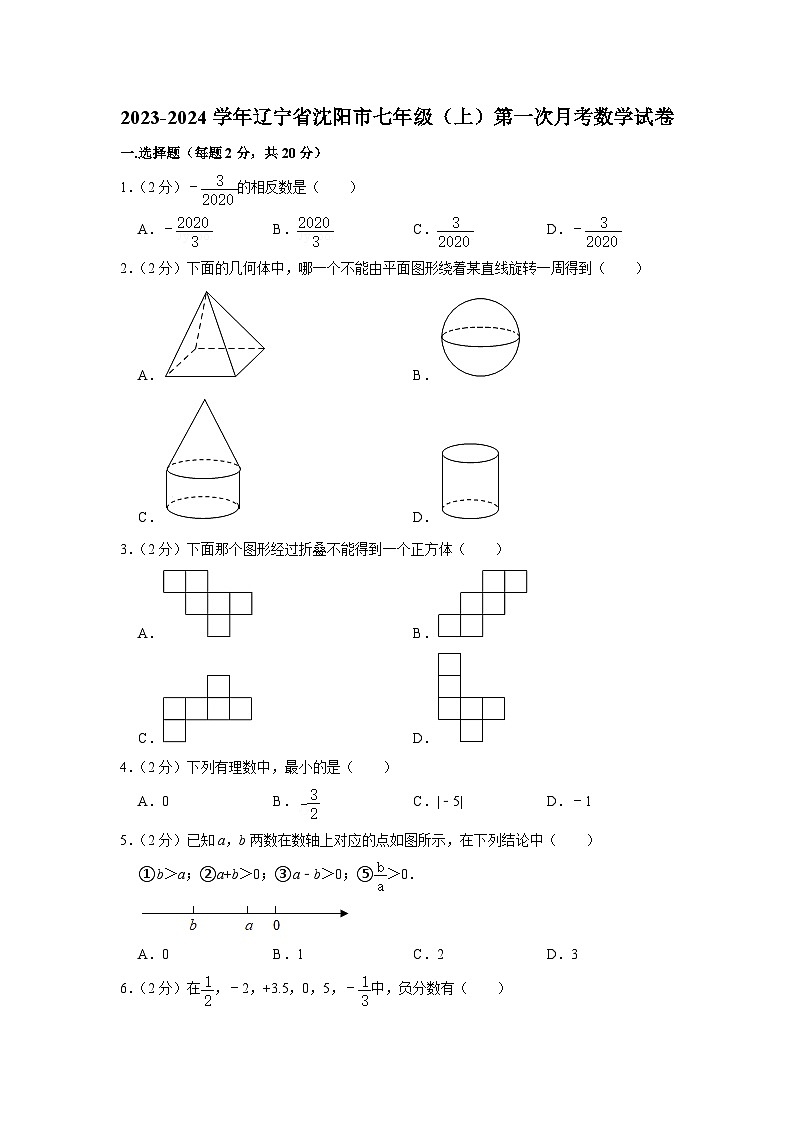
2023-2024学年辽宁省沈阳市七年级（上）第一次月考数学试卷

这是一份2023-2024学年辽宁省沈阳市七年级（上）第一次月考数学试卷，共14页。

A．﹣B．C．D．﹣
2．（2分）下面的几何体中，哪一个不能由平面图形绕着某直线旋转一周得到（ ）
A．B．
C．D．
3．（2分）下面那个图形经过折叠不能得到一个正方体（ ）
A．B．
C．D．
4．（2分）下列有理数中，最小的是（ ）
A．0B．C．|﹣5|D．﹣1
5．（2分）已知a，b两数在数轴上对应的点如图所示，在下列结论中（ ）
①b＞a；②a+b＞0；③a﹣b＞0；⑤＞0．
A．0B．1C．2D．3
6．（2分）在，﹣2，+3.5，0，5，﹣中，负分数有（ ）
A．1个B．2个C．3个D．4个
7．（2分）若|m|＝2，|n|＝3，且m＞n（ ）
A．﹣1B．﹣5C．1或﹣5D．﹣1或﹣5
8．（2分）下列说法：①可以在数轴上找到表示的点；②在数轴上离原点越近的点所对应的数越小，积的符号由负因数的个数决定；④有理数可分为正有理数和负有理数，错误的有（ ）
A．2个B．3个C．4个D．5个
9．（2分）用一个平面去截一个三棱柱，截面边数最多为（ ）条．
A．3B．4C．5D．6
10．（2分）正方形ABCD在数轴上的位置如图所示，点D，A对应的数分别为0，1，翻转1次后，点B所对应的数为2，数轴上数2023所对应的点是（ ）
A．AB．BC．CD．D
二.填空题（每题3分，共24分）
11．（3分）小明向南走200米记作+200米，则向北走40米记作 米．
12．（3分）比较大小：﹣（﹣1 ） ﹣|﹣1.35|．（填“＜”、“＞”或“＝”）
13．（3分）将一张纸对折1次可裁2张，对折2次可裁4张，对折6次可裁 张．
14．（3分）一个棱柱有7个面，它的底面边长都是4cm，侧棱长3cm cm2．
15．（3分）如果x＜y＜0，那么+化简结果为 ．
16．（3分）纽约与北京的时差为﹣13小时，李伯伯在北京乘坐早晨9：00的航班飞行约20小时到达纽约，则李伯伯到达纽约时间是 时．
17．（3分）定义：对于任何数a，符号[a]表示不大于a的最大整数，例如：[5.7]＝5，则[﹣4.2]+[1.8]﹣[﹣2.3]＝ ．
18．（3分）实际测量一座山的高度时，可在若干个观测点中测量每两个相邻可视观测点的相对高度然后用这些相对高度计算出山的高度．下表是某次测量数据的部分记录（用A﹣C表示观测点A相对观测点C的高度）；
根据这次测量的数据，可得观测点A相对观测点B的高度是 米．
三.解答题（共56分）
19．（6分）在数轴上分别用A，B，C，D，E把有理数0，+（﹣3.5），|﹣4|，（﹣1）2，﹣（﹣5）表示出来，并用“＜”把它们连接起来．
20．（8分）一个几何体是由若干个棱长为2cm的小正方体搭成的，从左面、上面看到的几何体的形状图如图所示．
（1）该几何体最少由 个小立方体组成，最多由 个小立方体组成．
（2）将该几何体的形状固定好．
①画出该几何体体积最大时的主视图；
②体积最大时的几何体表面积（包括底面）为 ．
​
21．（18分）计算：
（1）12﹣（﹣18）+（﹣9）﹣15；
（2）；
（3）（﹣5）×6+（﹣125）÷（﹣5）；
（4）；
（5）（要求简算）；
（6）﹣10+8÷（﹣2）2﹣（﹣4）×（﹣3）．
22．（8分）某个体儿童服装店老板以每件32元的价格购进30件连衣裙，针对不同的顾客，30件连衣裙的售价不完全相同，将超过的钱数记为正，不足的钱数记为负
（1）总进价是 元．
（2）在销售过程中①最低售价为每件 元；②最高获利为每件 元．
（3）该服装店在售完这30件连衣裙后，赚了多少钱？
23．（8分）出租车司机小王某天下午营运全是在南北走向的公路上进行的．如果向南记作“+”，向北记作“﹣”，他这天下午行车情况如下：（单位：千米）
﹣2，+5，﹣8，+6，﹣6．
（1）小王将最后一名乘客送到目的地时，在下午出车的出发地的什么方向？距下午出车的出发地多远？
（2）若出租车每公里耗油0.3升，求小王回到出发地共耗油多少升？
（3）若规定每趟车的起步价是10元，且每趟车3千米以内（含3千米）只收起步价，除收起步价外，超过的每千米（不足1千米按1千米计算），小王今天是收入是多少元？
24．（8分）阅读理解：若A、B、C为数轴上三点，若点C到A的距离是点C到B的距离的2倍，我们称点C是【A，我们称点C是【B，A】的妙点．
（1）如图1，点A表示的数为﹣1，点B表示的数为2．表示0的点D到点A的距离是1，那么点D 【A，B】的妙点，点D 【B，A】的妙点．（请在横线上填是或不是）
（2）如图2，M、N为数轴上两点，点M所表示的数为﹣2，N】的妙点所表示的数是 ．
（3）如图3，A、B为数轴上两点，点A所表示的数为﹣20，以3个单位每秒的速度向左运动，到达点A停止．当经过 秒时，P、A和B中恰有一个点为其余两点的妙点．
参考答案与试题解析
一.选择题（每题2分，共20分）
1．【分析】直接利用相反数的定义得出答案．
【解答】解：﹣的相反数是：．
故选：C．
【点评】此题主要考查了相反数，正确把握相反数的定义是解题关键．
2．【分析】根据棱锥、圆柱、圆锥、球的形体特征结合旋转的性质得到答案．
【解答】解：由平面图形绕着某直线旋转一周得到几何体一定有曲面，而四棱锥的面都是平面，
所以四棱锥不能由平面图形绕着某直线旋转一周得到，
故选：A．
【点评】本题考查点、线、面、体，掌握面动成体是解决问题的关键．
3．【分析】根据正方体展开图的常见形式作答即可．
【解答】解：由展开图可知：选项A、B、C能围成正方体；
选项D围成几何体时，有两个面重合，符合题意．
故选：D．
【点评】本题考查了展开图折叠成几何体．能组成正方体的“一，四，一”“三，三”“二，二，二”“一，三，二”的基本形态要记牢．
4．【分析】计算出|﹣5|＝5，然后利用正数，负数和0的大小关系进行比较．
【解答】解：∵|﹣5|＝5，
∴7＞0＞﹣1＞﹣，
故选：B．
【点评】本题考查了绝对值的意义和有理数的大小比较，必须熟练掌握才能正确判断．
5．【分析】利用有理数的加减乘除法则判断即可．
【解答】解：根据数轴上点的位置得：b＜a＜0，
则b＜a，a+b＜0，ab＞4，，
故③⑤正确，正确的个数是2．
故选：C．
【点评】此题考查了有理数的加、减、乘、除法，以及数轴，熟练掌握运算法则是解本题的关键．
6．【分析】据分母不为1的数是分数，可得分数，再根据小于0的分数是负分数，可得负分数．
【解答】解：在，﹣6，0，﹣0.7，5，﹣中，
负分数有﹣0.7，﹣，共有2个，
故选：B．
【点评】本题考查了有理数．先判断分数，再判断负分数，是解题的关键．
7．【分析】根据绝对值的定义求出m，n的值，根据m＞n分两种情况分别计算即可．
【解答】解：∵|m|＝2，|n|＝3，
∴m＝±2，n＝±3，
∵m＞n，
∴当m＝2，n＝﹣6时；
当m＝﹣2，n＝﹣3时；
故选：D．
【点评】本题考查了有理数的加法，绝对值，体现了分类讨论的数学思想，分两种情况分别计算是解题的关键，不要漏解．
8．【分析】根据数轴、绝对值、有理数的分类和有理数的乘法法则，逐个判断得结论．
【解答】解：在数轴上可以找到表示的点；在正半轴上，在负半轴上，故②错误；
几个非3的有理数相乘，积的符号由负因数的个数确定，故③错误、0和负有理数；
正数的绝对值等于它本身，故⑤正确．
故选：B．
【点评】本题考查了有理数的分类、绝对值和有理数乘法的符号法则．掌握有理数的分类和乘法的符号法则是解决本题的关键．
9．【分析】根据截一个几何体，截面的边数与几何体面数的关系进行判断即可．
【解答】解：三棱柱有5个面，若截面均经过这5个面，
故选：C．
【点评】本题考查截一个几何体，理解“截面的边数与几何体面数的关系”是正确解答的关键．
10．【分析】通过题意得到4个数为一个循环，由2023÷4＝505……3．
【解答】解：由题意可知，
D初始位置对应的数字为0，
D下一个对应得到数字是4，
再下一个对应的数字是6，
∴4个数为一个循环，
旋转2020次后，2020÷4＝505，
∴数轴上数2020所对应的点是D，
∴数轴上数2021所对应的点是A．
∴数轴上数2022所对应的点是B．
∴数轴上数2023所对应的点是C．
故选：C．
【点评】本题考查实数数轴，能够确定多少个数为一个循环是解答本题的关键．
二.填空题（每题3分，共24分）
11．【分析】正数和负数是一组具有相反意义的量，据此即可求得答案．
【解答】解：向南走200米记作+200米，则向北走40米记作﹣40米，
故答案为：﹣40．
【点评】本题考查正数和负数，熟练掌握正数和负数的实际意义是解题的关键．
12．【分析】分别化简后，再根据有理数大小的比较方法进行解答即可．
【解答】解：﹣（﹣）＝1.6，
由于5.6＞﹣1.35，
所以﹣（﹣7 ）＞﹣|﹣3.35|．
故答案为：＞．
【点评】本题考查绝对值，相反数，理解绝对值、相反数的定义是正确解答的关键．
13．【分析】将一张纸对折1次可裁2张，即21张，对折2次可裁4张，即22张，对折3次可裁8张，即23张，...，对折6次可裁26张，由此解答即可．
【解答】解：由分析可知，对折6次可裁22＝64（张），
故答案为：64．
【点评】本题是一道找规律的题目，对于找规律的题目首先应找出哪部分发生了变化，是按照什么规律变化的．
14．【分析】根据侧面积公式求解．
【解答】解：由题意得：该棱柱是五棱柱，
∴侧面积的和为：4×5×2＝60（cm2），
故答案为：60．
【点评】本题考查了几何体的表面积，理解侧面展开图是解题的关键．
15．【分析】先根据x＜y＜0判断出xy的符号，再根据绝对值的性质去掉绝对值符号，把原式进行化简即可．
【解答】解：∵x＜y＜0，
∴xy＞0，
∴|xy|＝xy，
∴原式＝+＝﹣5+1＝0．
故答案为：7．
【点评】本题考查的是分式的化简求值，熟知分式混合运算的法则是解答此题的关键．
16．【分析】根据正数和负数的实际意义列式计算即可．
【解答】解：9+20﹣24﹣13+24＝16（时），
即李伯伯到达纽约时间是16时，
故答案为：16．
【点评】本题考查正数和负数及有理数运算的实际应用，结合已知条件列得正确的算式是解题的关键．
17．【分析】先根据符号[a]表示不大于a的最大整数可得[﹣4.2]＝﹣5，[1.8]＝1，[﹣2.3]＝﹣3，再根据有理数的加减法法则计算即可．
【解答】解：由题意可得：
[﹣4.2]+[5.8]﹣[﹣2.2]
＝﹣5+1﹣（﹣4）
＝﹣4+3
＝﹣4．
故答案为：﹣1．
【点评】本题主要考查了有理数的大小比较以及有理数的加减法，解题的关键是掌握新定义．
18．【分析】根据正数和负数的实际意义列式计算即可．
【解答】解：100+80﹣（﹣60）﹣50﹣（﹣70）﹣30
＝180+60﹣50+70﹣30
＝230（米），
即观测点A相对观测点B的高度是230米，
故答案为：230．
【点评】本题考查正数和负数及有理数运算的实际应用，结合已知条件列得正确的算式是解题的关键．
三.解答题（共56分）
19．【分析】先将各数化简后在数轴上分别用A，B，C，D，E表示出来，再利用数轴上右边的总比左边的大用“＜”吧它们连接起来即可．
【解答】解：∵+（﹣3.5）＝﹣2.5，|﹣4|＝42＝1，﹣（﹣3）＝5，
∴在数轴上分别用A，B，C，D，E把有理数0，|﹣2|2，﹣（﹣5）表示出来如下：
用“＜”把它们连接起来：
+（﹣8.5）＜0＜（﹣4）2＜|﹣4|＜﹣（﹣8）．
【点评】本题主要考查了有理数的大小的比较，数轴，利用数轴上的Ian表示出各数是解题的关键．
20．【分析】（1）根据左视图，俯视图判断即可；
（2）①画出几何体体积最大时的主视图即可；
①分6个方向，分别计算小正方形的个数即可．
【解答】解：（1）该几何体最少由9个小立方体组成，最多由13个小立方体组成．
故答案为：9，13；
（2）出该几何体体积最大时的主视图如图所示：
②体积最大时的几何体表面积（包括底面）为＝3+3+3+2+3+3+3+6+6+6＝42．
故答案为：42．
【点评】本题考查作图﹣三视图，几何体的表面积，三视图判断几何体等知识，解题的关键是理解题意，灵活运用所学知识解决问题．
21．【分析】（1）化简符号再计算；
（2）化简符号，再通分计算；
（3）先乘除，再加减；
（4）把除化为乘，再用乘法分配律；
（5）把﹣99变形，再用乘法分配律；
（6）先乘方，再乘除，最后加减．
【解答】解：（1）原式＝12+18﹣9﹣15
＝6；
（2）原式＝﹣+﹣
＝﹣+﹣
＝；
（3）原式＝﹣30+25
＝﹣5；
（4）原式＝×（﹣18）﹣×（﹣18）
＝﹣3++
＝﹣2；
（5）原式＝（﹣100+）×34
＝﹣100×34+×34
＝﹣3400+3
＝﹣3396；
（6）原式＝﹣10+8÷4﹣12
＝﹣10+3﹣12
＝﹣20．
【点评】本题考查有理数的混合运算，解题的关键是掌握有理数相关的运算法则．
22．【分析】（1）根据“总价＝单价×数量”列式计算解答即可；
（2）根据正数、负数的意义，求出结果；
（3）分别求出按照不同价格售出的利润，再求和即可．
【解答】解：（1）32×30＝960（元），
即总进价是960元，
故答案为：960；
（2）在销售过程中最低售价为每件：40﹣6＝34（元）；最高获利为每件：40+5﹣32＝13（元），
故答案为：34；13；
（3）4×（40+5）+9×（40+8）+3×（40+1）+4×（40﹣2）+4×（40﹣3）+5×（40﹣6）﹣960
＝180+378+123+190+144+170﹣960
＝225（元），
答：赚了225元．
【点评】本题考查正数和负数以及有理数的混合运算；理解正数与负数在实际应用中的意义是解题的关键．
23．【分析】（1）根据有理数的加法进行计算即可得到答案；
（2）将这些数的绝对值相加，求出总路程，再根据出租车每公里耗油0.3升，可得答案；
（3）根据行车记录和收费方法列出算式，计算即可得解．
【解答】解：（1）﹣2+5﹣5﹣3+6﹣8＝﹣8（千米），
∴小王将最后一名乘客送到目的地时，小王在下午出车的出发地的北方．
（2）|﹣2|+|8|+|﹣8|+|﹣3|+|2|+|﹣6|＝30（千米），
30×0.7＝9（升），
8×5.3＝2.3（升），
9+2.8＝11.4（升），
∴小王回到出发地共耗油11.4升．
（3）根据出租车收费标准，可知小王今天的收入是10+[10+（7﹣3）×4]+[10+（3﹣3）×4]+10+[10+（8﹣3）×4]+[10+（5﹣3）×4]＝112（元），
∴小王今天的收入是112元．
【点评】本题考查有理数的加法运算，有理数的乘法运算，解题的关键是掌握有理数的运算法则．
24．【分析】（1）求出DB＝2DA，可知点D不是【A，B】的妙点，点D是【B，A】的妙点；
（2）设【M，N】的妙点所表示的数是x，可得：|x﹣（﹣2）|＝2|x﹣4|，即可解得答案；
（3）设P运动时间为t秒，可知t≤20，分六种情况分别列出方程，可解得答案．
【解答】解：（1）∵DA＝1，DB＝2，
∴DB＝7DA，
∴点D不是【A，B】的妙点，A】的妙点，
故答案为：不是，是；
（2）设【M，N】的妙点所表示的数是x，
根据题意得：|x﹣（﹣2）|＝2|x﹣6|，
解得x＝2或x＝10，
∴【M，N】的妙点所表示的数是2或10，
故答案为：5或10；
（3）设P运动时间为t秒，则P表示的数为40﹣3t，
∵到达点A停止，
∴40﹣3t≥﹣20，
∴t≤20，
①P为【A，B】的妙点时，
解得t＝或t＝﹣20（舍去）；
②P为【B，A】的妙点时，
解得t＝或t＝40（大于20；
③A为【P，B】的妙点时
解得t＝﹣20（舍去）或t＝60（大于20，舍去）；
④A为【B，P】的妙点时，
解得t＝10或t＝30（大于20，舍去）；
⑤B为【P，A】的妙点时，
解得t＝40（大于20，舍去）；
⑥B为【A，P】的妙点时
解得t＝10；
综上所述，t的值为或，
故答案为：或或10．
【点评】本题考查一元一次方程的应用，涉及新定义，解题的关键是读懂题意，能分类列出方程解决问题．A﹣C
C﹣D
E﹣D
F﹣E
G﹣F
B﹣G
100米
80米
﹣60米
50米
﹣70米
30米
售出数量（件）
4
9
3
5
4
5
售价（元）
+5
+2
+1
﹣2
﹣4
﹣6