2023-2024学年黑龙江省哈尔滨九年级（上）月考数学试卷（10月份）（五四学制）

这是一份2023-2024学年黑龙江省哈尔滨九年级（上）月考数学试卷（10月份）（五四学制），共26页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

1．（3分）中国是最早采用正负数表示相反意义的量、并进行负数运算的国家，若收入500元记作+500元，则支出137元记作（ ）
A．+137元B．﹣137元C．0元D．﹣174元
2．（3分）下列各式运算结果为a5的是（ ）
A．a2+a3B．a2a3C．（a2）3D．a10÷a2
3．（3分）下列图形中，是中心对称图形但不是轴对称图形的是（ ）
A．B．
C．D．
4．（3分）在平面直角坐标系中，点P（﹣20，a）与点Q（b，13），则a+b的值为（ ）
A．33B．﹣33C．﹣7D．7
5．（3分）如图，在Rt△ABC中，∠C＝90°，AB＝5，则csA的值是（ ）
A．B．C．D．
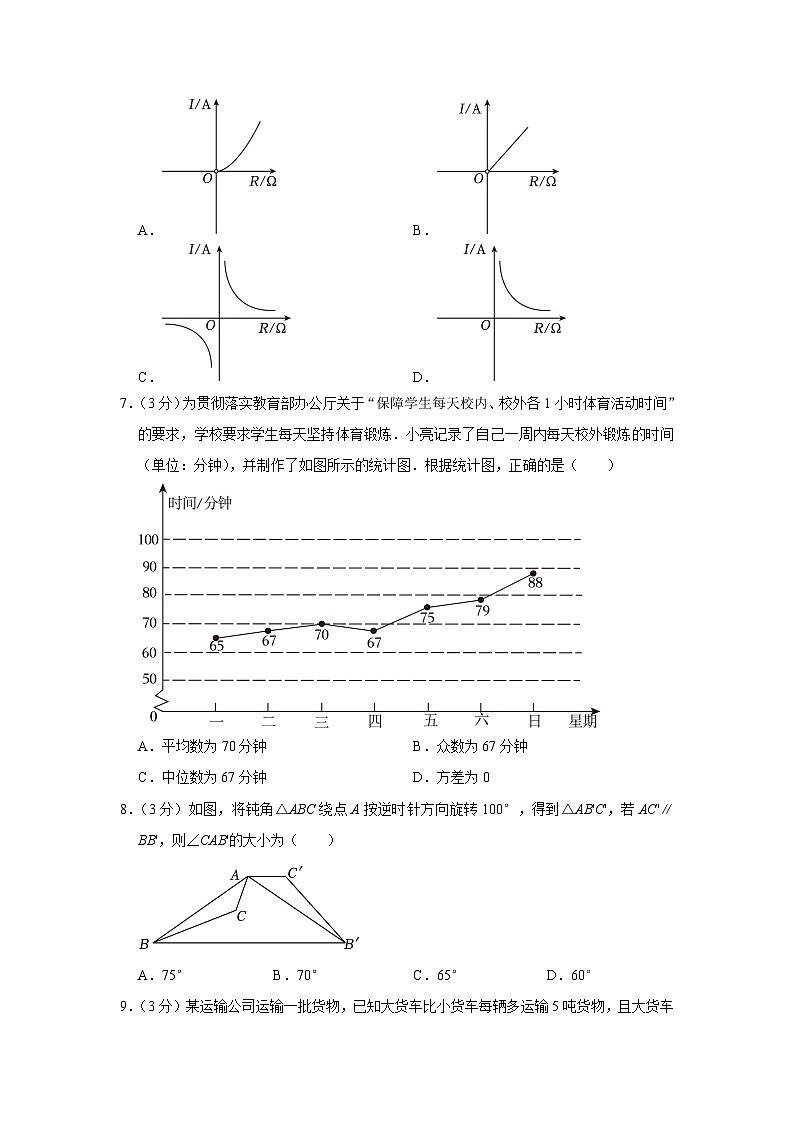
6．（3分）已知蓄电池的电压U为定值，使用蓄电池时，电流I（单位：A）（单位：Ω）是反比例函数关系（I＝）．下列反映电流I与电阻R之间函数关系的图象大致是（ ）
A．B．
C．D．
7．（3分）为贯彻落实教育部办公厅关于“保障学生每天校内、校外各1小时体育活动时间”的要求，学校要求学生每天坚持体育锻炼．小亮记录了自己一周内每天校外锻炼的时间（单位：分钟），并制作了如图所示的统计图．​根据统计图，正确的是（ ）
A．平均数为70分钟B．众数为67分钟
C．中位数为67分钟D．方差为0
8．（3分）如图，将钝角△ABC绕点A按逆时针方向旋转100°，得到△AB'C'，若AC'∥BB'，则∠CAB'的大小为（ ）
A．75°B．70°C．65°D．60°
9．（3分）某运输公司运输一批货物，已知大货车比小货车每辆多运输5吨货物，且大货车运输75吨货物所用车辆数与小货车运输50吨货物所用车辆数相同，则所列方程正确的是（ ）
A．＝B．＝C．＝D．＝
10．（3分）如图，点E在正方形ABCD的对角线AC上，EF⊥AB于点F，交边BC于点M，交边AB的延长线于点G．若AF＝2，则MG＝（ ）
A．2B．C．+1D．
二、填空题（每题3分，共30分）
11．（3分）据共青团中央2023年5月3日发布的中国共青团团内统计公报，截至2022年12月底，全国共有共青团员7358万．数据7358万用科学记数法表示 ．
12．（3分）在函数y＝中，自变量x的取值范围是 ．
13．（3分）把多项式8xy2﹣2x分解因式的结果是 ．
14．（3分）如图，∠AOB＝60°，点C在OB上，P为∠AOB内一点．根据图中尺规作图痕迹推断，点P到OA的距离为 ．
15．（3分）如图，一条公路的转弯处是一段圆弧（），点O是这段弧所在圆的圆心一点，OB⊥AC于D．若米，则的⊙O的半径长为 米．
16．（3分）如图1，在Rt△ABC中，动点P从A点运动到B点再到C点后停止，其中BP长与运动时间t（单位：s）的关系如图2 ．
17．（3分）综合实践课上，航模小组用航拍无人机进行测高实践．如图，无人机从地面CD的中点A处竖直上升30米到达B处，尚美楼顶部F的俯角为30°，已知博雅楼高度CE为15米 米．（结果保留根号）
18．（3分）在菱形ABCD中，∠ABC＝60°，BD＝，，将射线CE绕点C旋转60°，得到的射线CF交AD于点F ．
19．（3分）找规律：观察算式：13＝1；13+23＝9；13+23+33＝36；13+23+33+43＝100；…，按规律填空：13+23+33+43+…+103＝ ．
20．（3分）如图，四边形ACBE中，∠ACB＝90°，D在AC边上，且∠AED+∠AEB＝180°，，则AD的长为 ．
三、解答题（21、22题8分，23题9分，24、25题10分，26题15分）
21．（8分）先化简，再求代数式：的值
22．（8分）如图是8×6的正方形网格，已知△ABC，请按下列要求完成作图．（要求保留作图痕迹，不要求写作法和结论）
（1）将△ABC绕C点按顺时针方向旋转90°，得到△A1B1C1，请在图中作出△A1B1C1；
（2）在图中，以∠B为公共角，仅用无刻度直尺在线段AB，Q，使△BPQ与△BAC相似但不全等．
23．（9分）一次函数y1＝kx+b的图象与反比例函数y2＝的图象相交于A，B两点（1，6），点B的纵坐标是﹣2．
​（1）求一次函数和反比例函数的解析式；
（2）C为x轴正半轴上一点，连接AC，BC．若△ABC的面积是16
24．（10分）（一）如图1，四边形ABCD为正方形，点E在边BC上，FG⊥BC 交BC延长线于点G，AE＝EF，请直接写出线段AC、CE、FG之间的数量关系 ；
（二）如图2，四边形ABCD为菱形，∠B＝60°，点F在边CD上，AE＝EF；
（1）直接写出AC、CE、FG之间的数量关系 ；
（2）请用两种方法证明（1）中结论．
25．（10分）某商场计划购进一批篮球和足球，其中篮球的单价比足球的单价多30元，已知用360元购进的足球和用480元购进的篮球数量相等．
（1）问篮球和足球的单价各是多少元？
（2）若篮球售价为每个150元，足球售价为每个110元，商场售出足球的数量比篮球数量的三分之一还多10个，问篮球最少要卖多少个？
（3）若篮球售价为每个150元，足球售价为每个110元，商场计划用不超过10350元购进两种球共100个，问商场有几种进货方案？哪种方案商场获利最大？
26．（15分）已知抛物线y＝x2+bx+c顶点D．
（1）求b、c的值；
（2）点P是第一象限对称轴右侧抛物上一点，点P的横坐标为t，过点P作y轴的平行线交直线CB于点Q，求d与t之间的函数关系式（不用写出自变量t的取值范围）；
（3）在（2）的条件下，以点P为圆心的⊙P交抛物线的对称轴于点M、N（点M在点N的上方），⊙P半径为，求点P的坐标；
（4）在（2）的条件下，点P在第一象限对称轴右侧抛物线上（点M在点N的上方），过点P作y轴垂线，交抛物线于另一点E，连接PN并延长交ED于点T，若PT⊥ED于点T，求点Q的坐标．
参考答案与试题解析
一、选择题（每题3分，共30分）
1．【分析】正数和负数是一组具有相反意义的量，据此即可求得答案．
【解答】解：收入500元记作+500元，则支出137元记作﹣137元，
故选：B．
【点评】本题考查正数和负数，理解正负的相对性，明确什么是一对具有相反意义的量是解题的关键．
2．【分析】根据幂的乘方和积的乘方的运算方法，同底数幂的乘法、除法的运算方法，逐项判断即可．
【解答】解：∵a2+a3≠a2，
∴选项A不符合题意；
∵a2a3＝a6，
∴选项B符合题意；
∵（a2）3＝a2≠a5，
∴选项C不符合题意；
∵a10÷a2＝a3≠a5，
∴选项D不符合题意．
故选：B．
【点评】此题主要考查了幂的乘方和积的乘方的运算方法，同底数幂的乘法、除法的运算方法，解答此题的关键是要明确：（1）（am）n＝amn（m，n是正整数），（ab）n＝anbn（n是正整数）；（2）同底数幂相乘，底数不变，指数相加；（3）同底数幂相除，底数不变，指数相减．
3．【分析】根据中心对称图形与轴对称图形的概念判断．
【解答】解：A、既不是轴对称图形，不符合题意；
B、既是轴对称图形，不符合题意；
C、是轴对称图形，不符合题意；
D、不是轴对称图形，符合题意；
故选：D．
【点评】本题考查的是中心对称图形与轴对称图形的概念，轴对称图形的关键是寻找对称轴，图形两部分折叠后可重合，中心对称图形是要寻找对称中心，旋转180度后两部分重合．
4．【分析】先根据关于原点对称的点的坐标特点：横坐标与纵坐标都互为相反数，求出a与b的值，再代入计算即可．
【解答】解：∵点P（﹣20，a）与点Q（b，
∴a＝﹣13，b＝20，
∴a+b＝﹣13+20＝7．
故选：D．
【点评】本题主要考查了关于原点对称的点的坐标，解决本题的关键是掌握好对称点的坐标规律：关于原点对称的点，横坐标与纵坐标都互为相反数．
5．【分析】根据余弦的定义计算即可．
【解答】解：在Rt△ABC中，csA＝＝，
故选：B．
【点评】本题考查的是锐角三角函数的定义，掌握锐角A的邻边b与斜边c的比叫做∠A的余弦是解题的关键．
6．【分析】根据题意得到电流I（单位：A）与电阻R（单位：Ω）是反比例函数关系（I＝），于是得到结论．
【解答】解：∵电流I（单位：A）与电阻R（单位：Ω）是反比例函数关系（I＝），R、I均大于0，
∴反映电流I与电阻R之间函数关系的图象大致是D选项，
故选：D．
【点评】本题考查反比例函数的应用，解题的关键是学会利用图象信息解决问题，属于中考常考题型．
7．【分析】根据折线图分别求出平均数、众数、中位数和方差进行判断即可．
【解答】解：根据折线图小亮该周每天校外锻炼时间为：65、67、67、79，
A．平均数是，故选项错误；
B．这组数的众数是67（分钟），符合题意；
C．将这组数由小到大排列为：65、67、75、88，故选项错误；
D．这组方差为：S2＝×[（65﹣73）2+（67﹣73）3+（70﹣73）2+（67﹣73）2+（75﹣73）4+（79﹣73）2+（88﹣73）2]≈58.57，故选项错误；
故选：B．
【点评】本题考查了折线图，平均数、众数、中位数和方差的计算，掌握折线图的特点，平均数、众数、中位数和方差的计算方法是关键．
8．【分析】根据旋转的性质得到∠BAB′＝∠CAC′＝100°，AB＝AB′，根据等腰三角形的性质易得∠AB′B＝40°，再根据平行线的性质即可得∠C′AB′＝∠AB′B＝40°，即可得解．
【解答】解：∵将△ABC绕点A按逆时针方向旋转100°得到△AB′C′，
∴∠BAB′＝∠CAC′＝100°，AB＝AB′，
∴∠AB′B＝（180°﹣100°）＝40°，
∵AC′∥BB′，
∴∠C′AB′＝∠AB′B＝40°，
∴∠CAB＝∠C′AB′＝40°，
∴∠CAB'＝100°﹣∠CAB＝100°﹣40°＝60°，
故选：D．
【点评】本题考查了旋转的性质：旋转前后两图形全等；对应点到旋转中心的距离相等；对应点与旋转中心的连线段的夹角等于旋转角．
9．【分析】由每辆大货车的货运量是x吨，则每辆小货车的货运量是（x﹣5）吨，根据用大货车运送75吨货物所需车辆数与小货车运送50吨货物所需车辆数相同，即可得出关于x的分式方程．
【解答】解：∵每辆大货车的货运量是x吨，
∴每辆小货车的货运量是（ x﹣5）吨，
依题意得：＝．
故选：B．
【点评】本题考查了由实际问题抽象出分式方程，找准等量关系，正确列出分式方程是解题的关键．
10．【分析】根据相似三角形的判定结合正方形的性质证得△AEF∽△ACB，求得AC＝3，根据相似三角形的性质求得AE＝2，CE＝，证得△ADE∽△CME，根据相似三角形的性质得到CM＝＝BM，证得△CDM≌△BGM，求出BG，根据勾股定理即可求出MG．
【解答】解：∵四边形ABCD是正方形，AF＝2，
∴CD＝AD＝AB＝BC＝3，∠ADC＝∠DAB＝∠ABC＝90°，AD∥BC，
∴AC＝＝3，
∵EF⊥AB，
∴EF∥BC，
∴△AEF∽△ACB，
∴＝，
∴＝，
∴EF＝2，
∴AE＝＝2，
∴CE＝AC﹣AE＝，
∵AD∥CM，
∴△ADE∽△CME，
∴＝，
∴＝＝2，
∴CM＝＝BM，
在△CDM和△BGM中，
，
∴△CDM≌△BGM（SAS），
∴CD＝BG＝3，
∴MG＝＝＝．
故选：B．
【点评】本题考查了正方形的性质，全等三角形的判定和性质，勾股定理，相似三角形的判定和性质，熟练掌握正方形的性质是解题的关键．
二、填空题（每题3分，共30分）
11．【分析】将一个数表示成a×10n的形式，其中1≤|a|＜10，n为整数，这种记数方法叫做科学记数法，据此即可求得答案．
【解答】解：7358万＝73580000＝7.358×107，
故答案为：4.358×107．
【点评】本题考查科学记数法表示较大的数，熟练掌握其定义是解题的关键．
12．【分析】根据分式有意义的条件：分母不等于0即可求解．
【解答】解：根据题意得：4﹣2x≠3，解得x≠2．
故答案为：x≠2．
【点评】本题考查了函数自变量的取值范围，初中范围内一般要考虑三种情况：1、分母不等于0；2、二次根式被开方数是非负数；3、0的0次幂或负指数次幂无意义．
13．【分析】提公因式后利用平方差公式因式分解即可．
【解答】解：原式＝2x（4y8﹣1）＝2x（3y+1）（2y﹣5），
故答案为：2x（2y+2）（2y﹣1）．
【点评】本题考查提公因式法及公式法因式分解，熟练掌握因式分解的方法是解题的关键．
14．【分析】由作图知PE垂直平分OC，CO平分∠AOB，根据线段垂直平分线的性质得到OE＝OC＝，∠PEO＝90°，根据角平分线的定义得到∠POE＝∠AOC＝＝30°，根据三角函数的定义得到EP＝OE×tan30°＝，根据角平分线的性质即可得到结论．
【解答】解：由作图知PE垂直平分OC，OP平分∠AOB，
∴OE＝OC＝，
∵∠AOB＝60°，
∴∠POE＝∠AOP＝＝30°，
∴EP＝OE×tan30°＝，
∵PO平分∠AOB，
∴点P到OA的距离＝PE＝1．
故答案为：7．
【点评】此题主要考查了作图﹣基本作图．以及角平分线的性质，关键是掌握角平分线的性质．
15．【分析】设圆的半径是r米，由垂径定理推出AD＝AC＝150（米），由勾股定理得到r2＝（r﹣150）2+，求出r＝300，即可得到⊙O的半径长为300米．
【解答】解：设圆的半径是r米，则OD＝（r﹣150）米，
∵OB⊥AC，
∴AD＝AC＝＝150，
∵OA2＝OD2+AD6，
∴r2＝（r﹣150）2+，
∴r＝300，
∴⊙O的半径长为300米．
故答案为：300．
【点评】本题考查垂径定理，勾股定理，关键是由以上知识点列出关于圆半径的方程．
16．【分析】根据图象可知t＝0时，点P与点A重合，得到AB＝15，进而求出点P从点A运动到点所需的时间，进而得到点P从点B运动到点C的时间，求出BC的长，再利用勾股定理求出AC即可．
【解答】解：由图象可知：t＝0时，点P与点A重合，
∴AB＝15，
∴点P从点A运动到点B所需的时间为15÷2＝2.5（s）；
∴点P从点B运动到点C的时间为11.5﹣8.5＝4（s），
∴BC＝6×4＝8；
在Rt△ABC中，由勾股定理可得AC＝17；
故答案为：17．
【点评】本题考查动点的函数图象，勾股定理．从函数图象中有效的获取信息，求出AB，BC的长是解题的关键．
17．【分析】过点E作EM⊥过点B的水平线于M，过点F作FN⊥过点B的水平线于N，先求出EM的长，在Rt△EBM中求出BM的长，然后求出BN的长，在Rt△FBN中求出FN的长，即可求出DF的长．
【解答】解：如图，过点E作EM⊥过点B的水平线于M，
由题意可知CM＝DN＝AB＝30米，
又∵CE＝15米，
∴EM＝15米，
在Rt△EBM中，∠EBM＝45°，
∴BM＝EM＝15米，
又∵A是CD的中点，
∴BN＝AD＝AC＝BM＝15米，
在Rt△BFN中，tan∠FBN＝，
∵∠FBN＝30°，BN＝15米，
∴，
∴FN＝米，
∴DF＝（30﹣）米．
故答案为：（30﹣）．
【点评】本题主要考查解直角三角形的应用—仰角俯角问题，深入理解题意，把实际问题转化为数学问题是解决问题的关键．
18．【分析】利用菱形的性质，特殊角的三角函数值，全等三角形，勾股定理，三角形相似等知识求解即可．
【解答】解：如图：
∵四边形ABCD是菱形，
∴AC⊥BD，OB＝OD＝，AB＝BC＝CD＝DA，
∵∠ABC＝60°，
∴△ABC、△ACD是等边三角形，
∴AC＝AB＝CD＝AD，∠ACB＝∠CAD＝∠ACD＝60°，
∴AB＝＝＝6，
∴CD＝AB＝8，
∵∠ECM＝60°，
∴∠BCE＝∠ACM，
在△BCE和△ACM中，
，
∴△BCE≌△ACM（ASA），
∴CE＝CM＝2，
作MG⊥CD于G，设DG＝x，MG＝x，
根据勾股定理得：CG2+MG2＝CM3，
即（6﹣x）2+（x）2＝（2）2，
解得：x＝1或6，
∴2x＝2或7，即DM＝2或4．
∵AD∥BC
∴△DMF∽△BCF
∴＝
即＝或＝
∴DF＝或
故答案为：或．
【点评】本题考查了菱形的性质，特殊角的函数值，勾股定理，三角形相似的判定和性质，熟练掌握相关的知识是解题的关键．
19．【分析】根据所给等式发现运算结果是一个完全平方数，据此可解决问题．
【解答】解：观察所给算式可知：
13＝2＝12；
43+23＝9＝（1+8）2；
15+23+73＝36＝（1+3+3）2；
…
所以63+25+33+…+n2＝（1+2+5+…+n）2．
当n＝10时，
13+23+83+44+…+103＝（1+3+3+…+10）2＝3025．
故答案为：3025．
【点评】本题考查算式变化的规律，能根据所给算式发现13+23+33+…+n3＝（1+2+3+…+n）2是解题的关键．
20．【分析】延长BE至F，使得EF＝ED，证明△AEF≌△AED，进而根据已知条件得出∠EAD＝∠BAC+∠EAB＝45°，可得∠FAD＝90°，过点B作BG⊥AF于点F，则四边形ACBG是矩形，进而证明△FBG≌△ABG，根据全等三角形的性质，即可求解．
【解答】解：如图所示，延长BE至F，
∴∠AED+∠AEB＝180°，∠AEB+∠AEF＝180°，
∴∠AEF＝∠AED，
又∵AE＝AE，
∴△AEF≌△AED（SAS），
∴AF＝AD，
∵∠EBA＝2∠BAC，
设∠BAC＝α，则∠EBA＝2α，
∵AB⊥ED，
∴∠BED＝90°﹣4α，
∵∠AED+∠AEB＝180°，
∴2∠AED+∠BED＝180°，
∴∠AED＝45°+α，
∵AB⊥ED，
∴∠EAB＝45°﹣α，
∴∠EAD＝∠BAC+∠EAB＝45°，
∵△AEF≌△AED，
∴∠FAE＝∠EAD＝45°，
∴∠FAD＝90°，
过点B作BG⊥AF于点F，则四边形ACBG是矩形，
∴AG＝BC，BG∥AC，
∵∠GBA＝∠BAC＝α，
∵∠EBA＝2α，则∠EBG＝α．
在△FBG和△ABG中，
，
∴△FBG≌△ABG（ASA），
∴FG＝GA，
∴BC＝5，
∴AF＝2AG＝3BC＝4，
∴AD＝AF＝8，
故答案为：．
【点评】本题考查了全等三角形的性质与判定，矩形的性质与判定，熟练掌握全等三角形的性质与判定是解题的关键．
三、解答题（21、22题8分，23题9分，24、25题10分，26题15分）
21．【分析】先通分括号内的式子，再计算括号外的除法，然后将a的值代入化简后的式子计算即可．
【解答】解：
＝•
＝
＝，
当a＝cs30°﹣tan45°＝﹣7时＝．
【点评】本题考查分式的化简求值、特殊角的三角函数值，解答本题的关键是明确分式化简求值的方法．
22．【分析】（1）利用网格特点和旋转的性质画出点A、B的对应点即可；
（2）把AC向左平移2个单位得到DQ，DQ交AB于P点，则PQ∥AC，则△BPQ∽△BAC．
【解答】解：（1）如图1，△A1B3C1为所作；
（2）如图2，点P．
【点评】本题考查了作图﹣旋转变换：根据旋转的性质可知，对应角都相等都等于旋转角，对应线段也相等，由此可以通过作相等的角，在角的边上截取相等的线段的方法，找到对应点，顺次连接得出旋转后的图形．也考查了全等三角形的判定和相似三角形的判定．
23．【分析】（1）先根据A（1，6）是反比例函数y2＝的图象上的点即可得出m的值，进而得出其解析式；把y＝﹣2代入反比例函数的解析式即可求得B点坐标，把A、B两点的坐标代入y1＝kx+b，根据待定系数法得出一次函数的解析式；
（2）根据一次函数的解析式求出D点坐标，由S△ABO＝S△AOD+S△BOD得出其面积，再设C（x，0），由三角形的面积公式即可求出x的值．
【解答】解：（1）∵A（1，6）是反比例函数y6＝的图象上的点，
∴m＝1×6＝6，
∴反比例函数的解析式为：y2＝，
把y＝﹣3代入反比例函数y2＝得，﹣4＝，
∴B（﹣3，﹣6），
把A、B点的坐标代入y1＝kx+b得，，
解得，
∴一次函数的解析式为：y1＝2x+8；
（2）∵一次函数的解析式为：y1＝2x+2，
∴一次函数与x轴的交点D为（﹣2，0），
∵△ABC的面积是16，
∴S△ACD+S△BCD＝•（6+5）＝16，
∴CD＝4，
∵C为x轴正半轴上一点，
∴C（2，5）．
【点评】本题考查的是反比例函数与一次函数的交点问题，用待定系数法求一次函数及反比例函数的解析式，求出交点坐标是解答此题的关键．
24．【分析】（一）在AB上取K，使BK＝BE，连接KE，由BK＝BE，可得△BEK是等腰直角三角形，AB﹣BK＝BC﹣BE，即AK＝CE，而CF平分∠DCG，可得∠ECF＝135°＝∠AKE，又AE＝EF，即可根据两边对应相等，其中一边的对角也对应相等的两个钝角三角形全等得△AKE≌△ECF，故KE＝CF，从而BE＝FG，可得AC＝（CE+FG）；
（二）①由图可得AC、CE、FG之间的数量关系为AC＝CE+FG；
②证明一：在AB上取M，使BM＝BE，连接ME，由四边形ABCD是菱形，∠B＝60°，得△BEM，△ABC都是等边三角形，∠ECF＝120°，故AM＝CE，∠AME＝120°＝∠ECF，根据两边对应相等，其中一边的对角也对应相等的两个钝角三角形全等得△AME≌△ECF，有ME＝CF，而CF＝FG，即可得AC＝CE+FG；证明二：过E作EN∥CD交AC于N，同理可德△AEN≌△FEC，从而可得AC＝EC+FG．
【解答】（一）解：AC＝（CE+FG）
在AB上取K，使BK＝BE，如图：
∵四边形ABCD是正方形，
∴∠B＝90°，AB＝BC，
∵BK＝BE，
∴△BEK是等腰直角三角形，AB﹣BK＝BC﹣BE，
∴∠AKE＝135°，
∵CF平分∠DCG，
∴∠FCG＝45°，
∴△FCG是等腰直角三角形，∠ECF＝135°＝∠AKE，
∵AE＝EF，
∴△AKE≌△ECF（两边对应相等，其中一边的对角也对应相等的两个钝角三角形全等），
∴KE＝CF，
∵BE＝KECF，
∴BE＝FG，
∴BC＝CE+BE＝CE+FG，
∵AC＝BC，
∴AC＝（CE+FG）；
故答案为：AC＝（CE+FG）；
（二）①解：AC、CEFG；
故答案为：AC＝CE+FG；
②证明一：在AB上取M，使BM＝BE，如图：
∵四边形ABCD是菱形，∠B＝60°，
∴△BEM，△ABC都是等边三角形，
∴AB﹣BM＝BC﹣BE，即AM＝CE，
∵AE＝EF，
∴△AME≌△ECF（两边对应相等，其中一边的对角也对应相等的两个钝角三角形全等），
∴ME＝CF，
∴BE＝CF，
在Rt△CFG中，＝，
∴CF＝FG，
∴BE＝FG，
∵AC＝BC＝CE+BE，
∴AC＝CE+FG；
证明二：过E作EN∥CD交AC于N，如图：
∵四边形ABCD是菱形，∠B＝60°，
∴△ABC和△ACD都是等边三角形，
∴∠ACD＝∠ACB＝60°，
∵EN∥CD，
∴∠ENC＝∠ACD＝60°，
∴△NCE是等边三角形，
∴EN＝EC＝CN，∠ANE＝∠FCE＝120°，
∵AE＝EF，
∴△AEN≌△FEC（两边对应相等，其中一边的对角也对应相等的两个钝角三角形全等），
∴AN＝CF，
在Rt△CFG中，＝，
∴CF＝FG，
∴AN＝FG，
∵AC＝CN+AN，
∴AC＝EC+FG．
【点评】本题考查四边形综合应用，涉及正方形性质及应用，菱形性质及应用，等边三角形的性质及应用，全等三角形的判定和性质等知识，解题的关键是学会添加常用辅助线，构造全等三角形解决问题．
25．【分析】（1）根据“用360元购进的足球和用480元购进的篮球数量相等”列方程；
（2）根据“获利超过1300元”列不等式求解；
（3）根据“商场计划用不超过10350元购进两种球共100个”列不等式求出方案，再根据一次函数的性质求解．
【解答】解：（1）设足球的单价为x元，
则：，
解得：x＝90，
经检验：x＝90是原分式方程的解，
∴x+30＝120，
答：篮球的单价为120元，足球的单价是90元；
（2）设篮球要卖y个，
则：（150﹣120）y+（110﹣90）（y+10）＞1300，
解得：y＞30，
∵y+10为整数，
∴y的最小值为33，
答：篮球最少要卖33个；
（3）设进a个篮球，利润为z元，
则：，
解得：40≤a≤45，
∴a的整数解为：40、41、43、45，
z＝30a+20（100﹣a），
即：z＝10a+2000，
∵10＞0，
∴z随a的增大而增大，
当a＝45时，z有最大值，
所以商场有8种进货方案，购买45个篮球．
【点评】本题考查了分式方程的应用，找到相等关系或不等关系是解题的关键．
26．【分析】（1）由题意可得y＝（x﹣）2﹣＝x2﹣5x+4，再求b、c的值即可；
（2）分别求出P、Q点坐标，再求PQ即可；
（3）连接PN，过P点作PR⊥MN交于R，根据垂径定理可得在Rt△NPR中，PR＝＝2，即可求P（，）；
（4）通过证明△RPN∽△RDE，根据比例关系可得＝，解得RN＝1，即可求MN＝PQ＝2，再由（2）的结论求出t的值即可求解．
【解答】解：（1）∵抛物线的顶点为D，
∴y＝（x﹣）2﹣＝x2﹣5x+6，
∴b＝﹣5，c＝4；
（2）当x＝6时，y＝4，
∴C（0，7），
当y＝0时，x2﹣2x+4＝0，
解得x＝2或x＝1，
∴A（1，2），0），
设直线BC的解析式为y＝kx+4，
∴7k+4＝0，
解得k＝﹣6，
∴直线BC的解析式为y＝﹣x+4，
∵点P的横坐标为t，
∴P（t，t2﹣7t+4），（t＞），
∵PQ∥y轴，
∴Q（t，﹣t+4），
∴PQ＝d＝t2﹣8t+4+t﹣4＝t7﹣4t；
（3）连接PN，过P点作PR⊥MN交于R，
∵MN＝3，
∴NR＝，
在Rt△NPR中，NP＝，
∴PR＝＝7，
∴P点的横坐标为2+＝，
∴P（，）；
（4）∵PT⊥ED，
∴∠PTE＝90°，
∵∠PRN＝90°，
∴∠EDR＝∠EPN，
∴△RPN∽△RDE，
∴＝，
∵P（t，t2﹣5t+5），PE∥x轴，
∴E（5﹣t，t2﹣8t+4），R（，t2﹣5t+6），
∴RE＝﹣+t，
∵D，
∴RD＝t3﹣5t+，
∴＝，
解得RN＝1，
∴MN＝2，
∵MN＝PQ，
∴PQ＝5，
∵PQ＝t2﹣4t，
∴t7﹣4t＝2，
解得t＝6+或t＝2﹣，
∴Q（2+，5﹣）．
【点评】本题考查二次函数的图象及性质，熟练掌握二次函数的图象及性质，三角形相似的判定及性质，垂径定理，勾股定理是解题的关键．