北京市第十四中学2024-2025学年九年级上学期期中考试数学试卷

这是一份北京市第十四中学2024-2025学年九年级上学期期中考试数学试卷，共11页。试卷主要包含了11， 证明等内容，欢迎下载使用。

2024.11
班级：________________________ 姓名：_______________
一、选择题（本题共16分，每小题2分）
1．下列图形中，既是轴对称图形又是中心对称图形的为（ ）
A. B. C. D.
2．抛物线 y=-2x-32+5的顶点坐标是（ ）
A. 3，5B. -3，5C. 3，-5 D. -3，-5
3．如图，在Rt△ABC中，，，
将△ABC绕点C顺时针旋转α角至，
使得点A’恰好落在AB边上，则α等于（ ）
A. 150° B. 90° C. 30° D. 60°
4．若关于x的一元二次方程kx2-2x-1=0有两个实数根，则k的取值范围是（ ）
A．k≥1B．k≥-1C．k≥-1且k≠0D．k＞-1且k≠0
5．如图，点A，B，C都在⊙O上，OC⊥OB，点A在BC上，且OA=AB，
则∠ABC的度数是（ ）
A. 15°B. 20° C. 25°D. 30°
6．某厂家2024年1~5月份某种产品的产量统计图如图所示.
设从2月份到4月份，该厂家这种产品产量的月平均增长率
为x，根据题意可得方程（ ）
A. 180(1-x)2=461 B. 368(1+x)2=442
C. 180(1+x)2=461 D. 137(1+x)2=442
7．如图，抛物线y=-116x2+1与x轴交于A，B两点，D是以点C(0,-3)为圆心，2为半径的
圆上的动点，E是线段BD的中点，
连接OE，则线段OE的最大值是（ ）
2 B. 52
C. 3 D. 72
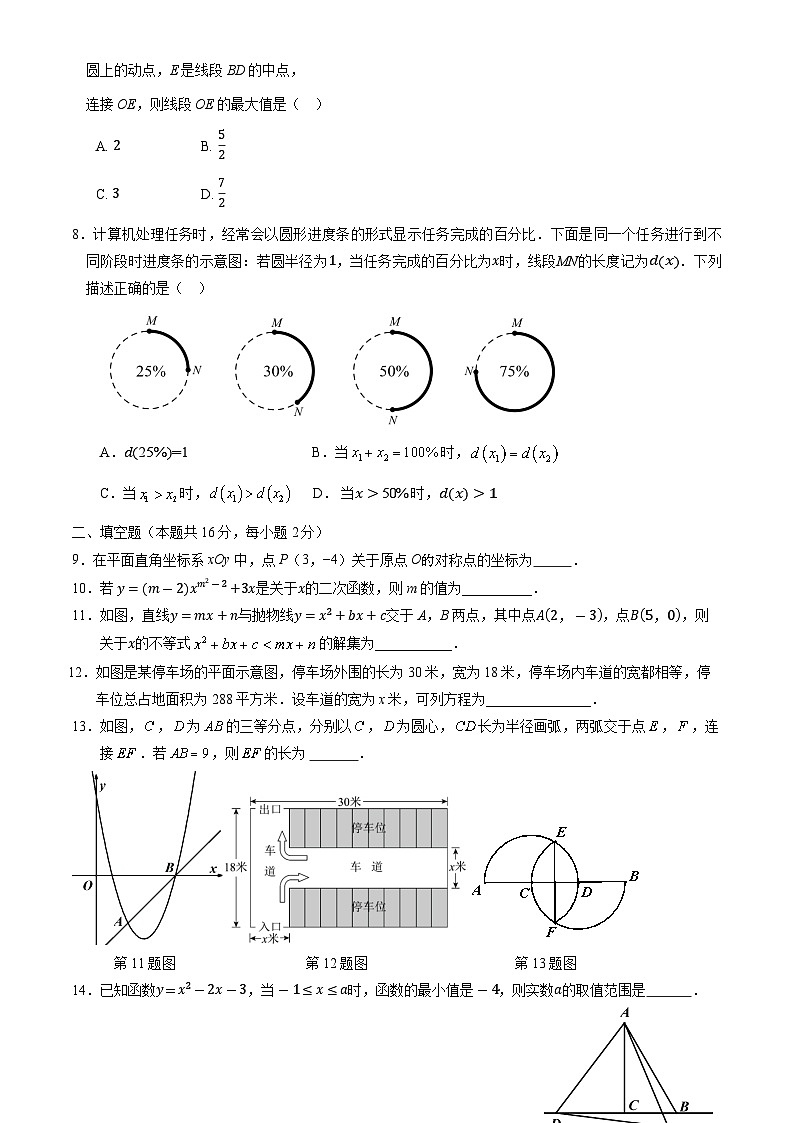
8．计算机处理任务时，经常会以圆形进度条的形式显示任务完成的百分比．下面是同一个任务进行到不同阶段时进度条的示意图：若圆半径为1，当任务完成的百分比为x时，线段MN的长度记为d(x)．下列描述正确的是（ ）
A．d(25%)=1 B．当时，
C．当时， D． 当x>50%时，d(x)>1
二、填空题（本题共16分，每小题2分）
9．在平面直角坐标系xOy中，点P（3，−4）关于原点O的对称点的坐标为 ．
10．若 y=m-2xm2-2+3x是关于x的二次函数，则m的值为__________．
11．如图，直线y=mx+n与抛物线y=x2+bx+c交于A，B两点，其中点A2，-3，点B5，0，则关于x的不等式的解集为___________．
12．如图是某停车场的平面示意图，停车场外围的长为30米，宽为18米，停车场内车道的宽都相等，停车位总占地面积为288平方米．设车道的宽为x米，可列方程为_______________．
13．如图，，为的三等分点，分别以，为圆心，长为半径画弧，两弧交于点，，连接．若，则的长为 ．
第11题图 第12题图 第13题图
14．已知函数y＝x2-2x-3，当-1≤x≤a时，函数的最小值是-4，则实数a的取值范围是 ．
15．在二次函数中， y与x的部分对应值如表：
则m，n的大小关系为m n．（填“>”、“=”或“<”）
如图，已知Rt∆ABC，∠ACB=90°，∠B=60°, AC=43，
点D在CB所在直线上运动，以AD为边作等边三角形ADE，则CB= ___________；
在点D运动过程中，CE的最小值___________．
三、解答题（本题共68分，第17题12分，第18、20、22题，每题5分，第19题4分，
第21、23、24、26、27题，每题6分，第25题7分）
17．解下列方程：
（1）16x2-1=0 （2）x2+4x-9=2x-11
（3）2x2-22x+1=0
18．已知二次函数y=x2-4x+3．
（1）将y＝x2-4x+3化成y＝ax-h2+k的形式：__________________；
（2）抛物线与x轴的交点坐标为 ；
（3）在平面直角坐标系xOy中，画出这个二次函数的图象；
（4）结合图象写出y＞0时，自变量x的取值范围是 ；
（5）当0＜x＜3时，y的取值范围是 ．
图1
19．下面是李雷设计的“过圆上一点作圆的切线”的尺规作图过程．
已知：如图1，⊙O及⊙O上一点P．
求作：过点P的⊙O的切线．
作法：如图2，
①作射线OP；
②在直线OP外任取一点A，以点A为圆心，AP为半径作⊙A，与射线OP交于另一点B；
③连接BA并延长与⊙A交于点C；
图2
④作直线PC；
则直线PC即为所求．
根据李雷设计的尺规作图过程，
（1）使用直尺和圆规，在图2中补全图形；
（保留作图痕迹）
（2）完成下面的证明：
证明：∵BC是⊙A的直径，
∴∠BPC＝90°（ ）（填推理的依据）．
∴OP⊥PC．
∵OP是⊙O的半径，
∴PC是⊙O的切线（ ）（填推理的依据）．
20．已知关于x的一元二次方程.
（1）求证：不论m为何值，该方程总有两个实数根；
（2）若x=2是该方程的根，求代数式m-22-22m-3的值．
21．如图，在平面直角坐标系xOy中，△ABC的三个顶
点分别为A（－3，4），B（－5，1），C（－1，2）．
（1）画出△ABC关于原点对称的△A1B1C1，并写出
点B1的坐标；
（2）画出△ABC绕原点逆时针旋转90°后的△A2B2C2，
并写出点B2的坐标．
22．如图1是博物馆展出的古代车轮实物，《周礼·考工记》记载：“……故兵车之轮六尺有六寸，田车之轮六尺有三寸……”据此，我们可以通过计算车轮的半径来验证车轮类型，请将以下推理过程补充完整．
如图2所示，在车轮上取A、B两点，设AB所在圆的圆心为O，半径为r cm．
作弦AB的垂线OC，D为垂足，则D是AB的中点．其推理的依据是： ．
经测量，AB＝90cm，CD＝15cm，则AD＝ cm；
用含r的代数式表示OD，OD＝ cm．
在Rt△OAD中，由勾股定理可列出关于r的方程： ，
解得r＝ .
通过单位换算，得到车轮直径约为六尺六寸，可验证此车轮为兵车之轮．
23．小明进行铅球训练，他尝试利用数学模型来研究铅球的运动情况．他以水平方向为轴方向，1 m为单位长度，建立了如图所示的平面直角坐标系，铅球从y轴上的A点出手，运动路径可看作抛物线，在B点处达到最高位置，落在x轴上的点C处．小明某次试投时的数据如图所示．
（1）根据图中信息，求出铅球路径所在抛物线的解析式；
（2）若铅球投掷距离（铅球落地点C与出手点A的水平距离OC的长度）不小于10 m，成绩为优秀．请通过计算，判断小明此次试投的成绩是否能达到优秀．
24．如图，四边形ABCD是⊙O的内接四边形，BD为直径，AE是⊙O切线，且AE⊥CD，交CD的延长线于点E．
（1）求证：DA平分∠BDE；
（2）若AE＝4，CD＝6，求⊙O的半径和AD的长．
25．如图，已知点Mx1，y1，Nx2，y2在二次函数y=ax-22-1 a>0的图象上，
且x2-x1=3．
（1）若二次函数的图象经过点3，1．
①求这个二次函数的解析式；
②若y1=y2，求顶点到MN的距离；
（2）当x1≤x≤x2时，二次函数的最大值与最小值的差为1，
点M，N在对称轴的异侧，直接写出a的取值范围．

26．已知：Rt△ABC中，∠ACB＝90°，AC＝BC．
（1）如图1，点D是BC边上一点（不与点B，C重合），连接AD，过点B作BE⊥AD，
交AD的延长线于点E，连接CE．
①若∠BAD＝α，则∠DBE= (用含α的式子表示)；
②用等式表示线段EA，EB和EC之间的数量关系，并证明．
（2）如图2，点D在线段BC的延长线上时，连接AD，过点B作BE⊥AD，垂足E在线段AD上，连接CE．
①依题意补全图2；
②直接写出线段EA，EB和EC之间的数量关系．
图1 图2
27．在平面直角坐标系xOy中的⊙W上，有弦MN，取MN的中点P，将点P绕原点O顺时针
旋转90°得到点Q，称点Q为弦MN的“中点对应点”．设⊙W是以W-3，0为圆心，
半径为2的圆．
（1）已知弦MN长度为2，点Q为弦MN的“中点对应点”．
①如图1,当MN∥x轴时，在图1中画出点Q，并且直接写出线段OQ的长度；
②当MN在圆上运动时，直接写出线段WQ的取值范围．
（2）已知点M-5，0，点N为⊙W上的一动点，设直线y＝x+b与x轴、y轴分别交于
点A、点B，若线段AB上存在弦MN的“中点对应点”点Q，直接写出b的取值范围．
参考答案
一、选择题：（共16分，每小题2分）
二、填空题：（共16分，每小题2分）
9、-3，4 10、 -2 11、 213、 33 14、 a≥1 15、 > 16、 4 ; 23
三、解答题：（共68分，第17题12分，第18、20、22题，每题5分，第19题4分，
第21、23、24、26、27题，每题6分，第25题7分）
17.（1）解：x2=116 ………………………2’
x1=14，x2=-14 ………………………4’
（2）x2+2x+2=0 ………………………1’
∆=22-4×2×1=-4<0 ………………………3’
∴原方程无实根 ………………………4’
（3）∆=-222-4×2×1=0 ………………………2’
x=22±04=22 ………………………3’
∴x1=x2=22 ………………………4’
18. （1）y＝x-22-1； ………………………1’
（2）该图象与x轴的交点坐标为（1，0）或（3，0）； ………………………2’
（3）用“五点法”描点连线得到函数图象如下： ………………………3’
（4）或； ………………………4’
（5）-1≤y＜3 ． ………………………5’
19．解：（1）如图补全图形； ………………………2’
（2）证明：∵BC是⊙A的直径，
∴∠BPC＝90°（直径所对的圆周角是直角）， ……………3’
∴OP⊥PC．
又∵OP是⊙O的半径，
∴PC是⊙O的切线（切线的判定定理）． ………………………4’
20. （1）证明：∵， ………………………1’
∴不论m为何值，该方程总有两个实数根； …………………2’
（2）解：把x=2代入方程得4-8m+m2=0，
即:m2-8m=-4， ………………………3’
∴原式=m2-8m+10 ………………………4’
C1
=-4+10=6． ………………………5’
21.解：（1）如图△A1B1C1为所求，点B1的坐标为（5，−1）；
………………………3’
（2）如图△A2B2C2为所求，点B2的坐标为（−1，−5）．
………………………6’
22.解：如图2所示，在车轮上取A、B两点，设弧AB所在圆的圆心为O，半径为r cm．
作弦AB的垂线OC，D为垂足，则D是AB的中点．
其推理依据是：垂径定理（或“垂直于弦的直径平分弦”）． ………………1’
经测量：AB=90cm，CD=15cm，则AD= 45 cm； ………………………2’
用含r的代数式表示OD，OD=（r-15） cm． ………………………3’
在Rt△OAD中，由勾股定理可列出关于r的方程：
r2=452+r-152 , ………………………4’
解得r=75 ． ………………………5’
23．（1）解：依题意，抛物线的顶点的坐标为，点的坐标为．
设该抛物线的表达式为，……………1’
由抛物线过点，有．
解得， ……………………2’
该抛物线的解析式为； ……………………3’
（2）解：令，得． …………………4’
解得，在轴正半轴，故舍去）． ……………5’
点的坐标为，．
．
由，可得．
小明此次试投的成绩达到优秀． ………………………6’
24．（1）证明：连接OA，
∵AE是⊙O切线，
∴AE⊥半径OA …………………1’
∴∠OAE＝90°，
∵AE⊥CD，
∴OA∥DE，
∴∠OAD＝∠ADE， ………………………2’
∵OA＝OD，
∴∠OAD＝∠ADO，
∴∠ADE＝∠ADO，
∴DA平分∠BDE； …………………3’
（2）解：过点O作OF⊥CD，垂足为F，
∵CD＝6，
∴DF＝FC＝DC＝3，∠OFD＝90°， ………………………4’
∵∠OAE＝∠E＝90°，
∴四边形AEFO是矩形，
∴EF＝OA，AE＝OF＝4， ………………………5’
∴DE＝EF﹣DF＝OA-3，
在Rt△OFD中，根据勾股定理得：OD2＝OF2+DF2，
∴OD2＝42+32，
∴OD＝5，
∴DE＝OA﹣3＝5﹣3＝2，
在Rt△AED中，AD＝AE2+DE2=42+22=25，
∴⊙O的半径为5，AD的长为25． ………………………6’
25.（1）解：①将点代入中，
∴，解得，
∴二次函数的解析式为：； ………………………2’
②当时，此时为平行x轴的直线，
将代入二次函数中得到：，
将代入二次函数中得到：，
∵， ∴=，
整理得到：，
又∵，代入上式得到：，解出，
∴y2=y1=2×122-8×12+7=72，即直线为：，
又∵二次函数的顶点坐标为(2，-1)，
∴顶点(2, −1)到的距离为； ………………………5’
(2) a的取值范围为． ………………………7’
26.解：（1）①∠DBE＝45°-α； ……………1’
②结论：AE-BEEC．
证明：如图，过点C作CR⊥CE交AE于R．
∴∠ACB＝∠RCE＝90°，
∴∠ACR＝∠BCE，
∵∠CAR+∠ADC＝90°，∠CBE+∠BDE＝90°，∠ADC＝∠BDE，
∴∠CAR＝∠CBE， ………………2’
在△ACR和△BCE中，
，
∴△ACR≌△BCE（ASA）， ………………3’
∴AR＝BE，CR＝CE，
∴△CER是等腰直角三角形，
∴ERCE，
∴AE-BE＝AE-AR＝ER EC． ………………………4’
（2）①补全图形，如图2所示： ……………5’
② EB-EAEC． ………………6’
27．解：（1）①OQ＝23；(图形1分，OQ值1分) ………………………2’
② 32-3≤WQ≤32+3； ………………………4’
（2） 3≤b≤4+2 ……………6’
注意事项
1.本试卷共十页，共27道小题，满分100分。考试时间120分钟。
2.在答题卡上指定位置贴好条形码，或填涂考号。
3.试题答案一律填涂或书写在答题卡上，在试卷上作答无效。
4.在答题卡上，选择题用2B铅笔作答，其他试题用黑色字迹签字笔作答。
5.答题不得使用任何涂改工具。
出题人：侯玉梅
审核人：黄炜
x
…
−1
0
1.5
2
3
…
y
…
0
2
m
n
0
…
…
…
…
…
1
2
3
4
5
6
7
8
C
A
D
C
A
C
D
B