人教A版数学(选择性必修一讲义)第07讲拓展一：异面直线所成角(学生版+解析)

这是一份人教A版数学(选择性必修一讲义)第07讲拓展一：异面直线所成角(学生版+解析)，共38页。学案主要包含了知识点归纳，题型精讲等内容，欢迎下载使用。
1、（传统法）核心技巧：平移使相交
具体操作，通过平移一条（或2条），使异面直线转化为相交直线，然后在三角形中利用余弦定理求角
2、（向量法）用向量运算求两条直线所成角
已知，为两异面直线，，与，分别是，上的任意两点，，所成的角为，则
①
②.
二、题型精讲
题型01求异面直线所成角（定值）(传统法）
【典例1】（2023春·河北保定·高一定州市第二中学校考阶段练习）在平行六面体中，底面是菱形，，与底面垂直，，分别在和上，且，，，，则异面直与所成角的余弦值为（ ）

A．B．C．D．
【典例2】（2023春·河北张家口·高一河北省尚义县第一中学校考阶段练习）在正方体中，为棱的中点，则异面直线与夹角的余弦值为（ ）
A．0B．C．D．
【典例3】（2023春·河南开封·高一河南省杞县高中校考阶段练习）正方体中，是的中点，则与所成角的余弦值为______．

【变式1】（2023春·吉林四平·高一校考阶段练习）在三棱柱中，平面，，，则异面直线与所成角的余弦值为（ ）
A．B．C．D．
【变式2】（2023春·河南郑州·高一河南省新郑市第一中学校考阶段练习）如图，是半圆柱底面的直径，是半圆柱的高，是上一点，且，为的中点，则异面直线与所成角的余弦值为________．

题型02求异面直线所成角（定值）(向量法）
【典例1】（2023春·湖北武汉·高二校联考期中）如图，在四棱锥中，底面，底面为正方形，，为的中点，为的中点，则异面直线与所成角的余弦值为（ ）
A．B．C．D．
【典例2】（2023·全国·高三专题练习）如图，在三棱锥中，，，平面平面，则异面直线与所成角的余弦值为（ ）
A．B．C．D．
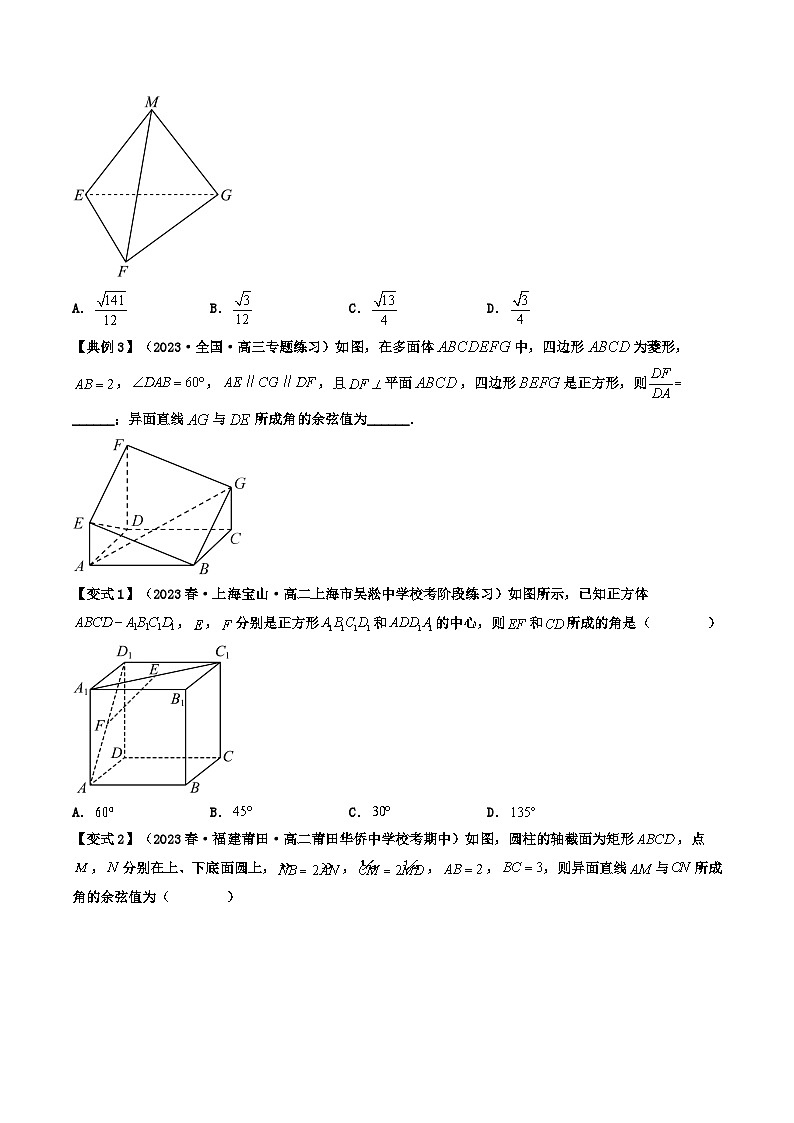
【典例3】（2023·全国·高三专题练习）如图，在多面体中，四边形为菱形，，，，且平面，四边形是正方形，则______；异面直线与所成角的余弦值为______．
【变式1】（2023春·上海宝山·高二上海市吴淞中学校考阶段练习）如图所示，已知正方体，，分别是正方形和的中心，则和所成的角是（ ）
A．B．C．D．
【变式2】（2023春·福建莆田·高二莆田华侨中学校考期中）如图，圆柱的轴截面为矩形，点，分别在上、下底面圆上，，，，，则异面直线与所成角的余弦值为（ ）
A．B．C．D．
【变式3】（2023春·浙江·高一期中）已知直三棱柱的侧棱与底面边长都相等，，分别是和的中点，那么异面直线和所成角的余弦值等于________．
题型03易错题型求异面直线所成角忽略角的取值范围
【典例1】（2023春·江苏·高二校联考阶段练习）如图所示，在棱长为2的正方体中，是棱的中点，=λ，若异面直线和所成角的余弦值为，则异面直线与所成角的余弦值为（ ）

A．B．C．D．
【典例2】（2023春·福建漳州·高二漳州三中校考阶段练习）正方体中，，分别为，的中点，则异面直线与所成角的余弦值为（ ）
A．B．C．D．
【变式1】（2023春·四川成都·高二四川省成都市新都一中校联考期中）如图，将的菱形沿对角线折起，使得平面平面，则异面直线与所成角的余弦值为（ ）
A．B．C．D．
【变式2】（2023秋·浙江宁波·高二统考期末）在四面体中，为正三角形，平面，且，若，，则异面直线和所成角的余弦值等于（ ）
A．B．C．D．
题型04求异面直线所成角（最值或范围）
【典例1】（2023·辽宁大连·校考模拟预测）有很多立体图形都体现了数学的对称美，其中半正多面体是由两种或两种以上的正多边形围成的多面体，半正多面体因其最早由阿基米德研究发现，故也被称作阿基米德体.如图，这是一个棱数为24，棱长为的半正多面体，它的所有顶点都在同一个正方体的表面上，可以看成是由一个正方体截去八个一样的四面体所得.若点为线段上的动点，则直线与直线所成角的余弦值的取值范围为（ ）
A．B．C．D．
【典例2】（2023·全国·高三专题练习）如图，在长方体中，是的中点，点是上一点，2，，动点在上底面上，且满足三棱锥的体积等于1，则直线与所成角的正切值的最小值为_________.
【典例3】（2023·全国·高三专题练习）已知正四面体内接于半径为的球中，在平面内有一动点，且满足，则的最小值是______；直线与直线所成角的取值范围为______.
【变式1】（2023春·江苏南京·高二校考开学考试）如图，四边形中，．现将沿折起，当二面角处于过程中，直线与所成角的余弦值取值范围是（ ）
A．B．C．D．
【变式2】（2023·湖南衡阳·校考模拟预测）如图所示，正方体中，点为底面的中心，点在侧面 的边界及其内部移动，若，则异面直线与所成角的余弦值的最大值为（ ）
A．B．C．D．
【变式3】（2023·全国·高三专题练习）三棱锥中，两两垂直，，点为平面内的动点，且满足，记直线与直线的所成角的余弦值的取值范围为_____________．
题型05已知线线角求参数
【典例1】（2023·全国·高三专题练习）如图，在四棱柱中，底面，且底面为菱形，，，，为的中点，在上，在平面内运动（不与重合），且平面，异面直线与所成角的余弦值为，则的最
大值为___________.
【典例2】（2023·全国·高三专题练习）如图，在四棱锥中，已知平面，且四边形为直角梯形，，，.
（1）求平面与平面所成锐二面角的余弦值；
（2）点是线段上的动点，当直线与所成的角最小时，求线段的长.
【变式2】（2022春·四川绵阳·高二四川省绵阳南山中学校考阶段练习）如图，在四棱锥中，底面，底面是边长为2的正方形，，，分别是，的中点．
(1)求证：平面；
(2)在上是否存在一点，使得与所成角为60°？若存在，求出点的位置，若不存在，请说明理由．

第07讲 拓展一：异面直线所成角（传统法与向量法）
一、知识点归纳
1、（传统法）核心技巧：平移使相交
具体操作，通过平移一条（或2条），使异面直线转化为相交直线，然后在三角形中利用余弦定理求角
2、（向量法）用向量运算求两条直线所成角
已知，为两异面直线，，与，分别是，上的任意两点，，所成的角为，则
①
②.
二、题型精讲
题型01求异面直线所成角（定值）(传统法）
【典例1】（2023春·河北保定·高一定州市第二中学校考阶段练习）在平行六面体中，底面是菱形，，与底面垂直，，分别在和上，且，，，，则异面直与所成角的余弦值为（ ）

A．B．C．D．
【答案】B
【详解】取DM中点K，连接、，

因为，，所以四边形为平行四边形，
所以，所以异面直线与所成角为或其补角.
因为底面是菱形，，，
所以在中，利用余弦定理得，
又，，
在中，利用余弦定理得，
所以异面直与所成角的余弦值为.
故选：B.
【典例2】（2023春·河北张家口·高一河北省尚义县第一中学校考阶段练习）在正方体中，为棱的中点，则异面直线与夹角的余弦值为（ ）
A．0B．C．D．
【答案】D
【详解】取中点，连接，延长至点，使得，连接，
则，所以四边形是平行四边形，所以，
因为,，所以四边形是平行四边形，所以，
所以，
所以是异面直线与夹角或其补角，

设正方体棱长为1，则，
在中，，
在中，，
在中，由余弦定理得，，
所以异面直线与夹角的余弦值为.
故选：D
【典例3】（2023春·河南开封·高一河南省杞县高中校考阶段练习）正方体中，是的中点，则与所成角的余弦值为______．

【答案】/
【详解】在正方体右侧作出一个全等的正方体，连接，如图，

易知，所以四边形是平行四边形，则，
所以是与所成角的平面角或补角，
不妨设正方体的棱长为，
则在正方体中，，
在中，，
在中，，
所以在中，，
所以与所成角的余弦值为.
故答案为：.
【变式1】（2023春·吉林四平·高一校考阶段练习）在三棱柱中，平面，，，则异面直线与所成角的余弦值为（ ）
A．B．C．D．
【答案】D
【详解】在三棱柱中，平面，，
将三棱柱补成长方体，设，则，

因为且，故四边形为平行四边形，所以，且，
故与所成角为或其补角，
在中，，
，，
由余弦定理可得，
因此，直线与所成角的余弦值为.
故选：D.
【变式2】（2023春·河南郑州·高一河南省新郑市第一中学校考阶段练习）如图，是半圆柱底面的直径，是半圆柱的高，是上一点，且，为的中点，则异面直线与所成角的余弦值为________．

【答案】/
【详解】设，
如图，取PC的中点E，连接DE，AE，可得，
所以异面直线AD与BC所成的角为（或其补角）．
又因为平面，平面，则，
且，，平面PAC，
所以平面PAC．
且平面PAC，则，所以．
因为，
所以在中，．
故答案为：.

题型02求异面直线所成角（定值）(向量法）
【典例1】（2023春·湖北武汉·高二校联考期中）如图，在四棱锥中，底面，底面为正方形，，为的中点，为的中点，则异面直线与所成角的余弦值为（ ）
A．B．C．D．
【答案】B
【详解】
如图，以点为坐标原点，建立空间直角坐标系，设，
则，，，，，
则，，
所以，，
所以，
所以，异面直线与所成角的余弦值为.
故选：B.
【典例2】（2023·全国·高三专题练习）如图，在三棱锥中，，，平面平面，则异面直线与所成角的余弦值为（ ）
A．B．C．D．
【答案】D
【详解】解法一
如图，设O，C，D分别为线段，，的中点，连接，，，则，，，，
∴是异面直线与所成的角或其补角.
∵，为的中点，∴，，
∵平面平面，平面平面，∴平面.
设为的中点，连接，，则平面，
， ， ，
∴，连接，易得，，
∴在中，，
∴，
∴，
∴异面直线与所成角的余弦值为.
故选：D.
解法二
如图，设为线段的中点，连接，，
∵，∴，，
∵平面平面，平面平面，∴平面，
∵，∴，，故以为坐标原点，
，，所在直线分别为轴、轴、轴建立空间直角坐标系，
∴，M（0，0，3），， ，∴，，
∴，
∴异面直线与所成角的余弦值为.
故选:D.
【典例3】（2023·全国·高三专题练习）如图，在多面体中，四边形为菱形，，，，且平面，四边形是正方形，则______；异面直线与所成角的余弦值为______．
【答案】 /
【详解】由四边形为菱形，，可得为正三角形，
设为的中点，连接，所以．又，因此．
又平面，故以为原点，以为轴，为轴，为轴，建立空间直角坐标系，
如图
设，，则，，，，
由题意，则平面，平面，
设，，从而，
因为四边形BEFG是正方形，所以，所以，
即，解得，所以，，设，
则，因为，所以，所以，即，所以，所以；
设异面直线AG与DE所成角为，又，
所以，
所以异面直线AG与DE所成角的余弦值为.
故答案为：；
【变式1】（2023春·上海宝山·高二上海市吴淞中学校考阶段练习）如图所示，已知正方体，，分别是正方形和的中心，则和所成的角是（ ）
A．B．C．D．
【答案】B
【详解】如图建立空间直角坐标系，令正方体的棱长为，则，，，，
所以，，
设和所成的角为，则，
因为，所以.
故选：B
【变式2】（2023春·福建莆田·高二莆田华侨中学校考期中）如图，圆柱的轴截面为矩形，点，分别在上、下底面圆上，，，，，则异面直线与所成角的余弦值为（ ）
A．B．C．D．
【答案】D
【详解】方法一 如图（1），在上取点，使，连接，，，，．
易知四边形为矩形，则，且．
连接，．因为，且，
所以四边形为平行四边形，所以，且．
连接，则，且，
所以四边形为平行四边形，则，
所以或其补角是异面直线与所成的角．
在中，，，所以．
在中，，，所以．又，
所以．
故选：D．
方法二 如图（2），在上取点，使，连接，，，．
易知四边形为矩形，，．连接．
由已知条件，得为圆柱的一条母线．
以为坐标原点，分别以直线，，为轴、轴、轴建立如图（2）的空间直角坐标系，
则，，，，
所以，，则，
所以异面直线与所成角的余弦值为．
故选：D．
【变式3】（2023春·浙江·高一期中）已知直三棱柱的侧棱与底面边长都相等，，分别是和的中点，那么异面直线和所成角的余弦值等于________．
【答案】/0.7
【详解】因为直三棱柱的侧棱与底面边长都相等，
所以为等边三角形，取的中点，所以，
因为为的中点，所以，
又因为平面，所以平面，
如图，以为坐标原点，分别以，，所在直线为轴，轴，轴，建立空间直角坐标系，
因为直三棱柱的侧棱与底面边长都相等，设，
则，，，，，，
设异面直线和所成角为，
所以，
即异面直线和所成角的余弦值为.
故答案为：.
题型03易错题型求异面直线所成角忽略角的取值范围
【典例1】（2023春·江苏·高二校联考阶段练习）如图所示，在棱长为2的正方体中，是棱的中点，=λ，若异面直线和所成角的余弦值为，则异面直线与所成角的余弦值为（ ）

A．B．C．D．
【答案】B
【详解】如图，以D为原点，分别以DA，DC，DD1所在直线为x，y，z轴，建立空间直角坐标系，
因为正方体的棱长为2，则A1（2，0，2），D1（0，0，2），E（0，2，1），A（2，0，0）.
所以，
又
所以，整理得到，解得（舍去）,
所以，,
所以，故cs θ=，

故选：B.
【典例2】（2023春·福建漳州·高二漳州三中校考阶段练习）正方体中，，分别为，的中点，则异面直线与所成角的余弦值为（ ）
A．B．C．D．
【答案】D
【详解】如图，建立空间直接坐标系，设正方体的棱长为2，
因为E，F分别为，的中点，易知，A(2，0，0)，E(0，1，2)，
C(0，2，0)，F(2，2，1)，所以，，
所以=.
因为异面直线AE与FC所成角为锐角.
所以异面直线AE与FC所成角的余弦值为.故A，B，C错误.
故选：D.
【变式1】（2023春·四川成都·高二四川省成都市新都一中校联考期中）如图，将的菱形沿对角线折起，使得平面平面，则异面直线与所成角的余弦值为（ ）
A．B．C．D．
【答案】B
【详解】
如图，取BD中点为坐标原点，建立空间直角坐标系，
令，，，，，
则，，
，
，所成角的余弦值为.
故选：.
【变式2】（2023秋·浙江宁波·高二统考期末）在四面体中，为正三角形，平面，且，若，，则异面直线和所成角的余弦值等于（ ）
A．B．C．D．
【答案】A
【详解】因为平面，为正三角形，
故以为原点，以为轴的正方向，建立空间直角坐标系，
设，则，
由，，可得，
所以，
所以，
所以异面直线和所成角的余弦值等于.
故选：A.
题型04求异面直线所成角（最值或范围）
【典例1】（2023·辽宁大连·校考模拟预测）有很多立体图形都体现了数学的对称美，其中半正多面体是由两种或两种以上的正多边形围成的多面体，半正多面体因其最早由阿基米德研究发现，故也被称作阿基米德体.如图，这是一个棱数为24，棱长为的半正多面体，它的所有顶点都在同一个正方体的表面上，可以看成是由一个正方体截去八个一样的四面体所得.若点为线段上的动点，则直线与直线所成角的余弦值的取值范围为（ ）
A．B．C．D．
【答案】C
【详解】将半正多面体补成正方体，建立如图所示的空间直角坐标系.
因为半正多面体的棱长为，故正方体的棱长为
所以，.
设，则.
所以.
令，则，
因为，所以.
故直线与直线所成角的余弦值的取值范围为.
故选：C
【典例2】（2023·全国·高三专题练习）如图，在长方体中，是的中点，点是上一点，2，，动点在上底面上，且满足三棱锥的体积等于1，则直线与所成角的正切值的最小值为_________.
【答案】
【详解】解：以D为坐标原点，分别以所在直线为x轴，y轴，z轴建立空间直角坐标系，
，则，，，
设平面的法向量为
则，令，则，
所以平面的一个法向量
因为
所以点P到平面BFE的距离
因为，
所以在等腰中，到的高为，
所以
因为，
所以
所以或(舍去)，
设直线与所成的角为，则，
所以
，
所以的最大值为，此时最小，此时最小，
因为，且，所以，
所以，即直线CP与所成角的正切值的最小值为，
故答案为：
【典例3】（2023·全国·高三专题练习）已知正四面体内接于半径为的球中，在平面内有一动点，且满足，则的最小值是______；直线与直线所成角的取值范围为______.
【答案】
【详解】在正四面体中，设A在面内的投影为E，故E为三角形的中心，
设正四面体的棱长为x，球O的半径为R，
则 ，
依题意正四面体内接于半径为的球中，故球心O在上，
设球的半径为R,则，
即，解得 ，（舍去），
则，，
又，
故P的轨迹为平面 内以E为圆心，为半径的圆，
而，当三点共线时，且P在之间时，最小，最小值是；
以E为圆心，所在直线为x轴，在底面内过点E作的垂线为y轴，为z轴，建立如图所示直角坐标系，
则,,,，
设，，
故，,
设直线与直线所成角为，
,
因为，故，故，
又，故，故，
故答案为：.
【变式1】（2023春·江苏南京·高二校考开学考试）如图，四边形中，．现将沿折起，当二面角处于过程中，直线与所成角的余弦值取值范围是（ ）
A．B．C．D．
【答案】D
【详解】设向量与所成角为，二面角的平面角大小为，
因为，所以，又，所以，
,，
则，
所以，
取中点E，连接，则，，
,,
在中，，即，
所以，即，
又因为，所以，
因为直线夹角范围为，所以直线与所成角的余弦值范围是．
故选：D．
【变式2】（2023·湖南衡阳·校考模拟预测）如图所示，正方体中，点为底面的中心，点在侧面 的边界及其内部移动，若，则异面直线与所成角的余弦值的最大值为（ ）
A．B．C．D．
【答案】C
【详解】建立如下图所示的空间直角坐标系，设正方体的棱长为2
，，，
设，因为，
所以，则
在侧面内取一点，使得，则
易知三角形为直角三角形，则
设，对称轴为，则
即
故选：C
【变式3】（2023·全国·高三专题练习）三棱锥中，两两垂直，，点为平面内的动点，且满足，记直线与直线的所成角的余弦值的取值范围为_____________．
【答案】
【详解】因为两两垂直，且，所以由勾股定理可知，
所以三棱锥为正三棱锥，记在底面内的投影为，
所以，
因为，所以，所以，
因为，所以，所以的轨迹是以为圆心半径为的圆，
取中点，连接，可知经过点，建立如下图所示的空间直角坐标系：
设，，，
所以，
所以，
设直线与直线的所成角为.
所以
故答案为：.
题型05已知线线角求参数
【典例1】（2023·全国·高三专题练习）如图，在四棱柱中，底面，且底面为菱形，，，，为的中点，在上，在平面内运动（不与重合），且平面，异面直线与所成角的余弦值为，则的最大
值为___________.
【答案】/
【详解】连接交于点，平面，平面，则，
因为四边形为菱形，则，
，、平面，平面，
以点为坐标原点，、、的方向分别为、、轴的正方向建立如下图所示的空间直角坐标系，
则、、、、、、，
易知平面的一个法向量为，
因为平面，所以，，
设点，其中，则，
由已知可得，
因为，解得，即点，
设点，则，
因为，则，可得，且，可得，
所以，点，
因为平面，、平面，，，
且，
所以，.
故答案为：.
【典例2】（2023·全国·高三专题练习）如图，在四棱锥中，已知平面，且四边形为直角梯形，，，.
（1）求平面与平面所成锐二面角的余弦值；
（2）点是线段上的动点，当直线与所成的角最小时，求线段的长.
【答案】(1) (2)
【详解】试题分析：以为正交基底建立如图所示的空间直角坐标系，则各点的坐标为．
（1） 因为平面，所以是平面的一个法向量，．
因为．
设平面的法向量为，则，
即，令，解得．
所以是平面的一个法向量，从而，
所以平面与平面所成二面角的余弦值为．
（2） 因为，设，
又，则，
又，
从而，
设，
则，
当且仅当，即时，的最大值为．
因为在上是减函数，此时直线与所成角取得最小值．
又因为，所以．
【典例3】（2022·天津·校联考一模）如图，在四棱锥中，平面，，，，，为的中点，在上，且.
(1)求证：平面；
(2)求平面与平面夹角的余弦值；
(3)点是线段上异于两端点的任意一点，若满足异面直线与所成角为，求的长.
【答案】(1)证明见解析
(2)
(3)
【详解】（1）证明：因为平面，，，
以点为坐标原点，、、所在直线分别为、、轴建立如下图所示的空间直角坐标系，
则、、、、、、，
，，，，
又平面，平面，平面.
（2）解：设平面的法向量为，，，
则，取，可得，
易知平面的一个法向量为，
所以，，
因此，平面与平面夹角的余弦值为.
（3）解：设，其中，
，，
由题意可得，
整理可得，，解得，
所以，点为线段的中点，则点，所以，.
因此，若异面直线与所成角为，则.
【变式1】（2022秋·辽宁大连·高二育明高中校考期中）已知四棱锥的底面是边长为2的正方形，是以为斜边的等腰直角三角形，平面，是线段上的动点（不含端点），若线段上存在点（不含端点），使得异面直线和所成的角的大小为30°，则线段长的取值范围是______.
【答案】
【详解】设是的中点，则，
由于平面，平面，所以，
由于平面，所以平面，
由于平面，所以平面平面，
以为原点建立如图所示空间直角坐标系，
，，
设；设，
则，
设与所成角为，则，
，
整理得，
函数的开口向下，对称轴为，
所以函数在上递增，
则，，，，，，
∴，，，
设平面PCB的法向量为，
则，即，令，则，，∴，
∴，故平面PCB．
（2）设，则，∴，
∵DM与PC所成角为60°，，
∴，解得，
故在AP上存在一点M，点M为AP中点，使得DM与PC所成角为60°．