人教A版数学(选择性必修一讲义)第35讲拓展四：圆锥曲线的方程(面积问题)(学生版+解析)

这是一份人教A版数学(选择性必修一讲义)第35讲拓展四：圆锥曲线的方程(面积问题)(学生版+解析)，共56页。学案主要包含了知识点归纳，题型精讲等内容，欢迎下载使用。
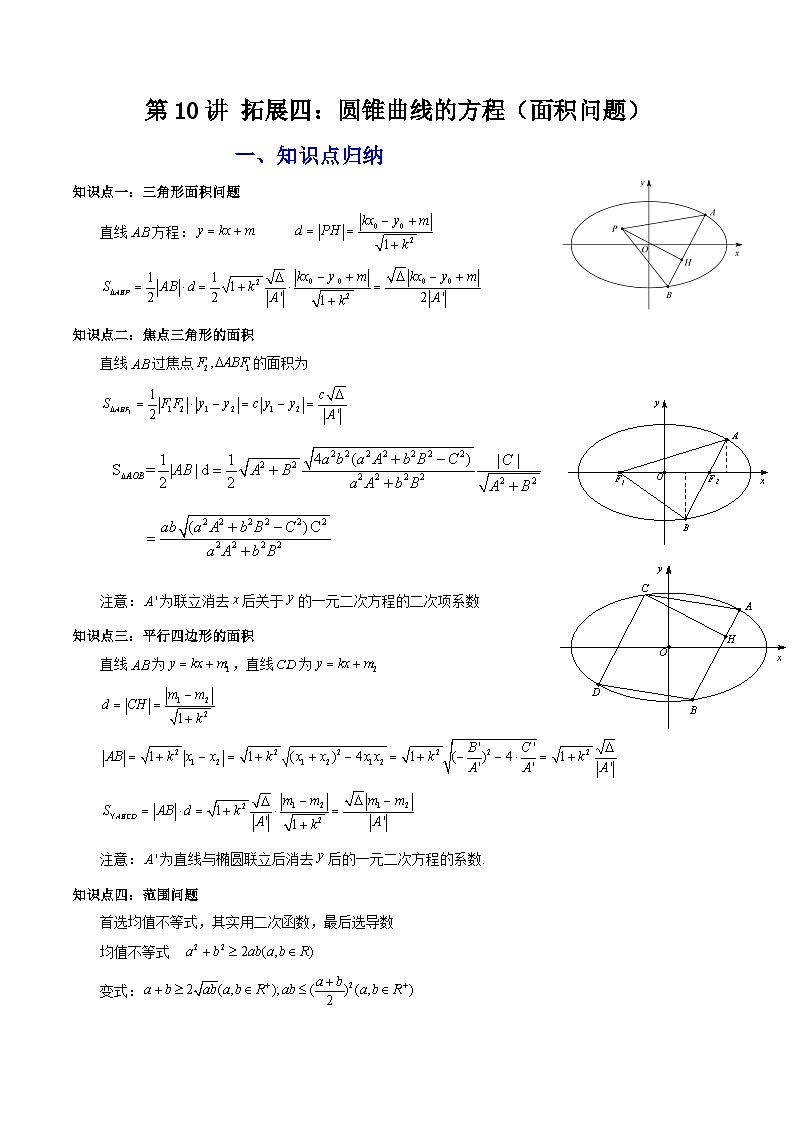
知识点一：三角形面积问题
直线方程：
知识点二：焦点三角形的面积
直线过焦点的面积为

注意：为联立消去后关于的一元二次方程的二次项系数
知识点三：平行四边形的面积
直线为，直线为
注意：为直线与椭圆联立后消去后的一元二次方程的系数.
知识点四：范围问题
首选均值不等式，其实用二次函数，最后选导数
均值不等式
变式：
作用：当两个正数的积为定值时求出这两个正数的和的最小值；
当两个正数的和为定值时求出这两个正数的积的最大值
注意：应用均值不等式求解最值时，应注意“一正二定三相等”
圆锥曲线经常用到的均值不等式形式列举：
（1）（注意分三种情况讨论）
（2）
当且仅当时，等号成立
（3）
当且仅当时等号成立.
（4）
当且仅当时，等号成立
(5)
当且仅当时等号成立.
二、题型精讲
题型01椭圆中三角形（四边形）的面积问题（定值）
【典例1】（2023春·广东广州·高二统考期末）已知椭圆的焦点坐标为、，点为椭圆上一点.
(1)求椭圆的标准方程；
(2)经过点且倾斜角为的直线与椭圆相交于、两点，为坐标原点，求的面积.
【典例2】（2023春·河南南阳·高二校联考阶段练习）已知椭圆C：的一个焦点为，且离心率为．
(1)求椭圆C的方程；
(2)若过椭圆C的左焦点，倾斜角为的直线与椭圆交于A，B两点，O为坐标原点，求的面积．
【典例3】（2023春·湖北·高二黄石二中校联考阶段练习）已知圆，圆，动圆与圆相外切，与圆相内切.
(1)求动圆的圆心的轨迹方程；
(2)过点的两直线，分别交动圆圆心的轨迹于、和、，.求四边形的面积.
【变式1】（2023·湖南长沙·长郡中学校考二模）已知圆是圆上任意一点，线段的垂直平分线与半径相交于点，当点运动时，点的轨迹为曲线．
(1)求曲线的方程；
(2)过点的直线与曲线相交于点，与轴相交于点，过点的另一条直线与相交于两点，且的面积是面积的倍，求直线的方程．

【变式2】（2023·上海闵行·上海市七宝中学校考三模）已知是椭圆的左顶点，是椭圆上不同的两点．
(1)求椭圆的焦距和离心率；
(2)设，若，且、、和、、分别共线，求证：三点共线；
(3)若是椭圆上的点，且，求的面积．
【变式3】（2023春·湖北荆州·高二统考阶段练习）已知椭圆C：的上顶点为K，左右顶点分别为A，B，，的周长为．
(1)求椭圆C的方程；
(2)O为坐标原点，O，B关于直线L对称，过直线L与x轴的交点作斜率为k的直线l与椭圆C交于不同的两点M，N（异于A，B两点），直线AM，AN分别交直线L于P，Q两点，当四边形APBQ的面积为4时，求k的值．
题型02椭圆中三角形（四边形）的面积问题（最值或范围）
【典例1】（2023春·贵州·高二贵州师大附中校联考阶段练习）已知为坐标原点，椭圆的离心率为，的上顶点到右顶点的距离为.
(1)求的方程；
(2)，为上的动点，设直线，的斜率分别为，，且.求的面积的最大值.
【典例2】（2023春·江西赣州·高二校联考阶段练习）已知的两顶点坐标．
(1)求动点的轨迹的方程；
(2)不垂直于轴的动直线与轨迹相交于两点，定点，若直线关于轴对称，求面积的取值范围．
【典例3】（2023春·四川德阳·高二德阳五中校考阶段练习）已知点，动点满足直线与的斜率之积为.记动点的轨迹为曲线.
(1)求曲线的方程，并说明是什么曲线；
(2)设为曲线上的两动点，直线的斜率为，直线的斜率为，且.
①求证：直线恒过一定点；
②设的面积为，求的最大值.
【变式1】（2023·河南·洛宁县第一高级中学校联考模拟预测）已知椭圆：的左、右焦点分别为，，过的直线与交于，两点，的周长为8，且点在上．
(1)求椭圆的方程；
(2)设直线与圆：交于C，D两点，当时，求面积的取值范围．

【变式2】（2023春·上海黄浦·高三上海市大同中学校考阶段练习）已知椭圆．
(1)求该椭圆的离心率；
(2)设点是椭圆C上一点，求证：过点P的椭圆C的切线方程为；
(3)若点M为直线l：x=4上的动点，过点M作该椭圆的切线MA，MB，切点分别为，求△的面积的最小值．
【变式3】（2023·北京大兴·校考三模）已知椭圆过点，且离心率为.
(1)求椭圆的方程；
(2)直线分别交椭圆于、两点，若线段的中点在直线上，求面积的最大值.
题型03双曲线中三角形（四边形）的面积问题（定值）
【典例1】（2023春·上海宝山·高二上海交大附中校考期中）已知双曲线，及直线.
(1)若与有且只有一个公共点，求实数的值；
(2)若与的左右两支分别交于A、B两点，且的面积为，求实数的值.
【典例2】（2023·全国·高三专题练习）已知双曲线C：的一条渐近线方程为，焦点到渐近线的距离为1．
(1)求双曲线C的标准方程与离心率；
(2)已知斜率为的直线与双曲线C交于x轴下方的A，B两点，O为坐标原点，直线OA，OB的斜率之积为，求的面积．
【典例3】（2023·全国·模拟预测）已知双曲线的离心率为，左、右焦点分别为，，焦距为．点在第一象限的双曲线上，过点作双曲线切线与直线交于点．
(1)证明：；
(2)已知斜率为的直线与双曲线左支交于 两点，若直线，的斜率互为相反数，求的面积．
【变式1】（2023·全国·高三专题练习）已知M是平面直角坐标系内的一个动点，直线与直线垂直，A为垂足且位于第一象限，直线与直线垂直，B为垂足且位于第四象限，四边形（O为原点）的面积为8，动点M的轨迹为C.
(1)求轨迹C的方程；
(2)已知是轨迹C上一点，直线l交轨迹C于P，Q两点，直线，的斜率之和为1，，求的面积.
【变式2】（2023春·湖北荆州·高二统考阶段练习）已知双曲线C：的左，右焦点分别为，，且，都在圆上，连接双曲线C的两个实轴端点、两个虚轴端点组成的菱形的面积为．
(1)求双曲线C的标准方程；
(2)设P是双曲线C与圆在第一象限的交点，求的面积．
题型04双曲线中三角形（四边形）的面积问题（最值或范围）
【典例1】（2023春·福建莆田·高二莆田一中校考期中）在平面直角坐标系中，动点到的距离与它到直线的距离之比为2，记的轨迹为曲线.
(1)求曲线的方程；
(2)过的直线交曲线于两点（均位于轴右侧），关于原点的对称点为，求的面积的取值范围.
【典例2】（2023·浙江金华·模拟预测）P是双曲线右支上一点，A，B是双曲线的左右顶点，过A，B分别作直线PA，PB的垂线AQ，BQ，AQ与BQ的交点为Q，PA与BQ的交点为C．
(1)记P，Q的纵坐标分别为，求的值；
(2)记的面积分别为，当时，求的取值范围．
【变式1】（2023·云南昆明·高三昆明一中校考阶段练习）在平面直角坐标系中，点，点.以G为圆心作一个半径为6的圆，点P是圆上一动点，线段AP的垂直平分线与直线GP相交于点Q.
(1)求Q的轨迹方程；
(2)过原点斜率为的直线l交曲线Q于B，C两点，求四边形GBAC面积的最大值.
【变式2】（2023·高二课时练习）如图，已知双曲线，经过点且斜率为的直线与交于两点，与的渐近线交于两点（从左至右的顺序依次为），其中.
(1)若点是的中点，求的值；
(2)求面积的最小值.
【变式3】（2023春·浙江杭州·高三浙江省杭州第二中学校考阶段练习）已知双曲线，
(1)求的值；
(2)若线段的垂直平分线与抛物线交于两点，求的面积.
【变式1】（2023·陕西安康·统考三模）已知抛物线的焦点为.
(1)求抛物线的方程；
(2)过点的直线与抛物线交于两点，为抛物线上的点，且，，求的面积.
【变式2】（2023秋·青海西宁·高二校考期末）设椭圆的四个顶点围成的菱形的面积为4，且点为椭圆上一点.拋物线的焦点与点关于直线对称.
(1)求椭圆及抛物线的方程；
(2)直线与椭圆交于，与拋物线交于（异于原点），若，求四边形的面积.
题型06抛物线中三角形（四边形）的面积问题（最值或范围）
【典例1】（2023·全国·高二专题练习）已知抛物线的顶点为坐标原点，焦点在坐标轴上，设是抛物线上一点．
(1)求抛物线方程；
(2)若抛物线的焦点在x轴上，过点M做两条直线分别交抛物线于A，B两点，若直线与的倾斜角互补，求面积的最大值．
【典例2】（2023秋·高二单元测试）已知抛物线，点在抛物线上，且点到抛物线的焦点的距离为.
(1)求；
(2)设圆，点是圆上的动点，过点作圆的两条切线，分别交抛物线于两点，求的面积的最大值.
【变式1】（2023春·江苏南通·高二期末）抛物线的焦点，过C的焦点F斜率为1的直线交抛物线于A，B两点，的面积为
(1)求抛物线C的方程；
(2)若P为C上位于第一象限的任一点，直线l与C相切于点P，连接PF并延长交C于点M，过P点作l的垂线交C于另一点N，求面积S的最小值．
【变式2】（2023春·四川广安·高二四川省广安友谊中学校考阶段练习）已知抛物线C：的焦点为，且点与圆上点的距离的最小值为．
(1)求的值；
(2)若点在圆上，过点做抛物线的两切线，其中是切点，求面积的最大值．

第10讲 拓展四：圆锥曲线的方程（面积问题）
一、知识点归纳
知识点一：三角形面积问题
直线方程：
知识点二：焦点三角形的面积
直线过焦点的面积为

注意：为联立消去后关于的一元二次方程的二次项系数
知识点三：平行四边形的面积
直线为，直线为
注意：为直线与椭圆联立后消去后的一元二次方程的系数.
知识点四：范围问题
首选均值不等式，其实用二次函数，最后选导数
均值不等式
变式：
作用：当两个正数的积为定值时求出这两个正数的和的最小值；
当两个正数的和为定值时求出这两个正数的积的最大值
注意：应用均值不等式求解最值时，应注意“一正二定三相等”
圆锥曲线经常用到的均值不等式形式列举：
（1）（注意分三种情况讨论）
（2）
当且仅当时，等号成立
（3）
当且仅当时等号成立.
（4）
当且仅当时，等号成立
(5)
当且仅当时等号成立.
二、题型精讲
题型01椭圆中三角形（四边形）的面积问题（定值）
【典例1】（2023春·广东广州·高二统考期末）已知椭圆的焦点坐标为、，点为椭圆上一点.
(1)求椭圆的标准方程；
(2)经过点且倾斜角为的直线与椭圆相交于、两点，为坐标原点，求的面积.
【答案】(1)
(2)
【详解】（1）解：由椭圆的定义可得，
所以，，又因为，则，
所以，椭圆的标准方程为.
（2）解：设点、，由题意可知，直线的方程为，即.
联立可得，解得，，

所以，.
【典例2】（2023春·河南南阳·高二校联考阶段练习）已知椭圆C：的一个焦点为，且离心率为．
(1)求椭圆C的方程；
(2)若过椭圆C的左焦点，倾斜角为的直线与椭圆交于A，B两点，O为坐标原点，求的面积．
【答案】(1)
(2)
【详解】（1）依题意得，，所以，，
所以椭圆C的方程为.
（2）因为直线的倾斜角为，所以斜率为，
又直线过点，所以直线，
联立，消去并整理得，
，
设，，
则，，
所以，
所以.

【典例3】（2023春·湖北·高二黄石二中校联考阶段练习）已知圆，圆，动圆与圆相外切，与圆相内切.
(1)求动圆的圆心的轨迹方程；
(2)过点的两直线，分别交动圆圆心的轨迹于、和、，.求四边形的面积.
【答案】(1)；
(2).
【详解】（1）设动圆的半径为，，∴，，∴，
∴是以，为焦点，以为长轴长的椭圆，
可设方程为，则，，
∴的轨迹方程是；
（2）
设，（为0时不符合题意），，，
联立与椭圆的方程得：，
，
∴ ，
同理设，不为0，可得，
∴，
∴，不妨取， ，
此时，∴
而
，
同理，
∴.
【变式1】（2023·湖南长沙·长郡中学校考二模）已知圆是圆上任意一点，线段的垂直平分线与半径相交于点，当点运动时，点的轨迹为曲线．
(1)求曲线的方程；
(2)过点的直线与曲线相交于点，与轴相交于点，过点的另一条直线与相交于两点，且的面积是面积的倍，求直线的方程．
【答案】(1)
(2)
【详解】（1）因为点为线段的垂直平分线与半径的交点，
所以，所以，
所以点的轨迹是以为焦点，长轴长为4的椭圆，在椭圆中，
所以曲线的方程为．
（2）由已知得，所以直线的方程为，所以点的坐标为．
当直线的斜率不存在时，，或都与已知不符；
当直线的斜率存在时，设直线的方程为，
由得，
易知，则，
，
由的面积是面积的倍可得，
化简得，即，
又，所以，即，也就是，
所以，
解得，
所以直线的方程为．

【变式2】（2023·上海闵行·上海市七宝中学校考三模）已知是椭圆的左顶点，是椭圆上不同的两点．
(1)求椭圆的焦距和离心率；
(2)设，若，且、、和、、分别共线，求证：三点共线；
(3)若是椭圆上的点，且，求的面积．
【答案】(1)焦距为，离心率为
(2)证明见解析
(3)
【详解】（1）由可知，
，，故，
所以焦距，离心率．
（2）设，，
由题意，，，，，，，，
又，
所以，得，
方法一：由三点共线，则，即，
同理可得，三点共线，则，即，
故，即，
又，，
所以，
所以，
由，整理得，
所以有，
又，
故，
所以，
所以三点共线．
方法二：因为，，则，
由得直线的方程为，
与椭圆联立，得，
则，
所以，
同理得，
所以，，即三点共线．

（3）设，
因为，，，
①当直线的斜率不存在时，则，
所以，，
又是椭圆上的点，此时，
故，
②当直线的斜率存在时，可设，
由，得，
所以，，
所以，
又点在椭圆上，代入整理得，，
从而，
于是，
点到直线的距离，
所以．

【变式3】（2023春·湖北荆州·高二统考阶段练习）已知椭圆C：的上顶点为K，左右顶点分别为A，B，，的周长为．
(1)求椭圆C的方程；
(2)O为坐标原点，O，B关于直线L对称，过直线L与x轴的交点作斜率为k的直线l与椭圆C交于不同的两点M，N（异于A，B两点），直线AM，AN分别交直线L于P，Q两点，当四边形APBQ的面积为4时，求k的值．
【答案】(1)
(2)
【详解】（1）∵，∴，①
∵的周长为，
∴，②
联立①②，解得，，
∴椭圆C的方程．
（2）易知，，直线L：，直线L与x轴的交点为，
设直线MN的方程为，
联立直线MN与椭圆的方程，消去y得，
设，，则，，，
直线AM的方程为，令，则，∴；
直线AN的方程为，令，则，∴，
∵四边形APBQ的面积为4，
∴，即，则，
因此，即，
化简得，
将，代入得，
进而，
∴，化简得，
进而，
故．
题型02椭圆中三角形（四边形）的面积问题（最值或范围）
【典例1】（2023春·贵州·高二贵州师大附中校联考阶段练习）已知为坐标原点，椭圆的离心率为，的上顶点到右顶点的距离为.
(1)求的方程；
(2)，为上的动点，设直线，的斜率分别为，，且.求的面积的最大值.
【答案】(1)
(2)1
【详解】（1）由题意，
在椭圆中，离心率为，
由题知：，解得：，
∴椭圆的方程为.
（2）由题意及（1）得，在中，，为上的动点，
设，，所以，，，
∴，即，
由对称性知直线斜率存在，设直线，

将代入，得：，
∴，，，
∵，
∴，
设到直线的距离为，，
∵，
，
当且仅当时取等号，即，时，取最大值1.
【典例2】（2023春·江西赣州·高二校联考阶段练习）已知的两顶点坐标．
(1)求动点的轨迹的方程；
(2)不垂直于轴的动直线与轨迹相交于两点，定点，若直线关于轴对称，求面积的取值范围．
【答案】(1)
(2)
【详解】（1）由，所以，
因此动点的轨迹是以为焦点的椭圆，且去掉椭圆与轴的交点，

设椭圆的标准方程为，则，
解得，
所以动点的轨迹的方程为．
（2）由题意可知直线的斜率不为0，设直线的方程为， 点，
把代入椭圆方程可得：，
，化为．
，
直线关于轴对称，，
即，且，
则，
即，
所以，
化简得，所以，故直线经过定点．
令，
由于在上单调递增，所以，故
因此，．
【典例3】（2023春·四川德阳·高二德阳五中校考阶段练习）已知点，动点满足直线与的斜率之积为.记动点的轨迹为曲线.
(1)求曲线的方程，并说明是什么曲线；
(2)设为曲线上的两动点，直线的斜率为，直线的斜率为，且.
①求证：直线恒过一定点；
②设的面积为，求的最大值.
【答案】(1)，曲线为中心在坐标原点，焦点在轴上的椭圆，不含左､右顶点.
(2)①证明见解析；②最大值为.
【详解】（1）由题意，得，
化简得，
所以曲线为中心在坐标原点，焦点在轴上的椭圆，不含左､右顶点.
（2）如图，

①证明：设.
因为若直线的斜率为0，则点关于轴对称，必有，不合题意，
所以直线的斜率必不为0.
设直线的方程为.
由得，
所以，且
因为点是曲线上一点，
所以由题意可知，
所以，即
因为
所以，此时，
故直线恒过轴上一定点.
②由①可得，，
所以
当且仅当即时等号成立，
所以的最大值为.
【变式1】（2023·河南·洛宁县第一高级中学校联考模拟预测）已知椭圆：的左、右焦点分别为，，过的直线与交于，两点，的周长为8，且点在上．
(1)求椭圆的方程；
(2)设直线与圆：交于C，D两点，当时，求面积的取值范围．
【答案】(1)
(2)
【详解】（1）因为的周长为8，
所以，解得，
将点的坐标代入椭圆方程，得，解得，
所以椭圆E的方程为．

（2）由（1）知圆的方程为，设直线l的方程为，
则圆心到直线l的距离，
由，可得．
设，，联立方程组，
消去x得，
则，，
所以，
设，则，
设，
易知在上单调递增，则在上单调递增，
因为，
所以．

【变式2】（2023春·上海黄浦·高三上海市大同中学校考阶段练习）已知椭圆．
(1)求该椭圆的离心率；
(2)设点是椭圆C上一点，求证：过点P的椭圆C的切线方程为；
(3)若点M为直线l：x=4上的动点，过点M作该椭圆的切线MA，MB，切点分别为，求△的面积的最小值．
【答案】(1)
(2)详见解析；
(3)
【详解】（1）椭圆中，，则，
则，则椭圆的离心率为
（2）当切线斜率存在时，其方程可设为，
由，整理得，
则，则
此时方程的根为，则切点横坐标，
切点纵坐标，
则，，
则切线方程为，整理得；
当切线斜率不存在时，其切点为或，
切线方程为，满足.
综上，点是椭圆C上一点时，
过点P的椭圆C的切线方程为
（3）设，，
则椭圆C在点的切线方程分别为，，
又在两条切线上，则，，
则直线的方程为，即
由整理得，，
则，
则
，
又点M到直线的距离，
则△的面积为
令，则，，
则，
令，，
则恒成立，
则在上单调递增，则
当且仅当即点M坐标为时等号成立，
则△的面积的最小值为.

【变式3】（2023·北京大兴·校考三模）已知椭圆过点，且离心率为.
(1)求椭圆的方程；
(2)直线分别交椭圆于、两点，若线段的中点在直线上，求面积的最大值.
【答案】(1)
(2)
【详解】（1） .
又在椭圆上 .
所以，椭圆方程为.
（2）由已知直线的斜率存在.
设直线方程为，，，
由， 得．
由，得．①
，．

又中点在直线上， 即，
将之代入①得 ，所以．
，
点到直线的距离，
．
设，．
．
时，的最大值为．
题型03双曲线中三角形（四边形）的面积问题（定值）
【典例1】（2023春·上海宝山·高二上海交大附中校考期中）已知双曲线，及直线.
(1)若与有且只有一个公共点，求实数的值；
(2)若与的左右两支分别交于A、B两点，且的面积为，求实数的值.
【答案】(1)或
(2)
【详解】（1）由，消去，得①，
当，即时，方程①有一解，与仅有一个交点（与渐近线平行时）.
当，得与也只有一个交点（与双曲线相切时），
综上得的取值是或；
（2）设交点，由，消去，得，
首先由，得且，
并且，
又因为与的左右两支分别交于A､B两点，
所以，即，解得，
故.
因为直线l与y轴交于点，
所以，
故.
解得或.
因为，所以.
【典例2】（2023·全国·高三专题练习）已知双曲线C：的一条渐近线方程为，焦点到渐近线的距离为1．
(1)求双曲线C的标准方程与离心率；
(2)已知斜率为的直线与双曲线C交于x轴下方的A，B两点，O为坐标原点，直线OA，OB的斜率之积为，求的面积．
【答案】(1)；
(2)
【详解】（1）由题意知焦点到渐近线的距离为，
则
因为一条渐近线方程为，所以，
又，解得，，
所以双曲线的标准方程为，
离心率为．
（2）设直线：，，，
联立
则，
所以，
由
解得（舍）或，
所以，
：，令，得，
所以的面积为，
【典例3】（2023·全国·模拟预测）已知双曲线的离心率为，左、右焦点分别为，，焦距为．点在第一象限的双曲线上，过点作双曲线切线与直线交于点．
(1)证明：；
(2)已知斜率为的直线与双曲线左支交于 两点，若直线，的斜率互为相反数，求的面积．
【答案】(1)证明见解析；
(2)
【详解】（1）解：因为双曲线的离心率为，左、右焦点分别为，，焦距为，
所以，，解得，
所以，双曲线的标准方程为，
因为过点作双曲线切线与直线交于点，故切线的斜率存在，
所以，设，在点的切线方程为，
联立方程得
所以，，即①
因为，代入①式得，解得
所以，在点的切线方程为，
所以点的坐标为，即，
因为，
所以
所以，
（2）解：由题，设直线的方程为，
与双曲线方程联立得，
设，
所以
因为直线，的斜率互为相反数，所以，
所以，
整理得：②
将代入②整理得：③
结合可知时，③式恒成立，
所以，由（1）可知，，，
所以，
所以的面积.
【变式1】（2023·全国·高三专题练习）已知M是平面直角坐标系内的一个动点，直线与直线垂直，A为垂足且位于第一象限，直线与直线垂直，B为垂足且位于第四象限，四边形（O为原点）的面积为8，动点M的轨迹为C.
(1)求轨迹C的方程；
(2)已知是轨迹C上一点，直线l交轨迹C于P，Q两点，直线，的斜率之和为1，，求的面积.
【答案】(1)（）
(2)
【详解】（1）设动点，由题意知M只能在直线与直线所夹的范围内活动.
， ，
动点在右侧，有，同理有，
∵四边形的面积为8，∴，即 ，
所以所求轨迹C方程为（）.
（2）如图，设直线的倾斜角为，斜率为k，直线倾斜角为，则斜率为，
，，在曲线C上，过点T直线与曲线C有两个交点，
则或，同时或，解得或.
，解得或（舍去）.
时，直线的方程为，
联立，消y得：，则或，得.
直线的方程为，
联立，消y得：，则或，得，
，
点Q到直线的距离 ，
.
方法二： ，
，
，则，
.
【变式2】（2023春·湖北荆州·高二统考阶段练习）已知双曲线C：的左，右焦点分别为，，且，都在圆上，连接双曲线C的两个实轴端点、两个虚轴端点组成的菱形的面积为．
(1)求双曲线C的标准方程；
(2)设P是双曲线C与圆在第一象限的交点，求的面积．
【答案】(1)
(2)
【详解】（1）由双曲线方程知：焦点，
∵，都在圆，
∴，解得（负值舍去），
∵连接双曲线C的两个实轴端点、两个虚轴端点组成的菱形的面积为，
∴，得，①
又，②
联立①②，解得，或，，
∵，∴，舍去，∴，，
故双曲线C的标准方程为．
（2）由（1）知：，，
∴是圆的直径，∴，
∴，
∴，
∴．
题型04双曲线中三角形（四边形）的面积问题（最值或范围）
【典例1】（2023春·福建莆田·高二莆田一中校考期中）在平面直角坐标系中，动点到的距离与它到直线的距离之比为2，记的轨迹为曲线.
(1)求曲线的方程；
(2)过的直线交曲线于两点（均位于轴右侧），关于原点的对称点为，求的面积的取值范围.
【答案】(1)
(2)
【详解】（1）设点，
依题意有，
即，
化简得.
（2）设，，
由题意，直线的斜率不为0，设直线的方程为，
联立直线与双曲线的方程，
整理可得，
则，.
由已知可得，，
所以，
所以.
又，
所以.
设，则，且，所以.
，
当时，该式有最小值，
所以的面积的取值范围是.
【典例2】（2023·浙江金华·模拟预测）P是双曲线右支上一点，A，B是双曲线的左右顶点，过A，B分别作直线PA，PB的垂线AQ，BQ，AQ与BQ的交点为Q，PA与BQ的交点为C．
(1)记P，Q的纵坐标分别为，求的值；
(2)记的面积分别为，当时，求的取值范围．
【答案】(1)3
(2)
【详解】（1）由已知条件得：，设PA，PB的斜率分别为，
则QA，QB的斜率分别为，
由即有．
由即有
而，
．
（2）由于，
显然P，Q，B，A四点共圆，
PO为直径，PQ中点为圆心，
又
则，
①，又 ②，
得：，解得．
由，，而．
．
因为，根据单调性，求得
【变式1】（2023·云南昆明·高三昆明一中校考阶段练习）在平面直角坐标系中，点，点.以G为圆心作一个半径为6的圆，点P是圆上一动点，线段AP的垂直平分线与直线GP相交于点Q.
(1)求Q的轨迹方程；
(2)过原点斜率为的直线l交曲线Q于B，C两点，求四边形GBAC面积的最大值.
【答案】(1)
(2)
【详解】（1）如下图所示，
由题意可知点Q在线段AP的垂直平分线，所以，
又点P是圆G上一动点，所以，
所以；
同理，若如下图所示则满足，
所以，Q的轨迹满足，
根据双曲线定义可知，Q点的轨迹是以为左右焦点，实轴长为的双曲线，
可得，；
所以Q的轨迹方程.
（2）如下图所示，
设直线l的方程为，联立整理可得
，解得，不妨设，
所以四边形GBAC面积
又因为，所以，当时等号成立；
即，
所以四边形GBAC面积的最大值为.
【变式2】（2023·高二课时练习）如图，已知双曲线，经过点且斜率为的直线与交于两点，与的渐近线交于两点（从左至右的顺序依次为），其中.
(1)若点是的中点，求的值；
(2)求面积的最小值.
【答案】(1)
(2)
【详解】（1）设
联立直线与双曲线方程，消去得，
由韦达定理可知，
联立直线与其中一条渐近线方程，解得
即，同理可得，
则，
则可知的中点与中点重合.
由于是的中点，所以，解得；
（2）与联立，消去得
由（1）知，.或
由于，
所以，
又到直线的距离，所以
整理得，
令，则，
当，即时，
的最大值为2，所以的最小值为.
【变式3】（2023春·浙江杭州·高三浙江省杭州第二中学校考阶段练习）已知双曲线，其左、右焦点分别为、，上有一点P满足，．
(1)求b；
(2)过作直线l交于B、C，取BC中点D，连接OD交双曲线于E、H，当BD与EH的夹角为时，求的取值范围．
【答案】(1)
(2)
【详解】（1）由题意,，
，，
在中,由余弦定理得，
，
则，即，.
（2）
双曲线，，
设直线BC的方程为，
由，得，即，
由题意，，
设，则，
则，
则，
则，，直线的方程为，
由，得，由题意，解得，
设，则，
当BD与EH的夹角为时，，
则，得，可知，
所以
，
，，，，
所以，
即的取值范围是．
题型05抛物线中三角形（四边形）的面积问题（定值）
【典例1】（2023·内蒙古呼和浩特·统考二模）已知抛物线T：和椭圆C：，过抛物线T的焦点F的直线l交抛物线于A，B两点，线段AB的中垂线交椭圆C于M，N两点．
(1)若F恰是椭圆C的焦点，求的值；
(2)若，且恰好被平分，求的面积．
【答案】(1)
(2)
【详解】（1）在椭圆中，，所以，
由，得．
（2）设直线l：，，，
联立方程，消去x得，
，则，
设的中点，则，，
设，，则直线MN的斜率为，
，，
相减得到，即，
即，解得，
由点G在椭圆内，得，解得，
因为，
所以p值是1，
所以面积．
【典例2】（2023春·湖北孝感·高二统考期中）如图所示，已知直线与抛物线交于两点，且交于点，点的坐标为
(1)求的值；
(2)若线段的垂直平分线与抛物线交于两点，求的面积.
【答案】(1)
(2)
【详解】（1）解：由于点，可得，所以，
所以直线的为，即，
联立方程组，整理得，
设，可得，且，
又由，可得，
所以，即，解得，
所以抛物线的方程为.
（2）解：设中点为，由（1）知，
所以，所以，即，
联立方程组，整理得，易得，
设，可得，
所以，
所以.
【变式1】（2023·陕西安康·统考三模）已知抛物线的焦点为.
(1)求抛物线的方程；
(2)过点的直线与抛物线交于两点，为抛物线上的点，且，，求的面积.
【答案】(1)；
(2)32
【详解】（1）解：由已知可得，解得，
∴拋物线的方程为；
（2）解：如图所示：

设，，，
若轴，由得，，或，，
此时不满足，∴不满足题意；
设直线的方程为，直线的方程为，
将代入抛物线方程得，，
∴， .
将代入抛物线方程得，∴①.
直线的斜率为，同理直线的斜率为.
∵，∴，
∴，即②.
由①②解得，将其代入①可得，
解得或，
当时，直线的方程为，，.
∵，满足，∴， .
∴，
∴.
同理可得，当时，直线的方程为，，，
∵，满足，∴， .
∴，
∴，
∴的面积为32.
【变式2】（2023秋·青海西宁·高二校考期末）设椭圆的四个顶点围成的菱形的面积为4，且点为椭圆上一点.拋物线的焦点与点关于直线对称.
(1)求椭圆及抛物线的方程；
(2)直线与椭圆交于，与拋物线交于（异于原点），若，求四边形的面积.
【答案】(1)椭圆方程为，抛物线的方程为
(2)
【详解】（1）由题可得，解得，所以椭圆方程为，
易得点关于直线对称点为,所以，即，所以抛物线的方程为.
（2）联立方程得，设，
则，
设，联立方程，得，
所以，
因为，所以，解得，
因为，所以，故直线方程为，所以，
点到直线的距离为，点到直线的距离为，
所以四边形的面积.
题型06抛物线中三角形（四边形）的面积问题（最值或范围）
【典例1】（2023·全国·高二专题练习）已知抛物线的顶点为坐标原点，焦点在坐标轴上，设是抛物线上一点．
(1)求抛物线方程；
(2)若抛物线的焦点在x轴上，过点M做两条直线分别交抛物线于A，B两点，若直线与的倾斜角互补，求面积的最大值．
【答案】(1)或
(2)
【详解】（1）若抛物线的焦点在x轴上，设抛物线方程为，
代入，则，即，此时抛物线方程为；
若抛物线的焦点在轴上，设抛物线方程为，
代入，则，即，此时抛物线方程为；
综上，抛物线方程为或；
（2）由（1）可得抛物线方程为
由题可知斜率存在，设直线得方程为：，

则，所以，，则
所以
因为直线与的倾斜角互补，则，
则，所以，整理得：，
所以，化简得
所以，则或
若，则，直线的方程为，此时直线经过点，不符合题意，
故，即直线方程为，且，由图可知直线在上方，所以，即
则点到直线的距离
的面积为令，则
令，则或（舍）
当时，，在上单调递增；当时，，在上单调递减；
所以，即的面积的最大值为.
【典例2】（2023秋·高二单元测试）已知抛物线，点在抛物线上，且点到抛物线的焦点的距离为.
(1)求；
(2)设圆，点是圆上的动点，过点作圆的两条切线，分别交抛物线于两点，求的面积的最大值.
【答案】(1)
(2)
【详解】（1）由题知准线方程为，则，得.
（2）抛物线的方程为，把点代入到抛物线方程，，又，
所以，则点的坐标为，
依题知过点的直线斜率必存在，
(2)若P为C上位于第一象限的任一点，直线l与C相切于点P，连接PF并延长交C于点M，过P点作l的垂线交C于另一点N，求面积S的最小值．
【答案】(1)
(2)
【详解】（1）由已知，直线AB的方程为，设，，
联立，可得，所以，
于是
，所以.
故抛物线C的方程为
（2）如下图，
设，，，切线l的方程为，
则有，，
由M，F，P三点共线，可知，即，
因为，化简可得
由，可得，
因为直线l与抛物线相切，故，故
所以直线PN的方程为：，即，
点M到直线PN的距离为，将代入可得，
联立，消可得，消x可得，，
所以，所以，，
故，
当且仅当时，等号成立，此时，面积S的最小值为

【变式2】（2023春·四川广安·高二四川省广安友谊中学校考阶段练习）已知抛物线C：的焦点为，且点与圆上点的距离的最小值为．
(1)求的值；
(2)若点在圆上，过点做抛物线的两切线，其中是切点，求面积的最大值．
【答案】(1)
(2)
【详解】（1）由题可点的坐标为，
点到圆上的点的距离的最小值为，
解得．
（2）由（1）知，抛物线的方程为，即，则．
设切点，则直线．
联立两方程可得点，
设直线，联立抛物线方程，消去可得：，
则，即，且，
从而可知，
∴，
又点到直线的距离，
∴ ①，
又点在圆上，所以，即，代入①，得，
又．所以当时，∴.