2025高考数学一轮复习讲义(新高考通用版)第06讲：拓展一：基本不等式(学生版+解析)

这是一份2025高考数学一轮复习讲义(新高考通用版)第06讲：拓展一：基本不等式(学生版+解析)，共26页。

TOC \ "1-1" \h \u \l "_Tc20732" 方法一：直接法 PAGEREF _Tc20732 \h 3
\l "_Tc15270" 方法二：凑配法 PAGEREF _Tc15270 \h 4
\l "_Tc21065" 方法三：分离法 PAGEREF _Tc21065 \h 7
\l "_Tc11433" 方法四：换元法 PAGEREF _Tc11433 \h 8
\l "_Tc7201" 方法五：常数代换“1”的代换 PAGEREF _Tc7201 \h 11
\l "_Tc1439" 方法六：消元法 PAGEREF _Tc1439 \h 15
\l "_Tc18022" 方法七：对钩函数 PAGEREF _Tc18022 \h 16
1、基本不等式（一正，二定，三相等，特别注意“一正”，“三相等”这两类陷阱）
①如果，，，当且仅当时，等号成立．
②其中叫做正数，的几何平均数；叫做正数，的算数平均数．
2、两个重要的不等式
①（）当且仅当时，等号成立．
②（）当且仅当时，等号成立．
3、利用基本不等式求最值
①已知，是正数，如果积等于定值，那么当且仅当时，和有最小值；
②已知，是正数，如果和等于定值，那么当且仅当时，积有最大值；
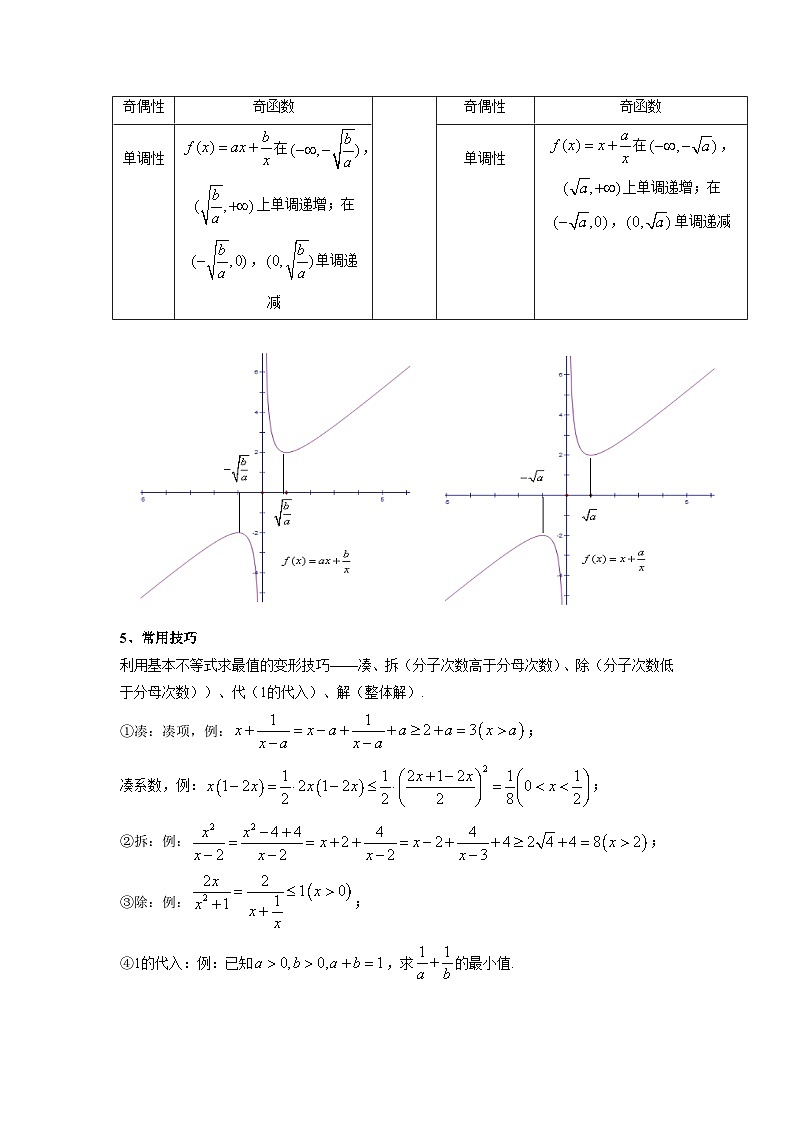
4、对钩函数：
对钩函数是一种类似于反比例函数的一般双曲函数，是形如：（）的函数.由图象得名，又被称为：“双勾函数”、“对号函数”、“双飞燕函数”、“耐克函数”等.

5、常用技巧
利用基本不等式求最值的变形技巧——凑、拆（分子次数高于分母次数）、除（分子次数低于分母次数））、代（1的代入）、解（整体解）.
①凑：凑项，例：；
凑系数，例：；
②拆：例：；
③除：例：；
④1的代入：例：已知，求的最小值.
解析：.
⑤整体解：例：已知,是正数，且，求的最小值.
解析：，即，解得.
基本不等式高频考点方法
方法一：直接法
典型例题
例题1．（2024上·山西长治·高一校联考期末）当时，的最小值为（ ）
A．B．1C．2D．
例题2．（2024上·陕西商洛·高一统考期末）若正数，满足，则的最小值是（ ）
A．10B．20C．100D．200
练透核心考点
1．（2024上·湖南长沙·高一校考期末）若，则的最小值为（ ）
A．B．C．D．2
2．（2024上·贵州六盘水·高一统考期末）已知，则的最大值为 ．
方法二：凑配法
典型例题
例题1．（2024下·河南·高三校联考开学考试）已知，则的最小值为（ ）
A．6B．5C．4D．3
例题2．（2024上·黑龙江哈尔滨·高一统考期末）已知实数，则的（ ）
A．最小值为1B．最大值为1C．最小值为D．最大值为
例题3．（2024上·江苏南通·高一统考期末）函数，的最小值为（ ）
A．B．C．D．
练透核心考点
1．（2024上·湖北·高一校联考期末）已知，则的最小值为
2．（2024上·福建莆田·高一莆田一中校考期末）已知，则的最小值为 .
3．（2024上·福建宁德·高一统考期末），恒成立，则实数的取值范围是 .
方法三：分离法
典型例题
例题1．（2024·全国·高三专题练习）函数的最大值是（ ）
A．2B．C．D．
例题2．（2024·全国·高三专题练习）函数的最小值为 ．
练透核心考点
1．（2023·全国·高一专题练习）函数 的最小值是（ ）
A．B．3C．6D．12
2．（2024·全国·高三专题练习）函数 的最大值为 .
方法四：换元法
典型例题
A．9B．10C．12D．13
例题2．（多选）（2024下·吉林通化·高三梅河口市第五中学校考开学考试）已知，若，则（ ）
A．B．
C．的最大值为D．的最小值为8
例题3．（2024下·全国·高一专题练习）如图所示，在中，点为边上一点，且，过点的直线与直线相交于点，与直线相交于点（，交两点不重合）.若，则 ，若，，则的最小值为 .
练透核心考点
1．（多选）（2024下·湖北·高一湖北省汉川市第一高级中学校联考开学考试）已知正实数，满足，则（ ）
A．B．C．D．
2．（多选）（2024上·云南昭通·高一昭通市第一中学校联考期末）若，，且，则（ ）
A．B．
C．D．
3．（2024上·江西·高一校联考期末）若存在正实数满足，且使不等式有解，则实数的取值范围是 .
方法六：消元法
典型例题
例题1．（2024上·安徽亳州·高一亳州二中校考期末）已知，，则的最小值为（ ）
A．8B．4C．D．
例题2．（2024上·四川眉山·高一统考期末）已知，，且，则的最小值为 ．
练透核心考点
1．（2024上·安徽芜湖·高一统考期末）若实数满足，则的最小值为（ ）
A．1B．C．2D．
2．（2023上·广东东莞·高一统考期末）若、，且，则的最大值为 ．
方法七：对钩函数
典型例题
例题1．（2022上·全国·高一校联考阶段练习）函数的最小值为（ ）
A．2B．C．3D．
例题2．（2023上·江苏苏州·高三统考阶段练习）若不等式对任意恒成立，则实数的取值范围为（ ）
A．B．C．D．
例题5．（2023上·山东·高一校联考期中）若，使得不等式成立，则实数的取值范围是 .
练透核心考点
1．（2023上·海南海口·高一海南华侨中学校考阶段练习）若函数在是增函数，则实数的取值范围是（ ）
A．B．
C．D．
2．（2023上·四川宜宾·高一校考阶段练习）已知函数，若存在，使得，当时，求的最小值为 ．
3．（2024上·山东日照·高一统考期末）已知函数．
(1)求不等式的解集；
(2)若存在，使得不等式成立，求实数的取值范围．
函数
（）
常考对钩函数
（）
定义域
定义域
值域
值域
奇偶性
奇函数
奇偶性
奇函数
单调性
在，上单调递增；在，单调递减
单调性
在，上单调递增；在，单调递减
第06讲：拓展一：基本不等式
目录
TOC \ "1-1" \h \u \l "_Tc20732" 方法一：直接法 PAGEREF _Tc20732 \h 3
\l "_Tc15270" 方法二：凑配法 PAGEREF _Tc15270 \h 4
\l "_Tc21065" 方法三：分离法 PAGEREF _Tc21065 \h 7
\l "_Tc11433" 方法四：换元法 PAGEREF _Tc11433 \h 8
\l "_Tc7201" 方法五：常数代换“1”的代换 PAGEREF _Tc7201 \h 11
\l "_Tc1439" 方法六：消元法 PAGEREF _Tc1439 \h 15
\l "_Tc18022" 方法七：对钩函数 PAGEREF _Tc18022 \h 16
1、基本不等式（一正，二定，三相等，特别注意“一正”，“三相等”这两类陷阱）
①如果，，，当且仅当时，等号成立．
②其中叫做正数，的几何平均数；叫做正数，的算数平均数．
2、两个重要的不等式
①（）当且仅当时，等号成立．
②（）当且仅当时，等号成立．
3、利用基本不等式求最值
①已知，是正数，如果积等于定值，那么当且仅当时，和有最小值；
②已知，是正数，如果和等于定值，那么当且仅当时，积有最大值；
4、对钩函数：
对钩函数是一种类似于反比例函数的一般双曲函数，是形如：（）的函数.由图象得名，又被称为：“双勾函数”、“对号函数”、“双飞燕函数”、“耐克函数”等.

5、常用技巧
利用基本不等式求最值的变形技巧——凑、拆（分子次数高于分母次数）、除（分子次数低于分母次数））、代（1的代入）、解（整体解）.
①凑：凑项，例：；
凑系数，例：；
②拆：例：；
③除：例：；
④1的代入：例：已知，求的最小值.
解析：.
⑤整体解：例：已知,是正数，且，求的最小值.
解析：，即，解得.
基本不等式高频考点方法
方法一：直接法
典型例题
例题1．（2024上·山西长治·高一校联考期末）当时，的最小值为（ ）
A．B．1C．2D．
【答案】C
【分析】根据题意，结合基本不等式，即可求解.
【详解】由，可得，则，
当且仅当时，即时，等号成立，故的最小值为2．
故选：C．
例题2．（2024上·陕西商洛·高一统考期末）若正数，满足，则的最小值是（ ）
A．10B．20C．100D．200
【答案】B
【分析】根据基本不等式求出最值.
【详解】由题意得，当且仅当时，等号成立，
故的最小值是20．
故选：B
练透核心考点
1．（2024上·湖南长沙·高一校考期末）若，则的最小值为（ ）
A．B．C．D．2
【答案】D
【分析】直接根据基本不等式求解即可.
【详解】若，则，
当且仅当，即时取等号，
所以的最小值为.
故选：D.
2．（2024上·贵州六盘水·高一统考期末）已知，则的最大值为 ．
【答案】
【分析】由基本不等式求积的最大值.
【详解】，
由基本不等式可知，
当且仅当时等号成立，即的最大值为.
故答案为：
方法二：凑配法
典型例题
例题1．（2024下·河南·高三校联考开学考试）已知，则的最小值为（ ）
A．6B．5C．4D．3
【答案】D
【分析】根据基本不等式即可求解.
【详解】由于，所以，
由,
（当且仅当时取等号），可得的最小值为3，
故选：D．
例题2．（2024上·黑龙江哈尔滨·高一统考期末）已知实数，则的（ ）
A．最小值为1B．最大值为1C．最小值为D．最大值为
【答案】D
【分析】由基本不等式得出结果.
【详解】因为，
当且仅当即时取等号；
故最大值为，
故选：D.
例题3．（2024上·江苏南通·高一统考期末）函数，的最小值为（ ）
A．B．C．D．
【答案】B
【分析】将函数解析式变形为，利用基本不等式可求得该函数的最小值.
【详解】因为，则，则
，
当且仅当时，即当时，等号成立，
故函数，的最小值为.
故选：B.
练透核心考点
1．（2024上·湖北·高一校联考期末）已知，则的最小值为
【答案】
【分析】利用基本不等式求得正确答案.
【详解】由于，所以，
所以
，
当且仅当时等号成立，
所以的最小值为.
故答案为：
2．（2024上·福建莆田·高一莆田一中校考期末）已知，则的最小值为 .
【答案】8
【分析】利用基本不等式求最值可得答案.
【详解】时，
则，
当且仅当即时等号成立.
故答案为：8.
3．（2024上·福建宁德·高一统考期末），恒成立，则实数的取值范围是 .
【答案】
【分析】利用基本不等式求出，从而得到，求出答案.
【详解】，，
当且仅当，即时，等号成立，
故，解得，
故实数的取值范围是.
故答案为：
方法三：分离法
典型例题
例题1．（2024·全国·高三专题练习）函数的最大值是（ ）
A．2B．C．D．
【答案】C
【分析】化简函数，结合基本不等式，即可求解.
【详解】由题意，函数
又由，当且仅当，即时等号成立，
所以，所以
即函数的最大值是.
故选：C.
例题2．（2024·全国·高三专题练习）函数的最小值为 ．
【答案】
【分析】将函数化为，利用基本不等式求其最小值，注意取值条件即可.
【详解】由，又，
所以，当且仅当，即时等号成立，
所以原函数的最小值为.
故答案为：
练透核心考点
1．（2023·全国·高一专题练习）函数 的最小值是（ ）
A．B．3C．6D．12
【答案】A
【分析】由基本不等式求解，
【详解】
因为 所以 ， (当且仅当 即 时，等号成立
故最小值为，
故选：A
2．（2024·全国·高三专题练习）函数 的最大值为 .
【答案】/
【分析】首先化简可得，由则可以利用基本不等式求最值即可.
【详解】因为，则，
所以
≤，
当且仅当，即时等号成立，
所以的最大值为.
故答案为：.
方法四：换元法
典型例题
例题1．（2023·全国·高一专题练习）函数 的最小值为 ．
【答案】7
【分析】换元转化成基本不等式的形式，利用积为定值即可求和的最小值.
【详解】令，；则

(当且仅当，即时，等号成立)，
故函数 ，的最小值为
故答案为：7
例题2．（2023·全国·高三专题练习）求下列函数的最小值
（1）；
（2）.
【答案】（1）3；（2）10.
【分析】（1）化简整理可得，利用基本不等式，即可求得最小值.
（2）令，整理可得，利用基本不等式，即可求得最小值.
【详解】（1）
∵（当且仅当，即x=1时取等号）
的最小值为3；
（2）令，则，

当且仅当即t=3时取等号
y的最小值为10
练透核心考点
1．（2023上·江西南昌·高一南昌二中校考阶段练习）求函数的最小值．
【答案】9．
【分析】令，则，利用基本不等式计算可得；
【详解】因为，所以，令，所以，
所以，
当且仅当，即时等号成立；
所以函数的最小值为．
2．（2023·全国·高一专题练习）求下列函数的最小值
（1）；
（2）；
（3）.
【答案】（1）3；（2）；（3）10.
【分析】对分式函数利用分离常数法构造基本不等式（对勾函数）的结构，或利用基本不等式（1,、2）或利用函数单调性求最值.
【详解】（1）
∵（当且仅当，即x=1时取“=”）
即的最小值为3；
（2）令，则在是单增，
∴当t=2时，y取最小值；
即y的最小值为
（3）令，则可化为：
当且仅当t=3时取“=”
即y的最小值为10
【点睛】易错点睛：利用基本不等式求最值时，要注意其必须满足的三个条件：
(1)“一正二定三相等”“一正”就是各项必须为正数；
(2)“二定”就是要求和的最小值，必须把构成和的二项之积转化成定值；要求积的最大值，则必须把构成积的因式的和转化成定值；
(3)“三相等”是利用基本不等式求最值时，必须验证等号成立的条件，若不能取等号则这个定值就不是所求的最值，这也是最容易发生错误的地方．
方法五：常数代换“1”的代换
典型例题
例题1．（2024上·浙江杭州·高一浙江省杭州第二中学校考期末）已知，，且，则的最小值为（ ）
A．9B．10C．12D．13
【答案】D
【分析】借助基本不等式中“1”的妙用即可得.
【详解】
，
当且仅当，即时，等号成立.
故选：D.
例题2．（多选）（2024下·吉林通化·高三梅河口市第五中学校考开学考试）已知，若，则（ ）
A．B．
C．的最大值为D．的最小值为8
【答案】ABD
【分析】对于AB：根据题意消去，结合的取值范围分析求解；对于C：根据基本不等式运算求解；对于D：根据“1”的灵活应用结合基本不等式分析求解.
【详解】因为，，则，可得，
对于选项AB：因为，
所以，，故AB正确；
对于选项C：因为，
当且仅当时，等号成立，
所以的最大值为，故C错误；
对于选项D：因为，
当且仅当，即时，等号成立，
所以的最小值为8，故D正确；
故选：ABD.
例题3．（2024下·全国·高一专题练习）如图所示，在中，点为边上一点，且，过点的直线与直线相交于点，与直线相交于点（，交两点不重合）.若，则 ，若，，则的最小值为 .
【答案】
【分析】根据向量的加减运算，以为基底，表示出，和已知等式比较，即可得的值，求得的值；结合已知用表示，结合三点共线可得，将化为，展开后利用基本不等式，即可求得的最小值.
【详解】在中，，，则，
故
，
故；
又，而，，
所以，则，
又三点共线，所以，结合已知可知，
故，
当且仅当，结合，即时，取等号；
即的最小值为，
故答案为：；
【点睛】结论点睛：若，则三点共线.
练透核心考点
1．（多选）（2024下·湖北·高一湖北省汉川市第一高级中学校联考开学考试）已知正实数，满足，则（ ）
A．B．C．D．
【答案】ACD
【分析】根据基本不等式判断选项ABC，消元利用二次函数求最值判断D.
【详解】对A：由及基本不等式得，即，
所以，当且仅当时等号成立，故A正确；
对B：，当且仅当时等号成立，
所以，故B错误；
对C：因为，当且仅当，即时等号成立，
所以即，故C正确；
对D：，其中，所以，故D正确.
故选：ACD
2．（多选）（2024上·云南昭通·高一昭通市第一中学校联考期末）若，，且，则（ ）
A．B．
C．D．
【答案】AC
【分析】A、D选项由基本不等式直接求解即可；B选项将原式平方，结合A的结论即可判断；C选项利用乘“1”法进行求解.
【详解】对于A，若m，，且，则有，
当且仅当时等号成立，A正确；
对于B，，由A可得，故，
所以，故B不正确；
对于C，，
当且仅当时等号成立，故C正确；
对于D，，即（当且仅当时等号成立），故D不正确，
故选：AC.
3．（2024上·江西·高一校联考期末）若存在正实数满足，且使不等式有解，则实数的取值范围是 .
【答案】
【分析】利用基本不等式“1”的妙用求得的最小值，再利用能成立问题得到关于的不等式，解之即可得解.
【详解】因为正实数满足，
所以，
当且仅当，即时，等号成立，
若不等式有解，则，解得或，
则实数m的取值范围是.
故答案为：.
方法六：消元法
典型例题
例题1．（2024上·安徽亳州·高一亳州二中校考期末）已知，，则的最小值为（ ）
A．8B．4C．D．
【答案】A
【分析】首先由条件可得，再变形，最后利用基本不等式，即可求解.
【详解】由，，可得，则
则
，
当，得时，等号成立，
所以的最小值为8.
故选：A
例题2．（2024上·四川眉山·高一统考期末）已知，，且，则的最小值为 ．
【答案】2
【分析】将已知式子适当变形替换，结合基本不等式即可求解.
【详解】由题意，所以，
所以，等号成立当且仅当，
所以的最小值为2.
故答案为：2.
练透核心考点
1．（2024上·安徽芜湖·高一统考期末）若实数满足，则的最小值为（ ）
A．1B．C．2D．
【答案】D
【分析】通过求出，代入所求式消元，运用基本不等式求解即得.
【详解】由可知，则，代入得：，
当时等号成立，即当时，取得最小值.
故选：D.
2．（2023上·广东东莞·高一统考期末）若、，且，则的最大值为 ．
【答案】/0.25
【分析】由题意转换成二次函数的最值来做即可.
【详解】由题意，，所以，
所以等号成立当且仅当，即的最大值为.
故答案为：.
方法七：对钩函数
典型例题
例题1．（2022上·全国·高一校联考阶段练习）函数的最小值为（ ）
A．2B．C．3D．
【答案】B
【分析】结合对勾函数的性质即可求解.
且，，，
故，
所以.
故答案为：.
练透核心考点
1．（2023上·海南海口·高一海南华侨中学校考阶段练习）若函数在是增函数，则实数的取值范围是（ ）
A．B．
C．D．
【答案】A
【分析】变形换元得到，，考虑，和三种情况，结合对勾函数性质得到不等式，求出实数的取值范围.
【详解】，
令，故，，
当，即时，在上单调递增，满足要求，
当，即时，在上单调递增，满足要求，
当，即时，由对勾函数性质得到在上单调递增，
故，解得，
综上，实数的取值范围是.
故选：A
2．（2023上·四川宜宾·高一校考阶段练习）已知函数，若存在，使得，当时，求的最小值为 ．
【答案】
【分析】画出函数的图象，数形结合得到，并根据得到，由对勾函数性质求出最小值，得到答案.
【详解】，
画出其图象如下：
因为存在，使得，在同一坐标系内画出的图象，
故，故，
由于，故令，解得，
由对勾函数性质可得在上单调递增，
故在处取得最小值，最小值为.
故答案为：
3．（2024上·山东日照·高一统考期末）已知函数．
(1)求不等式的解集；
(2)若存在，使得不等式成立，求实数的取值范围．
【答案】(1)
(2)
【分析】（1）解不等式得到，从而求出的解集；
（2）换元后得到对于能成立，利用函数单调性求出，得到答案.
【详解】（1），令，
则原不等式可化为，解得，即
所以，不等式的解集．
（2）当时，令，可得，
原不等式可化为对于能成立，
即可得对于能成立，
由对勾函数性质可知在上单调递增，所以，
因此只需即可，得；
即的取值范围是．
函数
（）
常考对钩函数
（）
定义域
定义域
值域
值域
奇偶性
奇函数
奇偶性
奇函数
单调性
在，上单调递增；在，单调递减
单调性
在，上单调递增；在，单调递减