湘教版（2024）七年级上册（2024）3.1 等量关系和方程完美版教学ppt课件

这是一份湘教版（2024）七年级上册（2024）3.1 等量关系和方程完美版教学ppt课件，文件包含341一元一次方程的应用1课件pptx、341一元一次方程的应用1教学设计docx、第3章一次方程组大单元教学设计docx等3份课件配套教学资源，其中PPT共30页， 欢迎下载使用。

1.通过本节课理解行程问题，能借助图示法分析出行程问题中的路程、速度和时间之间的等量关系，正确列出一元一次方程解决行程问题。2.经历运用方程解决实际问题的过程，体会方程是刻画现实世界的有效数学模型。3.培养分析问题、解决实际问题、综合归纳整理的能力，能运用方程解决生活中的实际问题，获得解决问题的经验。
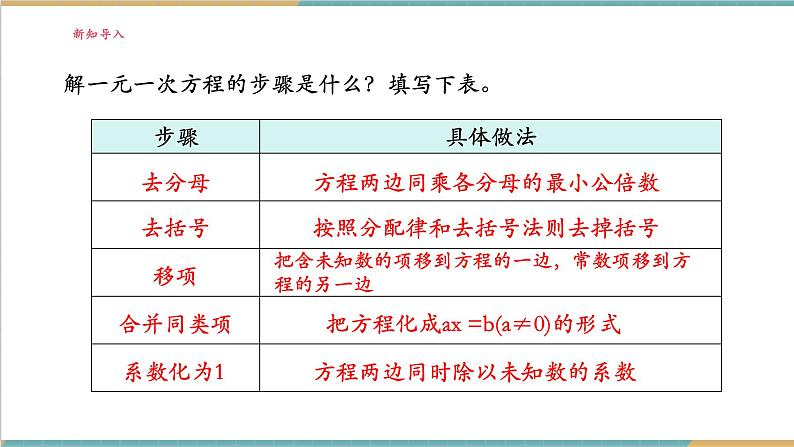
解一元一次方程的步骤是什么？填写下表。
方程两边同乘各分母的最小公倍数
按照分配律和去括号法则去掉括号
把含未知数的项移到方程的一边，常数项移到方程的另一边
把方程化成ax =b(a≠0)的形式
方程两边同时除以未知数的系数
思考：一艘轮船在甲、乙两个码头之间航行，顺水航行时需 4 h，逆水航行时需5 h. 已知水流速度为2 km/h，则轮船在静水中的航行速度是多少？
在这个问题中有如下等量关系：（1） 轮船顺水航行的速度=_________________________________
轮船在静水中的航行速度+水流速度
（2） 轮船逆水航行的速度=_________________________________
轮船在静水中的航行速度-水流速度
（3） 轮船顺水航行的路程=轮船逆水航行的路程.
设轮船在静水中的航行速度为 x km/h，则根据等量关系（1）（2）分别可得，轮船顺水航行的速度为 km/h，逆水航行的速度为_________km/h.
又路程=____________，于是根据等量关系（3），可列出方程：
4（x + 2）= 5（x - 2）.
解得 x = 18.
因此，轮船在静水中的航行速度为18 km/h.
【总结归纳】一元一次方程是一种重要的数学模型 . 利用等量关系建立一元一次方程，可以帮助我们解决一些实际问题.找等量关系时，可以通过画图、列表、演示等多种方法，这些也是列方程解应用题的有效方法和手段.
【例1】某房间里有 4 条腿的椅子和 3 条腿的凳子共 16 把，如果椅子腿数与凳子腿数的和为60，试问：有几张椅子和几把凳子？
你能找出题目中的等量关系吗？
椅子数 + 凳子数 = 16，
椅子腿数 + 凳子腿数 = 60.
解：设有x张椅子，则有（16 - x）把凳子.
根据题意，得4x + 3（16 - x）= 60.
解得 x = 12.
因此，凳子有16 - 12 = 4（把）.
答：有12张椅子，4把凳子.
【归纳总结】设未知数的常见方法：设未知数分为“直接设”和“间接设”两种，“直接设”较为常用，即求什么就设什么为未知数，当直接设未知数解决问题有困难时，可以间接设未知数，
【例2】刺绣是我国民间传统手工艺之一. 我国刺绣主要有湘绣、苏绣、蜀绣、粤绣四大类 . 若刺绣一件作品，甲单独绣需要 15 天才能完成，乙单独绣需要 12 天才能完成 . 现在甲先单独绣 1 天，接着乙又单独绣 4天，剩下的工作由甲、乙两人合绣. 试问：再合绣多少天可以完成这件作品？
因为甲先单独绣 1 天，乙又单独绣 4天，若甲、乙两人合绣x天，则甲共绣了________天，乙共绣了________天.
甲完成的工作量+乙完成的工作量=总工作量.
解：设剩下的工作由甲、乙两人合绣x天可以完成，则根据题意，得
解得 x = 4.
答：甲、乙两人再合绣4天就可以完成这件作品.
做一做：结合上述 3个实例，用流程图总结用一元一次方程解决有关实际问题的具体步骤，并与同学交流.
【知识技能类作业】必做题：
1.端午节买粽子，每个肉粽比素粽多1元，购买10个肉粽和5个素粽共用去70元，设每个肉粽x元，则可列方程为(　　)A．10x＋5(x－1)＝70B．10x＋5(x＋1)＝70C．10(x－1)＋5x＝70D．10(x＋1)＋5x＝70
2.笼中有鸡兔共25只，且有60只脚，设鸡有x只，则可列方程为(　　)A．2x＋4x＝60B．2x＋2(25－x)＝60C．4x＋4(25－x)＝60D．2x＋4(25－x)＝60
3.A，B两地相距37 km，甲从A地步行到B地，乙从B地步行到A地，甲比乙晚出发1 h，乙出发5 h后两人在途中相遇，已知甲每小时比乙多走1 km，设甲每小时走x km.依题意得方程为(　　)A．4x＋5(x－1)＝37 B．5x＋4(x－1)＝37C．4x＋5(x＋1)＝37 D．5x＋4(x＋1)＝37
4.A，B两地相距28 km，甲、乙两人分别从A，B两地同时出发，相向而行，经过t h相遇．若甲的步行速度是4 km/h，乙的步行速度是3 km/h.从出发到相遇的过程中，下列说法不正确的是(　　)A．甲、乙所走路程之和为28 kmB．甲、乙步行所用时间相同C．甲、乙所走路程相同D．步行时间t满足方程4t＋3t＝28
【知识技能类作业】选做题：
5.幻方，最早源于我国，古人称之为纵横图．如图所示的幻方中，各行、各列及各条对角线上的三个数字之和均相等，则图中a的值为________．
6.我国元朝朱世杰所著的《算学启蒙》(1299年)记载：“良马日行二百四十里，驽马日行一百五十里．驽马先行六日，问良马几何追及之．”翻译为：跑得快的马每天走240里，跑得慢的马每天走150里．慢马先走6天，快马几天可以追上慢马？则快马追上慢马的时间为(　　)A．10天 B．15天 C．20天 D．25天
7.已知A，B两地相距450千米，甲、乙两车分别从A，B两地同时出发，已知甲车速度为115千米/时，乙车速度为85千米/时．(1)两车同向而行，快车在后，求经过几小时快车追上慢车？
解：设经过x小时快车追上慢车．列方程为115x－85x＝450，解得x＝15.答：经过15小时快车追上慢车．
7.(2)两车相向而行，求经过几小时两车相距50千米？
解：设经过a小时两车相距50千米．两种情况：①相遇前两车相距50千米，根据题意得115a＋85a＋50＝450，解得a＝2；②相遇后两车相距50千米，根据题意得115a＋85a－50＝450，解得a＝2.5.答：经过2小时或2.5小时两车相距50千米．
用一元一次方程解决有关实际问题的具体步骤:
1.甲、乙两人从相距60 km的两地同时出发，相向而行，甲步行每小时走5 km，乙骑自行车，3 h后相遇，则乙的速度为(　　)A．5 km/h B．10 km/h C．15 km/h D．20 km/h
2.小明、小刚两人从同一地点出发，如果小明先出发1 h后，小刚从后面追赶，那么当小刚追上小明时，下面说法正确的是(　　)A．小刚比小明多走了1 hB．小刚、小明所走的路程相等C．小刚、小明所用的时间相等D．小刚走的路程比小明多
3.一艘轮船在长江A，B两个码头之间航行，顺水航行需要4 h，逆水航行需要5 h，如果船在静水中的航速是18 km/h，那么水的流速是多少？
解：设水的流速为x km/h，根据题意，可得4(18＋x)＝5(18－x)，解得x＝2.答：水的流速是2 km/h.
4.甲、乙两人在环形跑道上跑步，已知环形跑道长400 m，乙每秒跑6 m，甲每秒跑8 m．如果甲在乙前面8 m处同时同向出发，那么经过________s两人首次相遇．
5.某社区需要进行绿化改造，现有甲、乙两个绿化工程队可供选择，已知甲队每天能完成的绿化改造面积比乙队多200平方米，甲队与乙队合作一天能完成800平方米的绿化改造面积. 甲、乙两工程队每天各能完成多少平方米的绿化改造面积？