山东省济南市槐荫区2024-2025学年九年级上学期11月期中考试数学试卷

这是一份山东省济南市槐荫区2024-2025学年九年级上学期11月期中考试数学试卷，共16页。试卷主要包含了11），已知，则的值是，已知在中，，则的值为，一次函数与二次函数的图象可能是等内容，欢迎下载使用。

本试题分试卷和答题卡两部分．第Ⅰ卷共2页，满分为40分；第Ⅱ卷共6页，满分为110分．本试题共8页，满分为150分．考试时间为120分钟．
答卷前，请考生务必将自己的姓名、准考证号、座号、考试科目涂写在答题卡上，并同时将考点、姓名、准考证号、座号填写在试卷规定的位置．考试结束后，将试卷、答题卡一并交回．本考试不允许使用计算器．
第Ⅰ卷（选择题共40分）
注意事项：
第Ⅰ卷为选择题，每小题选出答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑；如需改动，用橡皮擦干净后，再选涂其他答案标号．答案写在试卷上无效．
一、选择题（本大题共10个小题，每小题4分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．）
1．已知，则的值是（ ）
A．B．C．D．
2．已知在中，，则的值为（ ）
A．B．C．D．
3．若反比例函数的图象在第二、四象限，则的取值范围是（ ）
A．B．C．D．
4．如图是某位同学用带有刻度的直尺在数轴上作图的方法，若图中的虚线相互平行，则点表示的数是（ ）
4题图
A．B．2C．D．5
4题图
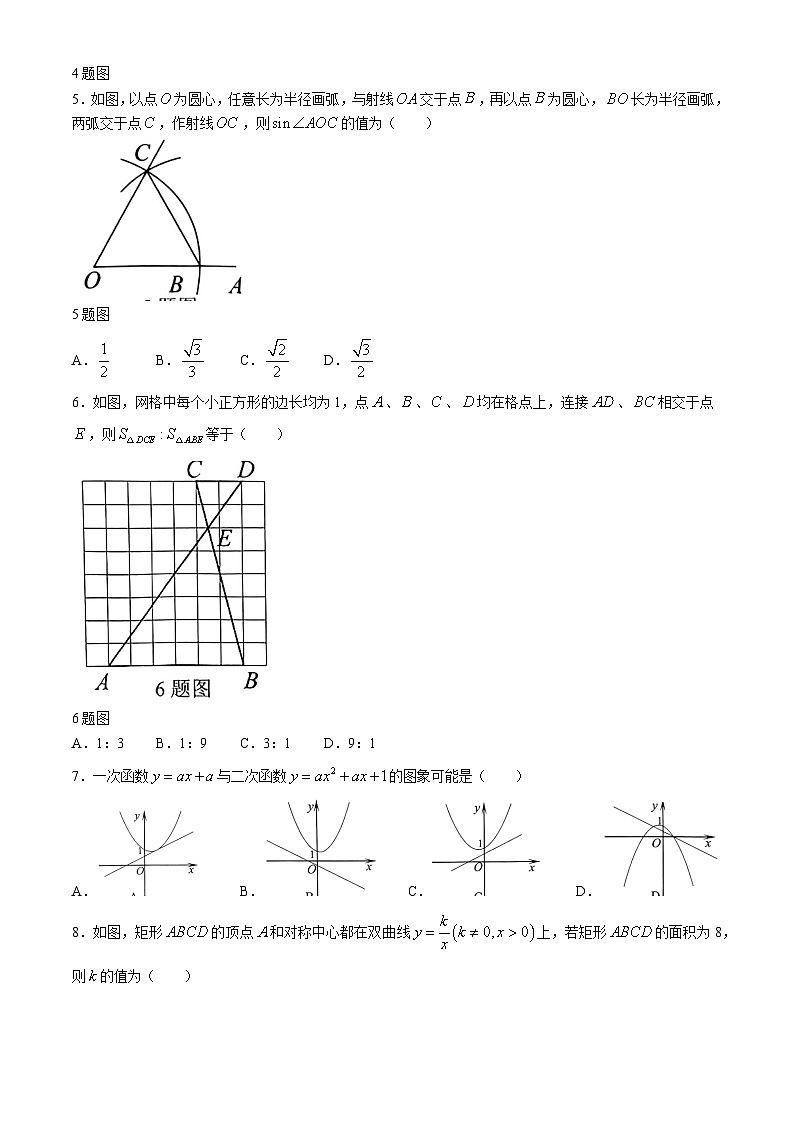
5．如图，以点为圆心，任意长为半径画弧，与射线交于点，再以点为圆心，长为半径画弧，两弧交于点，作射线，则的值为（ ）
5题图
A．B．C．D．
6．如图，网格中每个小正方形的边长均为1，点、、、均在格点上，连接、相交于点，则等于（ ）
6题图
A．1：3B．1：9C．3：1D．9：1
7．一次函数与二次函数的图象可能是（ ）
A．B．C．D．
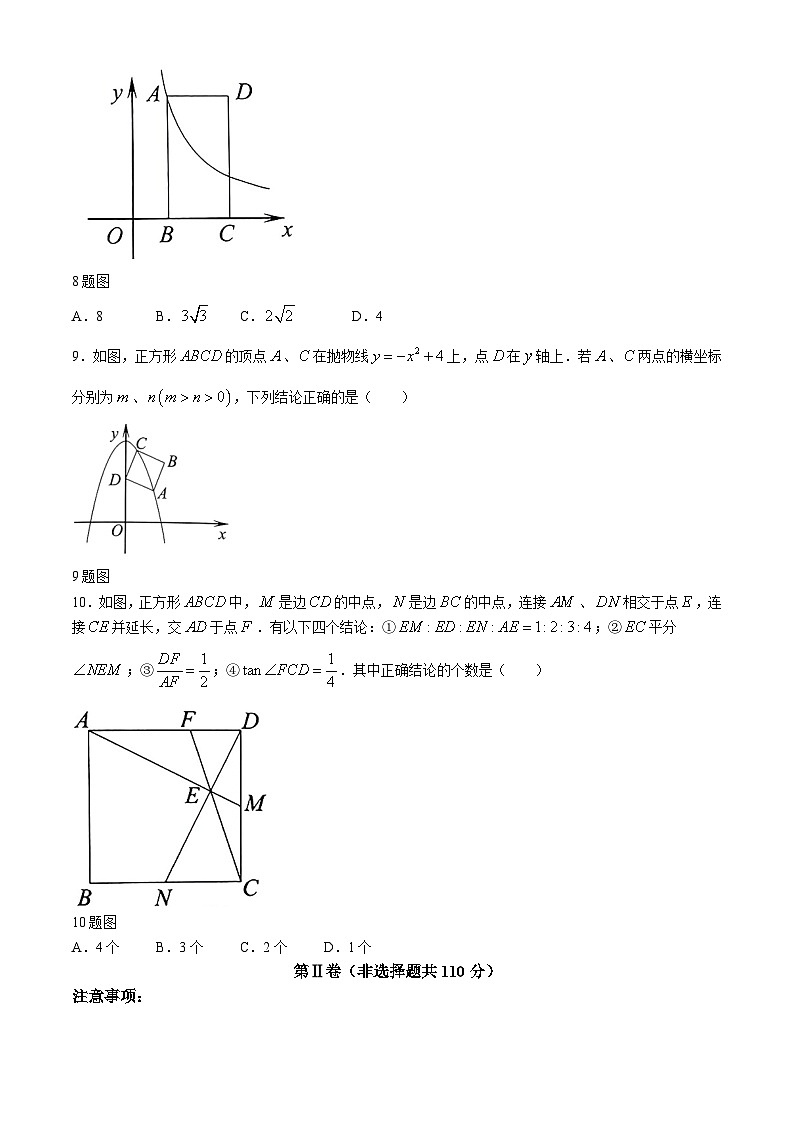
8．如图，矩形的顶点和对称中心都在双曲线上，若矩形的面积为8，则的值为（ ）
8题图
A．8B．C．D．4
9．如图，正方形的顶点、在抛物线上，点在轴上．若、两点的横坐标分别为、，下列结论正确的是（ ）
9题图
10．如图，正方形中，是边的中点，是边的中点，连接、相交于点，连接并延长，交于点．有以下四个结论：①；②平分；③；④．其中正确结论的个数是（ ）
10题图
A．4个B．3个C．2个D．1个
第Ⅱ卷（非选择题共110分）
注意事项：
所有答案必须用0.5毫米的黑色签字笔（不得使用铅笔和圆珠笔）写在答题卡各题目指定区域内（超出方框无效），不能写在试卷上，不能使用涂改液、修正带等．
不按以上要求作答，答案无效．
二、填空题（本大题共5个小题．每小题4分，共20分．把答案填在答题卡的横线上．）
11．已知直线与双曲线的一个交点坐标为（2，4），则它们的另一个交点坐标是_____．
12．抛物线的顶点坐标为_____．
13．如图，直线与双曲线相交于点和点，则不等式的解集为_______．
13题图
14．如图，在正方形中，取的中点，连接，延长至点，使，以线段为边作正方形，点在线段上，则的值是_____．
14题图
15．如图，反比例函数的图象经过点（－1，－4），点是该图象第一象限分支上的动点，连接并延长交另一分支于点，以为对角线作菱形，使，顶点在第四象限，与轴交于点，连接．在点的运动过程中，当平分时，点的坐标是______．
15题图
三、解答题（本大题共10个小题，共90分．解答应写出文字说明，证明过程或演算步骤．）
16．（本小题满分7分）
已知，求的值．
17．（本小题满分7分）
如图，在正方形网格中，每个小正方形的边长均为1，其顶点称为格点，和的顶点都在格点上，与相似吗？请说明理由．
17题图
18．（本小题满分7分）
如图，在中，，求的长．
18题图
19．（本小题满分8分）
在如图所示的平面直角坐标系中，的顶点坐标分别为、、与是以点为位似中心的位似图形．
19题图
（1）在图中标出位似中心的位置，并写出点的坐标；
（2）以原点为位似中心，在位似中心的同侧作出的位似图形，使它与的位似比为2：1，并写出点的对应点的坐标；
（3）的内部一点的坐标为（a，b），写出点在中的对应点的坐标．
20．（本小题满分8分）
在公元前2世纪，中国就制成了世界上最早的潜望镜，西汉初年成书的《淮南万毕术》中有这样的记载：取大镜高悬，悬水盆于其下，则见四邻矣．如图1所示．
潜望镜的工作原理主要是利用光的反射，在图2中，、、三点共线，于点，入射角（入射角等于反射角），米，求的长．
20题图
21．（本小题满分9分）
如图，为上一点，．
21题图
（1）求证：；
（2）若平分，求的长．
22．（本小题满分10分）
心理学家研究发现，一般情况下，一节课40分钟，学生的注意力随教师讲课的变化而变化．开始上课时，学生的注意力逐步增强，中间有一段时间学生的注意力保持较为理想的稳定状态，随后学生的注意力开始分散．经过实验分析可知，学生的注意力指标数随时间（分钟）的变化规律如图所示（其中、分别为线段，为双曲线的一部分）．
22题图
（1）分别求出学生注意力增强阶段和分散阶段的函数关系式；
（2）开始上课后第5分钟时与第30分钟时相比较，哪一时刻学生的注意力更集中？
（3）一道数学竞赛题，需要讲19分钟，为了效果较好，要求学生的注意力指标数最低达到36，那么经过适当安排，老师能否在学生注意力达到所需的状态下讲解完这道题目？若能，最好第几分钟开始讲；若不能，说明理由．
23．（本小题满分10分）
已知，抛物线与轴交于、两点，与轴交于点．
（1）求点、、的坐标；
（2）过点作交抛物线于点，求四边形的面积；
（3）在线段上是否存在一点，使的周长最小？若存在，请求出点的坐标；若不存在，请说明理由．
23题图
24．（本小题满分12分）
如图，已知直线与双曲线在第一象限的交点为点．
24题图24题备用图
（1）求点的坐标和反比例函数的解析式；
（2）将点绕点逆时针旋转至点，求直线的函数解析式；
（3）在（2）的条件下，若点是射线上的一个动点，过点作轴的平行线，交双曲线的图象于点，交轴于点，且，求点的坐标．
25．（本小题满分12分）
【问题情境】
（1）古希腊著名数学家欧几里得在《几何原本》中提出了射影定理，又称．欧几里得定理．：在直角三角形中，斜边上的高是两条直角边在斜边射影的比例中项，每一条直角边又是这条直角边在斜边上的射影和斜边的比例中项．
其符号语言是：如图1，在Rt中，，垂足为，则：①，②，③；请你证明定理中的结论③．
【结论运用】
（2）如图2，正方形的边长为6，点是对角线、的交点，点在上，过点作，垂足为，连接．
①求证：；
②若，求的长．
（3）如图3，正方形的边长为6，点是对角线、的交点，点是上一动点，过点作，垂足为，连接，取的中点，连接，当点在上运动时，是否存在最小值，若存在，请直接写出最小值．若不存在，请说明理由．
25题图
九年级期中数学试题参考答案与评分标准
一、选择题
二、填空题
11．（－2，－4）12．（－2，3）13．或
14．15．
三、解答题
16．解：令，，
，，
，，
．
17．解：与相似，
理由如下：，，
，，
，，
，．
18．解：过点作交于点，
，，，
，，
，，
，，
，，，
．
19．解：（1）如图，点即为所求，；
（2）如图，即为所求，；
（3）根据位似图形的性质可知，点的对应点坐标为（2a，2b）．
20．解：，（入射角等于反射角），，
，，
，，
，，，
作交于点，，
，，
，，
（米），
即的长为米．
21．（1）证明：，
，又，．
（2）解：平分，，
由（1）知，，，
又，，
，即，．
22．解：（1），
设直线的解析式为，
将、两点代入得：解得
注意力增强阶段函数关系式为．
设双曲线的解析式为，将代入得
分散阶段的函数关系式为．
（2）当时，；
当时，；
，时学生注意更集中．
（3）能，理由如下：
当时，令，得；
令，得，
老师能在学生注意力达到所需的状态下讲解完这道题目，最好在第8分钟开始讲．
23．解：（1）当时，，
解得；
点坐标为点坐标为（1，0）；
当时，，
点坐标为（0，－1）．
（2），直线解析式：；设直线的解析式为：，把代入得：
；
则直线解析式为：，
联立解析式有：
解得，；
点坐标为（2，3）；
．
（3）存在．
延长到点，使，过点作轴于点，连接，则与的交点即为点．
，与关于对称．
，．
，
，点坐标为（－2，1）；直线的解析式为；
联立方程组解方程组可得点的坐标为；
在线段上存在一点，使的周长最小．
24．解：（1）点在直线上，，，，
将点代入，，；
（2）根据题意，找出点的位置，过点作轴于点，过点作于点，如图：
，
，，
由旋转可知，，，
，，
设直线的解析式，将点代入得，
直线的解析式为：；
（3）如图，，
，
，
即，即，
设点的横坐标为，由（1）可知反比例函数的解析式为：，
，
，，
解得或；
点的坐标为或．
25．解：（1）证明：，，
，，
，
，；
（2）①证明：四边形为正方形，
，，
，，
，即，
，；
②在中，，
，；
在中，，
，，
即，．
（3）存在．．
题号
1
2
3
4
5
6
7
8
9
10
答案
B
A
D
C
D
B
C
D
A
B