河北省张家口市张北县2023-2024学年八年级上学期期中数学试题

这是一份河北省张家口市张北县2023-2024学年八年级上学期期中数学试题，共10页。试卷主要包含了如图，，，，，则等内容，欢迎下载使用。
数学（人教版）
本试卷共8页，总分120分。考试时间120分钟
注意事项：1.仔细审题，工整作答，保持卷面整洁.
2.考生完成试卷后，务必从头到尾认真检查一遍.
一、选择题（本大题共16个小题，共38分，1—6小题各3分，7—16小题各2分，在每小题给出的四个选项中，只有一项是符合题目要求的）
1.如图，在电线杆上拉两条钢筋，来加固电线杆，这是利用三角形的（）
A.稳定性B.灵活性C.对称性D.全等性
2.下列多边形的内角和最大的是（）
A.B.C.D.
3如图，，，要根据“HL”判定，则需添加的条件是（）
A.B.C.D.
4.将一副含30°，45°的三角板按图中的方式放置，则（）
A.10°B.15°C.20°D.30°
5.如图，在方格纸中已有两个方格被涂黑，再涂黑一个方格，使被涂黑的部分构成轴对称图形，则被涂黑的方格不可能是（）
A.①B.②C.③D.④
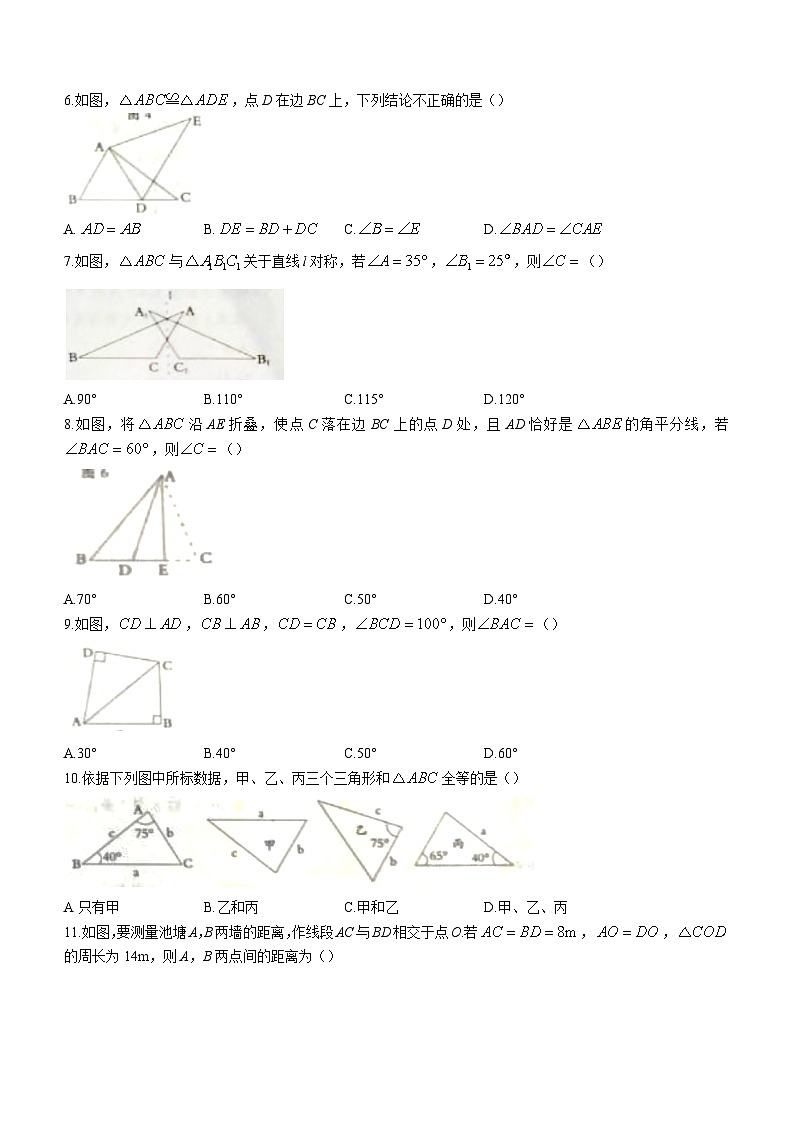
6.如图，，点D在边BC上，下列结论不正确的是（）
A.B.C.D.
7.如图，与关于直线l对称，若，，则（）
A.90°B.110°C.115°D.120°
8.如图，将沿AE折叠，使点C落在边BC上的点D处，且AD恰好是的角平分线，若，则（）
A.70°B.60°C.50°D.40°
9.如图，，，，，则（）
A.30°B.40°C.50°D.60°
10.依据下列图中所标数据，甲、乙、丙三个三角形和全等的是（）
A只有甲B.乙和丙C.甲和乙D.甲、乙、丙
11.如图，要测量池塘A，B两墙的距离，作线段AC与BD相交于点O.若，，的周长为14m，则A，B两点间的距离为（）
A.6mB.8mC.10mD.12m
12.如图，AD，DE，EF分别是，，的中线，若，则（）
A.4B.8C.16D.32
13.如图，直线l与线段AB交于点O，点P在直线l上，且.小明说：“直线l是AB的垂直平分线.”小亮说：“需再添加一个条件，小明的结论才正确.”下列判断正确的是（）
A.小明说的对B.小亮说的对，可添条件为“”
C.小亮说的对，可添条件为“”D.两人说的都不对
14.如图，在中，，依据尺规作图痕迹，下列判断正确的是（）
结论Ⅰ：；结论Ⅱ：.
A.Ⅰ，Ⅱ都对B.Ⅰ对，Ⅱ错C.Ⅰ错，Ⅱ对D.Ⅰ，Ⅱ都错
15将长分别为3，4.6，8的木棍用4颗螺丝按如图所示的方式安在一起，且相邻两木根之间的夹角均可调整，则任意两颗螺丝的距离的最大值是（）
A.8B.10C.11D.14
16.题目：“如图，，，，点P，Q分别在AB，BC上，且，当BP为何值时，与全等.”对于其答案，甲答：，乙答：.丙答：，则正确的是（）
A只有甲答的对B.甲、丙答案合在一起才完整
C.乙、丙答案合在一起才完整D.三人答案合在一起才完整
二、填空题（本大题共3个小题，共10分.17小题2分，18—19小题各4分，每空2分）
17.正八边形的每个外角度数为______.
18.图是雨伞的截面示意图，伞骨，D，E分别是AB，AC的中点，DM，EM是连接弹簧和伞骨的支架，且.
（1）与是否全等？______（填“是”或“否”）；
（2）若，，则的度数为______.
19.已知点在平面直角坐标系上，规定：点A先向右平移1个单位长度后，再沿x轴翻折得到点为第1次变换；点沿y轴翻折得到点为第2水变换；点先向右平移1个单位长度后，再沿x轴翻折得到点为第3次变换；…依此规律进行下去.
（1）点的坐标为______.
（2）点的坐标为______.
三、解答题（本大题共7个小题，共2分，解答应写出文字说明、证明过程或演算步骤）
20.（本小题满分9分）
如图1，已知.
图1图2
（1）在图中作关于直线AC的对称图形；
（2）在（1）的条件下，在图2中，用尺规作，使，，；（不写作法，保留作图痕迹）
（3）在（2）的条件下，作的尺规作图依据是______（填“SSS”“SAS”或“AAS”）.
21.（本小题满分9分）
如图，在中，，，DE是AC的垂直平分线，连接AD.
（1）求的度数；
（2）若，，求的周长.
22.（本小题满分9分）
A和B分别是两个多边形，阅读A和B的对话，完成下列各小题.
（1）嘉嘉说：“因为B的边数比A多，所以B的外角和比A的大，”判断嘉嘉的说法是否正确？并说明理由；
（2）设A的边数为
①若，求x的值；
②淇淇说：“无论n取何值，x的值始终不变.”请用列方程的方法说明理由.
23.（本小题满分10分）
如图是嘉淇荡秋千的示意图，静止时秋千位于点A处，荡秋千过程中，秋千荡到点C时，测得点C到OA的距离CG为2.2m，秋千荡到点B时，测得点B到OA的距离BF为18m，且.
（1）与全等吗？请说明理由；
（2）求GF的长.
24.（本小题满分10分）
如图，在中，，，D，E是BC上的两点，且，与关于直线AD对称，连接EF.
（1）求证；
（2）求的度数：
（3）连接BF，FC，则的度数为______.
25.（本小题满分12分）
如图，在中，BD平分，交AC于点D，动点E在射线BD上（不与点D重合），过点E作交线段AC于点F（不与点A，C重合），的平分线所在的直线与射线BD交于点G.
备用图
（1）当点E在线段BD上时.
①若，，的度数为______；的度数为______；
②求证；
（2）当点E在线段BD的延长线上时，直接写出与之间的数量关系.
26.（本小题满分13分）
在的平分线上取点P，作，垂足为H，动点M，N分别在直线BC，射线OA上，且.
图1图2备用图
（1）如图1，当点M在线段OH上时，作.
①求证；
②求的度数；
（2）如图2，当点M在HO延长线上时.
①的度数为______；
②求OM，OH，ON之问的数量关系；
（3）在满足（2）中①的度数不变的条件下，当点M在射线OH上，点N在射线OA上时，直接写出OM，MH，ON之间的数量关系.
河北省2023—2024学年八年级第一学期第二次学情评估
数学（人教版）参考答案
评分说明：
1.本答案仅供参考，若考生答案与本答案不一致，只要正确，同样得分.
2.若答案不正确，但解题过程正确，可酌情给分.
一、（1—6小题每题3分，7—16小题每题2分，共38分）
二、（17小题2分，18—19小题各4分，每空2分，共10分）
17.45°18.（1）是；（2）30°19.（1）；（2）
三、20.解：
（1）如图；（3分）（2）如图；（4分）
（3）SSS.（2分）
21.解：（1）∵，，
∴.
∵DE是AC的垂直平分线，∴，
∴；（5分）
（2）∵DE是AC的垂直平分线，∴，
∴的周长为.（4分）
22.解：（1）嘉嘉的说法不正确；（1分）
理由：多边形的外角和始终为360°，与多边形的边数无关；（2分）
（2）①，解得，即x的值为2；（3分）
②，整理得，解得.
∴无论n取何值，x的值始终不变.（3分）
23.解：（1）与全等；（2分）
理由：由题意可得，.
∵，，
∴，，∴.
在与中，∴；（4分）
（2）∵，∴，，
∴，即GF的长为0.4m.（4分）
24.解：（1）∵与关于直线AD对称，∴，.
∵，∴.
∵，，∴.
在与中，∴；（5分）
∵与关于直线AD对称，∴.
∵，∴，
∴；（3分）
（3）45°.（2分）
25.解：（1）①20°；（2分）50°；（3分）
②证明：∵BD平分，∴.
∵，∴，.
∵FG平分，∴，
∴；（5分）
（2）.（2分）
【精思博考：如图，点E在线段BD的延长线上.∵BD平分，∴.
∵，∴，，
∴.
∵FH平分，∴，
∴】
26.解：（1）①∵OP是角平分线，，，∴，.
在与中，∴；（3分）
②由（1）①可知，∴，
∴，即，
∴.
∵在四边形GPHO中，
，，
∴，即；（3分）
（2）①180°；（2分）
②如图1，过点P作于点Q.
图1
∵OP是角平分线，，，∴，.
在与中，∴，∴.
在与中，∴，∴，
∴；（3分）
（3）.（2分）
【精思博考：如图2，当点M在线段OH上时，与（2）中②同理可得，，
∴；
如图3，当点M在OH的延长线上时，与（2）中②同理可得，，
∴】
图2图3题号
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
答案
A
D
B
B
D
C
D
A
B
C
A
C
C
A
B
B