辽宁省大连市沙河口区2024-2025学年九年级上学期11月期中数学试题

这是一份辽宁省大连市沙河口区2024-2025学年九年级上学期11月期中数学试题，共19页。试卷主要包含了选择题，四象限，解答题等内容，欢迎下载使用。
1．（3分）关于二次函数y＝﹣3（x﹣1）2+2，下列说法正确的是（ ）
A．开口向上B．对称轴是直线x＝﹣1
C．有最小值2D．顶点坐标是（1，2）
2．（3分）点（﹣1，4）在反比例函数y＝的图象上，则下列各点在此函数图象上的是（ ）
A．（4，﹣1）B．（﹣，1）C．（﹣4，﹣1）D．（，2）
3．（3分）平面内，若⊙O的半径为，OP＝2，则点P在（ ）
A．圆内B．圆上
C．圆外D．圆内或圆外
4．（3分）将抛物线y＝﹣x2向右平移2个单位，再向上平移2个单位，则所得的抛物线的函数表达式为（ ）
A．y＝﹣（x+2）2B．y＝﹣（x+2）2+2
C．y＝﹣（x﹣2）2+2D．y＝﹣（x﹣2）2
5．（3分）反比例函数y＝﹣，下列说法不正确的是（ ）
A．图象经过点（1，﹣3）
B．图象位于第二、四象限
C．图象关于直线y＝x对称
D．y随x的增大而增大
6．（3分）如图，BC是⊙O的弦，OA⊥BC，∠AOB＝55°，则∠ADC的度数是（ ）
A．25°B．55°C．45°D．27.5°
7．（3分）已知抛物线y＝ax2﹣2ax﹣a+1的顶点在x轴上，则a的值是（ ）
A．﹣2B．C．﹣1D．1
8．（3分）如图，一个底部呈球形的烧瓶，球的半径为5cm，瓶内液体的最大深度CD＝2cm，则截面圆中弦AB的长为（ ）
A．B．6cmC．8cmD．8.4cm
9．（3分）如图是嘉淇某次实验中的情形，左侧每个钩码的质量均为2kg，杠杆总长30cm，其余数据如图所示，此时杠杆处于平衡状态，则y与x的函数图象可能是（ ）
A．B．
C．D．
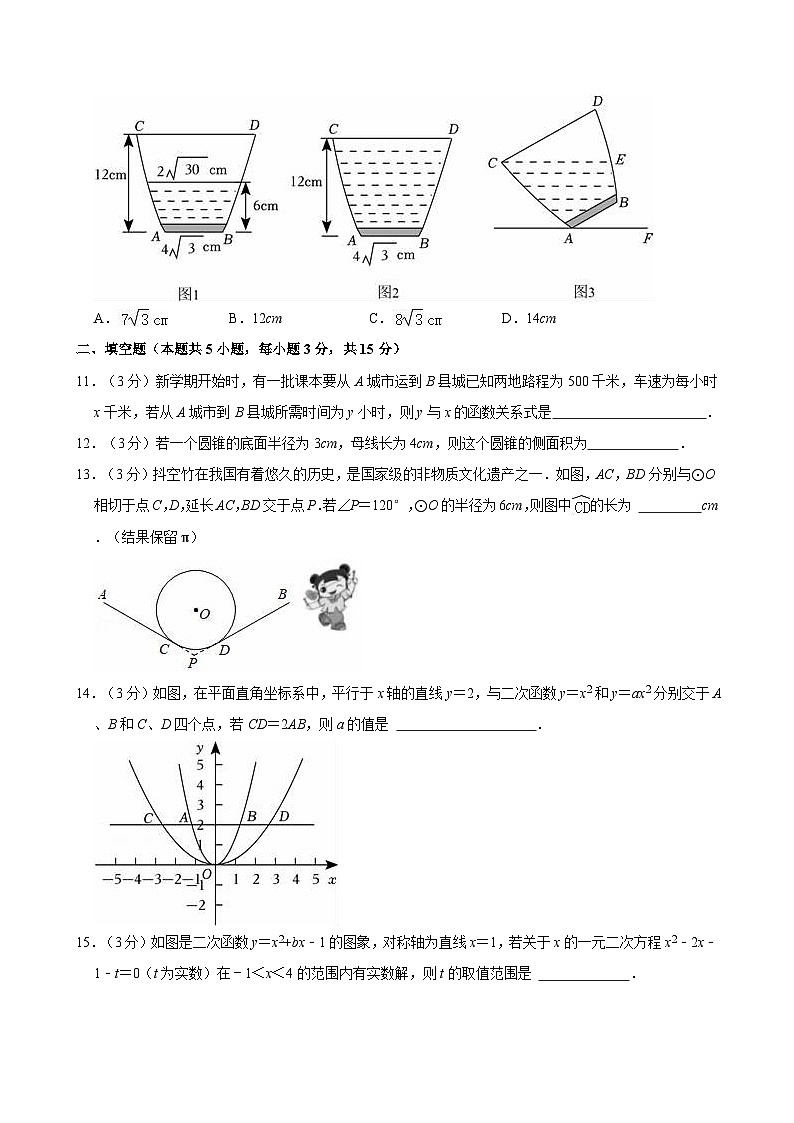
10．（3分）一个水杯竖直放置时的纵向截面如图1所示，其左右轮廓线AC，BD都是同一条抛物线的一部分，AB，CD都与水面桌面平行，已知水杯底部AB宽为4cm，水杯高度为12cm，当水面高度为6cm时，水面宽度为2cm．如图2先把水杯盛满水，再将水杯绕A点倾斜倒出部分水，如图3，当倾斜角∠BAF＝30°时，杯中水面CE平行水平桌面AF．则此时水面CE的值是（ ）
A．B．12cmC．D．14cm
二、填空题（本题共5小题，每小题3分，共15分）
11．（3分）新学期开始时，有一批课本要从A城市运到B县城已知两地路程为500千米，车速为每小时x千米，若从A城市到B县城所需时间为y小时，则y与x的函数关系式是 ．
12．（3分）若一个圆锥的底面半径为3cm，母线长为4cm，则这个圆锥的侧面积为 ．
13．（3分）抖空竹在我国有着悠久的历史，是国家级的非物质文化遗产之一．如图，AC，BD分别与⊙O相切于点C，D，延长AC，BD交于点P．若∠P＝120°，⊙O的半径为6cm，则图中的长为 cm．（结果保留π）
14．（3分）如图，在平面直角坐标系中，平行于x轴的直线y＝2，与二次函数y＝x2和y＝ax2分别交于A、B和C、D四个点，若CD＝2AB，则a的值是 ．
15．（3分）如图是二次函数y＝x2+bx﹣1的图象，对称轴为直线x＝1，若关于x的一元二次方程x2﹣2x﹣1﹣t＝0（t为实数）在﹣1＜x＜4的范围内有实数解，则t的取值范围是 ．
三、解答题（本大题含8道小题，共75分）
16．（10分）如图，反比例函数（k为常数，且k≠0）与一次函数y＝x+1的图象相交于点A（2，m）、B两点．
（1）求m和k的值；
（2）求点B的坐标．
17．（8分）如图是抛物线y1＝ax2+bx+c（a≠0）图象的一部分，抛物线的顶点为A，与x轴的一个交点为B，直线y2＝kx+b（k≠0）与抛物线交于A，B两点．
（1）写出不等式kx+b＞ax2+bx+c中x的取值范围；
（2）若方程ax2+bx+c＝m有两个不相等的实数根，求m的取值范围．
18．（8分）如图，在△ABC中，AB＝AC，O是底边BC的中点，⊙O与腰AB相切于点D，求证：AC与⊙O相切．
19．（8分）如图，在平面直角坐标系中，四边形ABCD是矩形，BC∥x轴，AB＝1，，AD＝2．
（1）直接写出B、C、D三点的坐标；
（2）将矩形ABCD向右平移m个单位，使点A、C恰好同时落在反比例函数的图象上，得矩形A'B'C'D'，求矩形ABCD的平移距离m和反比例函数的解析式．
20．（8分）如图1，AB为⊙O直径，CB与⊙O相切于点B，D为⊙O上一点，连接AD、OC，若AD∥OC．
（1）求证：CD为⊙O的切线；
（2）如图2，过点A作AE⊥AB交CD延长线于点E，连接BD交OC于点F，若AB＝3AE＝12，求BF的长．
21．（8分）问题：如何设计击球路线？情境：某校羽毛球社团的同学们经常运用数学知识对羽毛球技术进行分析，下面是他们对击球线路的分析．如图，在平面直角坐标系中，点A在x轴上，球网AB与y轴的水平距离OA＝3m，击球点P在y轴上．
击球方案：
探究：
（1）求扣球和吊球时，求羽毛球飞行满足的函数表达式；
（2）①若选择扣球的方式，刚好能使球过网，求球网AB的高度为多少；
②若选择吊球的方式，求羽毛球落地点到球网的距离；
（3）通过对本次训练进行分析，若高远球的击球位置P保持不变，接球人站在离球网4m处，他可前后移动各1m，接球的高度为2.8m，要使得这类高远球刚好让接球人接到，请求出此类高远球抛物线解析式a的取值范围．
22．（12分）【背景素材】
预防传染病，某校定期对教室进行“药熏消毒”．已知药物释放阶段，室内每立方米空气中的含药量y（mg）与释放时间x（min）成一次函数；释放后，y与x成反比例如图所示，且2min时，室内每立方米空气中的含药量y（mg）达到最大值．
某兴趣小组记录部分y（mg）与x（min）的测量数据如表．满足的自变量x（min）的取值范围为有效消毒时间段．
【解决问题】
（1）求y关于x的函数表达式．
（2）求“药熏消毒”的有效消毒时间．
（3）若在实际生活中有效消毒时间段要求满足m≤x≤3m，其中m为常数，请确定实际生活中有效消毒的时间段．
23．（13分）抛物线，直线l的解析式为y2＝（k﹣1）x+2m﹣k+2．
（1）若抛物线经过点（0，﹣3），求抛物线的顶点坐标；
（2）探究抛物线y1与直线l的交点情况并说明理由；
（3）若抛物线经过点（x0，﹣4），且对于任意实数x满足两个条件：
①不等式x2+（2m﹣1）x﹣2m≥﹣4都成立；
②当k﹣2≤x≤k时，抛物线的最小值为2k+1．求直线l的解析式．
2024-2025学年辽宁省大连市沙河口区九年级（上）期中数学试卷
参考答案与试题解析
一、选择题（本题共10小题，每小题3分，共30分。）
1．【解答】解：∵y＝﹣3（x﹣1）2+2，a＝﹣3＜0，
∴该函数的图象开口向下，故选项A不符合题意；
对称轴是直线x＝1，故选项B不符合题意；
当x＝1时取得最大值2，故选项C不符合题意；
顶点坐标为（1，2），故选项D符合题意；
故选：D．
2．【解答】解：将点（﹣1，4）代入y＝，
∴k＝﹣4，
∴y＝，
∴点（4，﹣1）在函数图象上，
故选：A．
3．【解答】解：∵点P到圆心的距离2，大于圆的半径，
∴点P在圆外．
故选：C．
4．【解答】解：将抛物线y＝﹣x2向右平移2个单位，再向上平移2个单位，则所得的抛物线的函数表达式为y＝﹣（x﹣2）2+2．
故选：C．
5．【解答】解：由点（1，﹣3）的坐标满足反比例函数y＝﹣，故A是正确的；
由k＝﹣3＜0，双曲线位于二、四象限，故B也是正确的；
由反比例函数图象的对称性，可知反比例函数y＝﹣的图象关于y＝x对称是正确的，故C也是正确的，
由反比例函数的性质，k＜0，在每个象限内，y随x的增大而增大，不在同一象限，不具有此性质，故D是不正确的，
故选：D．
6．【解答】解：∵A、B、C、D是⊙O上的四点，OA⊥BC，
∴弧AC＝弧AB （垂径定理），
∴∠ADC＝∠AOB（等弧所对的圆周角是圆心角的一半）；
又∠AOB＝55°，
∴∠ADC＝27.5°．
故选：D．
7．【解答】解：y＝ax2﹣2ax﹣a+1＝a（x﹣1）2﹣2a+1，
∵抛物线顶点在x轴上，
∴﹣2a+1＝0，
解得a＝．
故选：B．
8．【解答】解：∵OA＝OD＝5cm，CD＝2cm，
∴OC＝OD﹣CD＝5﹣2＝3（cm），
∵OD⊥AB，
∴AC＝CB＝＝＝4（cm），
∴AB＝2AC＝8（cm）．
故选：C．
9．【解答】解：∵左侧每个钩码的质量均为2kg，杠杆总长30cm，
∴xy＝5×2×3＝30，
∴y＝（0＜x＜15），
故y与x的函数图象可能是C选项，
故选：C．
10．【解答】解：如图，以AB的中点为原点，直线AB为x轴，线段AB的中垂线为y轴，建立平面直角坐标系，
由题意得：A（﹣2，0），B（2，0），E（﹣，6），F（，6），
设抛物线的解析式为：y＝ax2+b，
将B（2，0），F（，6）代入，
得，
解得，
∴y＝x2﹣4，
当y＝12时，12＝x2﹣4，
解得x1＝4，x2＝﹣4，
∴C（﹣4，12），D（4，12），
根据题意可知，∠DCE＝∠BAF＝30°，设BE与y轴的交点坐标P，CD与y轴交于点Q，
在Rt△CPQ中，
CQ＝4，∠PCQ＝30°，
∴PQ＝4cm，
∴PO＝8cm，
∴P（0，8），
∴直线CE的解析式为：y＝kx+m，
将C（﹣4，12），P（0，8），代入，
得，
解得，
∴直线CE的解析式为：y＝x+8，
令x2﹣4＝x+8，
解得x＝或x＝，
∴点E的横坐标为，
当x＝时，y＝×+8＝5，
∴E（，5）．
∴CE＝＝14（cm），
故选：D．
二、填空题（本题共5小题，每小题3分，共15分）
11．【解答】解：由路程等于速度乘以时间得：xy＝500
∴y＝（x＞0）
故答案为：y＝（x＞0）．
12．【解答】解：圆锥的侧面积＝2π×3×4÷2＝12πcm2．
故答案为：12πcm2．
13．【解答】解：如图所示，连接OC，OD，
∵AC，BD分别与⊙O相切于点C，D，
∴∠OCP＝∠ODP＝90°，
由四边形内角和为360°可得，
∠COD＝360°﹣∠OCP﹣∠ODP﹣∠CPD
＝360°﹣90°﹣90°﹣120°
＝60°．
∴的长＝＝2π．
故答案为：2π．
14．【解答】解：把y＝2代入y＝x2中得，x2＝2，
∴
∴A的横坐标为，B横坐标为
∴
把y＝2代入y＝ax2得，ax2＝2，
∴
∴C的横坐标为，D横坐标为
∴
∵CD＝2AB，
∴
∴
故答案为：．
15．【解答】解：抛物线的对称轴为直线x＝﹣＝1，解得b＝﹣2，
∴抛物线解析式为y＝x2﹣2x﹣1，则顶点坐标为（1，﹣2），
当x＝﹣1时，y＝x2﹣2x﹣1＝2；当x＝4时，y＝x2﹣2x﹣1＝7，
当﹣1＜x＜4时，﹣2≤y＜7，
而关于x的一元二次方程x2﹣2x﹣1﹣t＝0（t为实数）在﹣1＜x＜4的范围内有实数解可看作二次函数y＝x2﹣2x﹣1与直线y＝t有交点，
∴﹣2≤t＜7．
故答案为：﹣2≤t＜7．
三、解答题（本大题含8道小题，共75分）
16．【解答】解：（1）将点A（2，m）坐标代入一次函数y＝x+1得：
m＝2+1＝3，
∴A（2，3），
∵点A（2，3）在反比例函数的图象上，
∴k＝2×3＝6．
∴m＝3，k＝6；
（2）由（1）可知，反比例函数解析式为y＝，联立方程组得：
，解得或，
∴B（﹣3，﹣2）．
17．【解答】解：（1）由图象可得，y2＞y1时，x＜1或x＞4，
∴不等式kx+b＞ax2+bx+c中x的取值范围为x＜1或x＞4．
（2）∵抛物线的顶点为A（1，3），
设y1＝a（x﹣1）2+3（a≠0），
将（4，0）代入y1＝a（x﹣1）2+3，
得9a+3＝0，
解得a＝﹣，
∴抛物线的解析式为y1＝﹣（x﹣1）2+3＝﹣x2+x+，
∴方程﹣x2+x+＝m有两个不相等的实数根，
即方程﹣x2+x+﹣m＝0有两个不相等的实数根，
∴Δ＝（）2﹣4×（﹣）×（﹣m）＝4﹣m＞0，
解得m＜3，
∴m的取值范围为m＜3．
18．【解答】证明：连接OA、OD，过点O作OE⊥AC于E，
∵AB＝AC，O是底边BC的中点，
∴∠BAO＝∠CAO，
∵⊙O与AB相切于点D，
∴OD⊥AB，
∵∠BAO＝∠CAO，OD⊥AB，OE⊥AC，
∴OE＝OD，
∵OD为⊙O的半径，
∴AC与⊙O相切．
19．【解答】解：（1）∵四边形ABCD是矩形，
∴AB＝CD＝1，AD＝BC＝2．
又∵点A的坐标为（），AD∥x轴，
∴B（），C（），D（）．
（2）由平移可知，
点A′的坐标为（﹣3+m，），点C′的坐标为诶（﹣1+m，）．
∵点A′和点C′都在反比例函数的图象上，
∴＝，
解得m＝4，
即矩形ABCD的平移距离是4，
则A′的坐标为（1，），
∴k＝1×，
∴反比例函数的解析式为y＝．
20．【解答】（1）证明：连接OD，
∵CB与⊙O相切于点B，
∴OB⊥BC，
∵AD∥OC，
∴∠A＝∠COB，∠ADO＝∠DOC，
∵OA＝OD，
∴∠A＝∠ADO＝∠COB＝∠DOC，
∴△DOC≌△BOC（SAS），
∴∠ODC＝∠OBC＝90°，
∴OD⊥DC，
又OD为⊙O半径，
∴CD为⊙O的切线；
（2）解：设CB＝x，
∵AE⊥EB，
∴AE为⊙O的切线，
∵CD、CB为⊙O的切线，
∴ED＝AE＝4，CD＝CB＝x，∠DOC＝∠BCO，
∴BD⊥OC，
过点E作EM⊥BC于M，则EM＝12，CM＝x﹣4，
∴（4+x）2＝122+（x﹣4）2，
解得x＝9，
∴CB＝9，
∴OC＝＝，
∵＝，
∴BF＝．
21．【解答】解：（1）∵y＝﹣0.4x+b，直线经过点（1，2.4），
∴﹣0.4+b＝2.4．
解得：b＝2.8．
∴扣球时，羽毛球飞行满足的函数表达式为：y＝﹣0.4x+2.8．
∴点P的坐标为（0，2.8）．
吊球时，设y＝a（x﹣1）2+3.2．
∵抛物线经过点（0，2.8），
∴2.8＝a（0﹣1）2+3.2．
解得：a＝﹣0.4．
∴吊球时，羽毛球飞行满足的函数表达式为：y＝﹣0.4（x﹣1）2+3.2．
（2）①当x＝3时，y＝﹣0.4×3+2.8＝1.6．
答：球网AB的高度为1.6米．
②当y＝0时，0＝﹣0.4（x﹣1）2+3.2．
解得：x1＝1+2，x2＝1﹣2（不合题意，舍去）．
∴羽毛球落地点到球网的距离为1+2﹣3＝（2﹣2）米．
（3）①接球点为（6，2.8）．
若最大高度为5.8，那么a的值最小．
∵点P的坐标为（0，2.8），
∴n＝3．
∴y＝a（x﹣3）2+5.8．
∴2.8＝a（6﹣3）2+5.8．
解得：a＝﹣．
②接球点为（8，2.8）．
若最大高度为4.8，那么a的值最大．
∵点P的坐标为（0，2.8），
∴n＝4．
∴y＝a（x﹣4）2+4.8．
∴2.8＝a（8﹣4）2+4.8．
解得：a＝﹣．
∴a的取值范围为：﹣≤a≤﹣．
22．【解答】解：（1）由题意，观察图象AB过点（0.5，2.5），（1，3），
设AB解析式为y＝mx+n，
∴，
∴，
∴AB解析式为y＝x+2．
设BC所在反比例函数为y＝，
又过点（2.5，3.2），
∴k＝2.5×3.2＝8．
∴BC所在反比例函数为y＝；
（2）∵AB为y＝x+2，
又令y＝，
∴x＝，
又AB所在函数y随x的增大而增大，
∴x≥，
∵BC所在反比例函数为y＝，
令y＝，
∴x＝3．
又BC所在反比例函数y随x的增大而减小，
∴x≤3，
∴有效消毒时间段为≤x≤3．
（3）由题意，m≤2≤3m时，（即≤m≤2），
①把x＝m，y＝代入y＝x+2，得＝m+2，
解得m＝，
把x＝3m＝2代入y＝，得y＝4，满足题意．
∴≤x≤2，
②把x＝3m，y＝代入y＝，得＝，
解得a＝1．
把x＝a＝1代入y＝x+2，解得y＝3，满足题意．
∴1≤x≤3．
综上，≤x≤2或1≤x≤3．
23．【解答】解：（1）抛物线与y轴交点的纵坐标为﹣3，即：﹣2m＝﹣3，解得：m＝，
则抛物线表达式为：y＝x2+2x﹣3＝（ x+1）2﹣4，
则抛物线的顶点（﹣1，﹣4）；
（2）抛物线：y＝x2+（2m﹣1）x﹣2m，
直线：y＝（k﹣1）x+2m﹣k+2，
则x2+（2m﹣k）x﹣4m+k﹣2＝0，
则Δ＝（2m﹣k）2﹣4（﹣4m+k﹣2）＝（2m﹣k）2+16m﹣4k+8，
＝（2m﹣k）2+4（2m﹣k）+8m+4+4，
＝（2m﹣k+2）2+8m+4，
∵m＞﹣，
∴（2m﹣k+2）2+8m+4＞0
∴Δ＞0，抛物线与直线l必有两个交点．
（3）依题意可知y最小值＝﹣4，
即： [4×1×（﹣2m）﹣（2m﹣1）2]＝﹣4，
解得：m＝或﹣，
∵﹣＜m，
∴m＝，此时抛物线的对称轴为直线 x＝﹣1，
①当k≤﹣1时，抛物线在k﹣2≤x≤k上，图象下降，y随x增大而减小．此时y最小值＝k2+2k﹣3，
∴k2+2k﹣3＝2k+1，
解得：k1＝2＞﹣1（舍去），k2＝﹣2，
②当k﹣2＜﹣1＜k，即﹣1＜k＜1时，抛物线在k﹣2≤x≤k上，y最小值＝﹣4，
∴2k+1＝﹣4，
∴解得：k＝﹣＜﹣1 （舍去）•
③当k﹣2≥﹣1，即k≥1时，抛物线在k﹣2≤x≤k上，图象上升，y随x增大而增大，
此时y最小值＝（k﹣2）2+2 （k﹣2）﹣3，
即（k﹣2）2+2 （k﹣2）﹣3＝2k+1，
解得：k1＝2+2，k2＝2﹣2＜1 （舍去），
综上所述，直线l：y＝﹣3 x+7或y＝（1+2）x+3﹣2．
扣球
羽毛球的飞行高度y（m）与水平距离x（m）近似满足一次函数关系C1：y＝﹣0.4x+b，当羽毛球的水平距离为1m时，飞行高度为2.4m．
吊球
羽毛球的飞行高度y（m）与水平距离x（m）近似满足二次函数关系C2，此时当羽毛球飞行的水平距离是1米时，达到最大高度3.2米．
高远球
羽毛球的飞行高度y（m）与水平距离x（m）近似满足二次函数关系C3：y＝a（x﹣n）2+h，且飞行的最大高度在4.8m和5.8m之间．
x
…
0.5
1
1.5
2
2.5
3
…
y
…
2.5
3
3.5
4
3.2
2.
…