湖北省十堰市2024-2025学年九年级上学期11月月考数学试题

这是一份湖北省十堰市2024-2025学年九年级上学期11月月考数学试题，文件包含数学docx、数学pdf等2份试卷配套教学资源，其中试卷共8页， 欢迎下载使用。

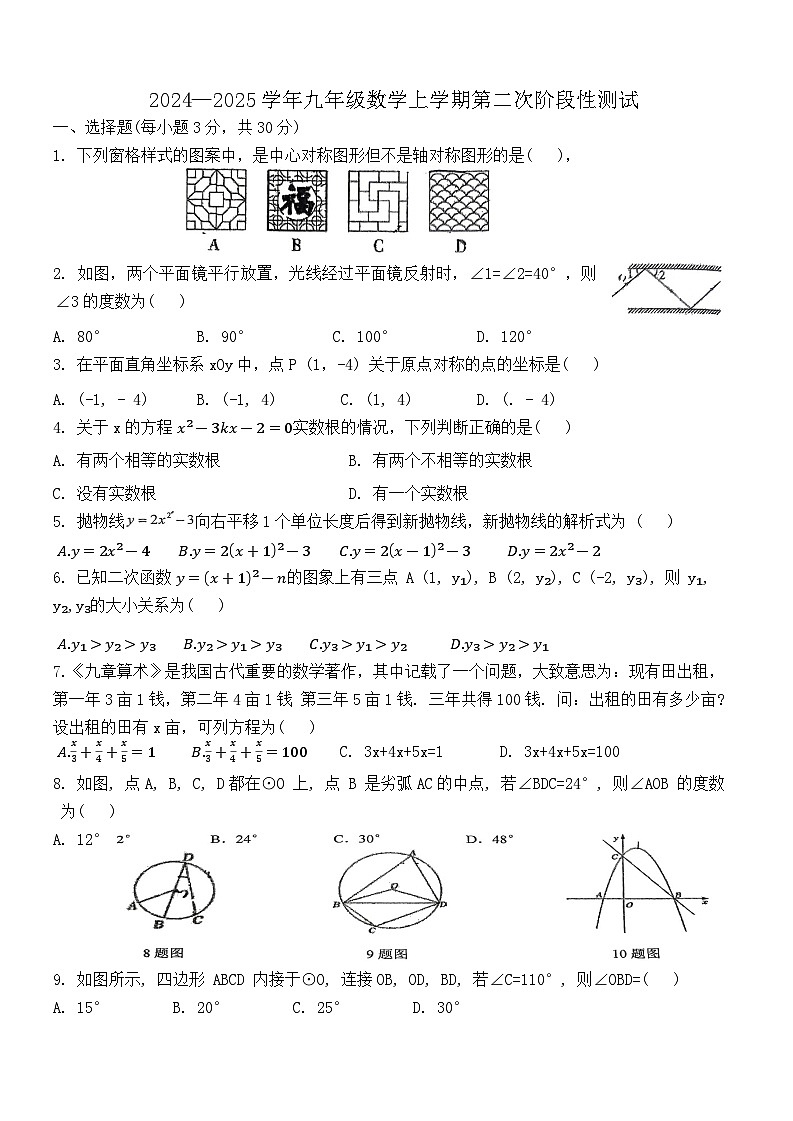
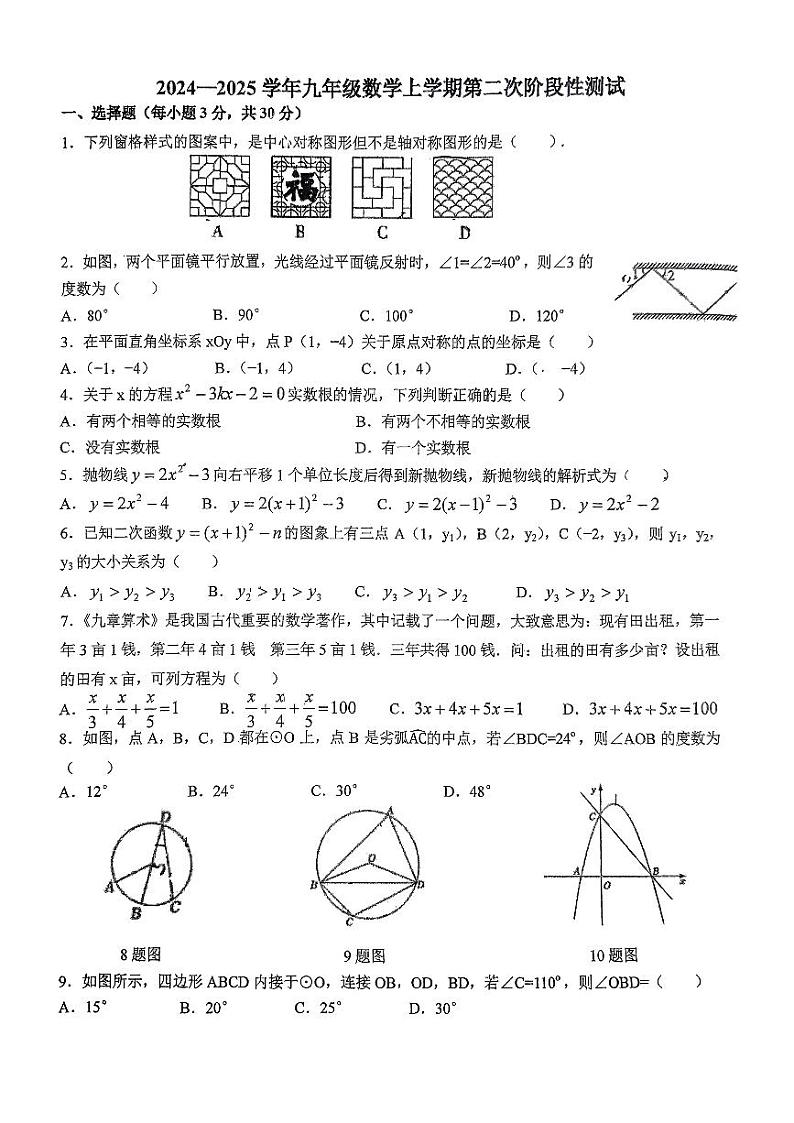
1. 下列窗格样式的图案中，是中心对称图形但不是轴对称图形的是( )，
2. 如图，两个平面镜平行放置，光线经过平面镜反射时，∠1=∠2=40°，则∠3的度数为( )
A. 80° B. 90° C. 100° D. 120°
3. 在平面直角坐标系xOy中，点P (1，-4) 关于原点对称的点的坐标是( )
A. (-1, - 4) B. (-1, 4) C. (1, 4) D. (. - 4)
4. 关于x的方程 x²-3kx-2=0实数根的情况，下列判断正确的是( )
A. 有两个相等的实数根 B. 有两个不相等的实数根
C. 没有实数根 D. 有一个实数根
5. 抛物线向右平移1个单位长度后得到新抛物线，新抛物线的解析式为 ( )
A.y=2x²-4 B.y=2x+1²-3 C.y=2x-1²-3 D.y=2x²-2
6. 已知二次函数 y=x+1²-n的图象上有三点 A (1, y₁), B (2, y₂), C (-2, y₃), 则 y₁, y₂,y₃的大小关系为( )
A.y₁>y₂>y₃ B.y₂>y₁>y₃ C.y₃>y₁>y₂ D.y₃>y₂>y₁
7.《九章算术》是我国古代重要的数学著作，其中记载了一个问题，大致意思为：现有田出租，第一年3亩1钱，第二年4亩1钱 第三年5亩1钱. 三年共得100钱. 问：出租的田有多少亩? 设出租的田有x亩，可列方程为( )
A.x3+x4+x5=1 B.x3+x4+x5=100 C. 3x+4x+5x=1 D. 3x+4x+5x=100
8. 如图, 点A, B, C, D都在⊙O 上, 点 B 是劣弧AC的中点, 若∠BDC=24°, 则∠AOB 的度数为( )
A. 12°
9. 如图所示, 四边形 ABCD 内接于⊙O, 连接OB, OD, BD, 若∠C=110°, 则∠OBD=( )
A. 15° B. 20° C. 25° D. 30°10. 如图, 抛物线 y=ax²+bx+c与x轴交于A(-1,0), B(3,0)两点, 与y轴交于点C, 直线y= kx+m经过点 C, B. 有以下结论: ①抛物线的对称轴是 x=1; ②a-b+c=0; ⑬-10;④若 a=-1, 则k=-1. 其中正确的结论有 ( )
A. 1个 B. 2个 C. 3个 D. 4个
二、填空题(每小题3分，共15分)
11. 已知关于x的一元二次方程( m-2x²+4x-3=0有实数根，则m的取值范围为 .
12.飞机着陆后滑行的距离S(m)与滑行的时间t(s)之间的关系式为 S=60t-1.5t²,则飞机滑行 s停下.
13. 在直径为650cm的圆柱形油槽内装入一些油以后，截面如图，若油面的宽AB=600cm，则油的最大深度为 cm.
14.如图，将正方形AOBC绕点O逆时针旋转30°后得到正方形 DOEF，则点D 的坐标为 .
15. 如图, 正方形ABCD中, AB=2, 把△ABC绕点A逆时针旋转60°得到△AEF, 连接DF.则(1)∠CAE= ; (2)DF= .
三、解答题(75分)
16. (1)(3分) 计算: 20×|-13|+4-3-1 (2)(3分) 解方程: 2x²+5x-3=0
17.(6分)某小区在绿化工程中有一块长为20m、宽为8m的矩形空地，计划在其中修建两块相同的矩形绿地，使它们的面积之和为56m²，两块绿地之间及周边留有宽度相等的人行通道(如图所示)，求人行通道的宽度.
18. (6分)已知二次函数 y=ax²-2ax+3(a为常数, a≠0).
(1) 若a<0，求证：该函数的图象与x轴有两个公共点；
(2) 若函数经过 (-1, 0), 求a的值, 并求当-119.(8分) 如图, 在 Rt△ABC 中, ∠ACB=90°, ∠B=30°, 将△ABC绕点C 按顺时针方向旋转n度后，得到△DEC，点D 刚好落在AB边上.
(1) 求n的值;
(2) 若F是DE的中点，判断四边形ACFD 的形状，并说明理由.20.(8分)如图, 在△ABC中, AB=AC,以AC为直径的⊙O交AB于点D, 交BC于点E.
(1) 求证: BE=CE;
(2) 若BD=2, BE=3, 求AC 的长.
21.(9分)某超市购入一批进价为10元/盒的糖果进行销售，经市场调查发现：销售单价不低于进价时，日销售量y(盒) 与销售单价x(元) 是一次函数关系，下表是y与x的几组对应值.
(1) 求y与x的函数表达式；
(2) 糖果销售单价定为多少元时，所获日销售利润最大，最大利润是多少?
(3) 若超市决定每销售一盒糖果向儿童福利院赠送一件价值为 m元的礼品，赠送礼品后，为确保该种糖果日销售获得的最大利润为392元，求m的值.
22.(10分) 利用素材解决：《桥梁的设计》
销售单价x/元

12
14
16
18
20

销售量 y/盒

✔
52
48
44
40

问题驱动
某地欲修建一座拱桥，桥的底部两端间的水面宽AB=L， 称跨度， 桥面最高点到AB的距离 CD=h称拱高， 拱桥的轮廓可以设计成是圆弧型或抛物线型， 若修建拱桥的跨度L=32米, 拱高h=8米.
设计方案
方案一
方案二
设计类型
圆弧形
抛物线形
任务一
设计成圆弧型， 求该圆弧所在圆的半径.
设计成抛物线型，以AB所在直线为x轴，AB 的垂直平分线为 y 轴建立坐标系， 求桥拱的函数表达式.
任务二
如图， 一艘货船露出水面部分的横截面为矩形EFGH， 测得EF=6.1 米， EH=16米. 请你通过计算说明货船能否顺利通过圆弧形桥梁.
23.(10分)在Rt△ABC中,∠C=90°,将△ABC绕点A 顺时针旋转得到△ADE,旋转角小于∠CAB,点B 的对应点为点D, 点C的对应点为点E, DE交AB 于点O, 延长DE交BC于点P.
(1) 如图1, 求证: PC=PE;
(2)当AD∥BC时,
①如图2, 若CA=6, CB=8, 求线段BP 的长;
②如图3, 连接BD, CE, 延长CE交BD于点F, 判断F是否为线段BD的中点, 并说明理由.
24.(12分) 如图, 抛物线 y=ax²+bx+c分别交 x轴于点 A, B, 交 y轴于点 C(0, - 3), 顶点为D(1, - 4).
(1)求该二次函数的解析式；
(2)如图①, 点E是x轴上一动点, 连接CD, CE, DE, 是否存在一点E, 使得△CDE 的周长最小,若存在，请求出点E的坐标及此时△CDE的周长，若不存在，请说明理由；
(3)如图②，点Q是x轴上方抛物线上的一个动点，连接CQ，若直线CQ将四边形CBQA 的面积分为1：3的两部分，求直线CQ 的解析式.