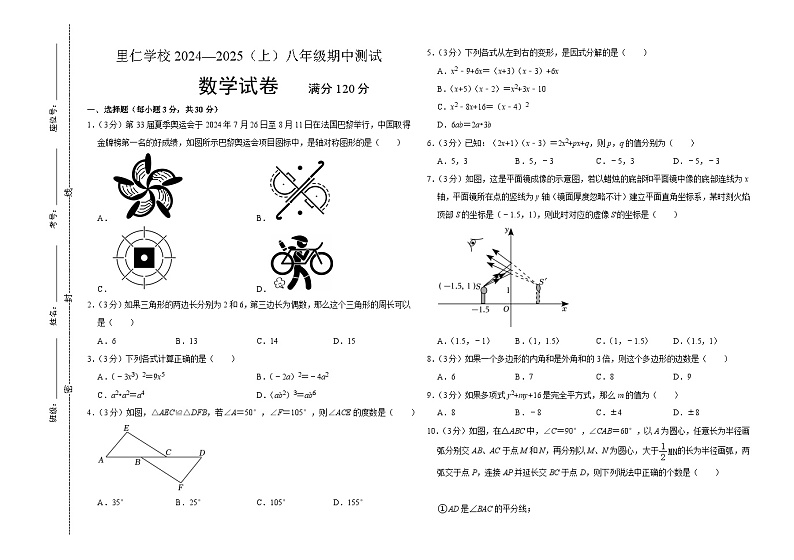
辽宁省灯塔市五里镇里仁中学2024-2025学年八年级上学期期中数学试卷

这是一份辽宁省灯塔市五里镇里仁中学2024-2025学年八年级上学期期中数学试卷，文件包含辽宁省灯塔市五里镇里仁中学2024-2025学年八年级上学期期中数学试卷docx、评分标准docx等2份试卷配套教学资源，其中试卷共12页， 欢迎下载使用。
1．（3分）第33届夏季奥运会于2024年7月26日至8月11日在法国巴黎举行，中国取得金牌榜第一名的好成绩，如图所示巴黎奥运会项目图标中，是轴对称图形的是（ ）
A．B．
C．D．
2．（3分）如果三角形的两边长分别为2和6，第三边长为偶数，那么这个三角形的周长可以是（ ）
A．6B．13C．14D．15
3．（3分）下列各式计算正确的是（ ）
A．（﹣3x3）2＝9x5B．（﹣2a）2＝﹣4a2
C．a2•a2＝a4D．（ab2）3＝ab6
4．（3分）如图，△AEC≌△DFB，若∠A＝50°，∠F＝105°，则∠ACE的度数是（ ）
A．35°B．25°C．105°D．155°
5．（3分）下列各式从左到右的变形，是因式分解的是（ ）
A．x2﹣9+6x＝（x+3）（x﹣3）+6x
B．（x+5）（x﹣2）＝x2+3x﹣10
C．x2﹣8x+16＝（x﹣4）2
D．6ab＝2a•3b
6．（3分）已知：（2x+1）（x﹣3）＝2x2+px+q，则p，q的值分别为（ ）
A．5，3B．5，﹣3C．﹣5，3D．﹣5，﹣3
7．（3分）如图，这是平面镜成像的示意图，若以蜡烛的底部和平面镜中像的底部连线为x轴，平面镜所在点的竖线为y轴（镜面厚度忽略不计）建立平面直角坐标系，某时刻火焰顶部S的坐标是（﹣1.5，1），则此时对应的虚像S'的坐标是（ ）
A．（1.5，﹣1）B．（1，1.5）C．（1，﹣1.5）D．（1.5，1）
8．（3分）如果一个多边形的内角和是外角和的3倍，则这个多边形的边数是（ ）
A．6B．7C．8D．9
9．（3分）如果多项式y2+my+16是完全平方式，那么m的值为（ ）
A．8B．﹣8C．±4D．±8
10．（3分）如图，在△ABC中，∠C＝90°，∠CAB＝60°，以A为圆心，任意长为半径画弧分别交AB、AC于点M和N，再分别以M、N为圆心，大于的长为半径画弧，两弧交于点P，连接AP并延长交BC于点D，则下列说法中正确的个数是（ ）
①AD是∠BAC的平分线；
②∠ADB＝120°；
③点D在AB的垂直平分线上；
④S△DAC：S△ABC＝1：3．
A．1B．2C．3D．4
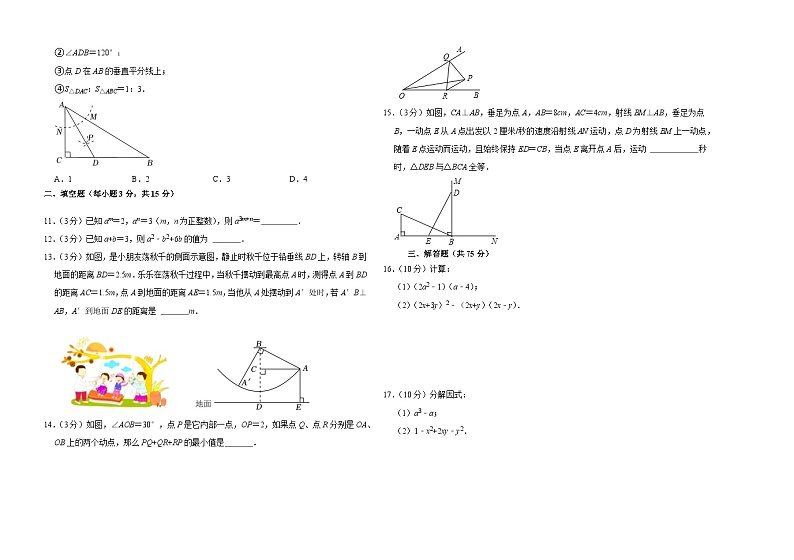
填空题（每小题3分，共15分）
11．（3分）已知am＝2，an＝3（m，n为正整数），则a3m+n＝ ．
12．（3分）已知a+b＝3，则a2﹣b2+6b的值为 ．
13．（3分）如图，是小朋友荡秋千的侧面示意图，静止时秋千位于铅垂线BD上，转轴B到地面的距离BD＝2.5m．乐乐在荡秋千过程中，当秋千摆动到最高点A时，测得点A到BD的距离AC＝1.5m，点A到地面的距离AE＝1.5m，当他从A处摆动到A′处时，若A′B⊥AB，A′到地面DE的距离是 m．
14．（3分）如图，∠AOB＝30°，点P是它内部一点，OP＝2，如果点Q、点R分别是OA、OB上的两个动点，那么PQ+QR+RP的最小值是 ．
15．（3分）如图，CA⊥AB，垂足为点A，AB＝8cm，AC＝4cm，射线BM⊥AB，垂足为点B，一动点E从A点出发以2厘米/秒的速度沿射线AN运动，点D为射线BM上一动点，随着E点运动而运动，且始终保持ED＝CB，当点E离开点A后，运动 秒时，△DEB与△BCA全等．
三、解答题（共75分）
16．（10分）计算：
（1）（2a2﹣1）（a﹣4）；
（2）（2x+3y）2﹣（2x+y）（2x﹣y）．
17．（10分）分解因式：
（1）a3﹣a；
（2）1﹣x2+2xy﹣y2．
18．（8分）某中学图书馆的通道闸机如图①所示，当它的双翼展开时，示意图如图②所示，双翼边缘的端点A与D之间的距离为10cm，双翼的边缘AC＝DF＝54cm，且与闸机箱的夹角∠ACB＝∠DFE＝30°，求当双翼收起时，可以通过闸机的物体的最大宽度．
19．（8分）如图，△ABC三个顶点的坐标分别为A（1，1），B（4，2），C（3，4）．
（1）请写出△ABC关于x轴对称的△A1B1C1的各顶点坐标；
（2）请画出△ABC关于y轴对称的△A2B2C2；
（3）在x轴上求作一点P，使点P到A、B两点的距离和最小，请标出P点，并直接写出点P的坐标 ．
20．（10分）在Rt△ABC中，∠ACB＝90°，AC＝BC，D为BC中点，CE⊥AD于E，BF∥AC交CE的延长线于F．
（1）求证：△ACD≌△CBF；
（2）求证：AB垂直平分DF．
21．（10分）如图1，点C是BE上一点，以BC，CE为边在BE同侧作等边△ABC和等边△EDC，连接BD与AE．
（1）求证：DB＝AE；
（2）如图2，若点F和点G分别为BD，AE的中点，连接CF，CG，FG，判断△CFG的形状，并说明理由．
22．（12分）【探究】如图①，从边长为a的大正方形中剪掉一个边长为b的小正方形，将阴影部分沿虚线剪开，拼成图②的长方形．
（1）请你分别表示出这两个图形中阴影部分的面积：图① 图② ；
（2）比较两图的阴影部分面积，可以得到乘法公式： （用字母a、b表示）；
【应用】请应用这个公式完成下列各题：
①已知2m﹣n＝3，2m+n＝4，则4m2﹣n2的值为 ；
②计算：（x﹣3）（x+3）（x2+9）；
【拓展】计算（2+1）（22+1）（24+1）（28+1）…（232+1）的结果为 ．
23．（14分）综合实践
问题情境：数学活动课上，王老师出示了一个问题：
如图1，在△ABC中，AB＝AC，点D是BC边上一点，连接AD，BE平分∠ABC交AD于点E，点F是AC上一点，连接FE并延长交BC于点G，∠AEF＝∠ABD，求证：∠BAD＝∠CGF．
（1）独立思考：求证：∠BAD＝∠CGF．
（2）实践探究：在同学们独立完成后，王老师又提出了新问题，求证DG＝AF，王老师的问题引发了同学们的思考，各小组进行了积极的讨论，仍不得其解．王老师给出提示：“数学中常通过把一个问题特殊化来找到解题思路．”“善思小组”的同学茅塞顿开，在对上述问题进行特殊化研究之后发现，如图2，当AB＝BD时，很容易发现AE＝DE，请你完成图2特殊情况下的证明DG＝AF．
（3）问题解决：相信你从上面也得到了启发，参将“善思小组”的思路，请你在图1中完成王老师的问题，证明DG＝AF．