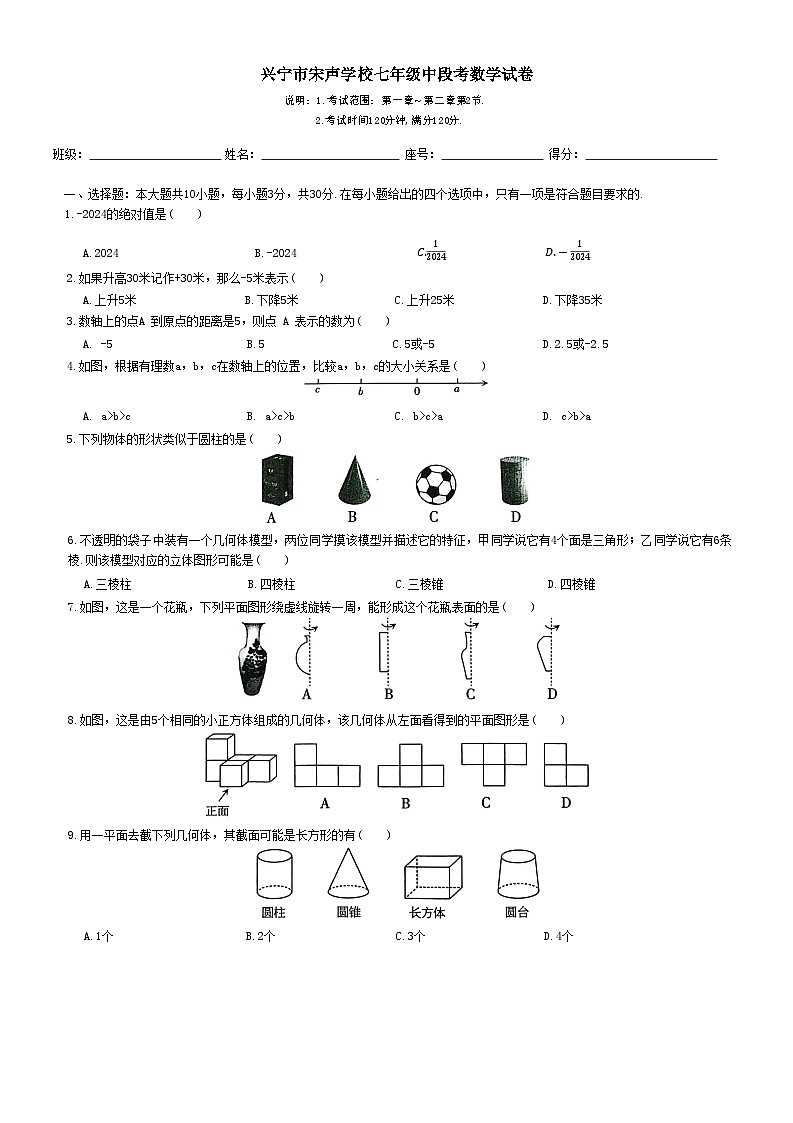
广东省梅州市兴宁市宋声学校2024-2025学年七年级上学期11月期中考试数学试题

这是一份广东省梅州市兴宁市宋声学校2024-2025学年七年级上学期11月期中考试数学试题，共9页。试卷主要包含了考试范围，下列物体的形状类似于圆柱的是等内容，欢迎下载使用。

2.考试时间120分钟,满分120分.
班级： 姓名： 座号： 得分：
一、选择题：本大题共10小题，每小题3分，共30分.在每小题给出的四个选项中，只有一项是符合题目要求的.
1.-2024的绝对值是( )
A.2024 B.-2024 C.12024 D.-12024
2.如果升高30米记作+30米，那么-5米表示( )
A.上升5米 B.下降5米 C.上升25米 D.下降35米
3.数轴上的点A 到原点的距离是5，则点 A 表示的数为( )
A. -5 B.5 C.5或-5 D.2.5或-2.5
4.如图，根据有理数a，b，c在数轴上的位置，比较a，b，c的大小关系是( )
A. a>b>c B. a>c>b C. b>c>a D. c>b>a
5.下列物体的形状类似于圆柱的是( )
6.不透明的袋子中装有一个几何体模型，两位同学摸该模型并描述它的特征，甲同学说它有4个面是三角形；乙同学说它有6条棱.则该模型对应的立体图形可能是( )
A.三棱柱 B.四棱柱 C.三棱锥 D.四棱锥
7.如图，这是一个花瓶，下列平面图形绕虚线旋转一周，能形成这个花瓶表面的是( )
8.如图，这是由5个相同的小正方体组成的几何体，该几何体从左面看得到的平面图形是( )
9.用一平面去截下列几何体，其截面可能是长方形的有( )
A.1个 B.2个 C.3个 D.4个
10.小刚同学设计了一种“幻圆”游戏,将-1,2,-3,4,-5,6,-7,8分别填入图中的圆圈内,使横、竖以及内外两圈上的4个数之和都相等，他已经将-1，4，6，-7，8这五个数填入了圆圈内，则图中a+b的值为( )
A. -6 B. -3 C.-4 D. -1
二、填空题：本大题共5小题，每小题3分，共15分.
11.国扇文化有深厚的文化底蕴，历来中国有“制扇王国”之称.打开折扇时，随着扇骨的移动形成一个扇面，这种现象可以用数学原理解释为 .
12.若一个棱柱有12个顶点，且所有侧棱长的和为30cm，则每条侧棱长为 cm.
13.绝对值小于4的所有整数的和是 .
14.已知点A、点B、点C是同一条数轴上的三个点，点A 在数轴上表示的数是1，AB=2，当点 B 在点A 右侧时，若A，B，C有一点是其构成的三条线段中其中一条线段的中点，则点 A，B，C 称为“和谐点”，此时点 C在数轴上表示的数是 .
15.在课题学习中，老师要求用长为12cm，宽为8cm 的长方形纸片制作一个无盖的长方体纸盒.三位同学分别以下列方式在长方形纸片上截去两角(图中阴影部分)，然后沿虚线折成一个无盖的长方体纸盒.
甲：如图1，盒子底面的四边形ABCD 是正方形.
乙：如图2，盒子底面的四边形 ABCD 是正方形.
丙：如图3，盒子底面的四边形ABCD是长方形，AB=2AD.
将三位同学折成的无盖的长方体的容积按从小到大的顺序排列为 .
三、解答题(一)：本大题共3小题，每小题7分，共21分.
16.请把图中的平面图形与其绕所画直线旋转一周之后形成的立体图形用线连接起来.
)
)
17.国庆节快到了，小明同学准备了一份礼物送给自己的好朋友.他设计了一个正方体盒子进行包装，如图所示，由于粗心少设计了其中一个顶盖，请你把它补上，使其成为一个两面均有盖的正方体盒子.任意画出一种成功的设计图(在图中补充)，并将-1，-2，-3，1，2，3这些数字分别填入六个小正方形，使得折成的正方体相对面上的两个数相加得0(直接在图中填上即可).
18.计算: 1-313+-12--13+112;
(2)(-5.3)+|-2.5|+(-3.2)-(+4.8).
四、解答题(二)：本大题共3小题，每小题9分，共27分.
19.如图，这是一个长为4cm，宽为3cm的长方形纸片，将该长方形纸片绕一条边所在的直线旋转一周，然后用平面沿与AB平行的方向去截所得的几何体，求截面的最大面积(结果保留π).
20.某仓库3天内粮食进、出库(“+”表示进库，“一”表示出库)的吨数如下：+4,-3,+22,-8,-2,+17.
(1)经过这3天，仓库里的粮食是增加了还是减少了? 增加或减少了多少吨?
(2)如果进、出库的装卸费都是每吨30元，那么这3天总共要付多少元的装卸费?
21.小明早晨跑步，他从自己家出发，向东跑了2km到达小彬家，继续向东跑了1.5k m到达小红家，然后又向西跑了4.5km到达学校，最后又向东跑回到自己家.
(1)①若以小明家为原点，向东的方向为正方向，用1个单位长度表示1km，请在如图所示的数轴上，分别用点A，B，C表示出小彬家、小红家和学校的位置.
②小彬家与学校之间的距离为 km.
(2)如果小明跑步的速度是200m/ min，那么小明跑步一共用了多长时间?
五、解答题(三)：本大题共2小题，第22题13分，第23题14分，共27分.
22.如图，这是由棱为1 cm的立方体小木块搭建成的几何体从3个方向看到的形状图.
(1)请你观察它是由 个立方体小木块组成的；
(2)在从上面看到的形状图中标出相应位置上立方体小木块的个数；
(3)求出该几何体的表面积(包含底面).
23.观察下列两个等式： 3+2=3×2-1,4+53=4×53-1. 给出定义如下：我们称使等式a+b= ab -1成立的一对有理数a,b为“共生有理数对”,记为(a,b).如:数对(3,2),(4, 53 )都是“共生有理数对”.
(1)数对((-2,1),(5, 32 )中是“共生有理数对”的是 .
(2)若(a,3)是“共生有理数对”,求a的值.
(3)若(m，n)是“共生有理数对”，则(-n，-m)是不是“共生有理数对”? 请说明理由.
参考答案与解析
1. A - 2024的绝对值是2024.
2. B 如果升高30米记作+30米,那么-5米表示下降5米.
3. C 根据题意知：到数轴原点的距离是5的点表示的数，即绝对值是5的数，应是±5.
4. A 由题意,得c5. D A.立体图形为长方体；B.立体图形为圆锥；C.立体图形为球.
6. C 侧面是三角形，说明它是棱锥，底面是三角形，说明它是三棱锥.
7. C 将选项所给的平面图形绕虚线旋转一周，可得C选项符合所给图形.
8. D从左面看，底层是两个小正方形，上层的左边是一个小正方形.
9. B 圆锥和圆台用平面去截不可能得到长方形.
10. B - 1+2-3+4-5+6-7+8=4,因为横、竖以及内外两圈上的4个数字之和都相等，所以两个圈的和是2,横、竖的和也是2,则-7-1+8+a=2,解得a=2,-7+6+b+8=2,解得b=-5,所以a+b=2+(-5)=-3.
11.线动成面 由题意知，这种现象可以用数学原理解释为线动成面.
12.5 一个棱柱有12个顶点，所以它是六棱柱，即有6条侧棱，又因为所有侧棱长的和是30cm，所以每条侧棱长是30÷6=5( cm).
13.0 绝对值小于4的所有整数是-3,-2,-1,0,1,2,3,其和为-3+(-2)+(-1)+0+1+2+3=0.
14.-1,2,5 ①当A为CB 中点时,因为AB=2,所以CA=AB=2，又因为点 A在数轴上表示的数是1,所以点C在数轴上表示的数为1-CA=1-2=-1;②当B为AC中点时,因为AB=2,所以BC=AB=2,又因为点A 在数轴上表示的数是1，所以点C在数轴上表示的数为1+AB+BC=1+2+2=5;③当C为AB 中点时,因为AB=2,所以AC=CB=AB÷2=2÷2=1，又因为点A在数轴上表示的数是1，所以点C在数轴上表示的数为1+AC=1+1=2.
15.乙<甲<丙 甲所折成的无盖长方体的容积为5×3×3=45(cm³)，乙所折成的无盖长方体的容积为10×2×2=40(cm³),丙所折成的无盖长方体的容积为6×4×2=48(cm³)，所以从小到大排列顺序为乙<甲<丙.
16.解：将图中的平面图形与其绕所画直线旋转一周之后形成的立体图形用线连接起来如图所示：(7分)
17.解：如图，答案不唯一.(7分)
18.解: 1-313+-12--13+112= -313+13+-12+112=-3+1=-2;(3分)
(2)(-5.3)+|-2.5|+(-3.2)-(+4.8)=-5.3+2.5-3.2-4.8=2.5-(5.3+3.2+4.8)=2.5-13.3=-10.8.(7分)
19.解：①若把长方形ABCD绕AB边所在的直线旋转一周，得到的几何体为圆柱，
圆柱的底面半径为4cm，高为3cm，
用平面沿与 AB平行的方向去截所得的几何体，截面是长方形，
所以截面的最大面积为4×2×3=24(cm²);(4分)
②若把长方形ABCD绕AD 边所在的直线旋转一周，得到的几何体为圆柱，
圆柱的底面半径为3cm，高为4cm，
用平面沿与 AB平行的方向去截所得的几何体，截面是圆，
所以截面的最大面积为 3²×π=9πcm².(8分)
因为9π>24,
所以截面的最大面积为9πcm².(9分)
20.解:(1)4+(-3)+22+(-8)+(-2)+17=30(吨).
答：仓库里的粮食增加了，增加了30吨.(4分)
(2)(1+4|+|-3|+|+22|+|-8|+|-2|+|+17|)×30=1680(元).
答：这3天总共要付装卸费1680元.(9分)
21.解:(1)①如图所示:(3分)
②3(5分)
提示：小彬家与学校之间的距离为2-(-1)=3( km).
(2)小明一共跑了2+1.5+4.5+1=9( km),
小明跑步一共用的时间为9000÷200=45( min).
答:小明跑步一共用了45 min.(9分)
22.解:(1)10(4分)
因为从上面看有6个正方形，所以最底层有6个正方体小木块，由从正面看和从左面看可得第二层有3个正方体小木块，第三层有1个正方体小木块，所以共由10个正方体小木块组成.
(2)如图所示:(8分)
(3)表面积为6×2+6×2+6×2+2×2=40(cm²).(13分)
23.解: (1)(5. 32 )(3分)
提示:因为-2+1=-1,(-2)×1-1=-3, 所以(-2，1)不是“共生有理数对”；因为 5+32=132,5×32 -1=132,所以(5. 32 )是“共生有理数对”.
(2)因为(a，3)是“共生有理数对”，所以 3+a=3a -1,解得a=2.(8分)
(3)(-n,-m)不是“共生有理数对”.(10分)
理由如下：
因为(m,n)是“共生有理数对”,所以m+n= mn -1,
所以-m-n=-(m+n)=-mn+1,所以(-n.-m)不是“共生有理数对”.(14分)