广东省广州市第九十七中学2024-2025学年九年级上学期期中数学试卷

这是一份广东省广州市第九十七中学2024-2025学年九年级上学期期中数学试卷，共20页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

1．（3分）下列交通标志中，是中心对称图形的是（ ）
A．B．C．D．
2．（3分）下列方程是一元二次方程的是（ ）
A．ax2+bx+c＝0B．（x﹣1）（x﹣2）＝0
C．3x2﹣5xy+y2＝0D．
3．（3分）一元二次方程（x﹣5）（x+6）＝0的根是（ ）
A．x＝﹣5B．x＝﹣6
C．x1＝5，x2＝﹣6D．x1＝﹣5，x2＝6
4．（3分）抛物线的顶点坐标是（ ）
A．（4，﹣2）B．（4，2）C．（﹣4，﹣2）D．（﹣4，2）
5．（3分）把抛物线y＝﹣3x2+2向右平移2个单位，向下平移1个单位，得到的抛物线是（ ）
A．y＝﹣3（x﹣2）2﹣1B．y＝﹣3（x+2）2﹣1
C．y＝﹣3（x+2）2+1D．y＝﹣3（x﹣2）2+1
6．（3分）如图，△ABC绕点A旋转一定角度得到△ADE，则BC＝4，AC＝3，则下列说法正确的是（ ）
A．DE＝3B．AE＝4
C．∠CAB是旋转角D．∠CAE是旋转角
7．（3分）关于x的方程ax2+8x﹣c＝0的两根为1和﹣3，则a，c的值分别为（ ）
A．a＝4，c＝﹣12B．a＝4，c＝12
C．a＝﹣4，c＝12D．a＝﹣4，c＝﹣12
8．（3分）已知二次函数y＝ax2+bx的图象经过点（﹣2，8）和（﹣1，5），这个二次函数的表达式为（ ）
A．y＝﹣x2+6xB．y＝x2+6xC．y＝﹣x2﹣6xD．y＝x2﹣6x
9．（3分）有一块长32cm，宽24cm的长方形纸片，在每个角上截去相同的正方形，再折起来做成一个无盖的盒子，已知盒子的底面积是原纸片面积的一半，则盒子的高是（ ）
A．3cmB．2cmC．5cmD．4cm
10．（3分）如图，Rt△OAB的顶点A（﹣2，4）在抛物线y＝ax2上，将Rt△OAB绕点O顺时针旋转90°，得到△OCD，边CD与该抛物线交于点P，则点P的坐标为（ ）
A．（，）B．（2，2）C．（，2）D．（2，）
二、填空题（本题有6个小题，每小题3分，共18分）
11．（3分）方程x2﹣25＝0的解为 ．
12．（3分）在平面直角坐标系内，若点P（p，﹣2）和点Q（6，q）关于原点O对称，则p+q的值为 ．
13．（3分）抛物线y＝x2+6x﹣8的对称轴为直线 ．
14．（3分）如图，△ODC是由△OAB绕点O顺时针旋转40°后得到的图形，若点D恰好落在AB上，且∠AOC＝105°，则∠C的度数是 ．
15．（3分）如图，花坛水池中央有一喷泉，水管OP＝3m，水从喷头P喷出后呈抛物线状先向上至最高点后落下，若最高点距水面4m，P距抛物线对称轴1m，则为使水不落到池外，水池半径最小为 ．
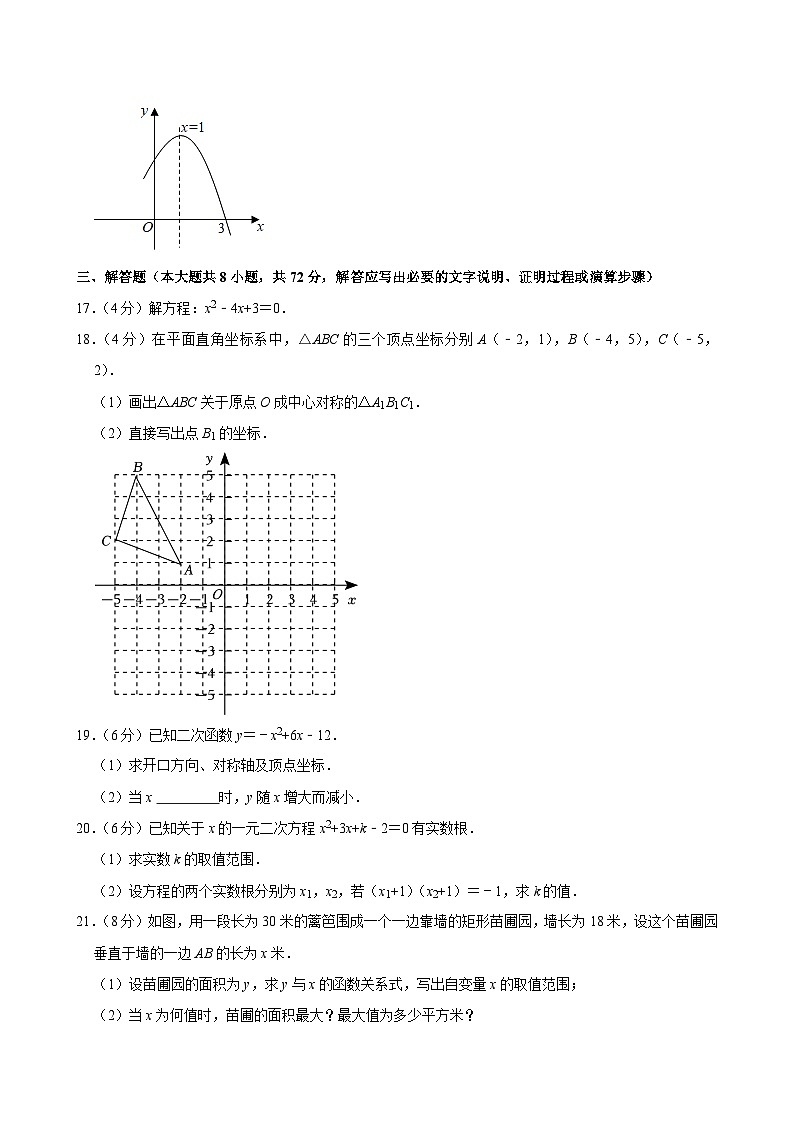
16．（3分）如图是抛物线y＝ax2+bx+c的部分图象，图象过点（3，0），对称轴为直线x＝1，有下列四个结论：①abc＞0；②a﹣b+c＝0；③y的最大值为3；④方程ax2+bx+c+1＝0有实数根．其中正确的为 （将所有正确结论的序号都填入）．
三、解答题（本大题共8小题，共72分，解答应写出必要的文字说明、证明过程或演算步骤）
17．（4分）解方程：x2﹣4x+3＝0．
18．（4分）在平面直角坐标系中，△ABC的三个顶点坐标分别A（﹣2，1），B（﹣4，5），C（﹣5，2）．
（1）画出△ABC关于原点O成中心对称的△A1B1C1．
（2）直接写出点B1的坐标．
19．（6分）已知二次函数y＝﹣x2+6x﹣12．
（1）求开口方向、对称轴及顶点坐标．
（2）当x 时，y随x增大而减小．
20．（6分）已知关于x的一元二次方程x2+3x+k﹣2＝0有实数根．
（1）求实数k的取值范围．
（2）设方程的两个实数根分别为x1，x2，若（x1+1）（x2+1）＝﹣1，求k的值．
21．（8分）如图，用一段长为30米的篱笆围成一个一边靠墙的矩形苗圃园，墙长为18米，设这个苗圃园垂直于墙的一边AB的长为x米．
（1）设苗圃园的面积为y，求y与x的函数关系式，写出自变量x的取值范围；
（2）当x为何值时，苗圃的面积最大？最大值为多少平方米？
22．（10分）如图，在△ABC中，∠B＝40°，将△ABC绕着点A顺时针旋转得到△AB′C′，点C′在BC上．
（1）求证：C′A平分∠B′C′C；
（2）若AB′∥BC，求∠C的度数．
23．（10分）如图，抛物线y＝（x+m）2+k与x轴交于A、B两点，与y轴交于点C，其顶点M的坐标为（1，﹣4）．
（1）直接写出点A、B、C的坐标；
（2）若点P在抛物线上，△ABP的面积是6，求点P的坐标．
24．（12分）如图，等边△ABC中，点D是AC边上一点，连接BD，过点A作AE⊥BD于E．
（1）如图1，连接CE并延长CE交AB于点F，若∠CBD＝15°，AB＝4，
①∠BAE＝ °；
②求CE的长；
（2）如图2，当点D在线段AC的延长线上时，将线段AE绕点A逆时针旋转60°得到线段AF，连接EF，交BC于G，连接CF，求证：BG＝CG．
2024-2025学年广东省广州九十七中九年级上学期期中数学试卷
参考答案与试题解析
一、选择题（本题有10个小题，每小题3分，满分30分，下面每小题给出的四个选项中，只有一个是正确的）
1．（3分）下列交通标志中，是中心对称图形的是（ ）
A．B．C．D．
【答案】A
【分析】在平面内，把一个图形绕某个点旋转180°，如果旋转后的图形能与原来的图形重合，那么这个图形就是中心对称图形，据此进行判断即可．
【解答】解：选项B、C、D的图形均不能找到这样的一个点，使图形绕某一点旋转180度后和原图形完全重合，所以不是中心对称图形；
选项A的图形能找到这样的一个点，使图形绕某一点旋转180度后和原图形完全重合，所以是中心对称图形．
故选：A．
2．（3分）下列方程是一元二次方程的是（ ）
A．ax2+bx+c＝0B．（x﹣1）（x﹣2）＝0
C．3x2﹣5xy+y2＝0D．
【答案】B
【分析】一元二次方程必须满足三个条件：（1）未知数的最高次数是2；（2）二次项系数不为0；（3）是整式方程；由此判断即可．
【解答】解：A．当a＝0时，ax2+bx+1＝0不是一元二次方程，故此选项不符合题意；
B．（x﹣1）（x﹣2）＝0是一元二次方程，故此选项符合题意；
C．3x2﹣5xy+y2＝0，含有两个未知数，不是一元二次方程，故此选项不符合题意；
D．该方程是分式方程，不是一元二次方程，故此选项不符合题意；
故选：B．
3．（3分）一元二次方程（x﹣5）（x+6）＝0的根是（ ）
A．x＝﹣5B．x＝﹣6
C．x1＝5，x2＝﹣6D．x1＝﹣5，x2＝6
【答案】C
【分析】方程左边是两个式子相乘且右边为0的形式，所以让每个式子分别为0，直接解答．
【解答】解：由题知x﹣5＝0或x+6＝0
所以x1＝5，x2＝﹣6．
故选：C．
4．（3分）抛物线的顶点坐标是（ ）
A．（4，﹣2）B．（4，2）C．（﹣4，﹣2）D．（﹣4，2）
【答案】B
【分析】依据题意，根据其顶点式可以判断得解．
【解答】解：由题意，∵抛物线为，
∴其的顶点为（4，2）．
故选：B．
5．（3分）把抛物线y＝﹣3x2+2向右平移2个单位，向下平移1个单位，得到的抛物线是（ ）
A．y＝﹣3（x﹣2）2﹣1B．y＝﹣3（x+2）2﹣1
C．y＝﹣3（x+2）2+1D．y＝﹣3（x﹣2）2+1
【答案】D
【分析】根据函数图象平移的法则解答即可．
【解答】解：抛物线y＝﹣3x2+2向右平移2个单位，向下平移1个单位，得到的抛物线是y＝﹣3（x﹣2）2+2﹣1，即y＝﹣3（x﹣2）2+1．
故选：D．
6．（3分）如图，△ABC绕点A旋转一定角度得到△ADE，则BC＝4，AC＝3，则下列说法正确的是（ ）
A．DE＝3B．AE＝4
C．∠CAB是旋转角D．∠CAE是旋转角
【答案】D
【分析】根据旋转的定义和三角形的性质即可求解．
【解答】解：∵△ABC绕点A旋转一定角度得到△ADE，BC＝4，AC＝3．
∴DE＝BC＝4；AE＝AC＝3；∠CAE是旋转角．故选D．
7．（3分）关于x的方程ax2+8x﹣c＝0的两根为1和﹣3，则a，c的值分别为（ ）
A．a＝4，c＝﹣12B．a＝4，c＝12
C．a＝﹣4，c＝12D．a＝﹣4，c＝﹣12
【答案】A
【分析】利用根与系数关系构建方程求解．
【解答】解：∵关于x的方程ax2+8x﹣c＝0的两根为1和﹣3，
∴1+（﹣3）＝﹣，1×（﹣3）＝﹣，
∴a＝4，c＝﹣12，
故选：A．
8．（3分）已知二次函数y＝ax2+bx的图象经过点（﹣2，8）和（﹣1，5），这个二次函数的表达式为（ ）
A．y＝﹣x2+6xB．y＝x2+6xC．y＝﹣x2﹣6xD．y＝x2﹣6x
【答案】C
【分析】由给定点的坐标，利用待定系数法，即可求出这个二次函数的表达式．
【解答】解：将（﹣2，8），（﹣1，5）代入y＝ax2+bx得：，
解得：，
∴这个二次函数的表达式为y＝﹣x2﹣6x．
故选：C．
9．（3分）有一块长32cm，宽24cm的长方形纸片，在每个角上截去相同的正方形，再折起来做成一个无盖的盒子，已知盒子的底面积是原纸片面积的一半，则盒子的高是（ ）
A．3cmB．2cmC．5cmD．4cm
【答案】D
【分析】本题应设盒子的高为x cm，那么截去的正方形的边长也为x cm，从而可用含有x的代数式表示盒子底面周长是（32﹣2x）cm，宽是（24﹣2x）cm，根据长方形的面积等于长×宽，即可列出方程，求出答案．
【解答】解：设盒子的高为x cm，
则其底面长为（32﹣2x）cm，宽为（24﹣2x）cm，
底面面积为（32﹣2x）（24﹣2x）cm2．
则（32﹣2x）（24﹣2x）＝×32×24
整理，得x2﹣28x+96＝0
解之，得x1＝4，x2＝24．
当x＝24时不合题意，应舍去．
故选：D．
10．（3分）如图，Rt△OAB的顶点A（﹣2，4）在抛物线y＝ax2上，将Rt△OAB绕点O顺时针旋转90°，得到△OCD，边CD与该抛物线交于点P，则点P的坐标为（ ）
A．（，）B．（2，2）C．（，2）D．（2，）
【答案】C
【分析】首先根据点A在抛物线y＝ax2上求得抛物线的解析式和线段OB的长，从而求得点D的坐标，根据点P的纵坐标和点D的纵坐标相等得到点P的坐标即可；
【解答】解：∵Rt△OAB的顶点A（﹣2，4）在抛物线y＝ax2上，
∴4＝a×（﹣2）2，
解得：a＝1
∴解析式为y＝x2，
∵Rt△OAB的顶点A（﹣2，4），
∴OB＝OD＝2，
∵Rt△OAB绕点O顺时针旋转90°，得到△OCD，
∴CD∥x轴，
∴点D和点P的纵坐标均为2，
∴令y＝2，得2＝x2，
解得：x＝±，
∵点P在第一象限，
∴点P的坐标为：（，2）
故选：C．
二、填空题（本题有6个小题，每小题3分，共18分）
11．（3分）方程x2﹣25＝0的解为 x＝±5 ．
【答案】见试题解答内容
【分析】移项得x2＝25，然后采用直接开平方法即可得到方程的解．
【解答】解：∵x2﹣25＝0，
移项，得 x2＝25，
∴x＝±5．
故答案为：x＝±5．
12．（3分）在平面直角坐标系内，若点P（p，﹣2）和点Q（6，q）关于原点O对称，则p+q的值为 ﹣4 ．
【答案】﹣4．
【分析】根据关于原点对称的两点，横坐标和纵坐标都互为相反数即可求解．
【解答】解：∵点P（p，﹣2）和点Q（6，q）关于原点O对称，
∴p＝﹣6，q＝2，
∴p+q＝﹣4，
故答案为：﹣4．
13．（3分）抛物线y＝x2+6x﹣8的对称轴为直线 x＝﹣3 ．
【答案】x＝﹣3．
【分析】依据题意，由抛物线为y＝x2+6x﹣8＝（x+3）2﹣17，从而可以判断得解．
【解答】解：由题意，∵抛物线为y＝x2+6x﹣8＝（x+3）2﹣17，
∴对称轴是直线x＝﹣3．
故答案为：x＝﹣3．
14．（3分）如图，△ODC是由△OAB绕点O顺时针旋转40°后得到的图形，若点D恰好落在AB上，且∠AOC＝105°，则∠C的度数是 45° ．
【答案】见试题解答内容
【分析】先根据∠AOC的度数和∠BOC的度数，可得∠AOB的度数，再根据△AOD中，AO＝DO，可得∠A的度数，进而得出△ABO中∠B的度数，可得∠C的度数．
【解答】解：∵∠AOC的度数为105°，
由旋转可得∠AOD＝∠BOC＝40°，
∴∠AOB＝105°﹣40°＝65°，
∵△AOD中，AO＝DO，
∴∠A＝（180°﹣40°）＝70°，
∴△ABO中，∠B＝180°﹣70°﹣65°＝45°，
由旋转可得，∠C＝∠B＝45°，
故答案为：45°．
15．（3分）如图，花坛水池中央有一喷泉，水管OP＝3m，水从喷头P喷出后呈抛物线状先向上至最高点后落下，若最高点距水面4m，P距抛物线对称轴1m，则为使水不落到池外，水池半径最小为 3米 ．
【答案】见试题解答内容
【分析】首先建立坐标系，然后利用待定系数法求得函数的解析式，然后令y＝0，即可求解．
【解答】解：如图建立坐标系．
抛物线的顶点坐标是（1，4），
设抛物线的解析式是y＝a（x﹣1）2+4，
把（0，3）代入解析式得：a+4＝3，
解得：a＝﹣1．
则抛物线的解析式是：y＝﹣（x﹣1）2+4．
当y＝0时，﹣（x﹣1）2+4＝0，
解得：x1＝3，x2＝﹣1（舍去）．
则水池的最小半径是3米．
故答案为：3米．
16．（3分）如图是抛物线y＝ax2+bx+c的部分图象，图象过点（3，0），对称轴为直线x＝1，有下列四个结论：①abc＞0；②a﹣b+c＝0；③y的最大值为3；④方程ax2+bx+c+1＝0有实数根．其中正确的为 ②④ （将所有正确结论的序号都填入）．
【答案】见试题解答内容
【分析】由抛物线的开口方向判断a与0的关系，由抛物线与y轴的交点判断c与0的关系，然后根据对称轴判定b与0的关系；当x＝﹣1时，y＝a﹣b+c；然后由图象确定当y＝﹣1时，x的值有2个．
【解答】解：∵抛物线开口向下，
∴a＜0，
∵对称轴x＝﹣＝1，
∴b＝﹣2a＞0，
∵抛物线与y轴的交点在y轴正半轴，
∴c＞0，
∴abc＜0，故①错误；
∵抛物线与x轴的交点（3，0），对称轴为直线x＝1，
∴抛物线x轴的另一个交点在（﹣1，0），
∴当x＝﹣1时，y＝a﹣b+c＝0，即②正确；
由图象无法判断y的最大值，故③错误；
方程ax2+bx+c+1＝0的根的个数，可看作二次函数y＝ax2+bx+c与y＝﹣1的图象的交点个数，
由图象可知，必然有2个交点，即方程ax2+bx+c+1＝0有2个不相等的实数根．
故④正确．
故答案为：②④．
三、解答题（本大题共8小题，共72分，解答应写出必要的文字说明、证明过程或演算步骤）
17．（4分）解方程：x2﹣4x+3＝0．
【答案】见试题解答内容
【分析】利用因式分解法解出方程．
【解答】解：x2﹣4x+3＝0
（x﹣1）（x﹣3）＝0
x﹣1＝0或x﹣3＝0
x1＝1，x2＝3．
18．（4分）在平面直角坐标系中，△ABC的三个顶点坐标分别A（﹣2，1），B（﹣4，5），C（﹣5，2）．
（1）画出△ABC关于原点O成中心对称的△A1B1C1．
（2）直接写出点B1的坐标．
【答案】（1）作图见解答过程；
（2）B1（4，﹣5）．
【分析】（1）利用关于原点对称的点的坐标特征得到A1、B1、C1的坐标，然后描点得到△A1B1C1；
（2）根据关于原点对称的点的坐标特征写出点B1的坐标．
【解答】解：（1）如图，△A1B1C1为所作；
（2）由图可知，B1（4，﹣5）．
19．（6分）已知二次函数y＝﹣x2+6x﹣12．
（1）求开口方向、对称轴及顶点坐标．
（2）当x ＞3 时，y随x增大而减小．
【答案】（1）开口方向向下，对称轴是直线x＝3，顶点为（3，﹣3）；（2）＞3．
【分析】（1）依据题意，由二次函数为y＝﹣x2+6x﹣12＝﹣（x﹣3）2﹣3，从而可得开口方向向下，对称轴是直线x＝3，顶点为（3，﹣3），进而得解；
（2）依据题意，由（1）y＝﹣（x﹣3）2﹣3，从而当x＞3时，y随x增大而减小，进而得解．
【解答】解：（1）由题意，∵二次函数为y＝﹣x2+6x﹣12＝﹣（x﹣3）2﹣3，
∴开口方向向下，对称轴是直线x＝3，顶点为（3，﹣3）．
（2）由题意，由（1）y＝﹣（x﹣3）2﹣3，
∴当x＞3时，yy随x增大而减小．
故答案为：＞3．
20．（6分）已知关于x的一元二次方程x2+3x+k﹣2＝0有实数根．
（1）求实数k的取值范围．
（2）设方程的两个实数根分别为x1，x2，若（x1+1）（x2+1）＝﹣1，求k的值．
【答案】见试题解答内容
【分析】（1）根据一元二次方程x2+3x+k﹣2＝0有实数根，可知Δ≥0，即可求得k的取值范围；
（2）根据根与系数的关系和（x1+1）（x2+1）＝﹣1，可以求得k的值．
【解答】解：（1）∵关于x的一元二次方程x2+3x+k﹣2＝0有实数根，
∴Δ＝32﹣4×1×（k﹣2）≥0，
解得k≤，
即k的取值范围是k≤；
（2）∵方程x2+3x+k﹣2＝0的两个实数根分别为x1，x2，
∴x1+x2＝﹣3，x1x2＝k﹣2，
∵（x1+1）（x2+1）＝﹣1，
∴x1x2+（x1+x2）+1＝﹣1，
∴k﹣2+（﹣3）+1＝﹣1，
解得k＝3，
即k的值是3．
21．（8分）如图，用一段长为30米的篱笆围成一个一边靠墙的矩形苗圃园，墙长为18米，设这个苗圃园垂直于墙的一边AB的长为x米．
（1）设苗圃园的面积为y，求y与x的函数关系式，写出自变量x的取值范围；
（2）当x为何值时，苗圃的面积最大？最大值为多少平方米？
【答案】（1）y＝﹣2x2+30x，0＜x≤6；（2）当x＝时，这个苗圃园的面积有最大值，最大值是平方米．
【分析】（1）根据题意和图形，y与x的函数关系式，注意墙长是18米；
（2）根据题意和图形，可以得到S与x的函数关系式，再根据二次函数的性质，即可求得当x取何值时，这个苗圃园的面积有最大值，最大值是多少．
【解答】解：（1）由题意可得，
y＝x（30﹣2x）＝﹣2x2+30x，
x＞0，30﹣2x≤18，
0＜x≤6；
（2）设这个苗圃园的面积为S平方米，
由题意可得，
S＝x（30﹣2x）＝﹣2（x﹣）2+，
∵平行于墙的一边长＞0米，且不大于18米，
∴0≤30﹣2x≤18，
解得，6≤x≤15，
∴当x＝时，S取得最大值，此时S＝，
答：当x＝时，这个苗圃园的面积有最大值，最大值是平方米．
22．（10分）如图，在△ABC中，∠B＝40°，将△ABC绕着点A顺时针旋转得到△AB′C′，点C′在BC上．
（1）求证：C′A平分∠B′C′C；
（2）若AB′∥BC，求∠C的度数．
【答案】（1）证明见解答；
（2）∠C的度数是70°．
【分析】（1）由旋转得AC′＝AC，∠AC′B′＝∠C，则∠AC′C＝∠C，所以∠AC′B′＝∠AC′C，即C′A平分∠B′C′C；
（2）由∠B′＝∠B＝40°，AB′∥BC，得∠B′C′B＝∠B′＝40°，则2∠AC′C＝140°，求得∠AC′C＝70°，所以∠C＝∠AC′C＝70°．
【解答】（1）证明：∵将△ABC绕着点A顺时针旋转得到△AB′C′，
∴AC′＝AC，∠AC′B′＝∠C，
∵点C′在BC上，
∴∠AC′C＝∠C，
∴∠AC′B′＝∠AC′C，
∴C′A平分∠B′C′C．
（2）解：∵∠B′＝∠B＝40°，AB′∥BC，
∴∠B′C′B＝∠B′＝40°，
∴∠AC′B′+∠AC′C＝2∠AC′C＝180°﹣40°＝140°，
∴∠AC′C＝70°，
∴∠C＝∠AC′C＝70°，
∴∠C的度数是70°．
23．（10分）如图，抛物线y＝（x+m）2+k与x轴交于A、B两点，与y轴交于点C，其顶点M的坐标为（1，﹣4）．
（1）直接写出点A、B、C的坐标；
（2）若点P在抛物线上，△ABP的面积是6，求点P的坐标．
【答案】（1）A（﹣1，0），B（3，0），C（0，﹣3）；
（2）点P的坐标为（，3）或（1+，3）或（0，﹣3）或（2，﹣3）．
【分析】（1）根据坐标轴上点的特征分别令x＝0，y＝0，即可求得A，B，C三点的坐标；
（2）设P（t，t2﹣2t﹣3）根据三角形面积公式计算即可．
【解答】解：（1）∵抛物线顶点M的坐标为（1，﹣4），
∴抛物线解析式为y＝（x﹣1）2﹣4＝x2﹣2x﹣3，
在y＝（x﹣1）2﹣4中，令y＝0，得0＝（x﹣1）2﹣4，解得：x1＝﹣1，x2＝3，
∴A（﹣1，0），B（3，0），
令x＝0，得y＝﹣3
∴C（0，﹣3）；
（2）设P（t，t2﹣2t﹣3）
∵S△PAB＝6，
∴×4|t2﹣2t﹣3|＝6，即|t2﹣2t﹣3|＝3，
当t2﹣2t﹣3＝3时，
解得：t1＝1﹣，t2＝1+，
当t2﹣2t﹣3＝﹣3时，
解得：t3＝0，t4＝2，
∴点P的坐标为（，3）或（1+，3）或（0，﹣3）或（2，﹣3）．
24．（12分）如图，等边△ABC中，点D是AC边上一点，连接BD，过点A作AE⊥BD于E．
（1）如图1，连接CE并延长CE交AB于点F，若∠CBD＝15°，AB＝4，
①∠BAE＝ 45 °；
②求CE的长；
（2）如图2，当点D在线段AC的延长线上时，将线段AE绕点A逆时针旋转60°得到线段AF，连接EF，交BC于G，连接CF，求证：BG＝CG．
【答案】（1）①45；
②CE＝2﹣2；
（2）证明见解答过程．
【分析】（1）①由∠CBD＝15°可得∠ABE＝45°，结合AE⊥BD，可得∠BAE＝∠ABE＝45°；
②由∠BAE＝∠ABE＝45°得到AE＝BE，结合AC＝BC，得到CF是AB的垂直平分线，由AB＝4可求EF，CF的长，即可求CE的长；
（2）过点M作CM∥BD，通过将线段AE绕点A逆时针旋转60°得到线段AF，可得AE＝AF，∠BAE＝∠CAF，证明△ABE≌△ACF，可得BE＝CF，∠BEM＝150°，∠CFM＝30°，由CM∥BD，可证∠CME＝150°，即∠FMC＝30°，可证CF＝CM＝BE，然后可证△BGE≌△CGM，进而得证．
【解答】（1）解：①∵△ABC为等边三角形，
∴AB＝BC＝AC＝4，∠BAC＝60°，
∵∠DBC＝15°，
∴∠ABE＝45°，
∵AE⊥BD，
∴∠BAE＝∠ABE＝45°，
故答案为：45；
②由（1）知∠BAE＝∠ABE＝45°，
∴AE＝BE，
∵AC＝BC，
∴CF垂直平分AB即AF＝BF＝2，CF⊥AB，
∵∠ABE＝45°，
∴∠FEB＝∠ABE＝45°，
∴BF＝EF＝2，
在Rt△BCF中，由勾股定理得：CF＝＝2，
∴CE＝2﹣2；
（2）证明：如图2：过点C作CM∥BD，
∵将线段AE绕点A逆时针旋转60°得到线段AF，
∴AE＝AF，∠EAF＝60°，
∴△AEF为等边三角形，
∴∠AFE＝∠AEF＝60°，
∴∠FAC+∠EAC＝60°，
∵∠BAE+∠EAC＝60°，
∴∠BAE＝∠CAF，
∵AB＝AC，AE＝AF，
∴△ABE≌△ACF（SAS），
∴BE＝CF，∠AEB＝∠AFC＝90°，
∴∠BEF＝150°，∠MFC＝30°，
∵MC∥BD，
∴∠BEF＝∠GMC＝150°，
∴∠CMF＝30°＝∠CFM，
∴CM＝CF，
∵CF＝BE，
∴BE＝CM，
∵∠BGE＝∠CGM，∠BEG＝∠CMG，
∴△BGE≌△CGM（AAS），
∴BG＝CG．