山西省阳泉市盂县2024-2025学年八年级上学期11月期中考试数学试题

这是一份山西省阳泉市盂县2024-2025学年八年级上学期11月期中考试数学试题，共12页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

（全卷共三大题，共6页，满分120分，考试时间120分钟）
第I卷（选择题共30分）
一、选择题（每小题3分，共30分）
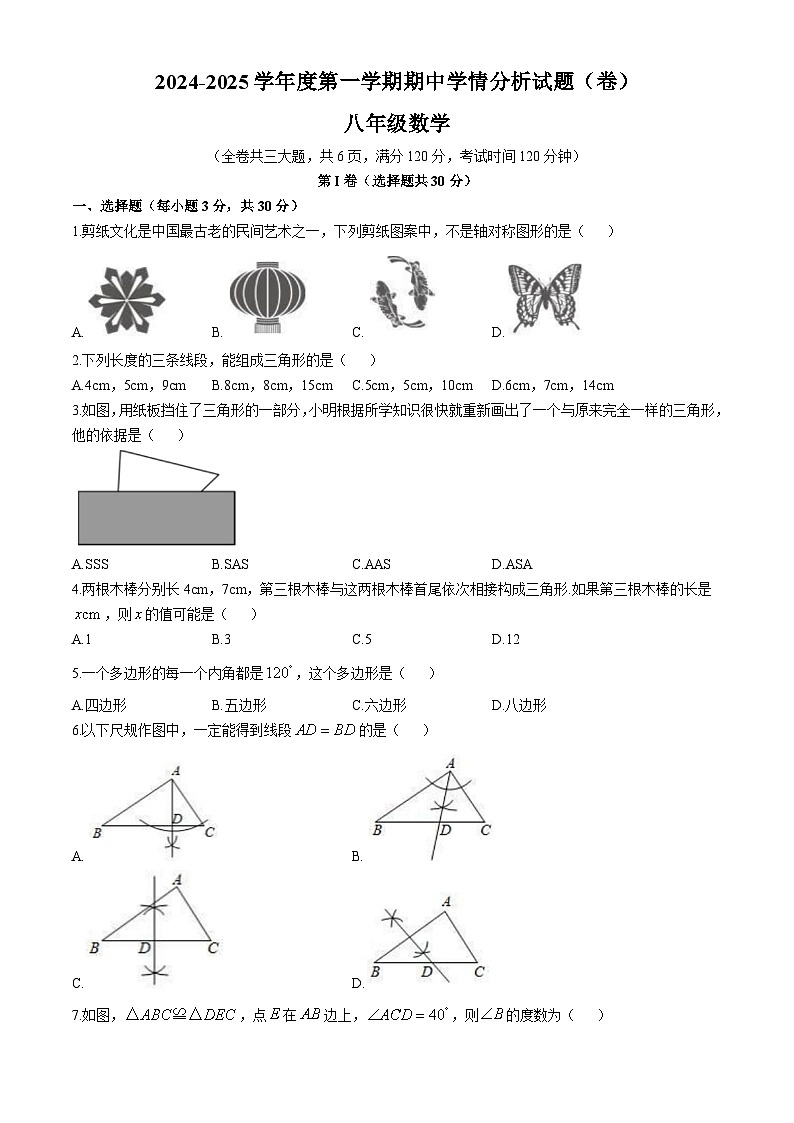
1.剪纸文化是中国最古老的民间艺术之一，下列剪纸图案中，不是轴对称图形的是（ ）
A.B.C.D.
2.下列长度的三条线段，能组成三角形的是（ ）
A.4cm，5cm，9cmB.8cm，8cm，15cmC.5cm，5cm，10cmD.6cm，7cm，14cm
3.如图，用纸板挡住了三角形的一部分，小明根据所学知识很快就重新画出了一个与原来完全一样的三角形，他的依据是（ ）
A.SSSB.SASC.AASD.ASA
4.两根木棒分别长4cm，7cm，第三根木棒与这两根木棒首尾依次相接构成三角形.如果第三根木棒的长是，则的值可能是（ ）
A.1B.3C.5D.12
5.一个多边形的每一个内角都是，这个多边形是（ ）
A.四边形B.五边形C.六边形D.八边形
6.以下尺规作图中，一定能得到线段的是（ ）
A.B.
C.D.
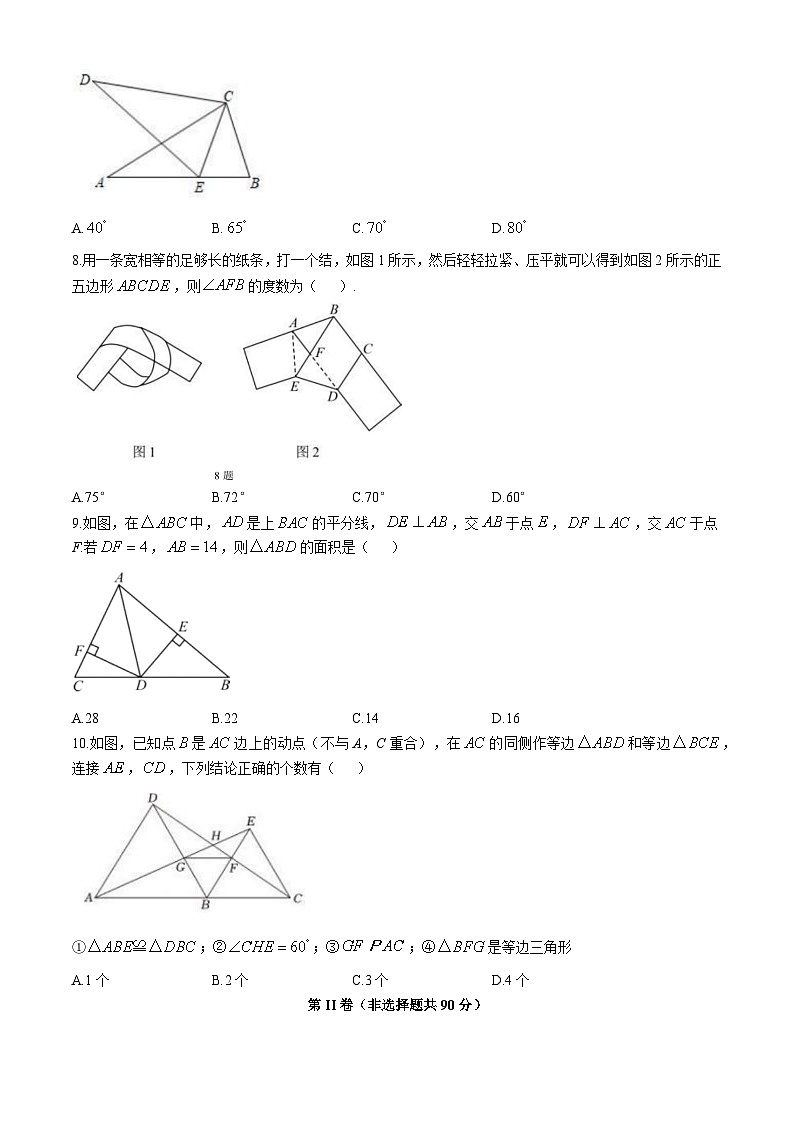
7.如图，，点在边上，，则的度数为（ ）
A.B.C.D.
8.用一条宽相等的足够长的纸条，打一个结，如图1所示，然后轻轻拉紧、压平就可以得到如图2所示的正五边形，则的度数为（ ）.
A.75°B.72°C.70°D.60°
9.如图，在中，是上的平分线，，交于点，，交于点F.若，，则的面积是（ ）
A.28B.22C.14D.16
10.如图，已知点是边上的动点（不与A，C重合），在的同侧作等边和等边，连接，，下列结论正确的个数有（ ）
①；②；③；④是等边三角形
A.1个B.2个C.3个D.4个
第II卷（非选择题共90分）
二、填空题：（本大题共5小题，每小题3分，共15分）.
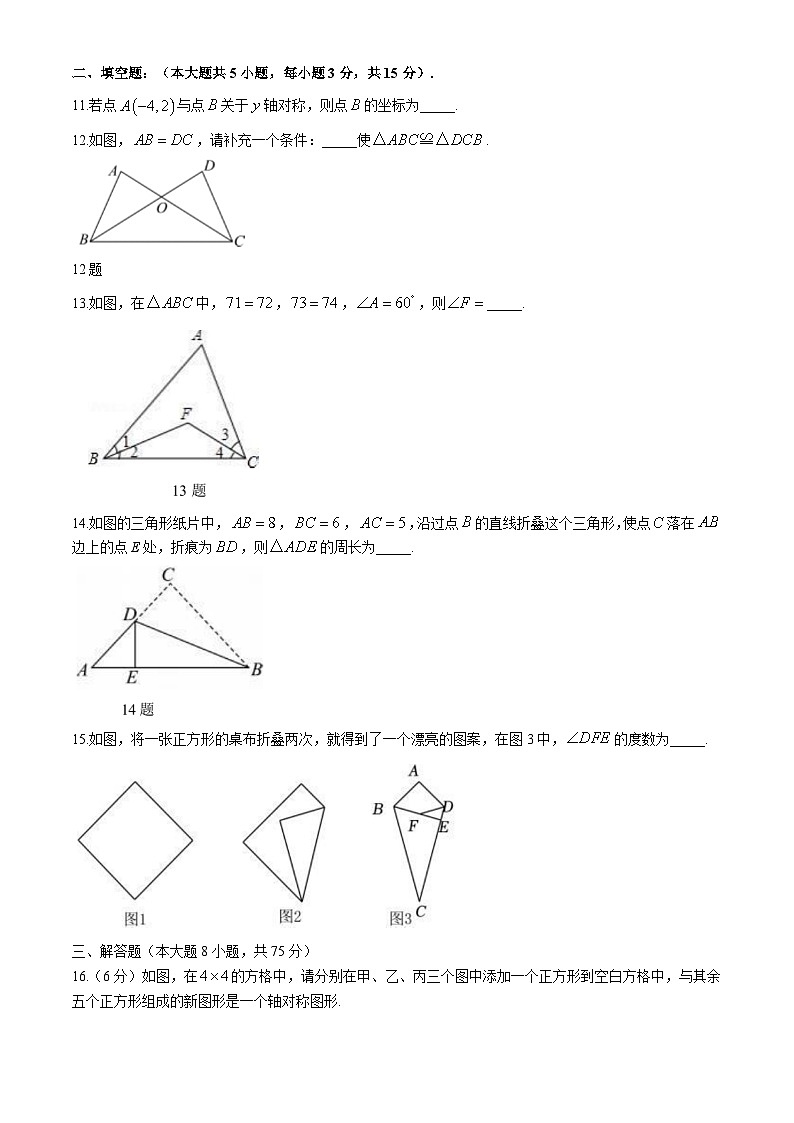
11.若点与点关于轴对称，则点的坐标为_____.
12.如图，，请补充一个条件：_____使.
12题
13.如图，在中，，，，则_____.
14.如图的三角形纸片中，，，，沿过点的直线折叠这个三角形，使点落在边上的点E处，折痕为，则的周长为_____.
15.如图，将一张正方形的桌布折叠两次，就得到了一个漂亮的图案，在图3中，的度数为_____.
三、解答题（本大题8小题，共75分）
16.（6分）如图，在的方格中，请分别在甲、乙、丙三个图中添加一个正方形到空白方格中，与其余五个正方形组成的新图形是一个轴对称图形.
17.（8分）请根据对话回答问题：
（1）小明为什么说这个凸多边形的内角和不可能是2022?
（2）小敏求的是几边形的内角和?
18.（8分）（1）作出关于轴对称的图形，并写出点的坐标：_____；
（2）在轴上找一点，使得最小（画出图形，找到点的位置）.
（3）求的面积.
19.（8分）如图，B，C，E三点在同一条直线上，，，，求证：
（1）；
（2）若。，求的度数.
20.（10分）阅读与思考
请阅读下面小论文，并完成相应的学习任务.
任务：
（1）上面小论文中提到“对于正边形，从一个顶点出发作对角线，它们将边形分成个三角形，得到其内角和是”，其中体现的数学思想主要是_____.（填出字母代号即可）
A.数形结合思想B.转化思想C.方程思想
（2）图3中的度数为_____.
（3）除“正三角形”“正四边形”外，请你再写出一种可以进行密铺的正多边形
（4）图6是图5中的一个基本图形，其中，，求的度数.
21.（10分）如图，四边形中，，平分，于点，的延长线于点E.
（1）求证：
（2）若，，请直接写出的长.
22.（12分）如图：是边长为6的等边三角形，是边上一动点.由点向点运动（P与点、不重合），点同时以点相同的速度，由点向延长线方向运动（点不与点重合），过点作于点，连接交于点.
（1）若设的长为，则_____，_____.
（2）当时，求的长；
（3）过点作交延长线于点，则，有怎样的关系?请说明理由.
23.（13分）阅读理解，自主探究：“一线三垂直”模型是“一线三等角”模型的特殊情况，即三个等角角度为，于是有三组边相互垂直.所以称为“一线三垂直模型”.当模型中有一组对应边长相等时，则模型中必定存在全等三角形.
（1）问题解决：如图1，在等腰直角中，，，过点作直线，于，于，求证：；
（2）问题探究：如图2，在等腰直角中，，，过点作直线于，于，，，求的长；
（3）拓展延伸：如图3，在平面直角坐标系中，，，为等腰直角三角形，，，求点坐标.
2024—2025学年度第一学期期中学情分析试题（卷）
八年级数学
（全卷共三大题，共6页，满分120分，考试时间120分钟）
一、选择题（本大题共10个小题，每小题3分，共30分）.
二、填空题（本大题共5个小题，每小题3分，共15分）
11.12.（或）
13.14.715.
三、解答题（本大题共8个小题，共75分）.
16.（共6分，每个2分）
解：如图所示.（答案不唯一）
17.（8分）
（1）解：边形的内角和为，
多边形的内角和一定是的正整数倍，
，
这个凸多边形的内角和不可能是；……4分
（2）解：设小敏求的是边形得内角和，由题意得；
.
答：小敏求的是十三边形的内角和.…………8分
18.（8分）（1）解：关于轴对称的图形如图所示，且；
……3分
（2）解：连接，与轴交点即为所求，如图所示；
……6分
（3）.
19.（8分）（1）证明：，
，，
又，
，
在和中，
，
（AAS），……5分
（2），
，
.…………8分
20.（10分）（1）B…………2分
（2）…………4分
（3）如：正六边形（答案不唯一）…………6分
（4）解：五边形的内角和为：
…………10分
21..解：平分，，

在和中
…………4分
…………5分
…………6分
（2）…………10分
22.（12分）（1），…………2分
（2）解：是边长为6的等边三角形，
，
，
，…………3分
是直角三角形，
，
，…………4分
解得：，
；…………6分
（3）.理由如下：…………7分
，
点、速度相同，
，…………8分
是等边三角形，
，…………9分
在和中，
…………10分
…………12分
23.（13分）解：（1）证明：，，
，
，
，
，
，……2分
在和中，
；…………4分
（2），，
，
，
，
，
，…………6分
在和中，
，……7分
，，
即的长为0.8cm；…………8分
（3）如图3，过点C作直线轴，交y轴于点，过作于点，过B作于点F，交x轴于点则
……9分
，
，，
…………10分
，
…………11分
在和中，
…………12分
，
点坐标为…………13分
关于同一种正多边系的平面密铺
平面密铺是指用一些形状大小完全相同的一种或几种平面图形进行拼接，彼此之间不留空隙，不重叠地把平面的一部分定全覆盖，一般来说，构成一个平面密铺图形的基本图形是多边形或类似的一些常规形状，例如我们铺设地板时经常使用正方形地砖。
对于正边形，从一个顶点出发作对角线，它们将边形分成个三角形，得到其内角和是，则一个内角的度就是，如果一个内角度数能整除，那么这样的正边形其可以进行平面密铺，图1而图2就是分别利用正三角形和正方形得到的两组密铺图案。如图3，按照平面密铺的条件，正五边形就不能进行平面密铺。
对于一些不规则的多边形，全等三角形或全等四边形也可以进行平面密铺。图4就是利用全等的四边形设计出的平面密铺图案。
对于不规则的凸五边形，迄今为止发现了15种能用于平面密铺的五边形，德国数学家莱因哈特（1895-1941）凭借其出色的平面几何功底与直觉，从1918年开始，陆续发现了5种五边形密铺方式。2015年，美国华盛顿大学数学教授卡西-曼夫妇发现了第15种能用于平面密铺的五边形，图5就是利用不规则的凸五边形得到的一种密铺图案。
题号
1
2
3
4
5
6
7
8
9
10
答案
C
B
D
C
C
D
C
B
A
D