辽宁省营口市鲅鱼圈区红旗镇初级中学2024-2025学年九年级上学期期中考试数学试卷

这是一份辽宁省营口市鲅鱼圈区红旗镇初级中学2024-2025学年九年级上学期期中考试数学试卷，共5页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

时间: 120分钟 满分: 120分
一、选择题：(每题3分，共30分)
1、下列方程是一元二次方程的是 ( )
A. (5-a)²=2 B.3x²+x-y²=0 C.y²=5-2y-y³ D.x-1x2+1=0
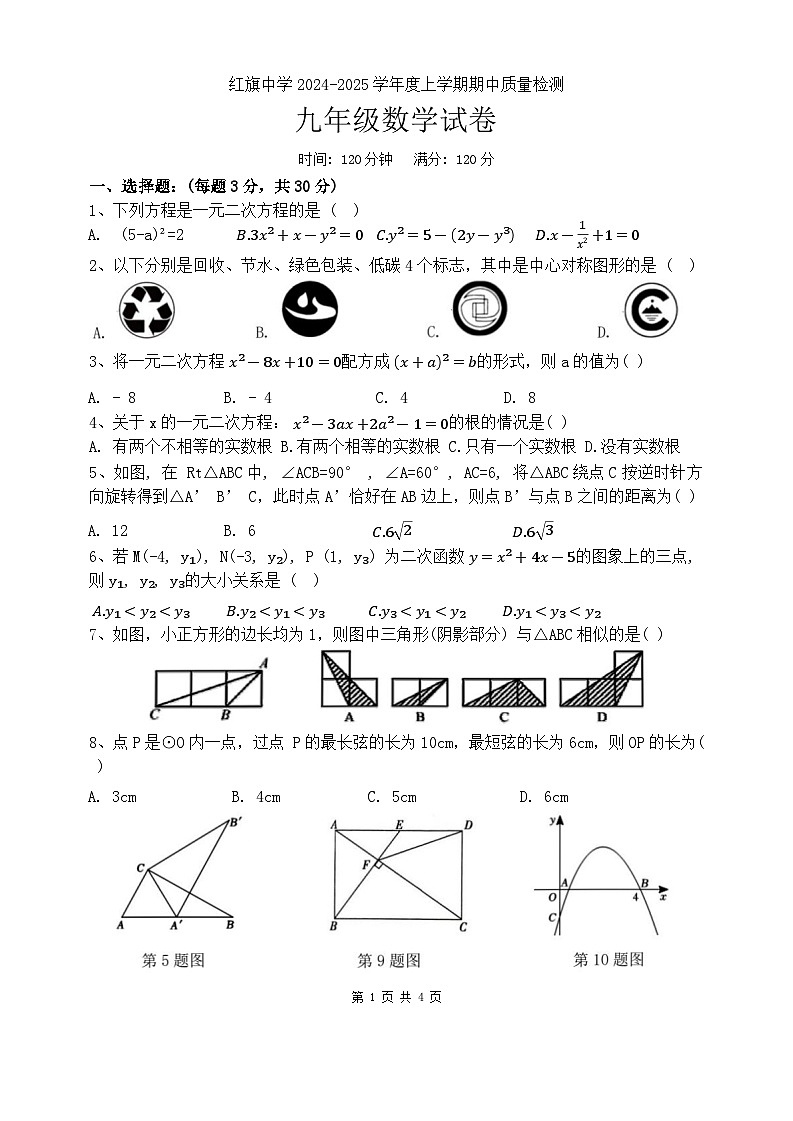
2、以下分别是回收、节水、绿色包装、低碳4个标志，其中是中心对称图形的是 ( )
3、将一元二次方程 x²-8x+10=0配方成 x+a²=b的形式，则a的值为( )
A. - 8 B. - 4 C. 4 D. 8
4、关于x的一元二次方程： x²-3ax+2a²-1=0的根的情况是( )
A. 有两个不相等的实数根 B.有两个相等的实数根 C.只有一个实数根 D.没有实数根
5、如图, 在 Rt△ABC中, ∠ACB=90° , ∠A=60°, AC=6, 将△ABC绕点C按逆时针方向旋转得到△A’ B’ C，此时点A’恰好在AB边上，则点B’与点B之间的距离为( )
A. 12 B. 6 C.62 D.63
6、若M(-4, y₁), N(-3, y₂), P (1, y₃) 为二次函数 y=x²+4x-5的图象上的三点, 则y₁, y₂, y₃的大小关系是 ( )
A.y₁7、如图，小正方形的边长均为1，则图中三角形(阴影部分) 与△ABC相似的是( )
8、点P是⊙O内一点，过点 P的最长弦的长为10cm，最短弦的长为6cm，则OP的长为( )
A. 3cm B. 4cm C. 5cm D. 6cm
第 1 页 共 4 页
9、如图所示, 在矩形ABCD中, E是AD边的中点, BE⊥AC于点F, 连接DF, 分析下列四个结论: ①△AEF∽△CAB; ②CF=2AF; ③DF=DC; ④S四边形CDEF= 52S△ABF,其中正确的结论有( )
A. 4个 B. 3个 C. 2个 D. 1个
10、如图，抛物线 y=ax²+bx+c与x轴正半轴交于A、B (4, 0) 两点, 与y轴负半轴交于点 C.①abc>0; ②4a+b>0; ③b²-4ac≥0;④若AB≥3, 则4b+3c>0;⑤若抛物线的对称轴是直线x=3, k为任意实数,则a(k-3)(k+3)≤b(3-k).上述结论中，正确的个数是( )
A. 5个 B. 4个 C. 3个 D. 2个
二、填空题：(每小题3分，共15分)
11、若一元二次方程： x²-2m+3x+m²=0有两个不相等的实数根x₁、x₂，且 x₁+x₂=x₁x₂, 则 m的值是 。
12、园林绿化处有一块长30m、宽20m的矩形空地。现计划在矩形空地的中间设计横竖道路，各与矩形的一条边平行，且横竖道路的宽度比为2：3，余下的种草坪，其中草坪的面积占这块空地面积的四分之一，若设横向道路的宽为2x m，可列方程为 。
13、如图，一下水管横截面为圆形，直径为100cm，下雨前水面宽为60cm，一场大雨过后, 水面宽为80cm, 则水位上升 cm。
14、如图, 在△ABC中, ∠ABC=90° , 把△ABC绕点B顺时针旋转90°, 得到△DBE, F是ED的中点。若AB=4, BC=6, 则线段CF的长为 。
15、规定: min{x, y}表示x和y两个数中最小值。例如:1 min{1, 3}=1, min{-2, 5, 35}=-2。则关于x的函数y= min{2x, - x-2, - x²+1}的最大值为 。
三、解答题: (共75分)
16、(10分)
(1) 解方程: x(2x--5)=4x--10 (因式分解法) (2) 化简: aa+1⋅a2-1a2+1a
17、(8分) 随着2023年杭州亚运会开幕，吉祥物“琮琮”“莲莲”“宸宸”在电商平台上爆单，在某个电商平台上9月24日的销量为5000个，9月25日和9月26日的总销量是30000个，已知9月25日和9月26日的销量较前一天的平均增长率相同。
第 2 页 共 4 页(1) 求25日、26日的销量较前一天的增长率。
(2) 某线下实体店每个吉祥物的进价为13元，售价为每个14元时，每天可售出220个，经调查，每个吉祥物涨价1元，每天将少销售20个。若销售单价不低于进价且不高于18元，则销售单价定为多少时，该实体店每天所获的利润最大? 最大利润为多少?
18、(8分)平面直角坐标系中，点A 的坐标是(0，3), 点B的坐x标是(-4, 0)。
(1)将△AOB绕点A逆时针旋转90度得到△AEF。点O、B的对应点分别是点E、F。请在图中画出△AEF。
(2) 连接BE, 以(1,0) 为位似中心, 将△ABE缩小得到△A’ B’ E’, 且位似比为2: 1, 请在x轴下方作出图形。
(3)请在x轴上找一个点 P, 使PA+PE的值最小,并直接写出P 点的坐标。
19、(8分) 如图，夜晚路灯下，小丽在点D处测得自己的影长DE=4m。在点G 处测得自己的影长DG=3m, E、D、G、B在同一条直线上。 已知小力身高为1.6m。则灯杆AB的高度为多少米?
20、(8分)如图所示, 有一块三角形余料ABC, 它的边长BC=120, 高AD=80。要把它加工为矩形形零件。
(1) 如果使矩形的长为宽的两倍，且长边在BC上，其余两个顶点分别在AB、AC上，则加工成矩形零件的长和宽分别是多少?
(2)如果要使加工的矩形零件面积最大，求矩形零件面积达到最大时的两边长。
第 3 页 共 4 页21、(8分) 综合实践课上，小李同学展示了如下的操作及问题：
(1)如图1，⊙O₁的半径为4cm，通过折叠圆形纸片，使得劣弧AB沿弦AB折叠后恰好过圆心O₁, 求AB的长;
(2) 如图2, O₂C⊥AB,垂足为点C，劣弧AB沿弦AB 折叠后经过O₂C 的中点D, AB=10cm, 求⊙O₂的半径。
22、(12分)
(1) 问题发现: 如图1, 在等腰直角△ABC中,. ∠ACB=90°BC=a。。将边AB绕点 B顺时针旋转90度得到线段 BD，连接CD，则△BCD的面积为 。(请用含a的式子表示△BCD的面积。)
(2) 类比探究: 如图2, 在一般的Rt△ABC中, ∠ACB=90°, BC=a。将边AB绕点B顺时针旋转90度得到线段BD。连接CD，则(1)中的结论是否成立，若成立请说明理由。
(3)拓展应用: 如图3, 在等腰△ABC中, AB=AC, BC=a。将边AB绕点B顺时针旋转90度得到线段BD，连接CD，试直接用含a的式子表示△BCD的面积。(不写探究过程。)
23、(13分)定义：在平面直角坐标系中，如果一个点的横、纵坐标之和为2，则称该点为“基准偶和点”。例如: (1, 1)、(-2,4)、 (6,-4) 都是“基准偶和点”。
(1)下列函数图象上只有一个“基准偶和点”的是 ；(填序号)
①y=2x+1; circle2y=21x; ③y=-x+1; ④y=x²+3x+6
(2) 已知抛物线 y=x²+mx+n(m、n均为常数) 与直线y=x+4只有一个交点，且该点是“基准偶和点”，求抛物线的解析式；
(3) 抛物线 y=ax²+bx+3(a、b均为常数，a>0) 的图象上有且只有一个“基准偶和点”，令 w=b²-6b+4a,是否存在一个常数t，使得当t≤b≤t+1时，w有最小值恰好等于-t，若存在，求出t的值，若不存在，请说明理由。
第 4 页 共 4 页