河南省信阳市淮滨县2024-2025学年上学期期中阶段性综合练习九年级数学试卷

这是一份河南省信阳市淮滨县2024-2025学年上学期期中阶段性综合练习九年级数学试卷，共8页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题。（每小题只有一个正确答案，每小题3分，共30分）
1．下列方程是一元二次方程的是( )
A. B.
C. D.
2．如图，是的直径，，则等于
A．B．C． D．
3．如图，一块等腰直角的三角板ABC，在水平桌面上绕点C按顺时针方向旋转到A′B′C的位置，使A、C、B′三点共线，那么旋转角度的大小为（ ）
A．45° B．90° C．120° D．135°
4．有一人患了流感，经过两轮传染后共有100人患了流感，每轮传染中平均一个人传染的人数x满足的方程为（ ）
A．（1+x）2=100B．x（1+x）=100C．1+x+x2=100D．x2=100
5．如图是二次函数y=ax2+bx+c图象的一部分，图象过点A（﹣3，0），对称轴为直线x=﹣1，给出四个结论，其中正确结论是九年级数学9-1
九年级数学9-2
（ ）
A．b2＜4ac
B．2a+b=0
C．a+b+c＞0
D．若点B（，y1）、C（，y2）为函数图象上的两点，则y1＜y2
6．下列命题中是真命题的为
A．长度相等的两条弧是等弧 B．平分弦的直径垂直于弦
C．圆的两条平行弦所夹的弧相等 D．相等的圆周角所对的弧相等
①
②
③
④
图1 图2
7．图1和图2中所有的小正方形都全等，将图1的正方形放在图2中①②③④的某一位置，使它与原来7个小正方形组成的图形是中心对称图形，这个位置是( )
A. ①
B. ②
C. ③
D. ④
8. 半径为 的圆的内接正六边形的边心距是（ ）
A．B．C．D．
9.如图，中，，，点B的坐标为（8，0），将绕点A逆时针旋转得到△CAD，当点O的对应点C落在OB上时，点D的坐标为（ ）
A．B．
C．D．
10．如图所示，点A，B，C均在6×6的正方形网格格点上，B，C三点的外接圆除经过A，B，C三点外还能经过的格点数为（ ）
A．4
B．5
C．6
D．7
二、填空题。（每小题3分，共15分）
11.已知x＝2是一元二次方程x2﹣mx+2＝0的一个根，则另一个根是
12. 抛物线中，无论m取何值都通过定点，则这个定点的坐标为 ．
13. 若 ，则的值为________
第14题图 第15题图
14．如图，在△ABC中，∠ACB＝90°，BC＝2．∠A=60°将△ABC绕点C逆时针旋转α角后得到△A′B′C，当点A的对应点A'落在AB边上时，阴影部分的面积为
15. 在平面直角坐标系中，点P（2，m）绕坐标原点O逆时针旋转 900后，恰好落在图中阴影区域（包括边界）内，则m的取值范围是________．
三、解答题。（共75分）
16．（8分）解方程：
（1）2x2﹣7x+3=0 （2）x（x﹣2）=x．
九年级数学9-3
九年级数学9-4
17．（9分）如图，A(0,1)，B(3,3)，C(1,3)，B1(-2,4)，C1(-2,2)
(1)△ABC绕点______逆时针旋转______度得到△AB1C1；
(2)画出△ABC绕原点O顺时针旋转90°的△A2B2C2，点C2坐标_______；若△ABC内一点P(m,n)在△A2B2C2的对应点为Q，则Q的坐标为______.（用含m，n的式子表示）
(3)在x轴上描出点M，使AM+BM最小，此时AM+BM=______.
18．（9分）关于x的一元二次方程x2+2x+k+1=0的实数解是x1和x2．
（1）求k的取值范围；
（2）如果x1+x2﹣x1x2＜﹣1且k为整数，求k的值．
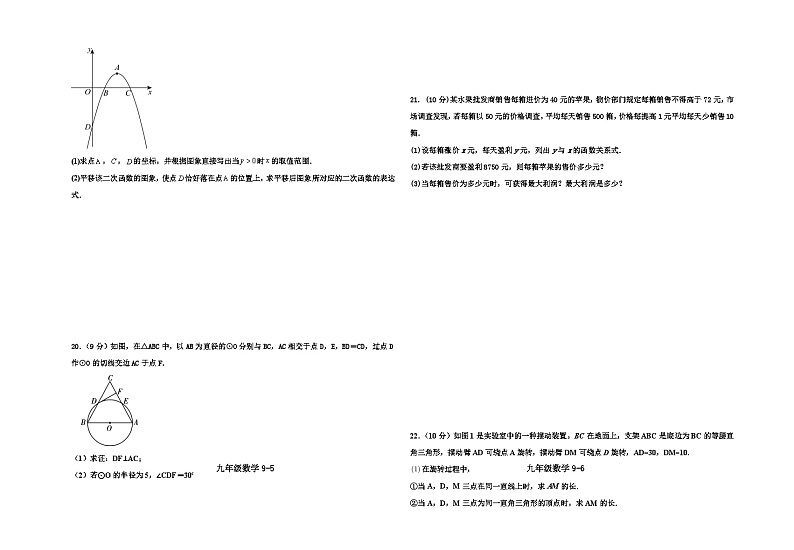
19.（9分）如图，在平面直角坐标系中，二次函数图象的顶点是，与轴交于，两点，与y轴交于点．点的坐标是(1,0)．

(1)求点，，的坐标，并根据图象直接写出当时的取值范围．
(2)平移该二次函数的图象，使点恰好落在点的位置上，求平移后图象所对应的二次函数的表达式．
20．（9分）如图，在△ABC中，以AB为直径的⊙O分别与BC，AC相交于点D，E，BD＝CD，过点D作⊙O的切线交边AC于点F.
九年级数学9-5
九年级数学9-6
（1）求证：DF⊥AC；
（2）若⊙O的半径为5，∠CDF＝30°，求弧BD的长(结果保留π)．
21. (10分)某水果批发商销售每箱进价为40元的苹果，物价部门规定每箱销售不得高于72元，市场调查发现，若每箱以50元的价格调查，平均每天销售500箱，价格每提高1元平均每天少销售10箱．
(1)设每箱涨价x元，每天盈利y元，列出y与x的函数关系式．
(2)若该批发商要盈利8750元，则每箱苹果的售价多少元？
(3)当每箱售价为多少元时，可获得最大利润？最大利润是多少？
22．（10分）如图1是实验室中的一种摆动装置，BC在地面上，支架ABC是底边为BC的等腰直角三角形，摆动臂AD可绕点A旋转，摆动臂DM可绕点D旋转，AD=30，DM=10.
在旋转过程中，
①当A，D，M三点在同一直线上时，求AM的长．
②当A，D，M三点为同一直角三角形的顶点时，求AM的长．
若摆动臂AD顺时针旋转90°，点D的位置由△ABC外的点D1转到其内的点D2处，连结D1D2，如图2，此时∠AD2C=135°，CD2=60，求BD2的长．
九年级数学9-7
九年级数学9-8
23.（11分）正方形和正方形的边长分别为6和2，将正方形绕点A逆时针旋转．
(1)当旋转至图1位置时，连接，，线段和有何关系？请说明理由；
(2)在旋转过程中，当点G，E，D在同一直线上时，请求出线段的长．
(3)在图1中，连接，，，请直接写出在旋转过程中：△BDF的面积最大值；
九年级数学答案
一．选择题：1--10 DDDAD CCCAB
二．填空题： 11、1 12、(3,17) 13、2 14、 15、-3≤x≤-2.5
三．解答题：
16. 解：（1）2x2﹣7x+3=0
……………………4分
解得：
（2）x（x﹣2）=x
x（x﹣3）=0，
解得：x1=0，x2=3．……………………8分
17.解：解
(1)A；90；……………………2分
如图所示，即为所求……………4分，
，，……………6分
如图所示，点M即为所求，……………7分
，……………9分
18．解：（1）∵方程有实数根，
∴△=22﹣4（k+1）≥0，
解得k≤0．
故K的取值范围是k≤0．…………4分
（2）根据一元二次方程根与系数的关系，得x1+x2=﹣2，x1x2=k+1，
x1+x2﹣x1x2=﹣2﹣（k+1）．
由已知，得﹣2﹣（k+1）＜﹣1，解得k＞﹣2．
又由（1）k≤0，
∴﹣2＜k≤0．
∵k为整数，
∴k的值为﹣1或0．…………9分
19.（1）解：把代入，得，解得：，…………1分
∴，
∴，…………2分
由得，当时，，
∴，…………3分
∵抛物线的对称轴是直线，两点关于直线对称，
∴，…………4分
∴根据图象可知：当时，；…………6分
（2）解：由（）知：，，
∴点平移到点，抛物线应向右平移个单位，再向上平移个单位，
∴平移后抛物线的解析式为．…………9分
20. （1）证明：连接OD，如图所示．…………1分
∵DF是⊙O的切线，D为切点，
∴OD⊥DF，
∴∠ODF=90°
∵BD=CD，OA=OB，
∴OD是△ABC的中位线，
∴OD∥AC，
∴∠CFD=∠ODF=90°，
∴DF⊥AC．…………5分
（2）解：∵∠CDF=30°，
由（1）得∠ODF=90°，
∴∠ODB=180°-∠CDF-∠ODF=60°
∵OB=OD，
∴△OBD是等边三角形，
∴∠BOD=60°，
∴BD弧的长= …………9分
21. （1）解：由题意得：，
化简得：，…………………3分
（2）解：依题意，把代入，
则，
∴，
则
则（故舍去），，
∴则每箱苹果的售价65元；…………………6分
（3）解：由（1）得出，
∴，
∵，
∴开口向下，在时，有最大值，且为，
则（元），
∴当每箱售价为70元时，可获得最大利润，最大利润是9000元．……………………10分
22.解：①，或…………2分
②显然不能为直角．
当为直角时，，
或舍弃
当时，，
或舍弃
综上所述，满足条件的AM的值为或…………6分
如图2中，连接
由题意：，，
，，
，
，
，
，
，
，
，，
≌，

所以 …………………………………10分
23. （1）结论：，，……………1分
理由如下：
如图1中，设交于点，交于点，
四边形，四边形都是正方形，
，，，
，
在和中，
，
∴，
，，
，
，
；……………4分
（2）解：如图中，当，，共线时，连接交于．
四边形是正方形，
，
，
，
，……………6分
如图中，当，，共线时，连接交于．
同法可得，可得，
综上所述，满足条件的的长为或；……………8分
（3）解：如图1中，连接，，，，，交于点，连接，过作交于，则，
四边形，四边形都是正方形，
，，，，
，，
，
，当，，三点共线时最大，
此时由，即，此时与重合，最大，
∵
∴当时最大，最大值为．……………11分