2023-2024学年高二数学下学期期末考试模拟04

这是一份2023-2024学年高二数学下学期期末考试模拟04，文件包含2023-2024学年高二数学下学期期末考试模拟04教师版docx、2023-2024学年高二数学下学期期末考试模拟04学生版docx等2份试卷配套教学资源，其中试卷共17页， 欢迎下载使用。
1. 5位同学报名参加两个课外活动小组，每位同学限报其中的一个小组，则不同报名方法有（ ）
A. 10种B. 20种C. 25种D. 32种
【答案】D
【解析】
【分析】由分步乘法原理计算．
【详解】由题意，每个同学有2种选择，故不同报名方式为.
故选：D
2. 设曲线y=ax-ln(x+1)在点(0,0)处的切线方程为y=2x，则a=
A. 0B. 1C. 2D. 3
【答案】D
【解析】
【详解】D
试题分析：根据导数的几何意义，即f′（x0）表示曲线f（x）在x=x0处的切线斜率，再代入计算．
解：，
∴y′（0）=a﹣1=2，
∴a=3．
故答案选D．
考点：利用导数研究曲线上某点切线方程．
3. 随机变量服从正态分布，且，则等于（ ）
A. 0.4B. 0.3C. 0.2D. 0.1
【答案】C
【解析】
【分析】根据给定条件，利用正态分布的对称性列式计算即得.
【详解】随机变量服从正态分布，且，
所以
故选：C
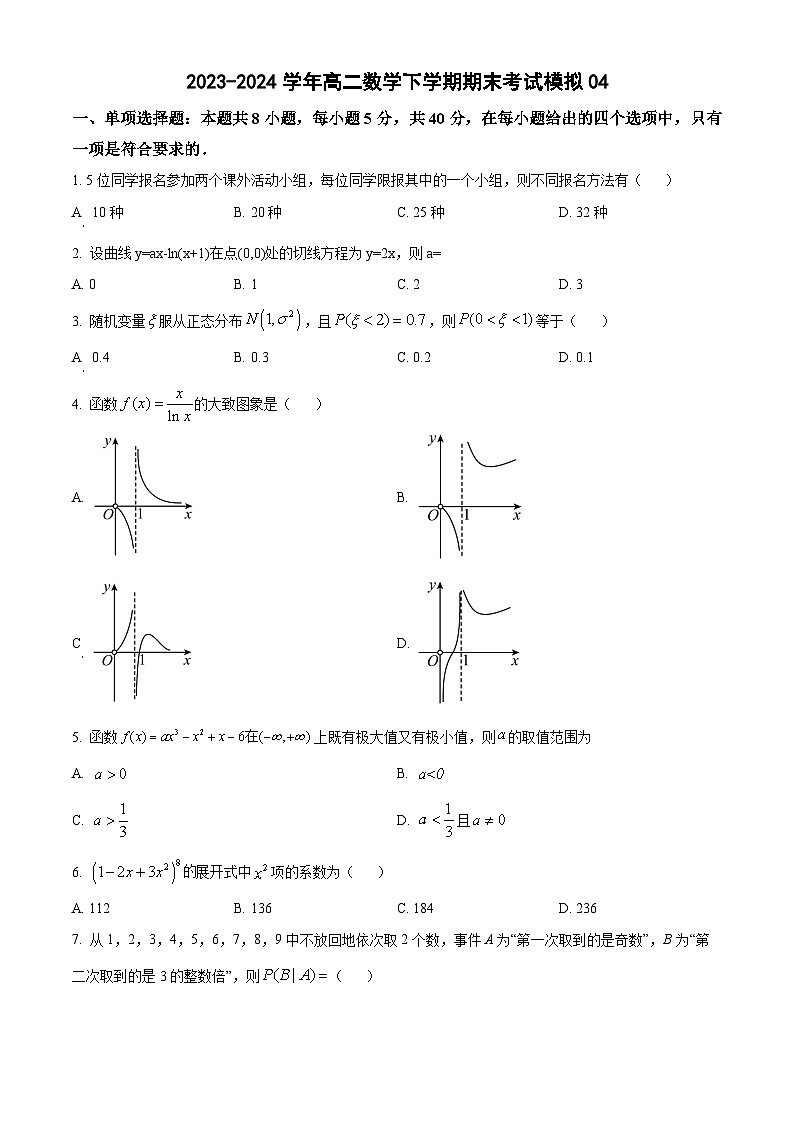
4. 函数的大致图象是（ ）
A. B.
C. D.
【答案】B
【解析】
【分析】利用排除法，先由函数的取值情况判断，再由导数判断函数的极值即可得答案
【详解】因为，
所以当时，，
可知C，D选项错误；
又，
当时，.
当时，，
故当时，取得极小值，故选项B正确.
故选：B.
5. 函数上既有极大值又有极小值，则的取值范围为
A. B.
C. D. 且
【答案】D
【解析】
【分析】根据上既有极大值又有极小值，得到至少有2个零点，列出不等式，求出且.
【详解】由题意得：至少有2个零点，
，解得：且，经验证，此时符合题意，
故选：D
6. 的展开式中项的系数为（ ）
A. 112B. 136C. 184D. 236
【答案】B
【解析】
【分析】根据题意，由二项式展开式的通项公式可知，或，再结合的展开式的通项公式代入计算，即可得到结果.
【详解】的展开式的通项为，
要得到项，必有，所以，所以，或.
当时，，而展开式中的项为，
故中项的系数为；
当时，，而中的常数项为1，
故中项的系数为，所以所求项的系数为.
故选：B.
7. 从1，2，3，4，5，6，7，8，9中不放回地依次取2个数，事件A为“第一次取到的是奇数”，B为“第二次取到的是3的整数倍”，则（ ）
A. B. C. D.
【答案】B
【解析】
【分析】由条件概率的定义，分别计算即得解.
【详解】由题意
事件为“第一次取到的是奇数且第二次取到的是3的整数倍”：若第一次取到的为3或9，第二次有2种情况；若第一次取到的为1，5，7，第二次有3种情况，故共有个事件
由条件概率的定义：
故选：B
【点睛】本题考查了条件概率的计算，考查了学生概念理解，分类讨论，数学运算的能力，属于中档题.
8. 设某公路上经过汽车不是货车就是客车，且货车与客车的数量之比为2∶1，货车中途停车修理的概率为0.02，客车为0.01，今有一辆汽车中途停车修理，则该汽车是货车的概率（ ）
A. 0.6B. 0.7C. 0.8D. 0.9
【答案】C
【解析】
【分析】先用全概率公式计算中途有车修理的概率，再用贝叶斯公式求这个条件概率即可.
【详解】设表示该汽车是货车，表示该汽车是客车，则
设表示货车中途停车修理，表示客车中途停车修理，表示汽车中途停车修理，
则
由全概率公式得
∴今有一辆汽车中途停车修理，该汽车是货车概率为:
故选：C.
二、多项选择题：本题共3小题，每小题6分，共18分，在每小题给出的选项中，有多项符合题目要求，全部选对的得6分，部分选对的得3分，有选错的得0分．
9. 已知随机变量，若，则，分别为（ ）
A. B. C. D.
【答案】BC
【解析】
【分析】由随机变量，得到，再利用期望和方差公式求解.
【详解】解：因为随机变量，
所以，
所以，
，
故选：BC
10. 下列命题中正确的为（ ）
A. 随机变量，若，，则
B. 若将一组数据中的每个数据扩大为原来的2倍，则方差也扩大为原来的2倍
C. 随机变量，若，则
D. 某人在10次射击中，击中目标的次数为X，，则当时概率最大
【答案】ACD
【解析】
【分析】根据二项分布的计算公式判断即可判断A；利用方差的性质即可判断B；利用正态分布的对称性求值即可判断C；利用二项分布的概率公式计算即可判断D．
【详解】对于A，因为，且，，所以，选项A正确；
对于B，若将一组数据中的每个数据都扩大为原来的2倍，则方差随之扩大为原来的4倍，选项B错误；
对于C，因为，且，
所以，选项C正确；
对于D，因为，
所以，，
令，解得，
因为，所以，即时，概率最大，选项D正确．
故选：ACD．
11. 若3男3女排成一排，则下列说法错误的是（ ）
A. 共计有720种不同的排法B. 男生甲排在两端的共有120种排法
C. 男生甲、乙相邻的排法总数为120种D. 男女生相间排法总数为72种
【答案】BC
【解析】
【分析】利用全排列、捆绑法、插空法对四种情况进行排列即可解得.
【详解】3男3女排成一排共计有种；男生甲排在两端的共有种；男生甲、乙相邻的排法总数种；男女生相间排法总数种；
故选：BC
【点睛】本题考查了全排列、捆绑法、插空法在排列组合中应用，属于简单题，解题时需要准确选择合理的方法是解题的关键.
三、填空题：本题共3小题，每小题5分，共15分．
12. 已知展开式的二项式系数之和为128，则展开式的第5项的系数是___________.
【答案】35
【解析】
【分析】由展开式的二项式系数之和为128，可求得n的值，继而求得展开式的第5项的系数.
【详解】由展开式的二项式系数之和为128，
可得 ，
故展开式的第5项的系数为 ,
故答案为：35
13. 等比数列{an}的前n项和为Sn，若S3+3S2=0，则公比q=_______
【答案】
【解析】
【详解】显然公比，设首项为，则由，得，即，即，即，所以，解得.
14. 法国数学家拉格朗日1797年在著作《解析函数论》中给出一个定理：如果函数满足条件：
（1）在闭区间是连续不断的；（2）在区间上都有导数.
则在区间上至少存在一个实数，使得，其中称为“拉格朗日中值”．
函数在区间上的“拉格朗日中值”______．
【答案】
【解析】
【分析】先求导，然后根据“拉格朗日中值”定义得到等式，最后解方程即可.
【详解】因为，所以,
结合“拉格朗日中值”定义可得,
所以，又因为，所以,
故答案为:
四、解答题：（解答题需写出明确的解答和证明过程，15-18题每题满分15分，19题满分17分，共77分）
15. （1）某校选派4名干部到两个街道服务，每人只能去一个街道，每个街道至少1人，有多少种方法?（结果用数字表示）
（2）如图，某水果店门前用3根绳子挂了6串香蕉，从左往右的串数依次为1，2，3.到了晩上，水果店老板要收摊了，假设每次只取1串（挂在一列的只能先收下面的），则将这些香蕉都取完的不同取法种数?（结果用数字表示）

【答案】（1）14种；（2）60种.
【解析】
【分析】（1）把4名干部按分成两组，再分配到两个街道列式计算作答.
（2）根据给定条件，利用倍缩法列式计算作答.
【详解】（1）依题意，把4名干部按分成两组，有种分组方法，按分成两组，有种分组方法，
所以4名干部按要求分到两个街道的不同方法数是（种）.
（2）依题意，6串香蕉任意收取有种方法，其中中间一列按从下往上有1种，占，
最右一列按从下往上只有1种，占，
所以不同取法数是（种）.
16. 在二项的展开式中，前三项系数的绝对值成等差数列.
（1）求展开式中二项式系数最大项;
（2）求展开式中各项的系数和.
【答案】（1）;
（2）.
【解析】
【分析】（1）根据二项式系数的对称性和单调性可得出二项式系数最大的项；
（2）在二项式的展开式中，令，可得各项系数和.
【小问1详解】
解：展开式的通项为，.
由已知: 、、，成等差数列，
即，所以.
二项式的展开项共9项，故二项式系数最大的项为第项，即
；
【小问2详解】
)令，各项系数和为.
17. 某食品厂为了检查一条自动包装流水线的生产情况，随机抽取该流水线上40件产品称出它们的质量（单位：克）作为样本数据，质量的分组区间为，，…，．由此得到样本的频率分布直方图如图．
（1）根据频率分布直方图，求质量超过505克的产品数量；
（2）在上述抽取的40件产品中任取2件，设X为质量超过505克的产品数量，求X的份布列和数学期望；
（3）从流水线上任取2件产品，设Y为质量超过505克的产品数量，求Y的分布列和方差．
【答案】（1）12件；
（2）分布列见解析，数学期望为；
（3）分布列见解析，方差为.
【解析】
【分析】（1）根据频率分布直方图直接可计算产品数量；
（2）由已知可知该分布为超几何分布，进而可得分布列与期望；
（3）由已知可知该分布为二项分布，进而可得分布列及方差.
【小问1详解】
质量超过克的产品的频率为，
所以质量超过克的产品数量为（件）.
【小问2详解】
质量超过克的产品数量为，
则质量未超过克的产品数量为，的取值为，，，
，，，
所以的分布列为
数学期望为.
【小问3详解】
根据用样本估计总体的思想，取一件产品，该产品的质量超过克的概率为，
从流水线上任取件产品互不影响，
因此质量超过克的件数可能的取值为，，，且，
，，，
所以的分布列为
方差为.
18. 已知数列的前项和，数列满足.
（1）求数列的通项公式；
（2）若，求数列的前项和.
【答案】（1）
（2）
【解析】
【分析】（1）由，可得，后可得的通项公式；
（2）由（1）可得，后可由错位相减法求数列的前项和.
【小问1详解】
当时，，
当时，，
又满足上式，∴，
∴.
【小问2详解】
由（1）得，，，∴，
∴，
∴，①
①×2得，②
①②得，
∴.
19. 已知
（1）当时，求在处切线方程；
（2）若在恒成立，求的取值范围；
（3）求证：．
【答案】（1）；
（2）；
（3）证明见解析.
【解析】
【分析】（1）把代入，求出函数的导数，利用导数的几何意义求出切线方程.
（2）将不等式等价变形成，按及讨论，构造函数借助单调性质可得，再分离参数即可求出的范围.
（3）由（2）的结论，当时成立，变形整理得，取，借助裂项相消法求和即可得证.
【小问1详解】
当时，，求导得，则，而，
所以在处切线方程为，即.
小问2详解】
，
当时，，当时，，则不等式恒成立，
此时，
当时，令函数，求导得，
函数在上单调递增，不等式，即，因此，
从而，令，
求导得，函数在上单调递增，，
则，所以的取值范围是.
【小问3详解】
由（2）知，当时，不等式对恒成立，
取，得，即，
因此，即，
则
，
所以原不等式成立.
【点睛】结论点睛：函数y=f(x)是区间D上的可导函数，则曲线y=f(x)在点处的切线方程为：.