黑龙江省佳木斯市桦南县第一中学2024-2025学年高二上学期期中考试数学试题

这是一份黑龙江省佳木斯市桦南县第一中学2024-2025学年高二上学期期中考试数学试题，共13页。试卷主要包含了单项选择题，多顶选择题，填空题，解答题等内容，欢迎下载使用。
第Ⅰ卷（选择题，共58分）
一、单项选择题：（本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一顶是符合题目要求.）
1.已知，，则的取值范围是（ ）
A.B.C.D.
2.已知复数满足，则的虚部为（ ）
A.－1B.－iC.3D.3i
3.已知，是两条不同的直线，，是两个不重合的平面，则下列命题中正确的是（ ）
A.若，，则B.若，，，则
C.若，，，则D.若，，则
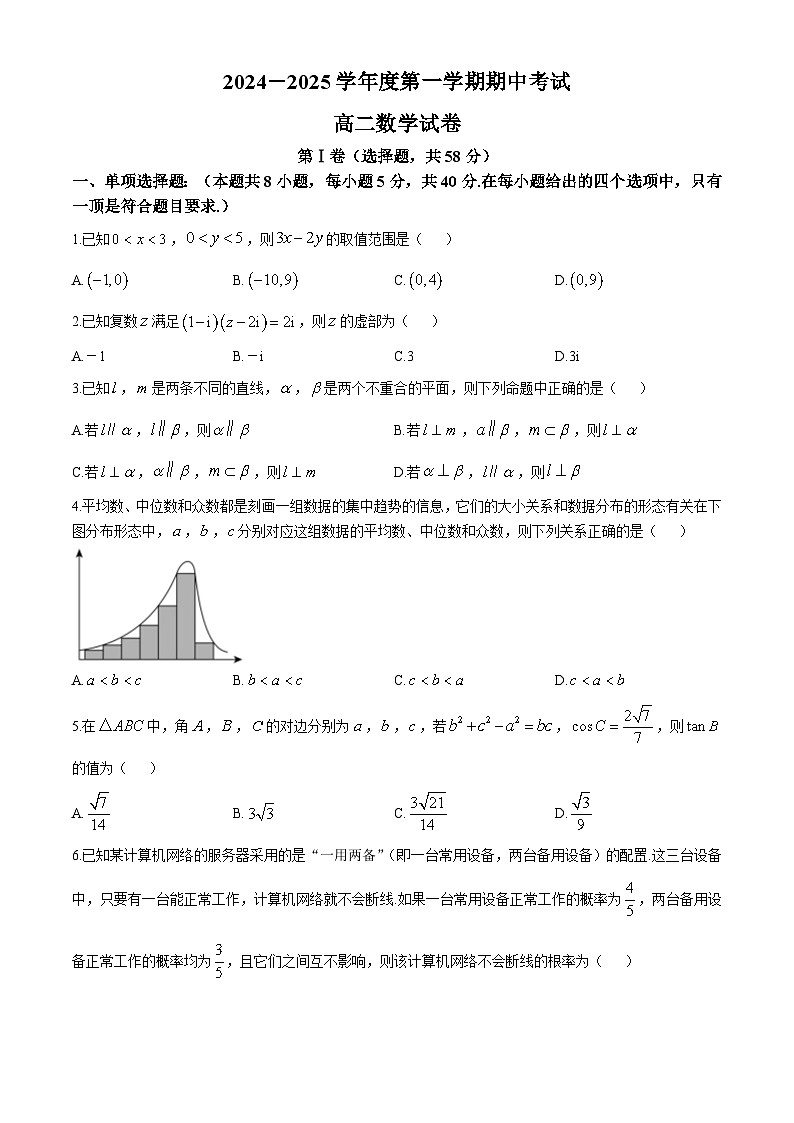
4.平均数、中位数和众数都是刻画一组数据的集中趋势的信息，它们的大小关系和数据分布的形态有关在下图分布形态中，，，分别对应这组数据的平均数、中位数和众数，则下列关系正确的是（ ）
A.B.C.D.
5.在中，角，，的对边分别为，，，若，，则的值为（ ）
A.B.C.D.
6.已知某计算机网络的服务器采用的是“一用两备”（即一台常用设备，两台备用设备）的配置.这三台设备中，只要有一台能正常工作，计算机网络就不会断线.如果一台常用设备正常工作的概率为，两台备用设备正常工作的概率均为，且它们之间互不影响，则该计算机网络不会断线的根率为（ ）
A.B.C.D.
7.已知定义在上的偶函数满足：①对任意的，，且，都有成立；②.则不等式的解集为（ ）
A.B.C.D.
8.设，过定点的动直线和过定点的动直线交于点，则的最大值是（ ）
A.5B.10C.D.
二、多顶选择题：（本题共3小题，每小题6分，共18分.在每小题给出的选项中，有多项符合题目要求.全部选对的得6分，部分选对的得部分分，有选错的得0分.）
9.将一枚质地均匀的骰子拋掷一次，记下骰子面朝上的点数，设事件“点数为4”，事件“点数为奇数”，事件“点数小于4”，事件“点数大于3”，则（ ）
A.与互斥B.A与互斥C.与对立D.与对立
10.已知圆和圆，则（ ）
A.圆的半径为4
B.轴为圆与的公切线
C.圆与公共弦所在的直线方程为
D.圆与上共有6个点到直线的距离为1
11.如图，正四棱柱中，，，点，，分别为棱，，的中点，则下列结论中正确的有（ ）
A.B.平面
C.D.点到平面的距离为
第Ⅱ卷（共92分）
三、填空题：（本大题共3小题，每题5分，共计15分）
12.已知直线与直线垂直，则实数的值为________.
13.甲、乙两名运动员进入男子羽毛球单打决赛，假设比赛打满3局，赢得2局或3局者胜出，用计算机产生1~5之间的随机数，当出现随机数1，2，3时，表示一局比赛甲获胜；否则，乙获胜.由于要比赛3局，所以每3个随机数为一组，产生20组随机数：
423 123 423 344 114 453 525 332 152 342
534 443 512 541 125 432 334 151 314 354
据此估计甲获得冠军的概率为________.
14.在边长为的菱形ABCD中，，沿对角边折成二面角为的四面体，则四面体外接球表面积为________.
四、解答题：（本大题共5小题，共计77分）
15.（满分13分）如图，四面体中，，分别为，上的点，且，，设，，.
（1）以为基底表示；
（2）若，且，，，求.
16.（满分15分）已知两直线，，是和的交点.
（1）求过点A且垂直于直线的直线的方程.
（2）求过点A且平行于直线的直线的方程.
17（满分15分）已知集合，，.
（1）求为一次函数的概率；
（2）求为二次函数的概率.
18.（满分17分）已知圆，直线过点.
（1）若直线与圆相切，求直线的方程；
（2）若直线与圆相交于，两点，求三角形的面积的最大值，并求此时直线的方程.
19.（满分17分）如图，四棱锥中，平面，，，，为的中点，且.
（1）求证：平面平面；
（2）求二面角的余弦值.
参考答案：
1.B
【分析】由不等式的性质求解.
【详解】因为，所以，又，所以
所以.
故选：B.
2.C
【分析】利用复数定义及运算法则计算即可.
【详解】因为，所以的虚部为3，
故选：C.
3.C
【解析】采用逐一验证法，结合线线关系、线面关系、面面关系可得结果.
【详解】对A，，，与不一定平行，也可能相交，故A错
对B，一条线要垂直平面内的两条相交直线才会得到线面垂直，故不会垂直，由于，所以也不会垂直，故B错
对C，由，，所以，又，则，故C正确
对D，，，与可以相交，也可以在平面内，故D错
故选：C
【点睛】本题考查线线关系、线面关系、面面关系，审清题意，熟记线面垂直、平行的判定定理以及性质定理，属基础题.
4.A
【分析】利用数据分布图左拖尾，即平均数小于中位数，再利用众数是用最高矩形的中点值来估计，可判断众数大于中位数，即可作出判断.
【详解】由数据分布图知，众数是最高矩形下底边的中点横坐标，因此众数为右起第二个矩形下底边的中点值，
直线左右两边矩形面积相等，而直线左边矩形面积大于右边矩形面积，则，又数据分布图左拖尾，则平均数小于中位数，即，
所以.
故选：A
5.B
【分析】由已知利用余弦定理可求A，然后结合同角基本关系可求，再由诱导公式及两角和的正切公式即可求解.
【详解】解：因为，
由余弦定理得，，
由A为三角形内角得，，
因为，则为锐角，，
所以，，
则.
故选：B.
6.A
【分析】利用其对立事件三台设备均不能正常工作计算.
【详解】由题意所求概率为.
故选：A.
7.A
【分析】由题意得，偶函数在上单调递增，在上单调递减，作出函数的大致图像，利用数形结合即可得解.
【详解】由题意得，偶函数在上单调递增，在上单调递减，且，作出函数的大致图像如下：
不等式等价于或，
数形结合可知不等式的解集为：
故选：A.
8.A
【分析】根据直线方程确定定点坐标，再根据直线垂直的判定可得两直线相互垂直，结合勾股定理、基本不等式有，注意等号成立条件，即可求最大值.
【详解】由题设知：，，又，故两条动直线相互垂直，
所以，即，当且仅当时等号成立.
故选：A.
9.ABD
【分析】利用互斥事件和对立事件的概念求解.
【详解】事件“点数为4”与“点数为奇数”不能同时发生，所以A与互斥，A正确.
事件“点数为4”与“点数小于4”不能同时发生，所以A与互斥；B正确.
事件“点数为奇数”的对立事件是“点数为偶数”，不是“点数大于3”，C错误.
事件“点数小于4”的对立事件是“点数不小于4”，即“点数大于3”，与对立，D正确.
故选：ABD.
10.BD
【分析】
对于A项，将圆的方程化成标准式即得；对于B项，判断圆心到直线的距离等于圆的半径即得；对于C项，只需将两圆方程相减化简，即得公共弦直线方程；对于D项，需要结合图像作出两条和已知直线平行且距离等于1的直线，通过观察分析即得.
【详解】
对于A项，由圆配方得：，知圆的半径为2，故选项A错误；
对于B项，因圆心到轴的距离为1，等于圆的半径，故圆与轴相切，同理圆心到轴的距离等于圆的半径，圆与轴相切，故轴为圆与的公切线，故选项B正确；
对于C项，只需要将与左右分别相减，即得圆与的公共弦所在的直线方程为：，故选项C错误；
对于D项，如图，因直线同时经过两圆的圆心，依题意可作两条与该直线平行且距离为1的直线与，其中与和圆都相切，各有一个公共点，与和圆都相交，各有两个交点，故圆与上共有6个点到直线的距离为1，故选项D正确.
故选：BD.
11.ABD
【分析】以为原点，分别以、、所在直线为、、轴建立空间直角坐标系，求出、的坐标，求数量积可判断A；求出、平面的一个法向量的坐标，由线面平行的向量求法可判断B；求出、的坐标，根据向量共线的条件可判断C；利用点到平面的距离的向量求法可判断D.
【详解】以为原点，分别以、、所在直线为、、轴建立如图所示的空间直角坐标系，则，，，，，，
对于A，，，所以，
即，所以，故A正确；
对于B，，，，，，，，，设为平面的一个法向量，
所以，即，令，则，所以，
所以，，所以平面，故B正确；
对于C，，，，，
，，所以，所以与不平行，故C错误；
对于D，平面的一个法向量为，，
所以点到平面的距离为，故D正确.
故选：ABD，
12.或
【分析】根据向量垂直列方程，由此求得的值
【详解】由于，所以，，解得或.
故答案为：或
【分析】根据题意找出甲获胜的情况，然后利用古典概型的概率公式求解.
【详解】由题意得甲获胜的情况有：423，123，423，114，332，152，342，512，125，432，334，151，314，共13种，
所以估计甲获得冠军的概率为.
故答案为：0.65
14.
15.（1） （2）
【分析】（1）利用向量的加减数乘运算，结合题设条件即可求得；
（2）先求出平面的基底两两之间的数量积，再根据（1）中的表示式，两边取平方，利用向量数量积的运算律计算即得.
【详解】（1）由图可得，；
（2）由题意，，，
则，
于是，由两边取平方，
，
故.
16.（1）；（2）.
【分析】（1）求出点，根据垂直斜率相乘为－1求出斜率，由点斜式求出方程；
（2）根据平行设直线为，代入点A求出方程.
【详解】（1）联立方程解得，
，且，
，
，
整理得：；
（2）令，
过，代入得：，
.
【点睛】本题考查直线与直线交点的求法，以及与已知直线平行、垂直的直线的求法，属于基础题.
17.（1）；（2）.
【分析】（1）根据一次函数的定义，结合古典概型公式进行求解即可；
（2）根据二次函数的定义，结合古典概型公式进行求解即可.
【详解】（1）样本空间有个结果，为一次函数，即，，共4种情况，所以概率为；
（2）样本空间有个结果，为二次函数，即，共20种情况，所以概率为.
18.（1）或；（2）答案见解析.
【详解】
（1）①若直线的斜率不存在，则直线，符合题意；
②若直线斜率存在，设直线的方程为，即，
由题意知，圆心到已知直线的距离等于半径2，
即，解得，
所求直线的方程是或；
（2）方法一：直线与圆相交，斜率必定存在，且不为0，设直线方程为，则圆心到直线的距离，
又三角形面积
，
当且仅当，即时取等号，三角形的面积的最大值为2，
由，有，或，
此时直线方程为，或.
方法二：，
当时，取最大值2，
此时点到的距离为，
设，
由，解得或，
故所求直线的方程为或.
19.（1）见解析 （2）
【分析】（1）先在面内证明，再证明面，，证得面，由面面垂直的判定定理得到平面平面.
（2）建系，利用法向量求二面角的平面角的余弦值.
【详解】（1）证明：平面，，平面
为的中点，，，
，，，，
，
，
又平面，平面，，
又，，，平面，
平面，又平面，
，又，，，平面，
平面，
平面，
所以平面平面.
（2）
在面内，过作，
平面，，，两两相互垂直，
以为坐标原点，，，所在直线分别为，，轴建立如图空间坐标系，
由（1）知，，为中点，则，
则，，，，，
，，，
面，面的一个法向量是，
设面的法向量，
则 ，
所以面的一个法向量为，
，
所以二面角的余弦值为.
题号
1
2
3
4
5
6
7
8
9
10
答案
B
C
C
A
B
A
A
A
ABD
BD
题号
11
答案
ABD