
广东省茂名市高州市2024-2025学年八年级上学期11月期中考试数学试题
展开
这是一份广东省茂名市高州市2024-2025学年八年级上学期11月期中考试数学试题,共5页。试卷主要包含了单选题,填空题,解答题等内容,欢迎下载使用。
(满分为120分,考试时间为120分钟)
一、单选题(每小题3分,共30分)
1.下列实数中,无理数是( )
A.2B.2C.3.14159D.722
2.满足下列条件时,△ABC不是直角三角形的是( )
A.B.
C.AB=6,BC=8,AC=10D.AB:BC:AC=5:12:13
3.根据下列表述,能确定具体位置的是( )
A.万达影城一号厅第三列B.高州市府前路
C.南偏西D.东经,北纬
4.在平面直角坐标系中,点P3,-2在( )
A.第一象限B.第二象限C.第三象限D.第四象限
5.下列各式正确的是( )
A.±9=±3B.--16=4C.1619=413D.38=±2
6.二次根式2-x有意义,则x的值可以为( )
A.4B.1C.3D.5
7.某数学兴趣小组开展了笔记本电脑的张角大小的实践探究活动.如图,当张角为∠DAF时,顶部边缘D处离桌面的高度DE为20cm,此时底部边缘A处与E处间的距离AE为15cm,小组成员调整张角的大小继续探究,最后发现当张角为∠BAF时(D是B的对应点),顶部边缘B处到桌面的距离BC为7cm,则底部边缘A处与C之间的距离AC为( )
A.13cmB.15cmC.20cmD.24cm
8.估算2+19的值应在( )
A.4到5之间 B.5到6之间 C.6到7之间 D.7到8之间
八年级数学 第1页,共6页 第2页,共6页 第3页,共6页
第7题图 第9题图
9.实数a、b在数轴上对应的点的位置如图所示,则化简a-b2-b2得( )
A.a B.-a C.a-2b D.2b-a
10.已知点A的坐标为(a﹣1,3+a),下列说法正确的是( )
A.若点A在y轴上,则a=﹣3 B.若点A在二四象限角平分线上,则a=1
C.若点A到x轴的距离是3,则a=0或﹣6 D.若点A在第四象限,则a的值可以为2
二、填空题(每小题3分,共15分)
11.实数-27的立方根是 .
12.若a+3+(b-4)2=0,则点M(a,b)关于x轴的对称点的坐标为 .
13.若一个正整数的两个平方根为2x-7与-x+1,则这个数是 .
14.在平面直角坐标系中,对△ABC进行循环往复的轴对称变换,若原来点的坐标是2,3,则经过第2024次变换后所得的点的坐标是 .
15.如图,在Rt△ABC中,∠ACB=90°,AC=5,BC=12,AD平分∠CAB交BC于D点,E,F分别是AD,AC上的动点,则CE+EF的最小值为 .
三、解答题(一)(本大题4小题,其中第16题8分,17-19每题6分,共26分)
16.计算:.(1) (2)1-2+12-1+612
17.已知2a+1=5,的平方根是±6,求a+4b的平方根.
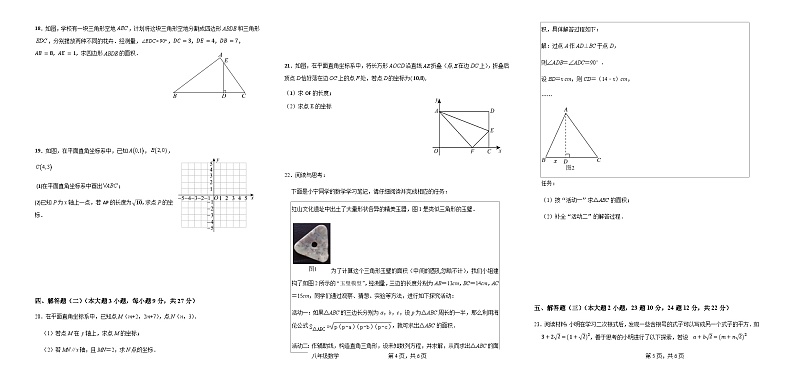
18.如图,学校有一块三角形空地,计划将这块三角形空地分割成四边形和三角形,分别摆放两种不同的花卉.经测量,,DC=3,DE=4,DB=7,AB=8,AE=1,求四边形的面积.
19.如图,在平面直角坐标系中,已知,,
(1)在平面直角坐标系中画出;
(2)已知P为x轴上一点,若AP的长度为10,求点P的坐标.
四、解答题(二)(本大题3小题,每小题9分,共27分)
20.在平面直角坐标系中,已知点M(m+2,2m+7),点N(n,3).
(1)若点M在 y轴上,求点M的坐标;
(2)若MN∥x轴,且MN=2,求N点的坐标.
21.如图,在平面直角坐标系中,将长方形沿直线折叠(点在边上),折叠后顶点恰好落在边上的点处,若点的坐标为10,8,
(1)求OF的长度;
(2)求点E的坐标
22.阅读与思考:
八年级数学 第4页,共6页 第5页,共6页 第6页,共6页
下面是小宁同学的数学学习笔记,请仔细阅读并完成相应的任务:
任务:
(1)按“活动一”求△ABC的面积;
(2)补全“活动二”的解答过程.
五、解答题(三)(本大题2小题,23题10分,24题12分,共22分)
23.阅读材料:小明在学习二次根式后,发现一些含根号的式子可以写成另一个式子的平方.如3+22=1+22,善于思考的小明进行了以下探索,若设 a+b2=m+n22
=m2+2mn2+2n2(其中,a,b,m,n均为整数),则有a=m2+2n2,b=2mn,这样小明就找到一种把类似a+b的式子化为平方式的方法.请你依照小明的方法探索并解决下列问题:
(1)若a+b3=m+n32,当a,b,m,n均为整数时,用含m,n的式子分别表示a,b,得:a= ,b= .
(2)若a+47=m+n72,当a,m,n均为正整数时,求a的值.
(3)化简:9-45.
24.△ABC中,为△ABC外一点.
【探究发现】
(1)如图1,点D在边下方,.学校的数学兴趣小组的同学们尝试探究此时线段之间的数量关系.他们的思路是这样的,作,取,连接BE.易证△ADC≌△BEC.通过等量代换得到线段之间的数量关系.请根据同学们的思路, 写出△ADC≌△BEC的证明过程.
【迁移运用】
(2)如图2,点D在边上方,.猜想线段AD、BD、CD之间的数量关系,并证明你的结论.
【延伸拓展】
(3)图3,在四边形中,,若AD=3,CD=6,请直接写出的值.
红山文化遗址中出土了大量形状各异的精美玉器,图1是类似三角形的玉璧.
为了计算这个三角形玉璧的面积(中间的圆孔忽略不计),我们小组建构了如图2所示的“玉璧模型”,经测量,三边的长度分别为AB=13cm,BC=14cm,AC=15cm,同学们通过观察、猜想、实验等方法,进行如下探究活动:
活动一:如果△ABC的三边长分别为a,b,c,设p为△ABC周长的一半,那么利用海伦公式,就可求出△ABC的面积.
活动二:作辅助线,构造直角三角形,设未知数列方程,并求解,从而求出△ABC的面积,具体解答过程如下:
解:过点A作AD⊥BC于点D,
则∠ADB=∠ADC=90°,
设BD=x cm,则CD=(14﹣x)cm,
……
2024-2025学年度第一学期学情练习(第10周)
八年级数学参考答案
一选择题
1、B 2、B 3、D 4、D 5、A 6、B 7、D 8、C 9、B 10、C
二填空题
11、-3 ,12、(-3,-4), 13、25 , 14、(-2,3), 15、6013
三解答题
16(1) 解:原式=33﹣23﹣2 ………………………..3分
=3-2……………………….4分
(2)原式=2-1+2+6×22…………………….6分
=2+1+32…………………….7分
=42+1…………………….8分
17.解;依题意得2a+1=25 3a+b-1=36 …………………….2分
∴a=12 b=1 …………………….4分
∴a+4b=12+4×1=16,……………………5分
∴a+4b的平方根为±4…………………….6分
18解:∵,
∴CE=CD2+DE2=32+42=5,…………………….1分
∵AE=1,
∴AC=AE+CE=6,BC=BD+CD=3+7=10,…………………….2分
∵AB=8,AB2+AC2=100=BC2,…………………….4分
∴,
∴SABDE=S△ABC-S△DEC=12×6×8-12×3×4=36…………………….6分
19(1)解:如下图所示.…………………….3分
(2)∵P为x轴上一点,AB=10 ,∠AOP=90°AO=1
∴OP=3…………………….5分
∴点P的坐标为:(3,0)或(-3,0)…………………….6分
20(1)∵点M(m+2,2m+7)在y轴上,
∴m+2=0,……………………1分
解得: m=﹣2.…………………….2分
∴2m+7=3 …………………….3分
∴M点坐标为(0,3)……………………4分
(2)∵MN∥x轴,且MN=2,点M(m+2,2m+7),点N(n,3),
∴2m+7=3,…………………….5分
解得m=-2,…………………….6分
∴M(0,3) ……………………7分
因为MN=2∴N点为(2,3)或(-2,3)…………………….9分
21. (1)∵长方形沿直线折叠(点在边上)
∴AD=AF =OC AO=DC…………………….1分
∵的坐标为10,8
∴AD=AF =OC=10 AO=DC=8…………………….2分
在直角三角形AOF中OF=6…………………….4分
(2)由(1)可知 OC=10 ,OF=6
∴FC=4…………………….5分
设EC=x,则DE=8-x,
∵折叠∴EF=DE=8-x, …………………….6分
在直角三角形ECF中42+x2=(8-x)2…………………….7分
解得x=3…………………….8分
∴E点坐标为(10,3)…………………….9分
22、解:(1)∵AB=13(厘米),BC=14(厘米),AC=15(厘米),
∴(厘米),……………………2分
∴…………………….4分(平方厘米);
(2)过点A作AD⊥BC于点D,
设BD=x厘米,则CD=(14﹣x)厘米,
∴∠ADB=∠ADC=90°,
根据勾股定理得:AD2=AB2﹣BD2=AC2﹣CD2,
即132﹣x2=152﹣(14﹣x)2,……………………5分
解得:x=5,…………………….7分
∴(厘米),…………………….8分
∴(平方厘米).……………………9分
23 、解:(1)
∴a=m2+3n2,b=2mn,…………………….2分
(2)∵a+4a+47=m+n72=m+n72,
∴ a+47==m2+2nm7+7n2(a,b,m,n均为整数),…………………….3分
∴a=m2+7n2,2mn=4,…………………….4分
∴mn=2, …………………….5分
m=1,n=2,a=29,…………………….6分
m=2,n=1,a=11,
综上所述:a=29或11;…………………….7分
(3)∵2-52=4-45+5=9-45…………………….8分
∴9-45=2-52=2-5=5-2…………………….10分
24、证明:(1)作,取,连接.
∵,…………………….1分
∴,
∵,,,……………………3分
∴.…………………….4分
(2)解:AD=BD+2CD,证明如下.
在上截取,使,
∵,
∴,……………………5分
∴,
∵,,,
∴,…………………….6分
∴,
∵∠ACB=∠CAE+∠ECB=90°,
∴∠BCD+∠ECB=∠CAE+∠ECB=90°,
∴∠ECD=90°, ………………….7分
∵EC=CD
∴CE2+CD2=ED2,∴2CD2=ED2
∴ED=2CD………………….8分
∵AD=AE+ED,∴AD=BD+2CD………………….9分
(3)9
解:如图,过点C作,使,连接DE,,
∴DE=CD2+CE2=62,
∵,
∴,
∴,即,
在和中,
,
∴,
∴.
∵,,
∴.
∴BD=AE=DE2+AD2=622+32=9………………….12分
相关试卷
这是一份广东省茂名市高州市2024-2025学年九年级上学期11月期中联考数学试题,文件包含24-25第一学期第11周联考九年级数学参考答案pdf、九年级数学pdf、九年级数学答题卡pdf等3份试卷配套教学资源,其中试卷共9页, 欢迎下载使用。
这是一份广东省茂名市高州市2023-2024学年八年级下学期期中数学试题,共17页。试卷主要包含了单选题,填空题,解答题等内容,欢迎下载使用。
这是一份广东省茂名市高州市2023-2024学年八年级下学期月考数学试题(含解析),共15页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。









