人教A版 (2019)必修 第一册2.3 二次函数与一元二次方程、不等式第1课时教案

这是一份人教A版 (2019)必修 第一册2.3 二次函数与一元二次方程、不等式第1课时教案，共8页。教案主要包含了教学目标，教学重难点，教学过程等内容，欢迎下载使用。
2.3二次函数与一元二次方程、不等式(一)

一、教学目标
1. 理解一元二次方程、一元二次不等式与二次函数的关系，掌握图象法解一元二次不等式的方法;
2. 经历从实际情境中抽象出一元二次不等式模型的过程和通过函数图象探究一元二次不等式与相应函数、方程的联系，获得一元二次不等式的解法;
3. 培养勇于探索的精神，勇于创新精神，同时体会事物之间普遍联系的辩证思想.
二、教学重难点
重点：从实际问题中抽象出一元二次不等式模型; 体会数学建模的过程与数形结合的思想.
难点：理解二次函数、一元二次方程与一元二次不等式的关系.

三、教学过程
(一) 创设情境
情境导入:
园艺师打算在绿地上用栅栏围一个矩形区域种植花卉.若栅栏的长度是24 m，围成的矩形区域的面积要大于20 m2，则这个矩形的边长为多少米？
设矩形的一边长为x m，则另一边长为(12－x) m，由题意，得
(12－x)x>20, 00； （2）9x2－6x＋1>0； （3）－x2+2x－3>0．
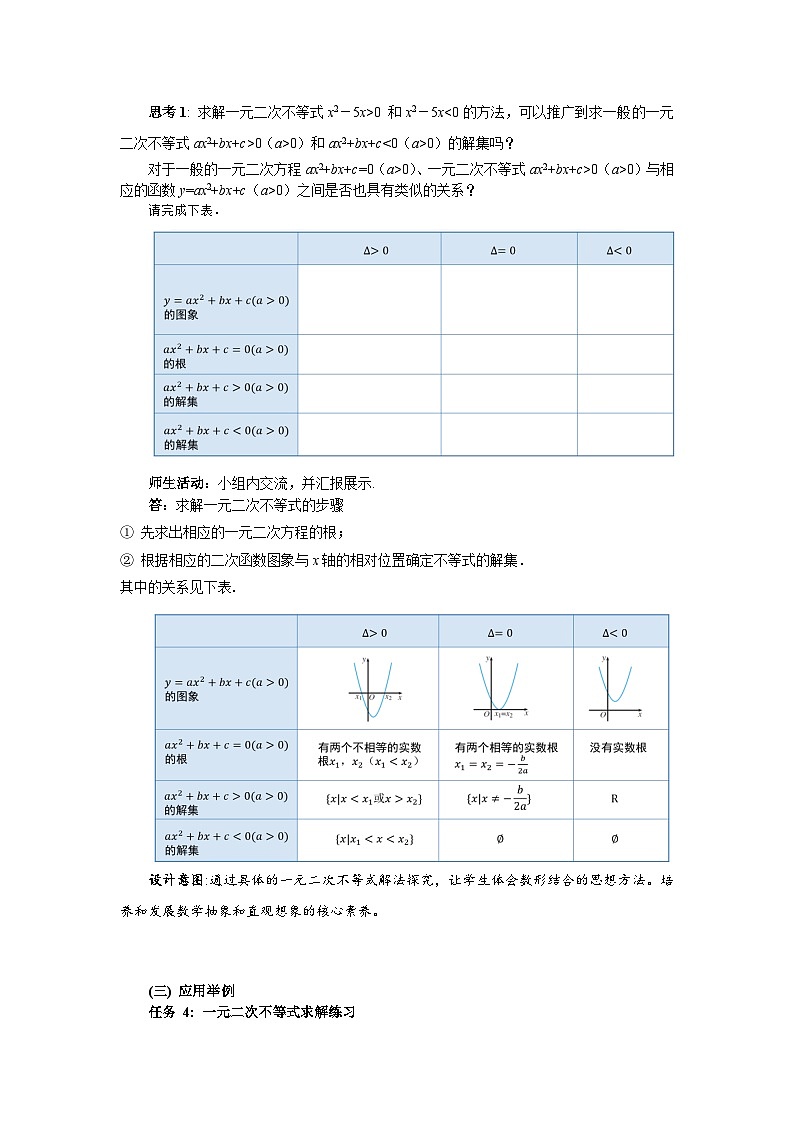
思考1 求解不等式ax2＋bx＋c>0或ax2＋bx＋c0)的依据是什么？步骤是什么？
答: 求解不等式ax2＋bx＋c>0或ax2＋bx＋c0)的依据是相应的函数图象与x轴的相对位置关系．步骤如下:
① 先求出相应的一元二次方程的根;
② 画出二次函数的图象;
③ 根据相应的二次函数图象与x轴的相对位置确定不等式的解集.
解: (1) 对于方程x2－5x＋6=0，因为>0，所以它有两个实数根，解得x1=2，x2=3． 画出二次函数y=x2－5x＋6的图象(如图 1), 结合图象得不等式x2－5x＋6>0的解集为{x|x3}．
图2
图1
(2) 对于方程9x2－6x＋1=0，因为Δ=0，所以它有两个相等的实数根，解得x1=x2=．画出二次函数y=9x2－6x＋1的图象(图2)．结合图象得不等式9x2－6x＋1>0的解集为xx≠13．
图4
(3) 法一: 不等式可化为x2－2x+3