山西省实验中学2024-2025学年九年级上学期11月期中数学试题

这是一份山西省实验中学2024-2025学年九年级上学期11月期中数学试题，文件包含山西省太原市杏花岭区山西省实验中学2024-2025学年九年级上学期11月期中数学试题docx、答案pdf等2份试卷配套教学资源，其中试卷共10页， 欢迎下载使用。

九年级 数 学
(本试卷满分100分，考试时间90分钟)
一、单项选择题(本题共10个小题，每小题3分，共30分)
1. 如图，该几何体的主视图是 ( )
2. 已知x=1是方程 2x²-3x+c=0的一个根，则c的值是( )
A. 1 B. 2 C. - 1 D. - 2
3. 如图, AB∥CD∥EF, 若 ACCE=43,BD=16, 则DF的长为( )
A. 6 B. 9 C. 12 D. 15
4. 在一个不透明的布袋中装有30个黄、白两种颜色的球，除颜色外其他都相同，小红通过多次摸球试验后发现，摸到黄球的频率稳定在0.4左右，则布袋中白球可能有( )
A. 12个 B. 15个 C. 18个 D. 20个
5. 泰勒斯是古希腊时期的思想家，科学家，哲学家，他最早提出了命题的证明. 泰勒斯曾通过测量同一时刻标杆的影长，标杆的高度，金字塔的影长，推算出金字塔的高度，这种测量原理，就是我们所学的( )
A. 图形的平移 B. 图形的旋转
C. 图形的轴对称 D. 图形的相似
6. 关于x的一元二次方程 x²-kx-1=0的根的情况是( )
A. 方程有两个不相等的实数根 B. 方程有两个相等的实数根
C. 方程没有实数根 D. 方程的根的情况与k的取值有关
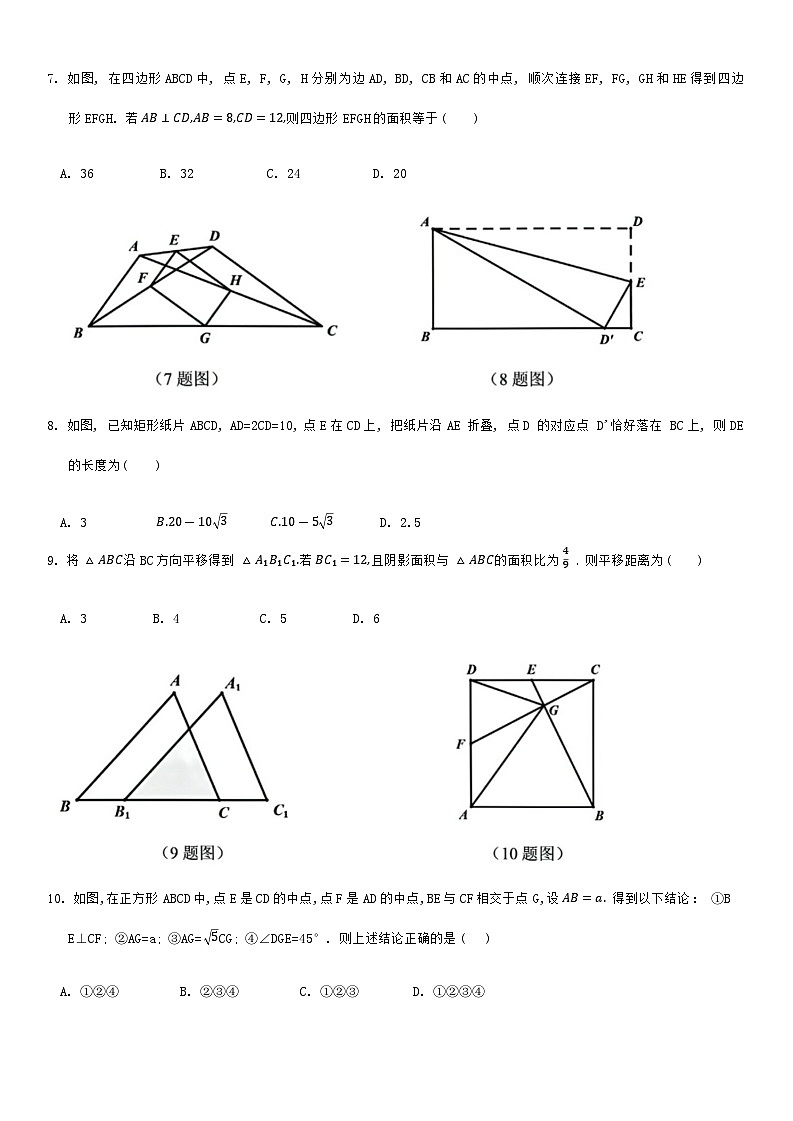
7. 如图, 在四边形ABCD中, 点E, F, G, H分别为边AD, BD, CB和AC的中点, 顺次连接EF, FG, GH和HE得到四边形EFGH. 若 AB⊥CD,AB=8,CD=12,则四边形EFGH的面积等于( )
A. 36 B. 32 C. 24 D. 20
8. 如图, 已知矩形纸片ABCD, AD=2CD=10, 点E在CD上, 把纸片沿AE 折叠, 点D 的对应点 D'恰好落在 BC上, 则DE的长度为( )
A. 3 B.20-103 C.10-53 D. 2.5
9. 将 △ABC沿BC方向平移得到 △A₁B₁C₁.若 BC₁=12,且阴影面积与 △ABC的面积比为 49 ，则平移距离为( )
A. 3 B. 4 C. 5 D. 6
10. 如图,在正方形ABCD中,点E是CD的中点,点F是AD的中点,BE与CF相交于点G,设 AB=a. 得到以下结论: ①BE⊥CF; ②AG=a; ③AG= 5CG; ④∠DGE=45°. 则上述结论正确的是( )
A. ①②④ B. ②③④ C. ①②③ D. ①②③④二、填空题(本题共5个小题，每小题3分，共15分)
11. 已知 ab=cd=23,且b+d≠0, 则 a+cb+d= .
12. 如图为太原古县城示意图，小君和小帆都从南门进入古县城游览，结束时分别从其余四个门中的一个离开，他们恰好从同一城门走出的概率是 .
13. 黄金分割大量应用于艺术、大自然中，树叶的叶脉也蕴含着黄金分割，如图，P为AB的黄金分割点(AP>PB),如果AB的长度为10cm,则BP的长度为 cm.
14. 用12m长的铁丝围成一个一边靠墙的长方形场地，使场地的面积为 15m²,并且在垂直于墙的一边开一个1m长的小门 (该门用其他材料)，若墙长足够长，设该长方形场地平行于墙的边长度为xm，则列方程为 .
15. 如图, 在菱形ABCD中, AC为对角线,. AE⊥BC于点E，点F是AE延长线上一点，且 ∠ABF=∠AFB, 线段AC， BF的延长线交于点 G.若菱形ABCD的面积为 165,AE=85,则CG的长为 .三、解答题(本题共8个小题，共55分)
16. (8分) 解方程:
1x²+2x-4=0; 23x+2²=xx+2.
17.(6分)如图，在路灯下，小华的身高用线段AB表示，他在地面上的影子用线段AC表示，小玉的身高用线段FG表示，路灯灯泡在线段 DE上.
(1) 请你确定灯泡所在的位置，并画出小玉在灯光下形成的影子；
(2)如果小华的身高AB=1.64m,他的影子长AC=1.4m,且他到路灯的距离AD=2.1m，则灯泡的高为 .
18. (6分)如图，△ABC在坐标平面内，三个顶点的坐标分别为A(3,0), B(4,2), C(2,4)(正方形网格中每个小正方形的边长为1).
(1) 以点O为位似中心，在第一象限画出△ABC的位似图形 △A₁B₁C₁, 使△A₁B₁C₁与△ABC的位似比为2: 1;
(2) 若点 P (a, b) 是△ABC 上的任意一点, 则变换后的对应点 P₁的坐标是 .
19.(6分)如图，已知矩形ABCD的对角线AC的垂直平分线与边AD、BC分别交于点E、F, 连接AF, CE.
(1) 求证: 四边形AFCE 是菱形;
(2)当 BC=3,AB=2时，则菱形AFCE的面积为 .20. (6分)数学选修课开展“讲数学家故事”的活动. 下面是印有四位中国数学家卡通图案的卡片A，B，C，D，卡片除图案外其他均相同. 将四张卡片背面朝上，洗匀后放在桌面上，同学们可以从中随机抽取卡片，讲述卡片上数学家的故事.
(1) 小哲随机抽取了一张卡片，卡片上是数学家刘徽卡通图案的概率是 ；
(2)小涵随机抽取了两张卡片，请用画树状图或列表的方法，求小涵抽到的两张卡片中恰好有数学家华罗庚卡通图案的概率.
21.(6分)如图,在 △ABC中， ∠C=90°,∠ABC的平分线BD交AC于点D，过点D作 DE⊥BD交AB于点E.
(1) 求证: △ADE∽△ABD；
(2) 若 AD=6,AE=4,， 则线段. BE= .
22. (8分)某超市以每件25元的进价购进一批商品. 当商品售价为40元时，八月份销售256件. 九、十月该商品十分畅销. 销售量持续走高. 在售价不变的基础上，十月底的销售量达到400件. 设九、十这两个月的月平均增长率不变.
(1) 求九、十这两个月的月平均增长率；
(2) 从十一月份起，超市决定采用降价促销的方式回馈顾客，经调查发现，在十一月份该商品每降价1元，销售量增加5件. 当商品降价多少元时，商场获利4250元?
23. (9分) 已知四边形ABCD 和四边形 CEGF 都是正方形.
(1) 如图1, 当点 G在对角线AC上时,AG= BE;
(2) 将正方形CEGF 绕着点 C顺时针旋转α; (0<α<360°)
①当正方形CEGF旋转到图2的位置时，(1)中的结论是否成立，请说明理由；
②在正方形 CEGF绕着点C顺时针旋转的过程中，当B，E，F三点共线时，直线CG与射线AD相交于点H，若 CF=22,BC=210,请直接写出线段AH的长.