
江苏连云港市海滨中学2024-2025学年八上数学第9周阶段性训练模拟练习【含答案】
展开A.44°B.58°C.64°D.68°
2.如图,数轴上点A对应的数是1,点B对应的数是2,BC⊥AB,垂足为B,且BC=1,以A为圆心,AC为半径画弧,交数轴于点D,则点D表示的数为( )
A.1.4B.C.D.2.4
3.如图,在长方形ABCD中,AB=8,BC=6,将其沿直线MN折叠,使点C与点A重合,CN的长为( )
A.7B.C.D.15
4.如图,在△ABC中,∠ACB=90°,AC=3,BC=4,AD平分∠CAB交BC于D点,E、F分别是AD,AC上的动点,则CE+EF的最小值为( )
A.1.8B.2C.2.4D.2.5
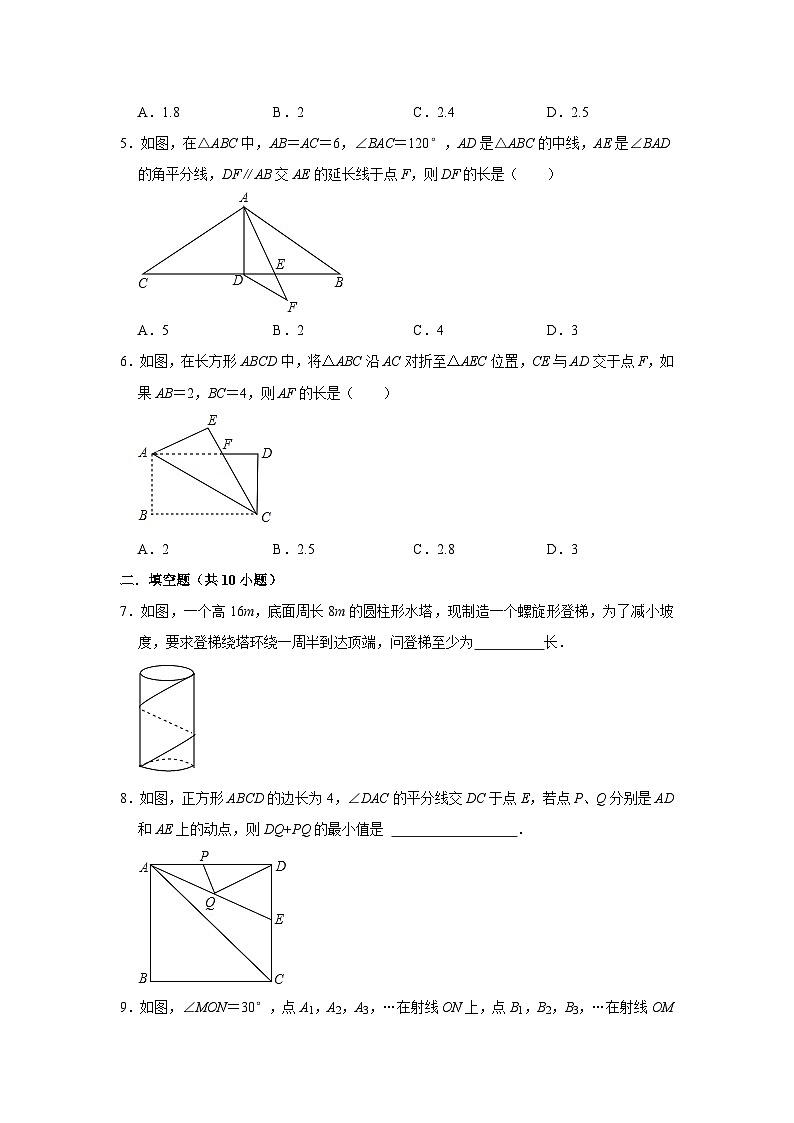
5.如图,在△ABC中,AB=AC=6,∠BAC=120°,AD是△ABC的中线,AE是∠BAD的角平分线,DF∥AB交AE的延长线于点F,则DF的长是( )
A.5B.2C.4D.3
6.如图,在长方形ABCD中,将△ABC沿AC对折至△AEC位置,CE与AD交于点F,如果AB=2,BC=4,则AF的长是( )
A.2B.2.5C.2.8D.3
二.填空题(共10小题)
7.如图,一个高16m,底面周长8m的圆柱形水塔,现制造一个螺旋形登梯,为了减小坡度,要求登梯绕塔环绕一周半到达顶端,问登梯至少为 长.
8.如图,正方形ABCD的边长为4,∠DAC的平分线交DC于点E,若点P、Q分别是AD和AE上的动点,则DQ+PQ的最小值是 .
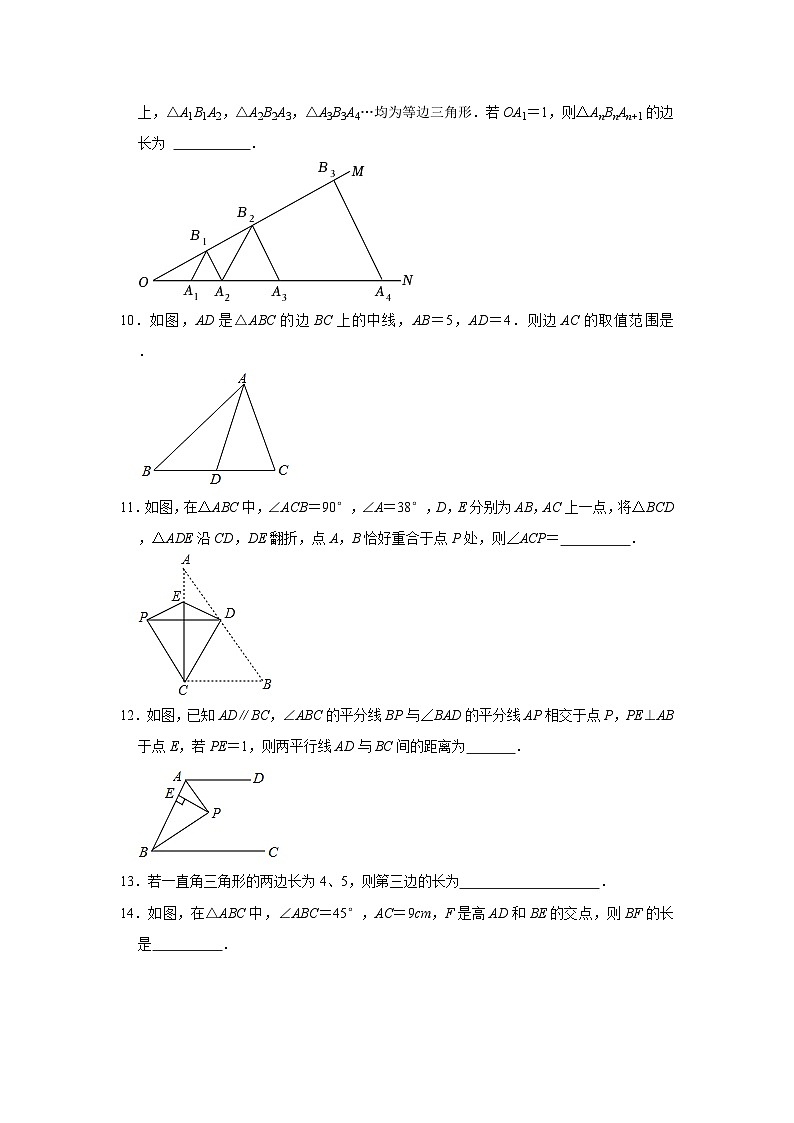
9.如图,∠MON=30°,点A1,A2,A3,…在射线ON上,点B1,B2,B3,…在射线OM上,△A1B1A2,△A2B2A3,△A3B3A4…均为等边三角形.若OA1=1,则△AnBnAn+1的边长为 .
10.如图,AD是△ABC的边BC上的中线,AB=5,AD=4.则边AC的取值范围是 .
11.如图,在△ABC中,∠ACB=90°,∠A=38°,D,E分别为AB,AC上一点,将△BCD,△ADE沿CD,DE翻折,点A,B恰好重合于点P处,则∠ACP= .
12.如图,已知AD∥BC,∠ABC的平分线BP与∠BAD的平分线AP相交于点P,PE⊥AB于点E,若PE=1,则两平行线AD与BC间的距离为 .
13.若一直角三角形的两边长为4、5,则第三边的长为 .
14.如图,在△ABC中,∠ABC=45°,AC=9cm,F是高AD和BE的交点,则BF的长是 .
15.如图,长方体的底面边长分别为1cm和2cm,高为4cm,点P在边BC上,且BP=BC.如果用一根细线从点A开始经过3个侧面缠绕一圈到达点P,那么所用细线最短需要 cm.
16.如图,在锐角△ABC中,AC=10,S△ABC=25,∠BAC的平分线交BC于点D,点M,N分别是AD和AB上的动点,则BM+MN的最小值是 .
三.解答题(共11小题)
17.如图,将直角三角形分割成一个正方形和两对全等的直角三角形,直角三角形ABC中,∠ACB=90°,BC=a,AC=b,AB=c,正方形IECF中,IE=EC=CF=FI=x.
(1)小明发明了求正方形边长的方法:
由题意可得BD=BE=a﹣x,AD=AF=b﹣x.
因为AB=BD+AD,所以a﹣x+b﹣x=c,解得x= .
(2)小亮也发现了另一种求正方形边长的方法:连接IC,利用S△ABC=S△AIB+S△AIC+S△BIC可以得到x与a、b、c的关系,请根据小亮的思路完成他的求解过程;
(3)请结合小明和小亮得到的结论验证勾股定理.(注:根据比例的基本性质,由可得ad=bc)
18.如图,△ABC中,∠ACB=90°,AB=5cm,BC=3cm,若点P从点A出发,以每秒2cm的速度沿折线A﹣C﹣B向点B运动,设运动时间为t秒(t>0)
(1)在AC上是否存在点P,使得PA=PB?若存在,求出t的值;若不存在,说明理由;
(2)若点P恰好在△ABC的角平分线上,请求出t的值,说明理由.
19.已知∠ACD=90°,MN是过点A的直线,AC=DC,DB⊥MN于点B,如图(1).易证BD+AB=CB,过程如下:
过点C作CE⊥CB于点C,与MN交于点E
∵∠ACB+∠BCD=90°,∠ACB+∠ACE=90°,∴∠BCD=∠ACE.
∵四边形ACDB内角和为360°,∴∠BDC+∠CAB=180°.
∵∠EAC+∠CAB=180°,∴∠EAC=∠BDC.
又∵AC=DC,∴△ACE≌△DCB,∴AE=DB,CE=CB,∴△ECB为等腰直角三角形,∴BE=CB.
又∵BE=AE+AB,∴BE=BD+AB,∴BD+AB=CB.
(1)当MN绕A旋转到如图(2)和图(3)两个位置时,BD、AB、CB满足什么样关系式,请写出你的猜想,并对图(3)给予证明.
(2)MN在绕点A旋转过程中,当∠BCD=30°,BD=时,则CD= ,CB= .
20.如图,等边△ABC中,AO是∠BAC的角平分线,D为AO上一点,以CD为一边且在CD下方作等边△CDE,连接BE.
(1)求证:AD=BE;
(2)已知AC=8,求点C到BE之间的距离.
21.如图所示,一架梯子AB斜靠在墙面上,且AB的长为2.5米.
(1)若梯子底端离墙角的距离OB为1.5米,求这个梯子的顶端A距地面有多高?
(2)在(1)的条件下,如果梯子的顶端A下滑0.5米到点A',那么梯子的底端B在水平方向滑动的距离BB'为多少米?
22.在长方形纸片ABCD中,AB=8,P是边BC上一点,BP=6.将纸片沿AP折叠后,点B的对应点记为点O,PO的延长线恰好经过该长方形的顶点D.
(1)试判断△ADP的形状,并说明理由;
(2)求AD长.
23.阅读材料并完成习题:
在数学中,我们会用“截长补短”的方法来构造全等三角形解决问题.请看这个例题:如图1,在四边形ABCD中,∠BAD=∠BCD=90°,AB=AD,若AC=5cm,求四边形ABCD的面积.
解:延长线段CB到E,使得BE=CD,连接AE,我们可以证明△BAE≌△DAC,根据全等三角形的性质得AE=AC=5,∠EAB=∠CAD,则∠EAC=∠EAB+∠BAC=∠DAC+∠BAC=∠BAD=90°,得S四边形ABCD=S△ABC+S△ADC=S△ABC+S△ABE=S△AEC,这样,四边形ABCD的面积就转化为等腰直角三角形EAC面积.
(1)根据上面的思路,我们可以求得四边形ABCD的面积为 cm2.
(2)请你用上面学到的方法完成下面的习题.
如图2,已知FG=FN=HM=GH+MN=5cm,∠G=∠N=90°,求五边形FGHMN的面积.
24.已知,△ABC是边长8cm的等边三角形,动点P以1cm/s的速度从点A出发,沿线段AB向点B运动,运动时间为t
(1)如图1,t= s时,△PBC是直角三角形;
(2)如图2,若另一动点Q从点B出发,沿线段BC向点C运动,如果动点P、Q分别以1cm/s和2cm/s的速度同时出发.设运动时间为t(s),那么t为何值时,△PBQ是直角三角形?
(3)如图3,若另一动点Q从点C出发,沿射线BC方向运动.连接PQ交AC于D.如果动点P、Q都以1cm/s的速度同时出发.请你猜想:在点P、Q的运动过程中,△PCD和△QCD的面积有什么关系?并说明理由.
25.已知:如图,∠BAC的角平分线与BC的垂直平分线DG交于点D,DE⊥AB,DF⊥AC,垂足分别为E、F.
(1)求证:BE=CF;
(2)若AF=6,△ABC的周长为20,求BC的长.
26.如图1,点P、Q分别是等边△ABC边AB、BC上的动点(端点除外),点P从顶点A、点Q从顶点B同时出发,且它们的运动速度相同,连接AQ、CP交于点M.
(1)求证:△ABQ≌△CAP;
(2)当点P、Q分别在AB、BC边上运动时,∠QMC变化吗?若变化,请说明理由;若不变,求出它的度数.
(3)如图2,若点P、Q在运动到终点后继续在射线AB、BC上运动,直线AQ、CP交点为M,则∠QMC变化吗?若变化,请说明理由;若不变,则求出它的度数.
27.问题:如图1,在Rt△ABC中,∠BAC=90°,AB=AC,D为BC边上一点(不与点B、C重合),将线段AD绕点A逆时针旋转90°得到AE,连接EC.
求证:△ABD≌△ACE;
探索:如图2,在Rt△ABC和Rt△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,将△ADE绕点A旋转,使点D落在BC边上,试探索线段AD2、BD2、CD2之间满足的数量关系,并证明你的结论;
应用:如图3,在四边形ABCD中,∠ABC=∠ACB=∠ADC=45°,若BD=6,CD=2,求AD的长.
参考答案与试题解析
一.选择题(共6小题)
1.【解答】解:如图连接OB、OC.
在△AOB和△AOC中,
,
∴△AOB≌△AOC,
∴OB=OC,
∵OD垂直平分AB,
∴OA=OB=OC,
∴∠OBA=∠OAB=∠OAC=∠OCA,设∠OBA=∠OAB=∠OAC=∠OCA=x.
∵∠OEC=136°,EO=EC,
∴∠EOC=∠ECO=(180°﹣∠OEC)=22°,
∴∠OBC=∠OCE=22°,
∵∠ABC+∠ACB+∠BAC=180°,
∴4x+2×22°=180°,
∴x=34°,
∴∠BAC=2x=68°,
故选:D.
2.【解答】解:在Rt△ABC中,AB=2﹣1=1,BC=1,
由勾股定理得,AC==,
则点D表示的数为+1.
故选:C.
3.【解答】解:∵将长方形ABCD沿直线MN折叠,使点C与点A重合,
∴AN=CN,
设CN=x,则AN=CN=x,
∵AB=8,
∴BN=8﹣x,
∵四边形ABCD为矩形,
∴∠B=90°,
在Rt△CBN中,CN2=NB2+BC2,
又∵BC=6,
∴x2=(8﹣x)2+62,
解得,x=,
故选:B.
4.【解答】解:∵∠ACB=90°,AC=3,BC=4,
∴AB==5,
在AB上取一点G,使AG=AF,
∵∠CAD=∠BAD,AE=AE,
∴△AEF≌△AEG(SAS),
∴FE=EG,
∴CE+EF=CE+EG,
则当点C,E,G三点在一条直线且CG垂直AB时,CG的值最小,
∵S△ABC=AC•BC=AB•CG,
∴3×4=5CG,
∴CG=,
∴CE+EF的最小值为,
故选:C.
5.【解答】解:∵△ABC是等腰三角形,D为底边的中点,
∴AD⊥BC,∠BAD=∠CAD,
∵∠BAC=120°,
∴∠BAD=60°,∠ADB=90°,
∵AE是∠BAD的角平分线,
∴∠DAE=∠EAB=30°,
∵DF∥AB,
∴∠F=∠BAE=30°,
∴∠DAF=∠F=30°,
∴AD=DF,
∵AB=6,∠B=30°,
∴AD=AB=3,
∴DF=3,
故选:D.
6.【解答】解:∵AD∥BC,
∴∠FAC=∠ACB,
由翻转变换的性质可知,∠FCA=∠ACB,
∴∠FAC=∠FCA,
∴FA=FC,
在Rt△CDF中,FC2=DF2+CD2,即FA2=(4﹣AF)2+22,
∴AF=2.5,
故选:B.
二.填空题(共10小题)
7.【解答】解:将圆柱表面切开展开呈长方形,
设等楼梯的长为xm,
∵圆柱高16m,底面周长8m,
∴x2=(1×8+4)2+162=400,
∴登梯至少=20(m),
故答案为:20m.
8.【解答】解:作DD′⊥AE于F,交AC于D′,再过D′作D′P′⊥AD于P′,
∵DD′⊥AE,
∴∠AFD=∠AFD′,
∵AF=AF,∠DAE=∠CAE,
∴△DAF≌△D′AF,
∴D′是D关于AE的对称点,AD′=AD=4,
∴D′P′即为DQ+PQ的最小值,
∵四边形ABCD是正方形,
∴∠DAD′=45°,
∴AP′=P′D′,
∴在Rt△AP′D′中,
P′D′2+AP′2=AD′2,AD′2=16,
∵AP′=P′D',
2P′D′2=AD′2,即2P′D′2=16,
∴P′D′=2,
即DQ+PQ的最小值为2,
故答案为:2.
9.【解答】解:∵△A1B1A2是等边三角形,
∴A1B1=A2B1,∠3=∠4=∠12=60°,
∴∠2=120°,
∵∠MON=30°,
∴∠1=180°﹣120°﹣30°=30°,
又∵∠3=60°,
∴∠5=180°﹣60°﹣30°=90°,
∵∠MON=∠1=30°,
∴OA1=A1B1=1,
∴A2B1=1,
∵△A2B2A3、△A3B3A4是等边三角形,
∴∠11=∠10=60°,∠13=60°,
∵∠4=∠12=60°,
∴A1B1∥A2B2∥A3B3,B1A2∥B2A3,
∴∠1=∠6=∠7=30°,∠5=∠8=90°,
∴A2B2=2B1A2,B3A3=2B2A3,
∴A3B3=4B1A2=4,
A4B4=8B1A2=8,
A5B5=16B1A2=16,
以此类推:△AnBnAn+1的边长为 2n﹣1.
故答案为:2n﹣1.
10.【解答】解:延长AD至E,使DE=AD,连接CE.
在△ABD与△ECD中,
,
∴△ABD≌△ECD(SAS),
∴CE=AB.
在△ACE中,AE﹣EC<AC<AE+EC,
∴8﹣5<AC<8+5,
即3<AC<13,
故答案为:3<AC<13.
11.【解答】解:在△ABC中,∠ACB=90°,∠A=38°,
∴∠B=180°﹣∠ACB﹣∠A=52°.
由折叠的性质可知:DA=DP=DB,∠DCP=∠DCB.
又∵△ABC为直角三角形,
∴DC=AB,
∴DC=DA=DB,
∴∠ACD=∠A=38°,∠DCB=∠B=52°,
∴∠DCP=52°,
∴∠ACP=∠DCP﹣∠ACD=52°﹣38°=14°.
故答案为:14°.
12.【解答】解:过点P作FG⊥AD交AD于F,交BC于G,
∵AD∥BC,
∴FG⊥BC,
∵AP是∠BAD的角平分线,PF⊥AD,PE⊥AB,
∴PF=PE=1,
∵BP是∠ABC的角平分线,PE⊥AB,PG⊥BC,
∴PG=PE=1,
∴两平行线AD与BC间的距离为PF+PG=2,
故答案为:2.
13.【解答】解:当4和5都是直角边时,则第三边是=;
当5是斜边时,则第三边是3.
故答案为:和3.
14.【解答】解:∵AD⊥BC,BE⊥AC,
∴∠ADC=∠ADB=90°,∠BEA=90°,
又∵∠FBD+∠BDF+∠BFD=180°,∠FAE+∠FEA+∠AFE=180°,且∠BFD=∠AFE,
∴∠FBD=∠FAE,
又∵∠ABC=45°,∠ABD+∠BAD=90°,
∴∠BAD=45°,
∴BD=AD,且∠ADC=∠BDF=90°,∠FBD=∠FAE,
∴△ADC≌△BDF(ASA)
∴BF=AC=9cm,
故答案为:9cm.
15.【解答】解:将长方体展开,连接A、P,
∵长方体的底面边长分别为1cm 和2cm,高为4cm,点P在边BC上,且BP=BC,
∴AC=4cm,PC=BC=3cm,
根据两点之间线段最短,AP==5(cm).
故答案为:5.
16.【解答】解:如图,∵AD是∠BAC的平分线,
∴点B关于AD的对称点B′在AC上,
过点B′作B′N⊥AB于N交AD于M,
由轴对称确定最短路线问题,点M即为使BM+MN最小的点,B′N=BM+MN,
过点B作BE⊥AC于E,
∵AC=10,S△ABC=25,
∴×10•BE=25,
解得BE=5,
∵AD是∠BAC的平分线,B′与B关于AD对称,
∴AB=AB′,
∴△ABB′是等腰三角形,
∴B′N=BE=5,
即BM+MN的最小值是5.
故答案为:5.
三.解答题(共11小题)
17.【解答】解:(1)∵a﹣x+b﹣x=c,
∴x=,
故答案为:;
(2)∵S△ABC=S△AIB+S△AIC+S△BIC,
∴,
解得x=,
即正方形IECF的边长是;
(3)由(1)和(2)可得,
=,
∴2ab=(a+b﹣c)(a+b+c),
∴2ab=[(a+b)﹣c][(a+b)+c],
∴2ab=(a+b)2﹣c2,
∴2ab=a2+2ab+b2﹣c2,
∴c2=a2+b2,
∴勾股定理成立.
18.【解答】解:(1)如图1,设存在点P,使得PA=PB,
此时PA=PB=2t,PC=4﹣2t,
在Rt△PCB中,
PC2+CB2=PB2,
即:(4﹣2t)2+32=(2t)2,
解得:t=,
∴当t=时,PA=PB;
(2)当点P在点C或点B处时,一定在△ABC的角平分线上,
此时t=2或t=3.5秒;
当点P在∠ABC的角平分线上时,作PM⊥AB于点M,如图2,
此时AP=2t,PC=PM=4﹣2t,
△APB的面积=PM•AB=BC•AP,
∴AP:AB=PM:BC,
即:2t:5=(4﹣2t):3,
解得:t=;
当点P在∠CAB的平分线上时,作PN⊥AB,如图3,
此时BP=7﹣2t,PN=PC=(2t﹣4),
△APB的面积=PN•AB=BP•AC,
∴BP:BA=PN:AC,
即:(7﹣2t):5=(2t﹣4):4,
解得:t=,
综上,当t=2s或3.5s或s或s时,点P在△ABC的角平分线上.
19.【解答】解:(1)如图(2):AB﹣BD=CB.理由如下:
过点C作CE⊥CB于点C,与MN交于点E,
∵∠ACD=90°,
∴∠ACE=90°﹣∠DCE,∠BCD=90°﹣∠ECD,
∴∠BCD=∠ACE.
∵DB⊥MN,
∴∠CAE=90°﹣∠AFC,∠D=90°﹣∠BFD,
∵∠AFC=∠BFD,
∴∠CAE=∠D,
在△ACE和△DCB中,,
∴△ACE≌△DCB(ASA),
∴AE=DB,CE=CB,
∴△ECB为等腰直角三角形,
∴BE=CB.
又∵BE=AB﹣AE,
∴BE=AB﹣BD,
∴AB﹣BD=CB.
如图(3):BD﹣AB=CB.理由如下:
:过点C作CE⊥CB于点C,与MN交于点E,
∵∠ACD=90°,
∴∠ACE=90°+∠ACB,∠BCD=90°+∠ACB,
∴∠BCD=∠ACE.
∵DB⊥MN,
∴∠CAE=90°﹣∠AFB,∠D=90°﹣∠CFD,
∵∠AFB=∠CFD,
∴∠CAE=∠D,
又∵AC=DC,
∴△ACE≌△DCB,
∴AE=DB,CE=CB,
∴△ECB为等腰直角三角形,
∴BE=CB.
又∵BE=AE﹣AB,
∴BE=BD﹣AB,
∴BD﹣AB=CB.
(2)MN在绕点A旋转过程中,这个的意思并没有指明是哪种情况,
∴综合了第一个图和第二个图两种情况,
若是第1个图:由(1)得:△ACE≌△DCB,CE=CB,
∴△ECB为等腰直角三角形,
∴∠AEC=45°=∠CBD,
过D作DH⊥CB.则△DHB为等腰直角三角形.
BD=BH,
∴BH=DH=1.
直角△CDH中,∠DCH=30°,
∴CD=2DH=2,CH=.
∴CB=+1;
若是第二个图:过D作DH⊥CB交CB延长线于H.
解法类似上面,CD=2,得出CB=﹣1;
故答案为:2,+1或﹣1.
20.【解答】(1)证明:
∵△ABC和△CDE为等边三角形,
∴CD=CE,AC=BC,∠ACB=∠DCE=60°,
∴∠ACD=∠BCE,
在△ACD和△BCE中
∴△ACD≌△BCE(SAS),
∴AD=BE;
(2)解:
由(1)可知△ACD≌△BCE,
∴S△ACD=S△BCE,
设C到BE的距离为h,则AD•CO=BE•h,
∴h=CO,
∵AO平分∠BAC,
∴CO=BC=AC=4,
即点C到BE的距离为4.
21.【解答】解:(1)根据勾股定理:
所以梯子距离地面的高度为:AO=(米);
(2)梯子下滑了0.5米即梯子距离地面的高度为OA′=(2﹣0.5)=1.5(米),
根据勾股定理:OB′==2(米),
所以当梯子的顶端下滑0.5米时,梯子的底端水平后移了2﹣1.5=0.5(米),
答:当梯子的顶端下滑0.5米时,梯子的底端水平后移了0.5米.
22.【解答】解:(1)△ADP为等腰三角形;
理由:由翻折可得∠APB=∠APD,
∵四边形ABCD是长方形,
∴AD∥BC,
∴∠DAP=∠APB,
∴∠DAP=∠APD,
∴AD=DP,
∴△ADP为等腰三角形;
(2)由翻折可知PO=BP=6,AO=AB=8,∠AOD=∠AOP=∠B=90°,
设AD的长为x.
∵AD=DP,
∴OD=x﹣6,
在直角△AOD中有AD2=AO2+OD2,
∴x2=64+(x﹣6)2,
解得x=,
即AD的长为.
23.【解答】解:(1)由题意可得,
AE=AC=5,∠EAC=90°,
则△EAC的面积是:(cm2),
即四边形ABCD的面积为12.5cm2,
故答案为:12.5;
(2)连接FH、FM,延长MN到O,截取NO=GH,
在△GFH和△NFO中,
,
∴△GFH≌△NFO(SAS),
∴FH=FO,
∵FG=FN=HM=GH+MN=2cm,GH=NO,
∴HM=OM,
在△HFM和△OFM中,
,
∴△HFM≌△OFM(SSS),
∵△OFM的面积是:cm2,
∴△HFM的面积是12.5cm2,
∴四边形HFOM的面积是25cm2,
∴五边形FGHMN的面积是25cm2.
24.【解答】解:当△PBC是直角三角形时,∠B=60°,
而∠BPC=90°,则∠BCP=30°,
∴BP=BC=4,
所以t=4(s),
故答案为4;
(2)当∠BPQ=90°时,BP=0.5BQ,
而BP=8﹣2t,BQ=2t,
∴8﹣t=0.5×2t,所以t=4;
当∠BQP=90°时,BP=2BQ,
∴8﹣t=2×2t,所以t=;
所以t=4或;
(3)相等,如图所示:
作PE垂直AD,QG垂直AD延长线,则PE∥QG,
∴∠G=∠AEP,
在△EAP和△GCQ,
,
∴△EAP≌△GCQ(AAS),
∴PE=QG,
∴△PCD和△QCD同底等高,
所以面积相等.
25.【解答】(1)证明:连接DB、DC.
∵AD平分∠BAC,DE⊥AB,DF⊥AC,
∴DE=DF,
∵DG垂直平分BC,
∴DB=DC,
在Rt△BED和Rt△CFD中,
,
∴Rt△BED≌Rt△CFD(HL),
∴BE=CF;
(2)解:∵∠DAE=∠DAF,∠AED=∠AFD=90°,AD=AD,
∴△AED≌△AFD(AAS),
∴AF=AE=6,
由(1)得:BE=CF,
∵△ABC的周长=AB+AC+BC,
=AE+EB+AF﹣CF+BC,
=AE+AF+BC=20,
∴BC=20﹣12=8.
26.【解答】(1)证明:∵△ABC是等边三角形
∴∠ABQ=∠CAP,AB=CA,
又∵点P、Q运动速度相同,
∴AP=BQ,
在△ABQ与△CAP中,
∵,
∴△ABQ≌△CAP(SAS);
(2)解:点P、Q在运动的过程中,∠QMC不变.
理由:∵△ABQ≌△CAP,
∴∠BAQ=∠ACP,
∵∠QMC=∠ACP+∠MAC,
∴∠QMC=∠BAQ+∠MAC=∠BAC=60°…(6分)
(3)解:点P、Q在运动到终点后继续在射线AB、BC上运动时,∠QMC不变.(7分)
理由:∵△ABQ≌△CAP,
∴∠BAQ=∠ACP,
∵∠QMC=∠BAQ+∠APM,
∴∠QMC=∠ACP+∠APM=180°﹣∠PAC=180°﹣60°=120°.
27.【解答】问题:
证明:在Rt△ABC中,AB=AC,
∴∠B=∠ACB=45°,
∵∠BAC=∠DAE=90°,
∴∠BAC﹣∠DAC=∠DAE﹣∠DAC,即∠BAD=∠CAE,
在△BAD和△CAE中,
,
∴△BAD≌△CAE(SAS),
探索:
解:结论:2AD2=BD2+CD2,
理由是:如图2中,连接EC.
∵∠BAC=∠DAE=90°,
∴∠BAD=∠CAE,
在△ABD和△ACE中,
,
∵△BAD≌△CAE(SAS),
∴BD=CE,∠B=∠ACE=45°,
∴∠BCE=∠ACB+∠ACE=45°+45°=90°,
∴DE2=CE2+CD2,
Rt△ADE中,DE2=AD2+AE2=2AD2,
∴2AD2=BD2+CD2;
应用:
解:如图3,将AD绕点A逆时针旋转90°至AG,连接CG、DG,
则△DAG是等腰直角三角形,
∴∠ADG=45°,
∵∠ADC=45°,
∴∠GDC=90°,
同理得:△BAD≌△CAG,
∴CG=BD=6,
Rt△CGD中,∵CD=2,
∴DG====4,
∵△DAG是等腰直角三角形,
∴AD=AG=4.书面同意
江苏无锡市东林中学2024-2025学年七上数学第10周阶段性训练模拟练习【含答案】: 这是一份江苏无锡市东林中学2024-2025学年七上数学第10周阶段性训练模拟练习【含答案】,共13页。试卷主要包含了已知a、b的大致位置如图所示等内容,欢迎下载使用。
江苏无锡市东林中学2024-2025学年八上数学第10周阶段性训练模拟练习【含答案】: 这是一份江苏无锡市东林中学2024-2025学年八上数学第10周阶段性训练模拟练习【含答案】,共20页。试卷主要包含了给出下列4个命题等内容,欢迎下载使用。
江苏连云港市海滨中学2024-2025学年七上数学网络提高班第9周阶段性训练模拟练习【含答案】: 这是一份江苏连云港市海滨中学2024-2025学年七上数学网络提高班第9周阶段性训练模拟练习【含答案】,共9页。试卷主要包含了定义运算a*b=,已知多项式3x2﹣2,大于﹣π并且不是自然数的整数有等内容,欢迎下载使用。












