2023-2024学年广东省深圳市龙岗区六年级上册期末数学试卷

这是一份2023-2024学年广东省深圳市龙岗区六年级上册期末数学试卷，共16页。试卷主要包含了下列说法中正确的是，圆的半径和它的周长比是等内容，欢迎下载使用。
A．圆周率就是3.14。
B．由于圆的位置不同，所以圆的周长不同。
C．直径是圆内最长的线段。
D．直径是线段，半径是射线。
2．圆的半径和它的周长比是（ ）
A．1：πB．2：πC．1：2πD．2π：1
3．甲数比乙数多20%，甲数与乙数的最简整数比是（ ）。
A．5：4B．6：5C．4：5D．5：6
4．一个半圆的半径是3厘米，它的周长是（ ）厘米。
A．18.84B．9.42C．12.42D．15.42
5．有9人要参加羽毛球比赛，如果每两个人之间要比一场，一共要比（ ）场
A．72B．36C．54D．27
6．要了解上半年深圳每月房价的变化情况，最好选用（ ）统计图。
A．扇形B．条形C．折线D．复式条形
7．一个立体图形，从正面看到的形状是，从左面看到的形状是，搭这样的立体图形，至少要（ ）个小立方体。
A．5B．6C．7D．8
8．一件上衣原价1000元，先提价20%，再降价20%，现价（ ）
A．比原价低B．比原价高C．和原价相等D．无法确定
9．一件衣服原价是300元，优惠价是240元，优惠价比原价便宜了（ ）
A．20%B．25%C．60%D．80%
10．鸡兔同笼，共有25个头，80条腿，那么兔和鸡的只数比是（ ）
A．3：2B．2：3C．1：3D．3：1
11．将圆剪拼成一个长方形，这个长方形的长等于（ ）
A．rB．πrC．2πrD．πr2
12．化成最简整数比是（ ）
A．1：7B．8：7C．7：8D．7：16
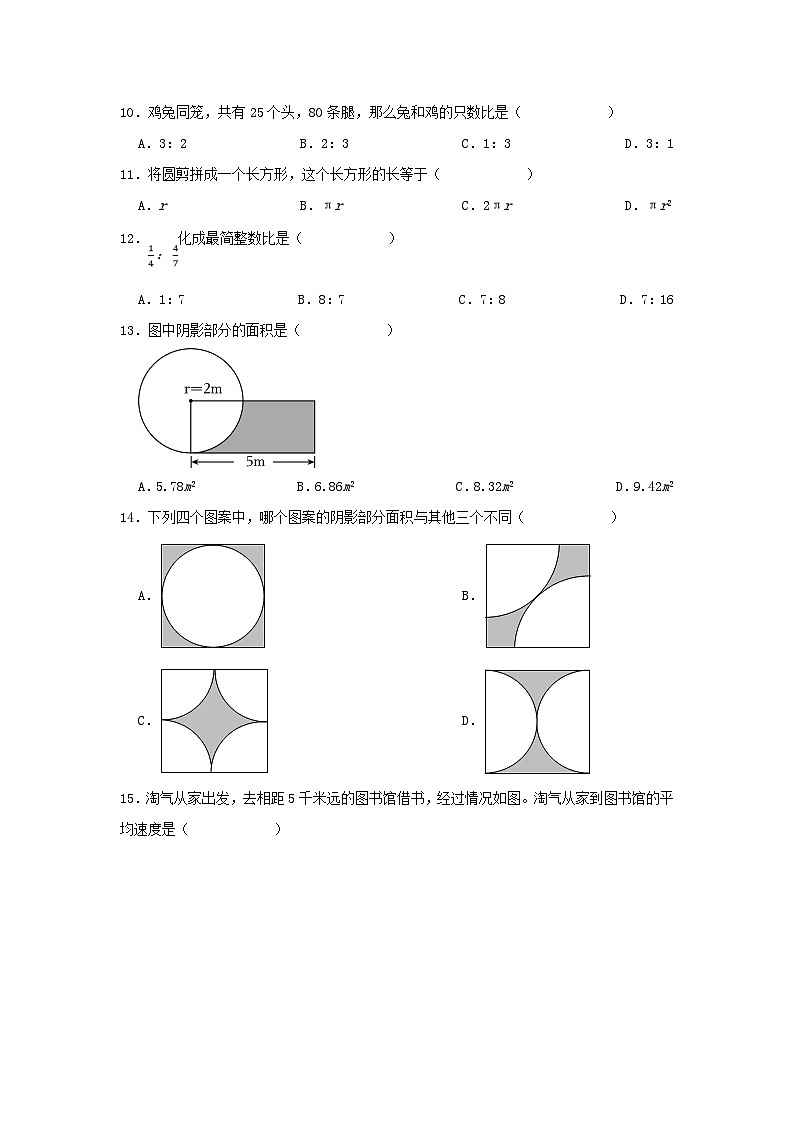
13．图中阴影部分的面积是（ ）
A．5.78m2B．6.86m2C．8.32m2D．9.42m2
14．下列四个图案中，哪个图案的阴影部分面积与其他三个不同（ ）
A．B．
C．D．
15．淘气从家出发，去相距5千米远的图书馆借书，经过情况如图。淘气从家到图书馆的平均速度是（ ）
A．5千米/时B．1.25千米/时
C．千米/时D．56千米/时
16．9÷ ＝ ＝12： ＝ %＝六成。
17． 米比50米多20%。
18．如果甲比乙多25%，则乙比甲少 %。
19．一个三角形的三个内角度数的比是3：4：8，那么它是一个 三角形。
20．一件衣服打九折销售，现价比原价便宜 %。
21．两个圆的半径之比是3：5，它们的面积之比是 ．
22．在5：7中，比的前项加上15，要使比值不变，后项应加上 。
23．配制200克盐水，含盐率为10%，需要盐 克。
24．把周长为18.84厘米的圆平均分成两个半圆，每个半圆的面积是 平方厘米。
25．淘气和奇思完成同一张练习，淘气用了25分钟，奇思用了半小时，淘气和奇思完成此练习的速度比是 。
26．化简比。
27．递等式计算，能简算的要简算。
28．解方程。
29．在如图的正方形中画一个最大的圆。
30．表是淘气家和笑笑家2023年1～6月份用水量统计表。（单位：吨）
请根据表完成淘气家和笑笑家2023年1～6月份用水量变化情况的折线统计图。
31．张叔叔买了五年期的国家建设债券15000元，年利率是3.8%。到期时，张叔叔可拿到的本金和利息一共有多少元？
32．一辆小汽车从甲地开往乙地，已走的路程与剩下路程的比是3：7，这时离中点还有120千米。甲地到乙地的路程有多少千米？
33．实验小学十月份用水120立方米，比九月份节约了30立方米，十月份比九月份节约用水百分之几？
34．如图，已知小圆半径是5米，大圆半径是7米，阴影部分的面积是多少平方米？
35．淘气调查了六（1）班学生“我最喜欢的科目”情况，绘制成统计图。喜欢数学的人数比喜欢英语的人数多6人。喜欢语文的有多少人？
答案解析部分
1．【答案】C
【知识点】圆、圆心、半径与直径的认识；圆的周长
【解析】【解答】解：A：圆周率的近似数是3.14，原来说法错误；
B：圆的周长与圆的位置无关，原来说法错误；
C：直径是圆内最长的线段，此说法正确；
D：直径和半径都是线段，原来说法错误。
故答案为：C。
【分析】A：圆周率是一个无限不循环小数，3.14是其近似数；
B：圆的周长与圆的直径或半径的大小有关，与圆的位置无关；
C：直径是通过圆心并且两端都在圆上的线段，直径是圆内最长的线段；
D：半径是连接圆心到圆上任意一点的线段，直径和半径都是线段。
2．【答案】C
【知识点】圆的周长；比的化简与求值
【解析】【解答】解：圆的半径和它的周长比是1：2π。
故答案为：C。
【分析】圆的周长是直径的π倍，是半径的2π倍，所以圆的半径和它的周长的比是1：2π。
3．【答案】B
【知识点】比的化简与求值
【解析】【解答】设乙数为1，则甲数为1+20%，
甲数∶乙数=（1+20%）∶1
=1.2∶1
=6∶5。
故答案为：B。
【分析】设乙数为1，则可得出甲数为1+20%，再将甲数与乙数相比即可，最后根据比的基本性质化成最简整数比即可。
比的基本性质：比的前项和后项同时乘或除以同一个不为0的数，比值不变。
4．【答案】D
【知识点】圆的周长
【解析】【解答】解：3.14×3+3×2
=9.42+6
=15.42（厘米）
故答案为：D。
【分析】圆周长公式：C=2πr。半圆的周长包括圆周长的一半和一条直径的长度。由此用圆周长的一半加上直径的长度即可求出半圆的周长。
5．【答案】B
【知识点】排列组合
【解析】【解答】解：8+7+6+5+4+3+2+1=36（场）
故答案为：B。
【分析】第一人要与后面8人比赛8场；第二人要与后面7人比赛7场，……，第8人要与最后一人比赛1场，这样求出总场次即可。也可以根据“场数=人数×（人数-1）÷2”来计算。
6．【答案】C
【知识点】统计图的选择
【解析】【解答】解：要了解上半年深圳每月房价的变化情况，因为要表示出价格的增减变化，最好选用折线统计图。
故答案为：C。
【分析】条形统计图能表示数量的多少；折线统计图不仅能表示数量的多少，还能表示数量的增减变化情况；扇形统计图能表示部分与整体之间的关系。
7．【答案】B
【知识点】根据观察到的图形确定几何体
【解析】【解答】解：一个立体图形，从正面看到的形状是，从左面看到的形状是，搭这样的立体图形，至少要6个小立方体。
故答案为：B。
【分析】根据从左面看到的图形可知，图形有2层，根据从正面看到的图形可以判断下层至少需要4个正方体，上层至少需要2个正方体，所以至少需要6个小立方体。
8．【答案】A
【知识点】百分数的其他应用
【解析】【解答】解：1000×（1+20%）×（1-20%）
=1000×120%×80%
=1200×80%
=960（元）
1000＞960，所以现价比原价低。
故答案为：A。
【分析】以原价为单位“1”，提价后的价格是原价的（1+20%），降价后的价格又是提价后价格的（1-20%），根据分数乘法的意义求出现价，然后与原价比较即可。
9．【答案】A
【知识点】百分数的应用--增加或减少百分之几
【解析】【解答】解：（300-240）÷300
=60÷300
=20%
故答案为：A。
【分析】以原价为单位“1”，用优惠价比原价少的钱数除以原价即可求出优惠价比原价便宜了百分之几。
10．【答案】A
【知识点】比的化简与求值；鸡兔同笼问题
【解析】【解答】解：兔的只数：
（80-25×2）÷（4-2）
=30÷2
=15（只）
鸡：25-15=10（只）
兔和鸡的只数比是：15：10=3：2。
故答案为：A。
【分析】假设都是鸡，则共50条腿，比80条腿少，是因为把兔也当作2条腿来计算了，这样每只兔就少算了2条腿。因此把一共少的腿数除以每只兔子少的腿数即可求出兔子的只数，进而求出鸡的只数。然后写出兔和鸡的只数比即可。
11．【答案】B
【知识点】圆的面积
【解析】【解答】解：将圆剪拼成一个长方形，这个长方形的长等于圆周长的一半，也就是πr。
故答案为：B。
【分析】将圆剪拼成一个长方形，长方形的长就是圆周长的一半，宽就是圆的半径。
12．【答案】D
【知识点】比的化简与求值
【解析】【解答】解：=（×28）：（×28）=7：16
故答案为：D。
【分析】根据比的基本性质，把比的前项和后项同时乘前项和后项分母的最小公倍数，这样就能化成最简整数比。
13．【答案】B
【知识点】圆的面积
【解析】【解答】解：5×2-3.14×22÷4
=10-3.14
=6.86（m2）
故答案为：B。
【分析】阴影部分的面积是长方形面积减去长方形内空白部分的面积，空白部分是半径2米的圆的面积除以4。
14．【答案】B
【知识点】圆的面积
【解析】【解答】、、三个图形用阴影部分的面积都是正方形面积减去正方形内最大圆的面积；中阴影部分的面积与其他三个不同。
故答案为：B。
【分析】A：阴影部分的面积是正方形面积减去最大圆的面积；
B：空白部分是两个圆，这两个空白部分与正方形内最大圆的面积不相等；
C：空白部分四个圆刚好是正方形内最大的圆；
D：空白部分两个半圆合起来刚好是正方形内最大的圆。
15．【答案】C
【知识点】从单式折线统计图获取信息
【解析】【解答】解：5÷1.5=（千米/时）
故答案为：C。
【分析】从家到图书馆共5千米，用时1.5小时，用路程除以时间求出平均速度即可。
16．【答案】15；18；20；60
【知识点】百分数的应用--成数
【解析】【解答】解：六成=60%，9÷60%=15；30×60%=18；12÷60%=20；所以9÷15==12：20=60%=六成。
故答案为：15；18；20；60。
【分析】六成就是60%，是除法的商，分数的分数值，比的比值。可以根据分数、比、除法之间的关系确定除数、分子或后项。也可以用被除数除以商求出除数，用分母乘分数值求出分子，用前项除以比值求出后项。
17．【答案】60
【知识点】百分数的应用--增加或减少百分之几
【解析】【解答】解：50×（1+20%）
=50×120%
=60（米）
故答案为：60。
【分析】以50米为单位“1”，比50米多20%的长度是50米的（1+20%），根据分数乘法的意义计算即可。
18．【答案】20
【知识点】百分数的应用--增加或减少百分之几
【解析】【解答】解：25%÷（1+25%）
=25%÷125%
=20%
故答案为：20。
【分析】乙是“1”，则甲就是（1+25%）。用乙比甲少的除以甲即可求出乙比甲少百分之几。
19．【答案】钝角
【知识点】三角形的分类；比的应用
【解析】【解答】解：180°×=96°，是一个钝角三角形。
故答案为：钝角。
【分析】根据三个内角度数的比可知，最大角度数是三角形内角和的，根据分数乘法的意义求出最大角的度数，然后判断三角形的类型。
20．【答案】10
【知识点】百分数的应用--折扣
【解析】【解答】解：1-90%=10%
故答案为：10。
【分析】九折销售的意思就是现价是原价的90%，原价是“1”，用1减去90%即可求出现价比原价便宜百分之几。
21．【答案】9：25
【知识点】圆的面积
【解析】【解答】解：两个圆的半径之比是3：5，它们的面积之比是32：52=9：25。
故答案为：9：25。
【分析】圆面积公式：S=πrr2，所以两个圆的面积比是两个圆半径平方的比。
22．【答案】21
【知识点】比的基本性质
【解析】【解答】解：5+15=20，20÷5=4，后项应加上7×4-7=21。
故答案为：21。
【分析】用原来的前项加上15求出现在的前项，计算出前项扩大的倍数，根据比的基本性质把后项也扩大相同的倍数，然后求出后项应加上的数即可。
23．【答案】20
【知识点】百分率及其应用
【解析】【解答】解：200×10%=20（克）
故答案为：20。
【分析】含盐率是盐的质量占盐水质量的百分率，用盐水的质量乘含盐率即可求出盐的质量。
24．【答案】14.13
【知识点】圆的面积
【解析】【解答】解：18.84÷3.14÷2=3（厘米），面积：3.14×32÷2=28.26÷2=14.13（平方厘米）。
故答案为：14.13。
【分析】圆周长公式：C=2πr=πd，圆面积公式：SS=πr2。用周长除以3.14再除以2求出半径，然后计算半圆的面积即可。
25．【答案】6：5
【知识点】比的化简与求值
【解析】【解答】解：：=6：5
故答案为：6：5。
【分析】半小时是30分钟。把任务总量看作“1”，用分数分别表示出两人的速度，写出速度的比并化成最简整数比即可。
26．【答案】解：3.6：6=36：60=（36÷12）：（60÷12）=3：5
：2.4=（×5）：（2.4×5）=6：12=1：2
时：20分=45分：20分=9：4
【知识点】比的化简与求值
【解析】【分析】比的基本性质：比的前项和后项同时乘或除以一个数（0除外），比值不变。
第一题：把比的前项和后项同时扩大10倍先化成整数比，然后除以前项和后项的最大公因数即可化成最简整数比；
第二题：把比的前项和后项同时乘5化成整数比，再化成最简整数比；
第三题：把时换算成分，然后根据比的基本性质化简比即可。
27．【答案】解：×12.5%+×0.125
=（+）×0.125
=1×0.125
=0.125
=+-
=-
=
【知识点】分数四则混合运算及应用；含百分数的计算
【解析】【分析】第一题：把百分数化成小数，同时运用乘法分配律简便计算；
第二题：先算除法，然后通分后按照从左到右的顺序计算。
28．【答案】
解：29%x-+=+
29%x÷29%=÷29%
x＝
解： x÷=÷
x＝
【知识点】列方程解关于百分数问题
【解析】【分析】等式的性质1：等式两边同时加上或减去同一个数，左右两边仍然相等；等式的性质2：等式两边同时乘一个数，或同时除以一个不是0的数，两边仍然相等。第一题：先把方程两边同时加上，然后同时除以29%即可求出未知数的值。第二题：先计算方程左边能计算的部分，然后同时除以即可求出未知数的值。
29．【答案】解：如图：
​​​​​​​
【知识点】画圆
【解析】【分析】画出正方形的两条对角线，两条对角线的交点就是最大圆的圆心。最大圆的半径是正方形边长的一半。由此用圆规画出正方形内最大的圆即可。
30．【答案】解：如图：
【知识点】复式折线统计图的特点及绘制
【解析】【分析】横轴表示月份，竖轴表示用水量；淘气家用实线表示，笑笑家用水量用虚线表示。根据统计表中的数据在统计图中先描点，然后依次连线绘制出折线统计图即可。
31．【答案】解：15000×3.8%×5+15000
=2850+15000
=17850（元）
答：张叔叔可拿到的本金和利息一共有17850元。
【知识点】百分数的应用--利率
【解析】【分析】利息=本金×利率×存期，根据公式先计算出利息，然后把本金和利息相加求出张叔叔可拿到的本金和利息总数即可。
32．【答案】解：120×2÷（7-3）
=240÷4
=60（千米）
60×（3+7）=600（千米）
答：甲地到乙地的路程有600千米。
【知识点】比的应用
【解析】【分析】此时离中点还有120千米，那么剩下的路程比已走的路程多了2个120千米，因此用多的千米数除以多的份数求出每份的长度。用每份的长度乘总份数即可求出两地的路程。
33．【答案】解：30÷（120+30）
=30÷150
=20%
答：十月份比九月份节约用水20%。
【知识点】百分数的应用--增加或减少百分之几
【解析】【分析】以九月份的用水量为单位“1”，用十月份的用水量加上30求出九月份的用水量，然后用节约的用水量除以九月份的用水量即可求出十月比九月节约用水百分之几。
34．【答案】解：3.14×（72-52）
=3.14×（49-25）
=3.14×24
=75.36（平方米）
答：阴影部分的面积是75.36平方米。
【知识点】圆环的面积
【解析】【分析】圆环的面积公式：S=π（R2-r2），根据公式计算圆环的面积即可。
35．【答案】解：6÷（32%-20%）
=6÷12%
=50（人）
50×24%=12（人）
答：喜欢语文的有12人。
【知识点】从扇形统计图获取信息
【解析】【分析】以调查的总人数为单位“1”，根据分数除法的意义用喜欢数学的人数比喜欢英语的人数多6人除以多的6人占总人数的百分率即可求出调查总人数。然后根据分数乘法的意义用调查总人数乘24%即可求出喜欢语文的人数。阅卷人
一、我会选。
得分
阅卷人
二、我会填。
得分
阅卷人
三、我会算。
得分
3.6：6
：2.4
时：20分
阅卷人
四、我会画。
得分
月份
1
2
3
4
5
6
淘气家
5
12
20
25
27
28
笑笑家
8
15
22
25
26
30
阅卷人
五、我会解决问题。
得分