甘肃省武威市凉州区武威九中片联考2023-2024学年九年级上学期1月期末数学试题(含解析)

这是一份甘肃省武威市凉州区武威九中片联考2023-2024学年九年级上学期1月期末数学试题(含解析)，共30页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
九年级数学
一、选择题（每小题3分，30分）
1．下列图形中，既是轴对称图形，又是中心对称图形的是（ ）
A． B． C． D．
2．从，，3三个数中随机取一个数作为a，则使抛物线的开口向下的概率是（ ）
A．B．C．D．
3．抛物线与x轴有两个不同的交点，则a的取值范围是（ ）
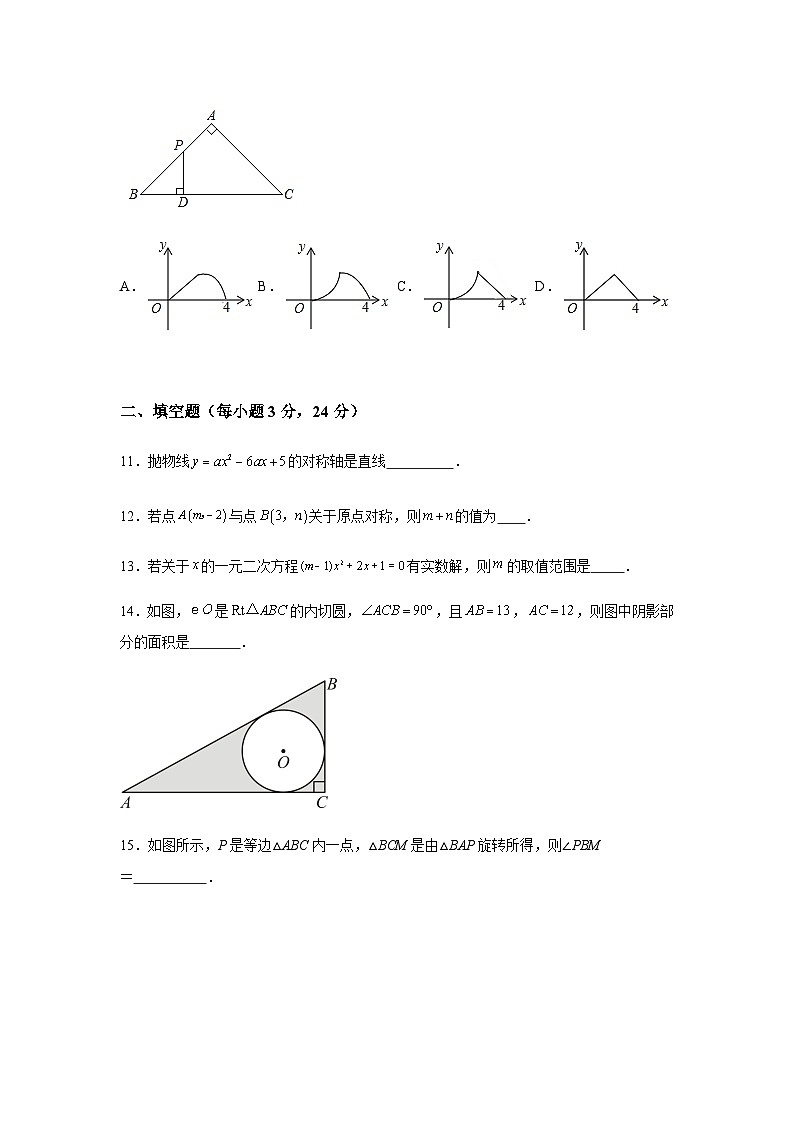
A．且B．
C．且D．
4．下列各组条件中，不能判定三角形与三角形相似的是（ ）
A．，B．，
C．，D．
5．抛物线先向左平移1个单位，再向下平移3个单位，所得抛物线是（ ）
A．B．
C．D．
6．若，，为二次函数图象上的三点，则，，的大小关系是（ ）
A．B．C．D．
7．若一个圆锥的侧面积是底面积的2倍，则圆锥侧面展开图的扇形的圆心角为 （ ）
A．120°B．180°C．240°D．300°
8．如图，从圆外一点引圆的两条切线，，切点分别为，，如果， ，那么弦AB的长是（ ）
A．B．C．D．
9．在Rt△ABC中，∠C=90°，AB=10．若以点C为圆心，CB为半径的圆恰好经过AB的中点D，则AC=（）
A．5B．C．D．6
10．如图，△ABC是等腰直角三角形，∠A=90°，BC=4，点P是△ABC边上一动点，沿B→A→C的路径移动，过点P作PD⊥BC于点D，设BD=x，△BDP的面积为y，则下列能大致反映y与x函数关系的图象是（ ）
A．B．C．D．
二、填空题（每小题3分，24分）
11．抛物线的对称轴是直线 ．
12．若点与点关于原点对称，则的值为 ．
13．若关于的一元二次方程有实数解，则的取值范围是 ．
14．如图，是的内切圆，，且，，则图中阴影部分的面积是 ．

15．如图所示，P是等边△ABC内一点，△BCM是由△BAP旋转所得，则∠PBM＝ ．
16．若，则 ．
17．在一个不透明的袋子里装有5个红球和若干个白球，它们除颜色外其余完全相同，通过多次摸球试验后发现，摸到红球的频率稳定在附近，则估计袋中的白球大约有 个．
18．二次函数的图象如图，给出下列四个结论：①；②；③；④；⑤．其中结论正确的个数是 ．
三、解答题（66分）
19．计算与解方程：
(1)；
(2)．
20．已知关于x的方程．
(1)若此方程的一个根为1，求m的值；
(2)求证：不论m取何实数，此方程都有两个不相等的实数根．
21．如图，在平面直角坐标系中，点O为坐标原点，已知三个顶点坐标分别为，，．
(1)画出关于x轴对称的，点A，B，C的对称点分别是点，，，直接写出点的坐标：____________；
(2)画出绕原点O顺时针旋转后得到的，并求出所扫过的面积是_____．
22．中国共产党第二十次全国代表大会胜利召开，是具有里程碑意义的大会，必将对中国和世界产生深远影响，某校积极组织学生学习二十大相关会议精神，并组织了二十大知识问答赛，将比赛结果分为A，B，C，D四个等级，根据如下不完整的统计图解答下列问题：
(1)求该校参加知识问答赛的学生人数；
(2)现准备从结果为A级的4人（两男两女）中随机抽取两名同学参加二十大宜讲，请用列表或画树状图的方法，求恰好抽到一名男生和一名女生参加宣讲活动的概率．
23．2023年清明节来临之际，某电影院开展“清明祭英烈，共铸中华魂”系列活动，对团体购买《长津湖》电影票实行优惠，决定在原定零售票价基础上每张降价16元，这样按原定零售票价需花费2000元购买的门票，现在只花费了1200元．
(1)求每张电影票的原定零售票价；
(2)为了弘扬爱国主义精神，该影院决定对网上购票的个人也采取优惠，原定零售票价经过连续两次降价后票价为每张32.4元，求平均每次降价的百分率．
24．如图，在△ABC中， 点D，E，F分别在AB，BC，AC边上，，．
(1)求证：；
(2)若，△EFC的面积为20， 求△ABC的面积．
25．如图，为的直径，过圆上一点作的切线交的延长线与点，过点作交于点，连接．
(1)求证：与相切；
(2)若，，求的长．
26．某校数学活动小组探究了如下数学问题：
(1)问题发现：如图1，中，，．点是底边上一点，连接，以为腰作等腰，且，连接、则和的数量关系是___________；
(2)变式探究：如图2，中，，．点是腰上一点，连接，以为底边作等腰，连接，判断和的数量关系，并说明理由；
(3)问题解决；如图3，正方形的边长为10，点是边上一点，以为对角线作正方形，连接．若设正方形的面积为，．求与的函数关系式．
27．如图，已知抛物线的对称轴为直线，且经过，两点，与轴的另一个交点为．
(1)求抛物线的函数表达式；
(2)若直线经过，两点，求直线的函数表达式；
(3)在抛物线的对称轴上找一点，使点到点的距离与到点的距离之和最小，求点的坐标；
(4)设点为抛物线的对称轴上的一个动点，求使为直角三角形的点的坐标．
参考答案与解析
1．B
【分析】本题考查了中心对称图形与轴对称图形，根据轴对称图形和中心对称图形的定义进行逐一判断即可：如果一个平面图形沿一条直线折叠，直线两旁的部分能够互相重合，这个图形就叫做轴对称图形；把一个图形绕着某一个点旋转，如果旋转后的图形能够与原来的图形重合，那么这个图形叫做中心对称图形，这个点就是它的对称中心．掌握中心对称图形与轴对称图形的判断是解题的关键．
【详解】解：A、是中心对称图形，但不是轴对称图形，故不符合题意；
B、既是轴对称图形，也是中心对称图形，故符合题意；
C、是轴对称图形，但不是中心对称图形，故不符合题意；
D、是轴对称图形，但不是中心对称图形，故不符合题意；
故选：B．
2．C
【分析】本题主要考查了概率公式和二次函数的图像性质，准确计算是解题的关键．
根据二次函数开口方向向下时，再根据概率计算公式计算即可；
【详解】∵抛物线开口向下，
∴，
∴在，，3中符合条件的是，，有2种情况，
∴使抛物线的开口向下的概率是．
故选C．
3．A
【分析】本题考查二次函数与一元二次方程的关系．根据抛物线与x轴有两个不同的交点，得到对应的方程有两个不相等的实数根，利用判别式求出a的取值范围即可，注意二次函数的二次项系数不能为0．
【详解】解：由题意，得：且，
∴且；
故选A．
4．B
【分析】本题考查了相似三角形的判定．根据有两组角对应相等的两个三角形相似对A进行判断；根据两组对应边的比相等且夹角对应相等的两个三角形相似对B进行判断；根据直角三角形相似的判定方法对C进行判断；根据三组对应边的比相等的两个三角形相似对D进行判断．
【详解】解：A、，，能判定，本选项不符合题意；
B、，，不能判定，本选项符合题意；
C、，，能判定，本选项不符合题意；
D、，能判定，本选项不符合题意；
故选：B．
5．B
【分析】先求出平移后的抛物线的顶点坐标，再利用顶点式抛物线解析式写出即可．
【详解】解：抛物线y=－2x2的顶点坐标为（0，0），
向左平移1个单位，再向下平移3个单位后的抛物线的顶点坐标为（－1，－3），
∴平移后的抛物线的解析式为y=－2（x+1）2－3．
故选：B．
【点睛】本题考查了二次函数图象与几何变换，要求熟练掌握平移的规律：左加右减，上加下减．并用根据规律利用顶点的变化确定函数解析式．
6．B
【分析】本题主要考查了比较二次函数值的大小，根据开口向上的二次函数，离对称轴越远，函数值越大，只需要比较出A、B、C三点离对称轴距离的大小即可得到答案．
【详解】解：∵二次函数解析式为，，
∴二次函数开口向上，对称轴为直线，
∴离对称轴越远，函数值越大，
∵，，为二次函数图象上的三点，，
∴．
故选：B．
7．B
【详解】试题分析：设母线长为R，底面半径为r，
∴底面周长=2πr，底面面积=πr2，侧面面积=πrR，
∵侧面积是底面积的2倍，
∴2πr2=πrR，
∴R=2r，
设圆心角为n，有=2πr=πR，
∴n=180°．
故选B．
考点：圆锥的计算
8．C
【分析】先利用切线长定理得到，再利用可判断为等边三角形，然后根据等边三角形的性质求解．
【详解】解：，PB为的切线，
，
，
为等边三角形，
．
故选C．
【点睛】本题考查切线长定理，掌握切线长定理是解题的关键．
9．C
【详解】解：如图，连接CD，
∵∠C=90°，D为AB的中点，
∴CD=DA=DB．
而CD=CB，
∴CD=CB=DB，即△CDB为等边三角形．
∴∠B=60°．
∵AB=10，
∴．
故选C．
10．B
【分析】过A点作AH⊥BC于H，利用等腰直角三角形的性质得到∠B=∠C=45°，BH=CH=AH= BC=2，分类讨论：当0≤x≤2时，如图1，易得PD=BD=x，根据三角形面积公式得到y=x2；当2＜x≤4时，如图2，易得PD=CD=4-x，根据三角形面积公式得到y=-x2+2x，于是可判断当0≤x≤2时，y与x的函数关系的图象为开口向上的抛物线的一部分，当2＜x≤4时，y与x的函数关系的图象为开口向下的抛物线的一部分，然后利用此特征可对四个选项进行判断．
【详解】解：过A点作AH⊥BC于H，
∵△ABC是等腰直角三角形，
∴∠B=∠C=45°，BH=CH=AH=BC=2，
当0≤x≤2时，如图1，∵∠B=45°，
∴PD=BD=x，
∴y=•x•x=；
当2＜x≤4时，如图2，∵∠C=45°，
∴PD=CD=4﹣x，
∴y=•（4﹣x）•x=，
故选B．
11．
【分析】本题考查二次函数的性质，直接利用对称轴的计算方法求解即可．
【详解】解：抛物线的对称轴是直线；
故答案为：．
12．
【分析】直接利用两个点关于原点对称时，它们的坐标符号相反，即点关于原点的对称点是，即可得出答案．
【详解】解：点与点关于原点对称，
，
，
故答案为：．
【点睛】本题主要考查了关于原点对称点的性质，正确记忆横纵坐标符号是解题的关键．
13．且
【分析】根据二次项系数非零及根的判别式，即可得出关于的一元一次不等式组，解之即可得出的取值范围．
【详解】∵关于的一元二次方程有实数解，
∴，
解得：且，
故答案为：且
【点睛】本题考查了根的判别式以及一元二次方程的定义，根据二次项系数非零及根的判别式，找出关于的一元一次不等式组是解题的关键．
14．##
【分析】此题主要考查了直角三角形内切圆的性质及半径的求法，勾股定理．根据已知得出是解题关键．
设、、与的切点分别为、、，证得四边形是正方形，然后根据切线长定理可得：，由此可求出半径的长，然后利用图中阴影部分的面积代数求解即可．
【详解】解：如图所示，设、、与的切点分别为、、

在，，，，
∴，
四边形中，，，
四边形是正方形，
由切线长定理，得：，，，
，
∴．
∴图中阴影部分的面积．
故答案为：．
15．60°
【分析】根据等边三角形的性质和旋转的性质即可求得答案.
【详解】解：∵△ABC是等边三角形，∴∠ABC=60°，
∵△BCM是由△BAP旋转所得，∴旋转中心是点B，旋转角为∠ABC=60°，
∴∠PBM=∠ABC=60°.
故答案为60°.
【点睛】本题考查了等边三角形的性质和旋转的性质，难度不大，掌握相关性质是解题的关键.
16．4
【分析】直接开平方求出的值，即可得到的值，舍去负数解即可．
【详解】解：，
∴或者，
∴，或者，
∵，
∴，
故答案为：4．
【点睛】本题考查开平方的运算，一个正数的有两个平方根，互为相反数，零的平方根是零，负数没有平方根，解题的关键是注意，舍去负数解．
17．20
【分析】设白球个数为x个，由摸到红球的频率稳定在0.2附近得出口袋中得到红色球的概率，然后根据概率公式列方程求解即可．
【详解】结：设白球个数为x个，
∵摸到红色球的频率稳定在0.2左右，
∴口袋中得到红色球的概率为0.2，
∴，解得：，
经检验是原方程的根，
故白球的个数为20个．
故答案为20．
【点睛】本题主要考查了利用频率估计概率，根据大量反复试验下频率稳定值即概率得出是解题关键．
18．①②④⑤
【分析】主要考查图象与二次函数系数之间的关系．根据抛物线开口方向、对称轴、与轴交点可判断①；根据抛物线与轴交点个数可判断②；根据与关于对称轴对称，且时，可判断③；根据时，，且对称轴为可判断④；由抛物线在时有最大值，可判断⑤．
【详解】解：①由抛物线图象得：；，，即，
，选项①正确；
②抛物线图象与轴有两个交点，
△，即，选项②正确；
③抛物线对称轴为，且时，，
当时，，即，选项③错误；
④抛物线对称轴，即，
，
由图象可知，当时，，
故，选项④正确；
⑤由图象可知，当时取得最大值，
，
，即，
，选项⑤正确；
故正确的有：①②④⑤，
故答案为：①②④⑤．
19．(1)
(2)，
【分析】（1）首先计算算术平方根，负整数指数幂和零指数幂，绝对值，然后计算加减；
（2）利用因式分解法解一元二次方程 ．
【详解】（1）
；
（2）
或
解得，．
【点睛】此题考查了算术平方根，负整数指数幂和零指数幂，绝对值的混合运算，解一元二次方程，解题的关键是熟练掌握以上运算法则．
20．（1）；（2）证明见解析
【分析】（1）直接把x=1代入方程求出m的值；
（2）计算出根的判别式，进一步利用配方法和非负数的性质证得结论即可．
【详解】解：（1）根据题意，将x=1代入方程，
得：，
解得：m=．
（2）∵，
∴不论m取何实数，该方程都有两个不相等的实数根．
【点睛】本题考查根的判别式，一元二次方程的解，熟记根的判别式与一元二次方程根的关系是解题的关键.
21．(1)图见解析，
(2)图见解析，
【分析】本题考查作图旋转变换，作图轴对称变换等知识，解题的关键是理解题意．
（1）利用轴对称的性质，分别作出、、关于轴对称点、、，顺次连接即可；
（2）利用旋转的性质，分别作出、、的对应点、、，顺次连接，求得的长，利用扇形的面积公式求解即可．
【详解】（1）解：如图所示，
，
故答案为：；
（2）解：如图所示；
，
∴所扫过的面积是．
故答案为：．
22．(1)40
(2)
【分析】本题考查了统计和随机抽样的概率；根据题意求出总人数、正确画出树状图并按照公式求解是解题的关键．
（1）根据A在频数统计图数据除以扇形统计图中的数据即可；
（2）画树状图，求出所有可能和符合条件数，根据概率公式求解即可．
【详解】（1）解：总人数为：（人）；
（2）画树状图如下：
从两男两女中随机抽取两名同学共有种可能，恰好抽到一名男生和一名女生有种可能，
恰好抽到一名男生和一名女生的概率为：．
23．(1)每张门票的原定票价为40元
(2)原定票价平均每次的降价率为
【分析】本题主要考查了一元二次方程和分式方程的应用，解题的关键是根据等量关系列出方程，注意要对分式方程的解进行检验．
（1）设每张门票的原定票价为元，则降价后的价格为元，根据按原定零售票价需花费2000元购买的门票，现在只花费了1200元，列出方程，解方程即可；
（2）设原定票价平均每次的降价率为，根据原定零售票价经过连续两次降价后票价为每张32.4元，列出方程，解方程即可．
【详解】（1）解：设每张门票的原定票价为元，则降价后的价格为元，
依题意，得：，
解得：，
经检验，是原方程的解，且符合题意．
答：每张门票的原定票价为40元．
（2）解：设原定票价平均每次的降价率为，
依题意，得：，
解得：，（不合题意，舍去）．
答：原定票价平均每次的降价率为．
24．(1)见解析
(2)
【分析】(1)由平行线的性质得出，，即可证得结论；
(2)由平行线的性质得出，易证△EFC∽△BAC，再由相似三角形的面积比等于相似比的平方，即可得出结果．
【详解】（1）证明：，
，
（2）解：



【点睛】本题考查了相似三角形的判定与性质、平行线的性质等知识；熟练掌握相似三角形的判定与性质是解题的关键．
25．(1)见解析
(2)
【分析】（1）连接，证明，得出，即可得出直线与相切；
（2）设半径为r，根据勾股定理得出，求出，根据，得出，根据勾股定理得出，求出结果即可．
【详解】（1）证明：连接，如图所示：
∵为切线，
∴，
又∵，
∴，，
，
∴，
在与中；
∵，
∴，
∴，
∴直线与相切．
（2）解：设半径为r，
在中，，
即，
解得；
，
，
在中，，
，
解得：．
【点睛】本题主要考查了勾股定理，三角形全等的判定和性质，等腰三角形的性质，切线的判定和性质，解题的关键是熟练掌握切线的判定方法．
26．(1)
(2)，见解析
(3)，
【分析】（1）根据已知条件利用边角边证明，再利用全等三角形的性质即可得到和的数量关系；
（2）根据任意等腰直角三角形的直角边与斜边的比是相等的，利用两边成比例且夹角相等的判定定理证明，之后再由相似三角形对应边成比例即可得到和的数量关系；
（3）连接，先由正方形的性质判断出和都是等腰直角三角形，再利用与第二问同样的方法证出，由相似比求出，再由勾股定理求得，则可列出关系式．
【详解】（1）解：是等腰直角三角形，，在中，，，
，，
．
在和中，
，
，
；
（2）解：，理由如下：
是等腰直角三角形，中，，，
，．
，
，
，
，
；
（3）解：连接，
四边形是正方形，四边形是正方形，
和都是等腰直角三角形，
，，
，
，
，
，
，，
，，
在中，，即，
是正方形的对角线，正方形的面积为，
，
，
，，
．
【点睛】本题是一道几何综合题，考查了正方形的性质，等腰直角三角形的性质，全等三角形的判定和性质，相似三角形的判定和性质，勾股定理，正确识图并能熟练地掌握几何图形的性质与判定定理进行证明是解题的关键．
27．(1)
(2)的函数表达式为
(3)
(4)的坐标为或或或
【分析】本题考查待定系数法求解函数解析式，二次函数的性质，两点之间线段最短，勾股定理；
（1）待定系数法求解析式，即可求解；
（2）根据对称性求得点的坐标，进而根据待定系数法求直线的解析式即可求解；
（3）设直线与对称轴的交点为，则此时的值最小，把代入直线即可求解；
（4）设，分别求得，进而分类讨论，根据勾股定理建立方程，即可求解．
【详解】（1）∵抛物线对称轴为，抛物线经过点，，
∴可得
解得：
∴抛物线解析式为．
（2）∵抛物线的对称轴为，且抛物线经过，
∴点的坐标为
∴把，分别代入直线，
得
解得：
∴直线的函数表达式为．
（3）设直线与对称轴的交点为，则此时的值最小
把代入直线得，
，
∴，
（4）设，
又∵，
∴，
，
，
①若点为直角顶点，则，
即：，
解之得：；
②若点为直角顶点，则，
即：，
解之得：，
③若点为直角顶点，则，
即：，
解之得：，
综上所述的坐标为或或或