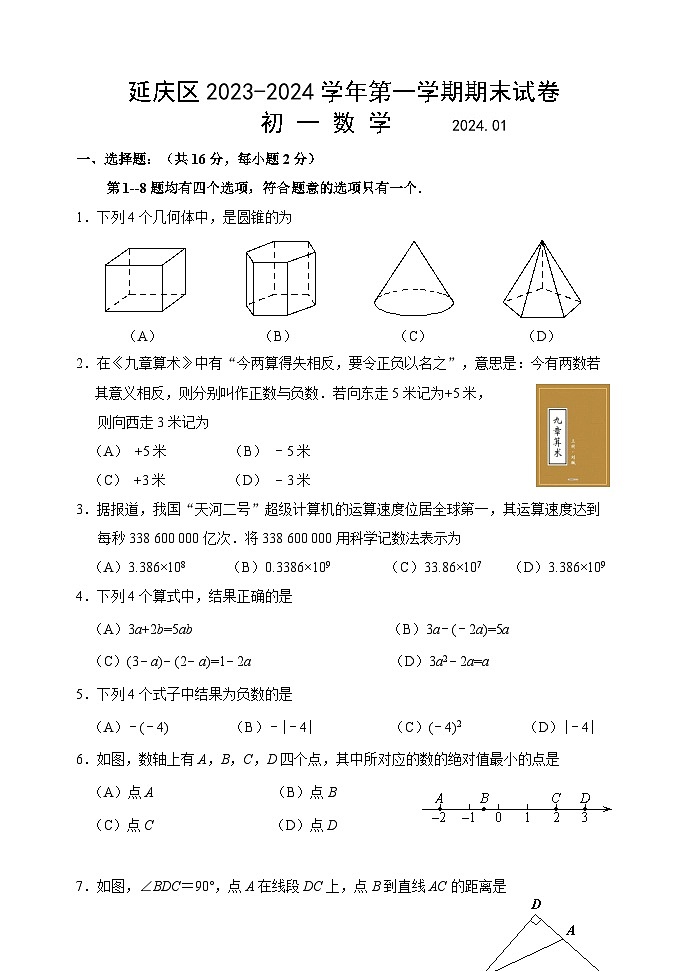
2023-2024学年北京市延庆区七年级第一学期期末数学试卷（含答案）

这是一份2023-2024学年北京市延庆区七年级第一学期期末数学试卷（含答案），共11页。


一、选择题：（共16分，每小题2分）
第1--8题均有四个选项，符合题意的选项只有一个．
1．下列4个几何体中，是圆锥的为
（A） （B） （C） （D）
2．在《九章算术》中有“今两算得失相反，要令正负以名之”，意思是：今有两数若
其意义相反，则分别叫作正数与负数．若向东走5米记为+5米，
则向西走3米记为
（A） +5米 （B） 5米
（C） +3米 （D） 3米
3．据报道，我国“天河二号”超级计算机的运算速度位居全球第一，其运算速度达到
每秒338 600 000亿次．将338 600 000用科学记数法表示为
（A）3.386×108 （B）0.3386×109 （C）33.86×107 （D）3.386×109
4．下列4个算式中，结果正确的是
（A）3a+2b=5ab （B）3a(2a)=5a
（C）(3a)(2a)=12a （D）3a22a=a
5．下列4个式子中结果为负数的是
（A）(4) （B）|4| （C）(4)2 （D）|4|
6．如图，数轴上有A，B，C，D四个点，其中所对应的数的绝对值最小的点是
（A）点A （B）点B
（C）点C （D）点D
7．如图，∠BDC＝90°，点A在线段DC上，点B到直线AC的距离是
（A）线段DA的长 （B）线段BA的长
（C）线段DC的长 （D）线段BD的长
8．下列说法：
①单项式ab2的系数是1；②单项式ab2的次数是2；③多项式a+b2的次数是3．
正确的是
（A）① （B）② （C）③ （D）①②③
二、填空题 （共16分，每小题2分）
9．4的相反数是 ．
10．写出一个大于5的负整数是 ．
11．比较大小：3 2（填“＞”，“＜”或“=”）．
12．如果x=3是关于x的方程2x+3a=18的解，那么a的值是 ．
13．如果单项式3x2my6与5x4yn+3是同类项，那么nm的值是 ．
14．计算：90°50°30′= ．
15．我国明代著名数学家程大位的《算法统宗》一书中记载了一个“百羊问题”：甲赶群羊逐草茂，乙拽肥羊一只随其后；戏问甲及一百否？甲云所说无差谬，若得这般一群凑，再添半群小半群，得你一只来方凑，玄机奥妙谁猜透．题目的意思是：甲赶了一群羊在草地上往前走，乙牵了一只肥羊紧跟在甲的后面．乙问甲：“你这群羊有一百只吗？”甲说：“如果再有这么一群，再加半群，又加四分之一群，再把你的一只凑进来，才满100只．”请问甲赶的羊一共有多少只？如果设甲赶的羊一共有x只，那么可列方程为 ．
16．下面的框图是解方程的流程：
4(5y+4)+3(y1)=24(5y5)
20y +16+3y3=245y +5
28y =16
③ 移项
④ 合并同类项
⑤ 系数化为1
① 去分母
② 去括号
20y +3y +5y =24+516+3
在上述五个步骤中，依据是“等式的基本性质2”的步骤有 ．（只填序号）
三、解答题（17-18题，每小题8分；19-26题，每小题5分；27-28题，每小题6分）
17．计算： （1）(5) +9(6)20； （2）10÷ (2)+ (7)×(3)(4)．
18．计算： （1）； （2）.
19．解方程： 2x3= x +1．
20．解方程：．
21．先化简，再求值：
已知：，其中，．
22．已知：点C是线段AB的中点，点D在直线AB上，且BC =5，BD =3．
（1）求线段AB的长；
（2）直接写出线段AD的长．
23．按要求画图：
如图，点A，B，C，D是同一平面内的四个点．
（1）画线段AB和直线AC；
（2）在线段AB的反向延长线上取一点E，使EA =AB；
（3）过点D作DF⊥AB于点F；
（4）在直线AC上找一点P，使得EP＋PD最小．
24．如图，∠CAB+∠ABC=90°，AD平分∠CAB，交BC边于点D，BE平分∠ABC，交AC边于点E．
（1）依题意补全图形；
（2）①∠DAB+∠EBA= °；
②补全证明过程．
证明：∵ AD平分∠CAB，BE平分∠ABC，
∴ ∠DAB=∠CAB，
∠EBA= ．
（理由： ）
∵∠CAB+∠ABC=90°，
∴∠DAB+∠EBA=(∠CAB+∠ABC)=_____．
25. 本学期学习了一元一次方程的解法，下面是小明同学的解题过程：
解方程：．
…………第一步
解：原方程可化为：．
…………第二步
方程两边同时乘以15，去分母，得
3(20x3)5(10x +4)=15．
…………第三步
去括号，得 60x950x +20=15．
………第四步
移项，得 60x50x=15+920．
…………第五步
合并同类项，得 10x=4．
…………第六步
系数化1，得 x=0.4．
所以x=0.4是原方程的解．
上述小明的解题过程从第 步开始出现错误，
错误的原因是________________________________________________．
请你写出正确的解题过程．
26．列方程解应用题：
延庆区张山营镇是著名的“苹果之乡”，出产的苹果色泽鲜艳、品种优良，红富士苹果获得“中华名果”的称号．秋收季节，某公司打算到张山营果园基地购买一批苹果．果园基地对购买量在1000千克（含1000千克）以上的有两种销售方案，方案一：每千克10元，由基地送货上门；方案二：每千克8元，由顾客自己运回．已知该公司租车从基地到公司的运输费为5000元．
（1）公司购买多少千克苹果时，选择两种购买方案所需的费用相同？
（2）如果公司打算购买3000千克苹果，选择哪种方案省钱？为什么？
27．阅读材料：
对于任意有理数a，b，规定一种特别的运算“”：ab= ab+ab．
例如，25=25+2×5=7．
（1）求3(1) 的值；
（2）若(4)x=6，求x的值；
（3）试探究这种特别的运算“”是否具有交换律？
28．对于数轴上三个不同的点A，B，C，给出如下定义：在线段AB，BC，CA中，若其中有两条线段相等，则称A，B，C三点是“均衡点”．
（1）点A表示的数是2，点B表示的数是1，点C表示的数是3，
① A，B，C三点______（填“是”或“不是”）“均衡点”；
②点M表示的数是m，且B，C，M三点是“均衡点”，则m= ；
（2）点D表示的数是x，点E表示的数是n，线段EF=a（a为正整数），线段
DE=b，若D，E，F三点是“均衡点”，且关于x的一元一次方程ax+x=4b的
解为整数，求n的最小值．
延庆区2023-2024学年第一学期期末试卷答案
初 一 数 学 2024.01
一、选择题：（共8个小题，每小题2分，共16分）
CDAB BBDA
二、填空题：（共8个小题，每小题2分，共16分）
9．4 10．答案不唯一 11．＜ 12．4
13．9 14．39°30′ 15． 16．①⑤
三、解答题
17．（本小题满分8分）
(1)原式=5+9+620
……………………4分
=25+15
=10．
(2)原式=5+21+4
……………………4分
=5+25
=20．
18．（本小题满分8分）
(1)原式
……………………4分
=12+159
=6．
(2)
……………………4分
=1+1
=0．
19．（本小题满分5分）
解：2xx = 1+3
……………………5分
x= 4．
20．（本小题满分5分）
解：


……………………5分
．
21．（本小题满分5分）
解：原式


当，时，原式
……………………5分
．
22．（本小题满分5分）
(1)解：∵点C是线段AB的中点（已知），
∴AB = 2BC（线段中点的定义）．
∵BC =5，
……………………5分
∴AB =10．
(2) AD =13或者AD =7．
23．（本小题满分5分）

……………………5分

24．（本小题满分5分）
(1)如图；
……………………5分
(2)，，角平分线定义，．
25．（本小题满分5分）
从第三步出错，错误原因是：略．
解：原方程可化为：．
方程两边同时乘以15，去分母，得
3(20x3)5(10x +4)=15．
去括号，得 60x950x20=15．
移项，得 60x50x=15+9+20．
合并同类项，得 10x=44．
系数化1，得 x=4.4．
……………………5分
所以x=4.4是原方程的解．
26．（本小题满分5分）
解：(1)设公司购买x千克苹果时，选择两种购买方案所需费用相同.
根据题意，得：．
解得：
答：公司购买千克苹果时，选择两种购买方案所需费用相同．
(2)当时，
……………………5分
∵30000>29000，
∴选择方案二省钱．
27．（本小题满分6分）
解：(1)3(1)=3(1)+3×(1)=1；
(2)∵(4)x=6，
∴(4)x+(4)×x=6
x=2．
(3)不具有交换律．
答案不唯一，例如：
∵ 3(1)=3(1)+3×(1)=1，
(1)3=(1)3+(1)×3=7，
……………………6分
∴3(1) ≠ (1)3．
∴不具有交换律．
28．（本小题满分6分）
……………………4分
(1)①不是；
②1,2,5；
(2) 7．
更多初中数学资料，初中数学试题精解
请微信关注