贵州省黔东南苗族侗族自治州三穗中学2024-2025学年上学期八年级期中模拟数学试卷

这是一份贵州省黔东南苗族侗族自治州三穗中学2024-2025学年上学期八年级期中模拟数学试卷，共8页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
八（ ）班 学号 姓名 成绩
一、选择题（每小题3分，共36分）
第3题图
1.下列图形中，轴对称图形的个数是（ ）
A.1个 B.2个 C.3个 D.4个
第5题图
2.已知三角形两边长分别为4和9，第三边为奇数，则该三角形第三边的长可能是（ ）
A.5 B.10 C.11 D.12
如图，在四边形ABCD中，AB＝CD，AD＝BC，E，F是对角线BD上的两点.若添加一
个条件使△ABE≌△CDF，则添加的条件不能是 （ ）
A.AE＝CF B.BE＝DF C.∠1＝∠2 D.∠AEB＝∠CFD
第6题图
4.在△ABC中，AB=AC， D为BC的中点，有下列四个结论：①∠B=∠C；②AD⊥BC；
③∠BAC=2∠BAD；④S△ABD=S△ACD，其中正确的有 （ ）
A.1个 B.2个 C.3个 D.4个
5.如图,五角星的五个角都是顶角为360的等腰三角形，则∠AMB的度数为（ ）
A.1440 B.1200 C.1080 D.1000
第7题
6.如图，Rt△ABC中，∠C=900，∠B=300，分别以点A和点B为圆心，大于AB的长为半径画弧，两弧相交于M，N两点，作直线MN，交BC于点D，连接AD，则∠CAD的度数是（ ）
A.200 B.300 C.450 D.600
7.如图，在△ABC中，∠C=，DE是AB的垂直平分线，AD恰好
平分∠BAC.若DE=3,则BC的长是（ ）
第8题图
A.9 B.6 C.7 D. 5
8.如图，在△ABC中,∠ABC、∠ACB的平分线相交于点F，过点F作DE∥BC，交AB于
点D,交AC于点E，则下列结论中正确的有：（1）△BDF、△CEF都是等腰三角形；
（2）DE=DB＋CE；（3）BF=CF； (4)AD＋DE＋AE=AB＋AC；正确的有（ ）
第9题图
A.1个 B.2个 C.3个 D.4个
9.如图，等边△ABC的边长为6，动点P、Q分别从A、B两点出发，沿AB、BC方
向匀速运动，它们的速度都是1厘米/秒，当点P到达B点时，P、Q两点停止运动，
设P、Q两点运动的时间为秒，若△PBQ为直角三角形时，则的值是（ ）
A.2秒 B.4秒 C.2秒或4秒 D.3秒
11题图
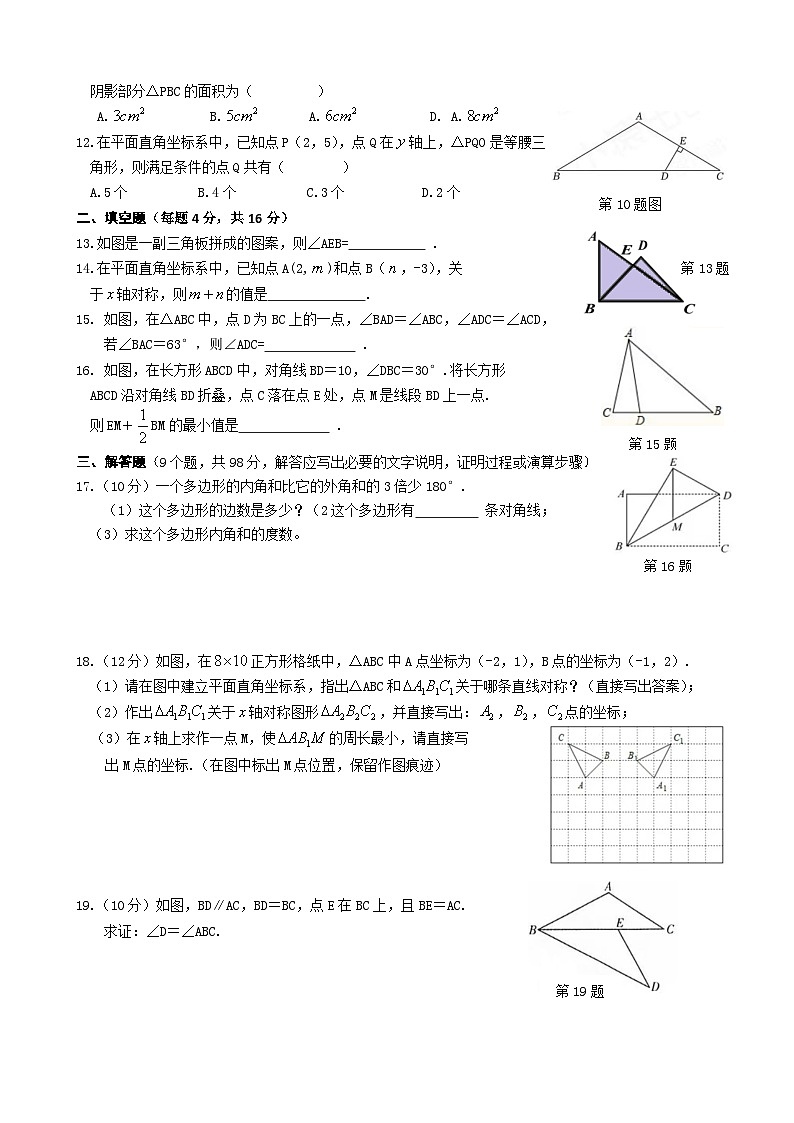
10.如图，已知在△ABC中，AB＝AC，∠A＝120°，DE垂直平分AC，若CD＝2，
则BD的长为（ ）
A.3 B.4 C.5 D.6
如图，△ABC的面积为10,AP垂直于∠B的平分线BP于P，则
阴影部分△PBC的面积为（ ）
第10题图
A. B. A. D. A.
12.在平面直角坐标系中，已知点P（2，5），点Q在轴上，△PQO是等腰三
角形，则满足条件的点Q共有（ ）
A.5个 B.4个 C.3个 D.2个
二、填空题（每题4分，共16分）
第13题
13.如图是一副三角板拼成的图案，则∠AEB= .
14.在平面直角坐标系中，已知点A(2,)和点B（，-3），关
于轴对称，则的值是 .
第15题
如图，在△ABC中，点D为BC上的一点，∠BAD＝∠ABC，∠ADC＝∠ACD，
若∠BAC＝63°，则∠ADC= .
如图，在长方形ABCD中，对角线BD＝10，∠DBC＝30°.将长方形
ABCD沿对角线BD折叠，点C落在点E处，点M是线段BD上一点.
则EM＋BM的最小值是 .
第16题
三、解答题（9个题，共98分，解答应写出必要的文字说明，证明过程或演算步骤）
17.（10分）一个多边形的内角和比它的外角和的3倍少180°.
这个多边形的边数是多少？（2这个多边形有 条对角线；
（3）求这个多边形内角和的度数。
18.（12分）如图，在正方形格纸中，△ABC中A点坐标为（-2，1），B点的坐标为（-1，2）.
（1）请在图中建立平面直角坐标系，指出△ABC和关于哪条直线对称？（直接写出答案）；
（2）作出关于轴对称图形，并直接写出：，，点的坐标；
（3）在轴上求作一点M，使的周长最小，请直接写
出M点的坐标.（在图中标出M点位置，保留作图痕迹）
第19题
19.（10分）如图，BD∥AC，BD＝BC，点E在BC上，且BE＝AC.
求证：∠D＝∠ABC.
第20题图
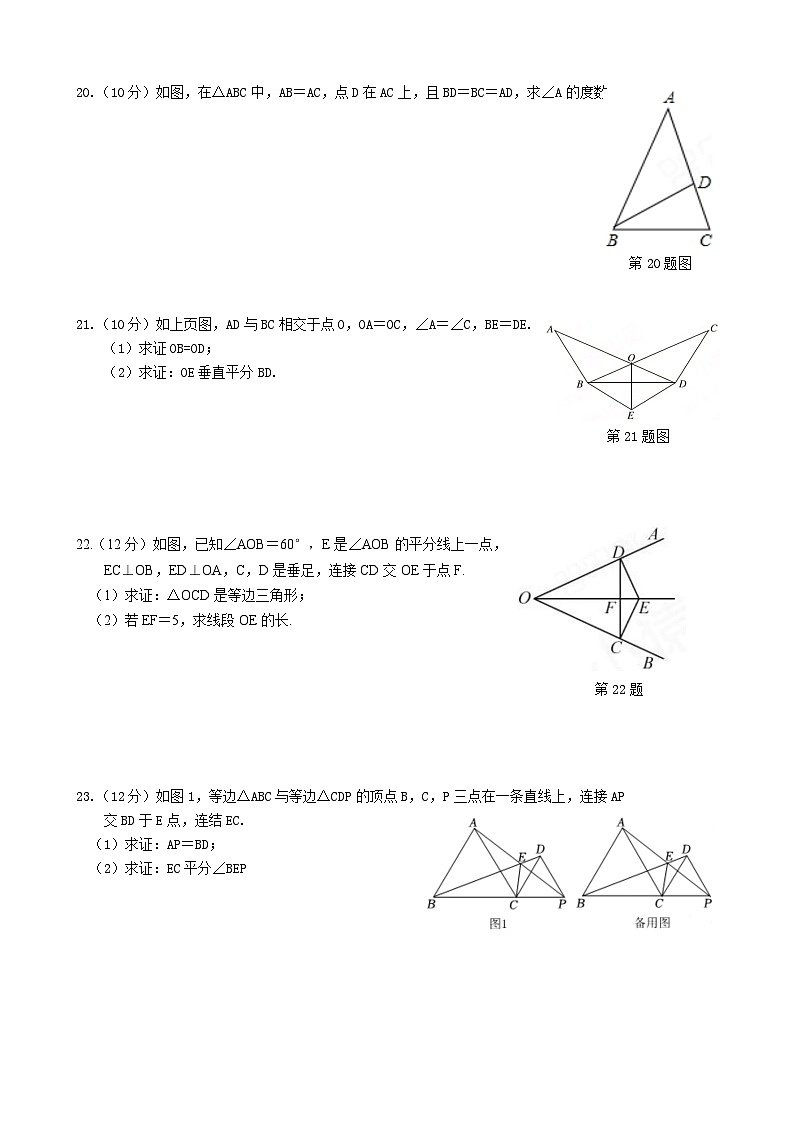
20.（10分）如图，在△ABC中，AB＝AC，点D在AC上，且BD＝BC＝AD，求∠A的度数.
第21题图
21.（10分）如上页图，AD与BC相交于点O，OA＝OC，∠A＝∠C，BE＝DE.
（1）求证OB=OD；
（2）求证：OE垂直平分BD.
第22题
22.（12分）如图，已知∠AOB＝60°，E是∠AOB的平分线上一点，
EC⊥OB，ED⊥OA，C，D是垂足，连接CD交OE于点F.
（1）求证：△OCD是等边三角形；
（2）若EF＝5，求线段OE的长.
23.（12分）如图1，等边△ABC与等边△CDP的顶点B，C，P三点在一条直线上，连接AP
交BD于E点，连结EC.
（1）求证：AP＝BD；
（2）求证：EC平分∠BEP
24.（12分）如图，△ABC是边长为6的等边三角形，P是AC边上一动点，由点A向点C运动（点P与点
A，C不重合），Q是CB的延长线上一点，与点P同时以相同的速度由点B向CB的延长线方向运动（点Q不与点B重合），连接PQ，交AB于点D.
（1）当∠BQD＝30°时，求AP的长；
（2）求证：在运动过程中，D是线段PQ的中点（提示：作PF∥BC）.
25.（14分）数学是一个允满乐趣、奥妙，又极具探索的学科，对一个人的思维也是一种“挑战”，几何图形更是变幻无穷，但只要我们借助图形的直观、特殊情形出发，逐步“从特殊到一般”进行探索，思路和方法自然就会显现出来.下面是一道探索几何图形中线段AE与DB数量关系的例子：在等边三角形ABC 中，点E在AB上，点D在CB的延长线上，且ED＝EC.小张的思路是：
（1）【特殊探索】如图①，当E为AB的中点时，确定线段AE和DB的大小关系，请你直接写出结论：AE“＜”或“＝”）DB；
【特例引路】如图②，当E为AB边上任意一点时，确定线段AE与DB的大小关系，请你直接写出结
论：AE“＞”“＜”或“＝”）DB；理由如下：过点E作EF∥BC交AC于点F；（请你将接下来的解答过程补充完整）
【拓展延伸】在等边△ABC中，点E在AB边的延长线上，点D在CB边的延长线上，且ED＝EC，若
△ABC的边长为1，AE＝2，求CD的长.（请你画出相应图形，并简要写出求CD长的过程）
③
三穗中学2024-2025学年度第一学期期中考试八年级数学模拟试卷
参 考 答 案
一、选择题：(每题3分，共36分）
二、填空题：（每题4分，共16分）
13. 75°； 14. 5 ； 15. 78°； 16. 7.5
三、解答题：（本题9个小题，共98分）
17.（10分）解：（1）设这个多边形的边数为n，则
（n-2）×180=360×3-180……（3分）
解得n=7
∴这个多边形的边数是7……（5分）
（2）14；分
（3）
答：这个多边形的内角和为分
18.（10分）解：（1）关于轴；分
（2）A2（2，-1），B2（1，-2），C2（3，-3），……（4分）；作图正确……（6分）；
（3）作图正确分；
第19题
M（-1，0）分
（10分）证明：∵BD∥AC，
∴∠ACB＝∠分
在△ABC和△EDB中，
∴△ABC≌△EDB（SAS）分
∴∠D=∠分.
20.（10分）解：设∠A＝分
∵BD＝AD，
∴∠A＝∠ABD＝分
∠BDC＝∠A＋∠ABD＝分
∵BD＝BC，
∴∠BDC＝∠BCD＝分
∵AB＝AC，
∴∠ABC＝∠BCD＝分
在△ABC中，＋2＋2＝180°，
解得：＝36，分
∴∠ABC＝2=72°.。分.
第21题图
21.（10分）证明：（1）在△AOB与△COD中，

∴△AOB≌△COD（ASA），分
∴OB＝分.
（2）∵OB＝OD，
∴点O在线段BD的垂直平分线上分
又 BE＝DE.
∴点E在线段BD的垂直平分线上分
∴OE垂直平分BD.。分.
22.（12分）（1）证明：∵点E是∠AOB的平分线上一点，EC⊥OB，ED⊥OA，
∴DE＝CE，∠ODE＝∠OCE＝90°分
第22题
在Rt△ODE 与 Rt△OCE 中，
∴Rt△ODE ≌ Rt△OCE（HL）分
∴OD＝分
∵∠AOB＝60°，
∴△OCD 是等边三角形分
解：由（1）知△OCD是等边三角形，OF是∠COD的平分线，
∴∠DOC＝∠ODC＝∠OCD＝60°，∠AOE＝∠BOE＝30°分
∴∠OFD＝90°分
∵∠ODE＝90°
∴∠EDF＝30°分
∴DE＝2EF＝分
∴OE＝2DE＝分.
23.（12分）（1）证明：∵△ABC与△CDP都是等边三角形，
∴∠ACB＝∠DCP＝60°，AC=AB，CD=CP，分
∴∠ACB+∠ACD=∠DCP＋∠ACD
∴∠BCD＝∠ACP，分
在△BCD与△ACP中，
∴△BCD≌△ACP（SAS）分
∴ AP＝ 分
（2）证明：如图2，过点C作CM⊥BD交BD于点M，过点C作CN⊥AP交AP于点N，
∴∠ANC=∠BMC=90°分
图2
又∵△BCD≌△ACP（SAS），
∴∠CBM ＝∠CAN，分
在△ANC和△BMC中，
∴△ANC≌△BMC（SAS）分
∴ CM＝CN，分
∴EC平分∠分
（12分）解：设AP＝，由题意，得AP＝BQ＝.
∵等边△ABC，
∴AC＝BC＝6，∠C＝60°＝∠A＝∠分
∴CQ＝6＋，CP＝6-分
∵∠CPQ＝180°-∠C-∠BQD＝90°，∠BQD＝30°，
∴QC＝2PC.即6＋＝2（6-）.
解得＝2，分
∴AP＝2；分
F
证明：过点P作PF∥BC交AB于F，则
∠AFP＝∠ABC＝60°，∠APF＝∠C＝60°，∠FPD＝∠BQD.
∴△APF是等边三角形，分
∴PF＝AP＝分
在△PFD和△BQD中，
∴△FPD≌△BQD（AAS）
∴PD＝DQ，
即D是PQ的中点分
（12分）解：（1）AE=DB；分.
（2）AE=分
证明：∵△ABC为等边三角形，
∴∠A=∠ABC=∠ACB=600；AB=AC
∴∠DBE=1200.
又EF∥BC，
∠AEF=∠ABC ，∠AFE=∠ACB=600，
∴∠A=∠AEF=∠AFE=600，∠EFC=1200.
∴△AEF为等边三角形，∠DBE=∠分
∴AE＝EF，
∵ED＝EC，
∴∠D＝∠ECD.
∵∠DEB＝60°-∠D，∠ECF＝60°-∠ECD，
∴∠DEB＝∠分
在△DBE和△EFC中，
∴△DBE≌△EFC（SAS），
∴DB＝EF，
∴AE＝分
（3）解：过EF作EF∥BC
∴∠ABC=∠AEF，∠ACB=∠F，∠ECD=∠CEF，
∵△ABC为等边三角形，
③
∴∠A=∠ABC=∠ACB=600.
∴∠A=∠AEF=∠AFE=600.∠DBE=∠ABC=600.
D
∴△AEF为等边三角形，∠DBE=∠AFE
∴EF=AE=AF=2，BE=BC=CF=1.
F
E
又DE=CE，
∴∠D=∠ECD
∴∠D=∠CEF，分
在△DBE和△EFC中，
∴△DBE≌△EFC（AAS），
∴DB=EF=2
∴CD=2+1=分.
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
B
C
A
D
C
B
A
C
C
B
B
B