山东省济宁市梁山县2024--2025学年上学期期中教学质量监测九年级数学试题

这是一份山东省济宁市梁山县2024--2025学年上学期期中教学质量监测九年级数学试题，共11页。试卷主要包含了请将答案正确填写在答题卡上，风力发电机可以在风力作用下发电，函数的图象可能是下列图象中的等内容，欢迎下载使用。
注意事项：
友情提示：亲爱的同学，这份试卷将展示你的学识与才华，记录你的智慧与收获．相信你独特的思考、个性化的体验、富有创意的表达一定是最棒的！
你将要解答的这份试题分为第Ⅰ卷和第Ⅱ卷两部分，第Ⅰ卷为选择题，36分，第Ⅱ卷为非选择题，84分，试题满分120分，考试时间为120分钟．
第Ⅰ卷每小题选出答案后，必须用2B铅笔把答题卡上对应题目的答案标号（ABCD）涂黑．如需改动，须先用橡皮擦干净，再涂改其他答案，第Ⅱ卷在答题卡上作答，答题时按照题目顺序在各题目的答题区域内作答．考试时，不允许使用计算器．
另外，答题前请务必在答题卡及试卷的规定位置将自己的姓名、考试号、考试科目、座号等填写（涂）准确吆！2．请将答案正确填写在答题卡上
第Ⅰ卷（选择题共36分）
一、精心选一选，相信自己的判断力！（本题共36小题，每小题3分）注意可以用各种不同的方法来解决你面前的选择题哦！
1．在平面直角坐标系中，点与点B关于原点对称，则点B的坐标为（ ）
A．B．C．D．
2．若是方程的一个根，则a的值是（ ）
A．B．C．D．
3．在下列二次函数中，其图象对称轴为直线的是（ ）
A．B．C．D．
4．数学世界奇妙无穷，其中曲线是微分几何的研究对象之一，下列数学曲线既是轴对称图形，又是中心对称图形的是（ ）
A．B．C．D．
5．小明在半径为5的圆中测量弦的长度，下列测量结果中一定是错误的是（ ）
A．4B．5C．10D．11
6．用配方法解方程，变形后的结果正确的是（ ）
A．B．C．D．
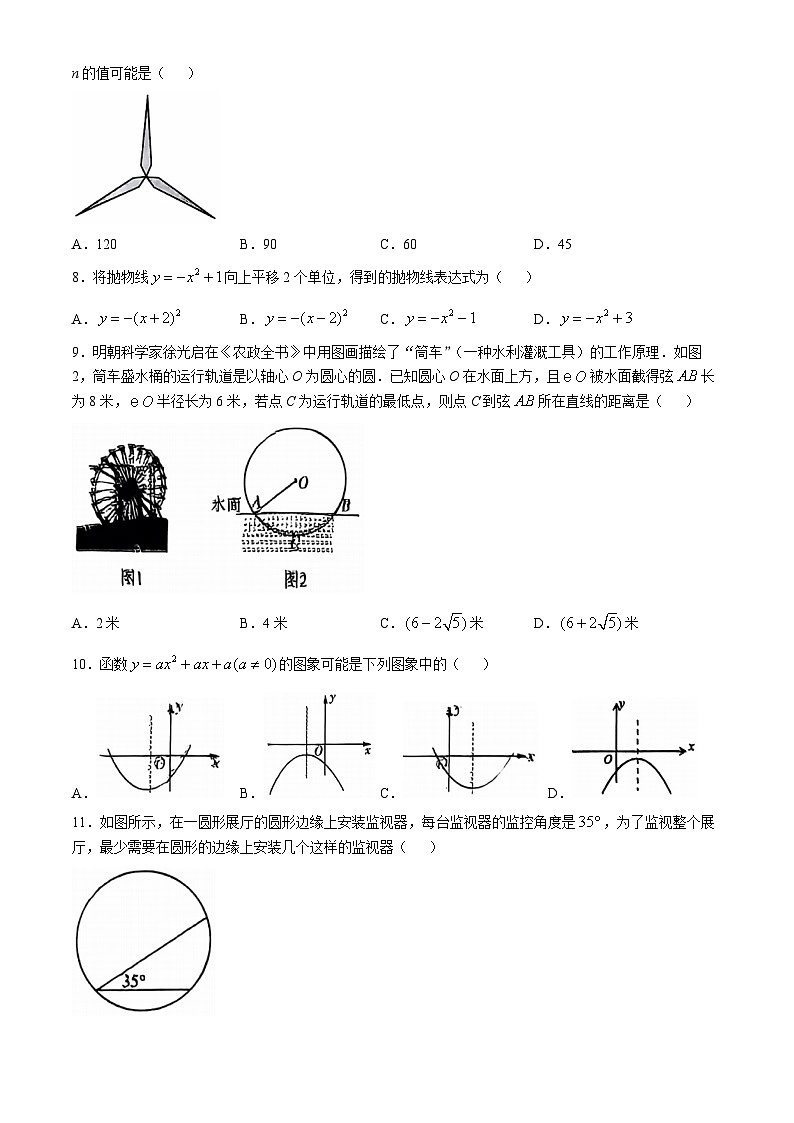
7．风力发电机可以在风力作用下发电．如图的转子叶片图案绕中心旋转后能与原来的图案重合，那么n的值可能是（ ）
A．120B．90C．60D．45
8．将抛物线向上平移2个单位，得到的抛物线表达式为（ ）
A．B．C．D．
9．明朝科学家徐光启在《农政全书》中用图画描绘了“筒车”（一种水利灌溉工具）的工作原理．如图2，筒车盛水桶的运行轨道是以轴心O为圆心的圆．已知圆心O在水面上方，且被水面截得弦长为8米，半径长为6米，若点C为运行轨道的最低点，则点C到弦所在直线的距离是（ ）
A．2米B．4米C．米D．米
10．函数的图象可能是下列图象中的（ ）
A．B．C．D．
11．如图所示，在一圆形展厅的圆形边缘上安装监视器，每台监视器的监控角度是，为了监视整个展厅，最少需要在圆形的边缘上安装几个这样的监视器（ ）
A．4台B．5台C．6台D．7台
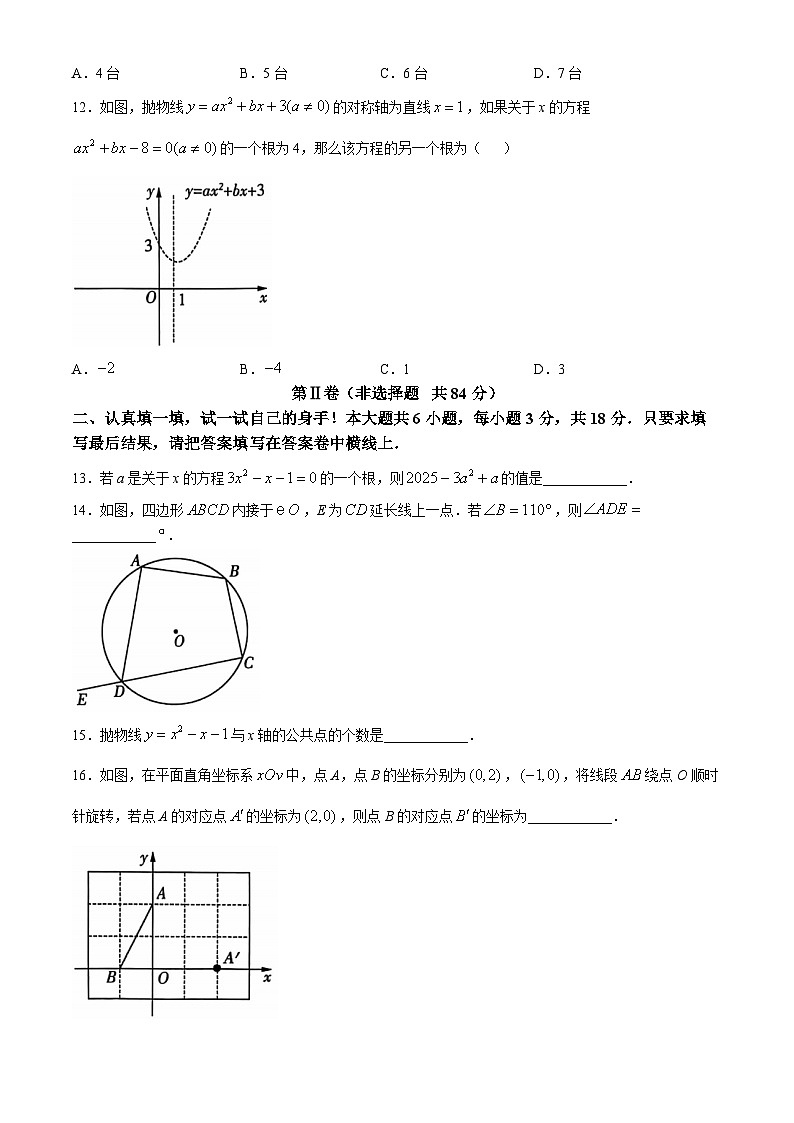
12．如图，抛物线的对称轴为直线，如果关于x的方程的一个根为4，那么该方程的另一个根为（ ）
A．B．C．1D．3
第Ⅱ卷（非选择题共84分）
二、认真填一填，试一试自己的身手！本大题共6小题，每小题3分，共18分．只要求填写最后结果，请把答案填写在答案卷中横线上．
13．若a是关于x的方程的一个根，则的值是____________．
14．如图，四边形内接于，E为延长线上一点．若，则____________．
15．抛物线与x轴的公共点的个数是____________．
16．如图，在平面直角坐标系中，点A，点B的坐标分别为，，将线段绕点O顺时针旋转，若点A的对应点的坐标为，则点B的对应点的坐标为____________．
17．已知抛物线经过点，，则____________（填“”，“”，“”）
18．如图，在中，，，．将沿x轴依次以点A，B，O为旋转中心顺时针旋转，分别得到图②、图③…．则旋转得到的第7个三角形的直角顶点的坐标为____________．
三、解答题
19．（本题满分6分）解下列方程：
（1）；
（2）．
20．（本题满分9分）阅读下列材料：
解方程：．这是一个一元四次方程，根据该方程的特点，它的解法通常是：
设，那么，于是原方程可变为①，
解这个方程得：，．
当时，，∴；
当时，，∴，
所以原方程有四个根：，，，．
在这个过程中，我们利用换元法达到降次的目的，体现了转化的数学思想．
（1）解方程时，若设，则原方程可转化为____________；
（2）若，求____________；
（3）参照上面解题的思想方法解方程：．
21．（本题满分8分）
已知二次函数（a，b是常数，且）的图象过，交y轴于点B．
（1）求点B的坐标及二次函数图象的对称轴．
（2）若该函数图象的顶点在直线上，求该函数的表达式．
22．（本题满分7分）如图，的半径，是弦，C是上一点，且，．求的度数．
23．（本题满分8分）如图，在平面直角坐标系中，已知的三个顶点的坐标分别为，，．
（1）将绕原点O逆时针旋转，画出旋转后的图形；
（2）的面积为____________；
（3）D点在平面内，且以A，B，C，D为顶点的四边形是平行四边形，则D点的坐标为____________．
24．（本题满分8分）“我运动，我健康，我快乐！”随着人们对身心健康的关注度越来越高．某市参加健身运动的人数逐年增多，从2021年的32万人增加到2023年的50万人．
（1）求该市参加健身运动人数的年均增长率；
（2）为支持市民的健身运动，市政府决定从A公司购买某种套装健身器材．该公司规定：若购买不超过100套，每套售价1600元；若超过100套，每增加10套，售价每套可降低40元．但最低售价不得少于1000元．已知市政府向该公司支付货款24万元，求购买的这种健身器材的套数．
25．（本题满分9分）如图，为锐角的外接圆，半径为5．
（1）用尺规作图作出的平分线，并标出它与劣弧的交点E（保留作图痕迹，不写作法）；
（2）若（1）中的点E到弦的距离为3，求弦的长．
26．（本题满分11分）如图，抛物线经过，两点，与x轴交于另一点B，连接，．
（1）求抛物线的解析式；
（2）平行于x轴的直线与抛物线分别交于点D，E，求线段的长．
（3）点P是线段上一点（不与点B，O重合），过点P作轴交抛物线于点M，连接，，求面积的最大值，及此时点M坐标．
九年级数学参考答案
一、选择题（共12小题，每小题3分，共36分）
1．B2．A3．D4．C5．D6．B7．A8．D9．C10．B
11．C12．A
二、填空题（本大题共6小题，每小题3分，共18分）
13．202414．11015．216．17．18．
三、解答题（本大题共8小题，共66分）
19．（本题满分6分）
（1）解：（1），
，1分
∴或，
∴，；3分
（2）
，
∴或，4分
∴，．6分
20．（本题满分9分）
解：（1）；2分
（2）44分
（3）
设，则，5分
原方程变形为：，
，
，
解得：，7分
∴，
去分母得：
解得：，，
经检验，和是上述分式方程的根，
∴原方程的解为：，．9分
21．（本题满分8分）
解：（1）由题意，∵二次函数交y轴于点B．
又当时，，
∴．2分
由∵，
∴对称轴是直线．4分
（2）由题意，根据（1）对称粒是直线，
∴抛物线的顶点为．
又∵顶点在直线上，
∴．
又∵在抛物线上，
∴．
∴，．
∴抛物线为．8分
22．（本题满分7分）
解：连接，1分
∵，
∴，
∵，
∴，
∴，
∵，
∴，
∴，即，
∴．7分
23．（本题满分8分）
解：（1）如图1，就是求作的三角形；
3分
（2）；5分
（3）D点的坐标为或或．8分
24．（本题满分8分）
解：（1）设该市参加健身运动人数的年均增长率为x，
由题意得：，
解得：，（不符合题意，舍去），
答：该市参加健身运动人数的年均增长率为；4分
（2）设购买的这种健身器材的套数为m套，
由题意得：，
整理得：，
解得：，（不符合题意，舍去）．
答：购买的这种健身器材的套数为200套．8分
25．（本题满分9分）
解：（1）如图，为所作；
4分
（2）连接交于F，连接，，如图，
∵平分，
∴，
∴，
∴，
∴，
∴，
在中，，7分
在中，．9分
26．（本题满分11分）
解：（1），解得：．1分
则抛物线的表达式为：，
将点A的坐标代入上式得，，
解得：，2分
故抛物线的表达式为：；3分
（2）∵平行于x轴的直线与抛物线分别交于点D，E，
∴，
解得或，5分
∴，，
∴；6分
（3）∵抛物线与x轴交于A，B，
∴，7分
设直线的解析式为，
，
∴，
∴直线的解析式为．8分
如图，直线交于点N，
设，则，，
∴，9分
∴
，10分
∴
，
∴当时，的面积最大，最大值为8．
此时点M坐标为．11分