

辽宁省辽阳市灯塔市2024-2025学年九年级上学期11月期中考试数学试题
展开
这是一份辽宁省辽阳市灯塔市2024-2025学年九年级上学期11月期中考试数学试题,共13页。试卷主要包含了答题前,考生须用0,证明等内容,欢迎下载使用。
注意事项:
1.答题前,考生须用0.5mm黑色字迹的签字笔在本试题卷规定位置填写自己的姓名、准考证号;
2.考生须在答题卡上作答,不能在本试题卷上作答,答在本试题卷上无效;
3.考试结束,将答题卡交回,进行统一评卷;
选择题(每题3分,共30分)
1.下列图形中,既是轴对称图形,又是中心对称图形的是( )
A.B.
C.D.
2.要使方程(a﹣5)x2+(b+1)x+c=0是关于x的一元二次方程,则( )
A.a≠0B.a≠5
C.a≠1且b≠﹣1D.a≠5且b≠﹣1且c≠0
3.下列命题正确的是( )
A.对角线互相垂直的四边形是菱形
B.一组对边相等,另一组对边平行的四边形是平行四边形
C.对角线相等的四边形是矩形
D.对角线互相垂直平分且相等的四边形是正方形
4.两个相似三角形的对应边上的中线比为1:,则它们面积比的为( )
A.2:1B.1:2C.1:D.:1
5.已知点A(﹣3,y1),B(0,y2),C(3,y3)都在二次函数y=﹣(x+2)2+4的图象上,则y1,y2,y3的大小关系是( )
A.y3<y2<y1B.y1=y3<y2C.y1<y2<y3D.y1<y3<y2
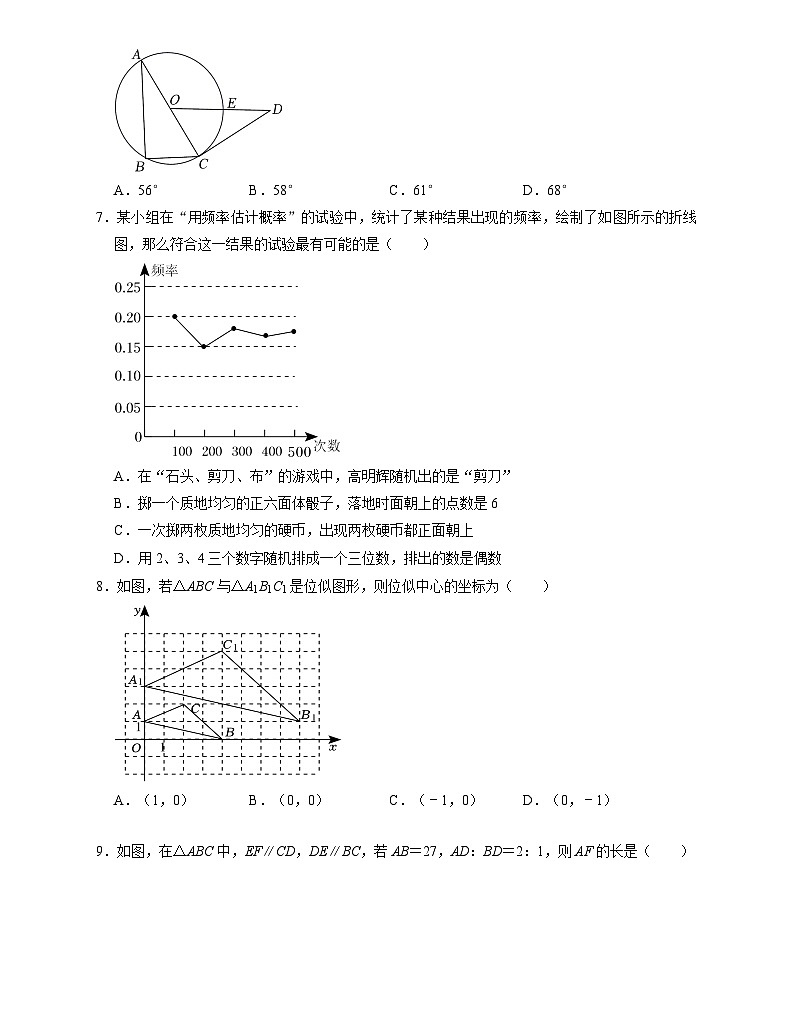
6.如图,AC是⊙O的直径,AB,BC是⊙O的弦,CD是⊙O的切线,C为切点,OD与⊙O交于点E.若点C为的中点,∠D=32°,则∠ACB的度数为( )
A.56°B.58°C.61°D.68°
7.某小组在“用频率估计概率”的试验中,统计了某种结果出现的频率,绘制了如图所示的折线图,那么符合这一结果的试验最有可能的是( )
A.在“石头、剪刀、布”的游戏中,高明辉随机出的是“剪刀”
B.掷一个质地均匀的正六面体骰子,落地时面朝上的点数是6
C.一次掷两枚质地均匀的硬币,出现两枚硬币都正面朝上
D.用2、3、4三个数字随机排成一个三位数,排出的数是偶数
8.如图,若△ABC与△A1B1C1是位似图形,则位似中心的坐标为( )
A.(1,0)B.(0,0)C.(﹣1,0)D.(0,﹣1)
9.如图,在△ABC中,EF∥CD,DE∥BC,若AB=27,AD:BD=2:1,则AF的长是( )
A.6B.9C.12D.18
10.如图,在正方形ABCD中,点E在BC上,点F在CD的延长线上.满足BE=DF,连接AE、AF,取AE的中点G,连接BG,FG,若BG=4,则FG=( )
A.B.C.D.
填空题(每小题3分,共15分)
11.点A(﹣2,m)和点B(n,6)关于原点对称,则m+n= .
12.已知关于x的一元二次方程x2+(m+3)x+m+1=0的两个实数根为x1,x2,若x12+x22=4,则m的值为 .
13.如图,将等边△OAB放在平面直角坐标系中,A点坐标(1,0),将△OAB绕点A顺时针旋转60°,则旋转后点B的对应点B′的坐标为 .
14.如图,圆O的直径AB垂直于弦CD,垂足是E,∠A=22.5°,OC=4,CD的长为 .
15.已知关于x的二次函数y=﹣(x﹣k)2+11,当1≤x≤4时,函数有最小值2k,则k的值为 .
三、解答题(本题共8小题,共75分.解答应写出文字说明、演算步骤或推理过程)
16.(10分)解方程:
(1)x2﹣4x﹣1=0;
(2)(x+3)2=x+3.
17.(8分).如图,方格纸中的每个小方格都是边长为1个单位的正方形,△ABC的顶点均在格点上.以点O为原点建立平面直角坐标系.
(1)将△ABC沿y轴向下平移4个单位得到△A1B1C1,画出△A1B1C1;
(2)将△ABC绕原点O逆时针旋转90°得到△A2B2C2,画出△A2B2C2;
(3)△A2B2C2可由△A1B1C1绕着点P旋转得到,点P的坐标是 ;线段B1C1扫过的面积是 .
18.(8分)已知关于x的一元二次方程x2+(2m+1)x+m2﹣2=0.
(1)若该方程有两个实数根,求m的最小整数值;
(2)若方程的两个实数根为x1,x2,且(x1﹣x2)2+m2=21,求m的值.
19.(8分)某商场经销A玩具,购进时的单价是60元.按照要求,销售时单件利润率不得超过40%.根据市场调查,销售单价定为80元时,每天可以卖出200件,而销售单价每降低1元,每天就可多售出20件.求销售单价定为多少时,该商场每天销售A玩具可以获利2500元.
20.(8分)如图,在Rt△ABC中,∠BCA=90°,点O是AC边上一点,⊙O经过点A交AB于点D,交AC于点F,过点D作⊙O的切线,交BC于点E.
(1)求证:∠BED=2∠A;
(2)若∠A=30°,AO=DE=4,求AB的长.
21.(8分)有一座抛物线形拱桥,正常水位时,桥下水面宽度为20m,拱顶距水面4m.
(1)如图所示的直角坐标系中,求出该抛物线的关系式.
(2)在正常水位的基础上,当水位上升h(m)时,桥下水面的宽度为d(m),求出将d表示为h的函数关系式.
(3)设正常水位时,桥下的水深为2m,为保证过往船只的顺利通过,桥下水面的宽度不得小于18m,求水深超过多少米时就会影响过往船只在桥下顺利航行?
22.(12分)(1)【探究发现】如图①,在等边三角形ABC内部,有一点P,若∠APB=150°.求证:AP2+BP2=CP2.下面是本题的部分解答过程,请补充完整.
证明:如图②,将△APC绕A点逆时针旋转60°得到△AP1B,连接P1A、P1B、P1P,则△APP1为等边三角形.完成接下来的证明.
(2)【类比延伸】如图③,在等腰三角形ABC中,∠BAC=90°,内部有一点P,若∠APB=135°,试判断线段PA、PB、PC之间的数量关系,并证明.
23.(13分)如图,抛物线y=ax2+bx+3(a≠0)经过x轴上A(﹣1,0)、B两点,抛物线的对称轴是直线x=1.
(1)求抛物线的函数表达式;
(2)抛物线与直线y=﹣x﹣1交于A、E两点,与y轴交于点C.点P在x轴上且位于点B的左侧,若以P,B,C为顶点的三角形与△ABE相似,求点P的坐标;
(3)F是直线BC上一点,D为抛物线上一点,是否存在点F,使得A,E,D,F四点组成的四边形是矩形?若存在,请求出点F的坐标,若不存在,请说明理由.
九年级数学参考答案
一.选择题(每题3分,共30分)ABDBA CBDCA
二、填空题(每小题3分,共15分)
11. —4 12. ﹣1或﹣3. 13. 14. 15. 1或.
三、解答题(共8小题,共75分)
16 (10分)解:(1)x2﹣4x﹣1=0,
x2﹣4x=1,
x2﹣4x+4=5,
(x﹣2)2=5,
,
,;
(2)(x+3)2=x+3,
(x+3)2﹣(x+3)=0,
(x+3)(x+3﹣1)=0,
(x+3)(x+2)=0,
x+3=0或x+2=0,
x1=﹣3,x2=﹣2.
17(8分)解:(1)如图所示,△A1B1C1即为所求;
(2)如图所示,△A2B2C2即为所求;
(3)如图所示,点P即为所求,P(﹣2,﹣2);
线段B1C1扫过的面积==.
18(8分).解:(1)根据题意得Δ=(2m+1)2﹣4(m2﹣2)≥0,
解得m≥﹣,
所以m的最小整数值为﹣2;
(2)根据题意得x1+x2=﹣(2m+1),x1x2=m2﹣2,
∵(x1﹣x2)2+m2=21,
∴(x1+x2)2﹣4x1x2+m2=21,
∴(2m+1)2﹣4(m2﹣2)+m2=21,
整理得m2+4m﹣12=0,解得m1=2,m2=﹣6,
∵m≥﹣,
∴m的值为2.
19(8分)解:设销售单价定为x元,则每件的销售利润为(x﹣60)元,每天可以卖出200+20(80﹣x)=(1800﹣20x)件,
根据题意得:(x﹣60)(1800﹣20x)=2500,
整理得:x2﹣150x+5525=0,
解得:x1=65,x2=85,
∵销售时利润不超过40%,
∴x≤60×(1+40%)=84,
∴x=85不符合题意,舍去.
∴x=65.
答:单价定为65元时,该商场每天销售A玩具可以获利2500元.
20.(8分)(1)证明:连接OD,如图,
∵DE与⊙O相切,
∴ED⊥OD
∴∠EDO=90°,
∵∠BCA=90°
∴∠BCA+∠EDO=180°,
∵∠BCA+∠EDO+∠DEC+∠DOC=360°,
∴∠DEC+∠DOC=180°,
∵∠DEC+∠BED=180°,
∴∠BED=∠DOC,
∵∠DOC=2∠A,
∴∠BED=2∠A;
(2)解:连接DF,如图,
∵AF为⊙O的直径,
∴∠ADF=90°,
在Rt△ADF中,∵∠A=30°,
∴DF=AF=OA=4,
∴AD=DF=4,
∵∠B=90°﹣∠A=60°,∠BED=2∠A=60°,
∴△BDE为等边三角形,
∴BD=DE=4,
∴AB=AD+BD=4+4.
21.(8分)解:(1)设二次函数解析式为y=ax2,
代入点(10,﹣4)得﹣4=100a,
解得a=﹣,
因此二次函数解析式为y=﹣x2;
(2)把点(,﹣4+h)代入函数解析式y=﹣x2,
得h=4﹣d2;
(3)当桥下水面的宽度等于18m时,抛物线上第四象限点的横坐标为9,
把x=9代入函数解析式y=﹣x2中,
∴y=﹣×92=﹣(米),
∴4+2﹣=.
答:当水深超过米时,超过了正常水位,就会影响过往船只在桥下顺利航行.
22.(12分)(1)证明:如图②,将△APC绕A点逆时针旋转60°得到△AP1B,连接P1A、P1B、P1P,如图:
由旋转性质可得AP=AP1,∠PAP1=60°,PC=BP1,
∴△APP1为等边三角形,
∴∠APP1=60°,PA=PP1,
∵∠APB=150°,
∴∠BPP1=∠APB﹣∠APP1=150°﹣60°=90°,
∴+BP2=,
∴PA2+PB2=PC2;
(2)2PA2+PB2=PC2,证明如下:
如图③,将△APC绕A点逆时针旋转90°得到△AP1B,连接P1A、P1B、P1P,
由旋转性质可得:PA=P1A,PC=P1B,∠PAP1=90°,
∴△APP1为等腰三角形,
∴∠APP1=45°,PP1=PA,
∵∠APB=135°,
∴∠BPP1=∠APB﹣∠APP1=135°﹣45°=90°,
∴+PB2=,
∴(PA)2+PB2=PC2,
∴2PA2+PB2=PC2.
23.(13分)解:(1)∵抛物线的对称轴是直线x=1,且过点A(﹣1,0),
∴点B的坐标为B(3,0),
将A(﹣1,0)、B(3,0)代入y=ax2+bx+3得:
,解得:,
∴抛物线的函数表达式为y=﹣x2+2x+3;
(2)如图:
由,解得:,,
∴点E的坐标为(4,﹣5),
∴AE==5,
在y=﹣x2+2x+3中,令x=0得y=3,
∴点C的坐标为(0,3),
∵点B的坐标为(3,0),
∴∠CBO=45°,BC=3,
∵直线AE的函数表达式为y=﹣x﹣1,
∴∠BAE=45°=∠CBO,
设点P的坐标为(m,0),则PB=3﹣m,
∵以P,B,C为顶点的三角形与△ABE相似,
∴=或=,
∴=或=,
解得:m=或m=﹣,
∴点P的坐标为(,0)或(﹣,0);
(3)不存在这样的点F,使A,E,D,F四点组成的四边形是矩形,理由如下:
若A,E,D,F四点组成的四边形是矩形,存在两种情况,
①假设AE为矩形的一边,则D,F必在直线AE的同侧,过A,E作直线AE的垂线交直线BC于F1,F2,交抛物线于D1、D2,如图:
由(2)可得,直线AE∥BC,
∴当点F必在F1,F2处,而点D必须在D1,D2处,
由图可知,此时A,E,D,F四点组成的四边形不存在是矩形的可能;
②假设AE为矩形的一对角线,则D,F必在直线AE的两侧,取AE的中点Q,以Q为圆心,以AQ为半径画⊙Q交直线BC于F1,F2,作射线F1Q交抛物线于D1,作射线F2Q交抛物线于D2,如图:
∴当点F必在F1,F2处,而点D必须在D1,D2处,
由图可知,此时A,E,D,F四点组成的四边形不存在是矩形的可能;
综上所述:不存在这样的点F,使A,E,D,F四点组成的四边形是矩形.
相关试卷
这是一份辽宁省辽阳市灯塔市2024-2025学年八年级上学期10月月考数学试题,共9页。试卷主要包含了答题前,考生须用0等内容,欢迎下载使用。
这是一份辽宁省辽阳市灯塔市2024-2025学年九年级上学期10月月考数学试题,共7页。试卷主要包含了答题前,考生须用0等内容,欢迎下载使用。
这是一份辽宁省辽阳市灯塔市2024-2025学年七年级上学期10月月考数学试题,共6页。试卷主要包含了答题前,考生须用0,87×103C.7,∵|x|=6,,等内容,欢迎下载使用。









