
所属成套资源:备战2025年高考数学一轮专题复习全套考点突破和专题检测(原卷版+解析)
- 备战2025年高考数学一轮专题复习全套考点突破和专题检测专题29求数列的通项公式10题型分类(原卷版+解析) 试卷 0 次下载
- 备战2025年高考数学一轮专题复习全套考点突破和专题检测专题30数列求和5题型分类(原卷版+解析) 试卷 0 次下载
- 备战2025年高考数学一轮专题复习全套考点突破和专题检测专题32空间点、直线、平面之间的位置关系5题型分类(原卷版+解析) 试卷 0 次下载
- 备战2025年高考数学一轮专题复习全套考点突破和专题检测专题33直线、平面平行的判定与性质6题型分类(原卷版+解析) 试卷 0 次下载
- 备战2025年高考数学一轮专题复习全套考点突破和专题检测专题34直线、平面垂直的判定与性质6题型分类(原卷版+解析) 试卷 0 次下载
备战2025年高考数学一轮专题复习全套考点突破和专题检测专题31空间几何体的结构特征、表面积与体积6题型分类练习
展开
这是一份备战2025年高考数学一轮专题复习全套考点突破和专题检测专题31空间几何体的结构特征、表面积与体积6题型分类练习,共94页。试卷主要包含了空间几何体的结构特征,柱、锥、台、球的表面积和体积,直观图与原平面图形面积间的关系等内容,欢迎下载使用。
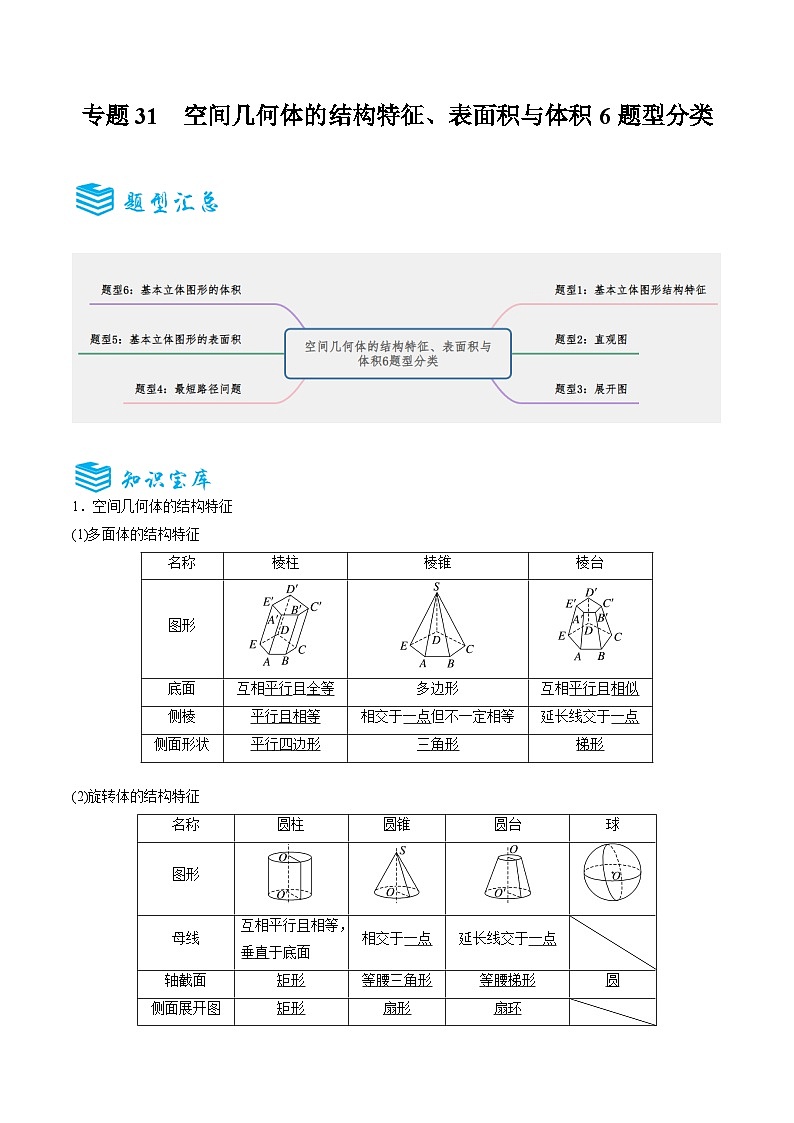
1.空间几何体的结构特征
(1)多面体的结构特征
(2)旋转体的结构特征
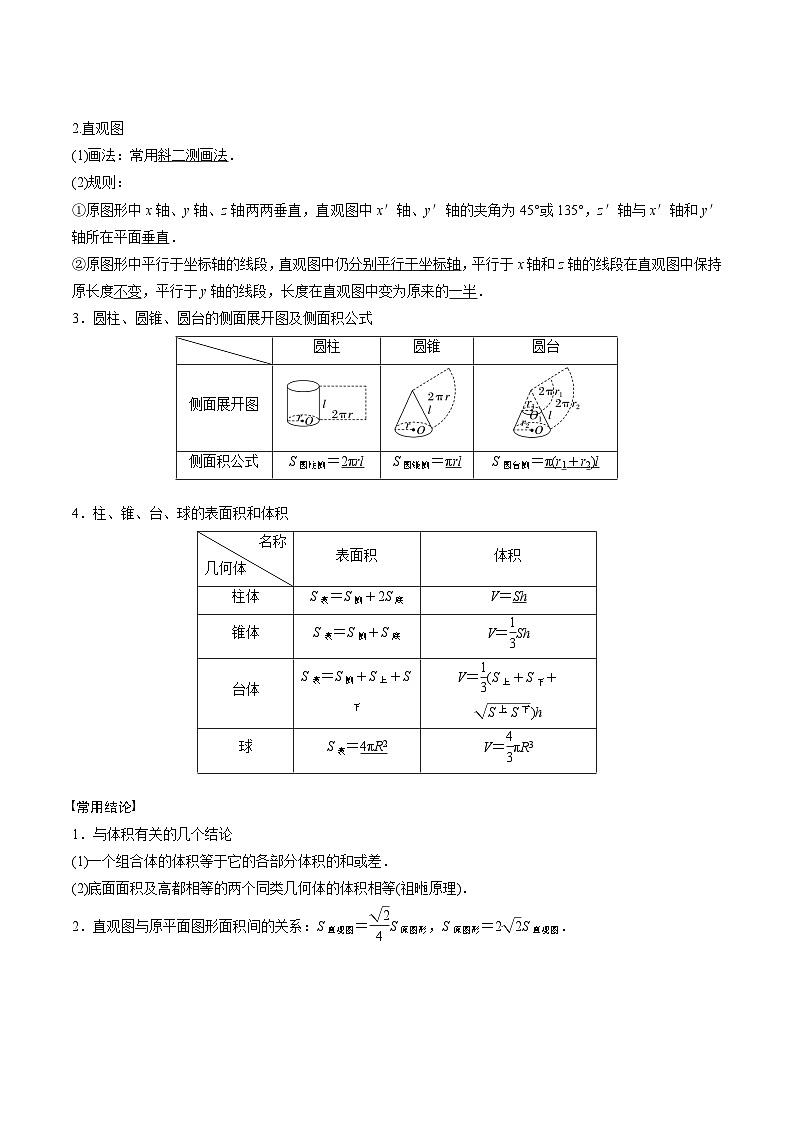
2.直观图
(1)画法:常用斜二测画法.
(2)规则:
①原图形中x轴、y轴、z轴两两垂直,直观图中x′轴、y′轴的夹角为45°或135°,z′轴与x′轴和y′轴所在平面垂直.
②原图形中平行于坐标轴的线段,直观图中仍分别平行于坐标轴,平行于x轴和z轴的线段在直观图中保持原长度不变,平行于y轴的线段,长度在直观图中变为原来的一半.
3.圆柱、圆锥、圆台的侧面展开图及侧面积公式
4.柱、锥、台、球的表面积和体积
常用结论
1.与体积有关的几个结论
(1)一个组合体的体积等于它的各部分体积的和或差.
(2)底面面积及高都相等的两个同类几何体的体积相等(祖暅原理).
2.直观图与原平面图形面积间的关系:S直观图=eq \f(\r(2),4)S原图形,S原图形=2eq \r(2)S直观图.
一、单选题
1.(2024高三下·安徽·阶段练习)已知几何体,“有两个面平行,其余各面都是平行四边形”是“几何体为棱柱”的( )
A.充分不必要条件B.必要不充分条件
C.充要条件D.既不充分也不必要条件
2.(2024高三·全国·对口高考)设有三个命题;甲:底面是平行四边形的四棱柱是平行六面体;乙:底面是矩形的平行六面体是长方体;丙:直四棱柱是平行六面体.以上命题中真命题的个数为( )
A.0个B.1个C.2个D.3个
3.(2024高二上·安徽合肥·阶段练习)如图所示,观察四个几何体,其中判断正确的是( )
A. 是棱台B. 是圆台
C. 不是棱柱D. 是棱锥
4.(2024·西藏拉萨·一模)位于徐州园博园中心位置的国际馆(一云落雨),使用现代科技雾化“造云”,打造温室客厅,如图,这个国际馆中3个展馆的顶部均采用正四棱锥这种经典几何形式,表达了理性主义与浪漫主义的对立与统一.其中最大的是3号展馆,其顶部所对应的正四棱锥底面边长为19.2m,高为9m,则该正四棱锥的侧面面积与底面面积之比约为( )(参考数据:)
A.2B.1.71C.1.37D.1
5.(2024高三下·湖南长沙·阶段练习)为了给热爱朗读的师生提供一个安静独立的环境,某学校修建了若干“朗读亭”.如图所示,该朗读亭的外形是一个正六棱柱和正六棱锥的组合体,正六棱柱两条相对侧棱所在的轴截面为正方形,若正六棱锥的高与底面边长的比为,则正六棱锥与正六棱柱的侧面积的比值为( )
A.B.C.D.
6.(2024·甘肃张掖·模拟预测)仿钧玫瑰紫釉盘是收藏于北京故宫博物院的一件明代宣德年间产的瓷器.该盘盘口微撇,弧腹,圈足.足底切削整齐.通体施玫瑰紫釉,釉面棕眼密集,美不胜收.仿钧玫瑰紫釉盘的形状可近似看成是圆台和圆柱的组合体,其口径为15.5cm,足径为9.2cm,顶部到底部的高为4.1cm,底部圆柱高为0.7cm,则该仿钧玫瑰紫釉盘圆台部分的侧面积约为( )(参考数据:π的值取3,)
A.B.C.D.
7.(2024·广东梅州·三模)在马致远的《汉宫秋》楔子中写道:“毡帐秋风迷宿草,穹庐夜月听悲笳.”毡帐是古代北方游牧民族以为居室、毡制帷幔.如图所示,某毡帐可视作一个圆锥与圆柱的组合体,圆锥的高为4,侧面积为,圆柱的侧面积为,则该毡帐的体积为( )
A.B.C.D.
8.(2024高三上·广东河源·开学考试)最早的测雨器记载见于南宋数学家秦九韶所著的《数书九章》(1247年).该书第二章为“天时类”,收录了有关降水量计算的四个例子,分别是“天池测雨”、“圆罂测雨”、“峻积验雪”和“竹器验雪”.如图“竹器验雪”法是下雪时用一个圆台形的器皿收集雪量(平地降雪厚度器皿中积雪体积除以器皿口面积),已知数据如图(注意:单位),则平地降雪厚度的近似值为( )
A.B.C.D.
9.(2024高一下·陕西宝鸡·期末)盲盒是一种深受大众喜爱的玩具,某盲盒生产厂商要为棱长为的正四面体魔方设计一款正方体的包装盒,需要保证该魔方可以在包装盒内任意转动,则包装盒的棱长最短为( )
A.B.C.D.
10.(2024高二下·安徽·阶段练习)我们知道立体图形上的最短路径问题通常是把立体图形展开成平面图形,连接两点,根据两点之间线段最短确定最短路线.请根据此方法求函数的最小值( )
A.B.C.D.
11.(2024·全国)已知圆锥PO的底面半径为,O为底面圆心,PA,PB为圆锥的母线,,若的面积等于,则该圆锥的体积为( )
A.B.C.D.
12.(2024·全国)南水北调工程缓解了北方一些地区水资源短缺问题,其中一部分水蓄入某水库.已知该水库水位为海拔时,相应水面的面积为;水位为海拔时,相应水面的面积为,将该水库在这两个水位间的形状看作一个棱台,则该水库水位从海拔上升到时,增加的水量约为()( )
A.B.C.D.
13.(2024高一·全国·课后作业)若一个正方体的体对角线长为a,则这个正方体的全面积为( )
A.B.C.D.
14.(2004·重庆)如图,棱长为5的正方体无论从哪一个面看,都有两个直通的边长为1的正方形孔,则这个有孔正方体的表面积(含孔内各面)是( )
A.258B.234C.222D.210
15.(2024高一下·贵州黔西·期末)端午节吃粽子是中华民族的传统习俗.地区不同,制作的粽子形状也不同,黔西南州最出名的就是鲜肉的灰色粽子,其形状接近于正三棱锥(如图).若正三棱锥的底面边长为2,高为1,则该三棱锥的侧面积为( )
A.B.C.D.
16.(2024·河南·模拟预测)在正四棱锥中,,若正四棱锥的体积是8,则该四棱锥的侧面积是( )
A.B.C.4D.
17.(2024高三上·辽宁·期末)已知四棱台的上、下底面分别是边长为和的正方形,侧面均为腰长为的等腰梯形,则该四棱台的表面积为( )
A.B.
C.D.
18.(2024高三上·广东·阶段练习)“李白斗酒诗百篇,长安市上酒家眠”,本诗句中的“斗”的本义是指盛酒的器具,后又作为计量粮食的工具,某数学兴趣小组利用相关材料制作了一个如图所示的正四棱台来模拟“斗”,用它研究“斗”的相关几何性质,已知该四棱台的上、下底的边长分别是2、4,高为1,则该四棱台的表面积为( )
A.B.32C.D.
19.(2024高三上·湖北·开学考试)已知正四棱台上底面边长为2,下底面边长4,高为3,则其表面积为( )
A.36B.
C.D.48
20.(2024高一下·全国·课后作业)已知一个圆柱的侧面展开图是一个正方形,则这个圆柱的全面积与侧面积的比是( )
A.B.C.D.
21.(2024·广东湛江·二模)如图,将一个圆柱等分切割,再将其重新组合成一个与圆柱等底等高的几何体,越大,重新组合成的几何体就越接近一个“长方体”.若新几何体的表面积比原圆柱的表面积增加了10,则圆柱的侧面积为( )
A.B.C.D.
22.(2024·福建)以边长为的正方形的一边所在直线为旋转轴,将该正方形旋转一周所得圆柱的侧面积等于
A.B.C.D.
23.(2024高三上·全国·阶段练习)已知圆锥的底面半径为2,高为,则该圆锥的侧面积为( )
A.B.C.D.
24.(2024·四川成都·二模)若圆锥的表面积为,底面圆的半径为,则该圆锥的高为( )
A.B.C.D.
25.(2024高三上·河南·阶段练习)佛兰德现代艺术中心是比利时洛默尔市的地标性建筑,该建筑是一座全玻璃建筑,整体成圆锥形,它利用现代设计手法令空间与其展示的艺术品无缝交融,形成一个统一的整体,气势恢宏,美轮美英.佛兰德现代艺术中心的底面直径为,侧面积为,则该建筑的高为( )
A.B.C.D.
26.(2024高三上·河南·开学考试)圆台轴截面面积为,上下底面半径之比为,母线与底面所成角为,则圆台侧面积为( )
A.B.
C.D.
27.(2024高二上·江苏镇江·开学考试)已知圆台的上下底面半径分别为2和5,且母线与下底面所成为角的正切值为,则该圆台的表面积为( )
A.B.C.D.
28.(2024·甘肃兰州·模拟预测)攒尖是中国古建筑中屋顶的一种结构形式,常见的有圆形攒尖、三角攒尖、四角攒尖、六角攒尖等,多见于亭阁式建筑,兰州市著名景点三台阁的屋顶部分也是典型的攒尖结构.如图所示是某研究性学习小组制作的三台阁仿真模型的屋顶部分,它可以看作是不含下底面的正四棱台和正三棱柱的组合体,已知正四棱台上底、下底、侧棱的长度(单位:dm)分别为2,6,4,正三棱柱各棱长均相等,则该结构表面积为( )
A.B.C.D.
29.(2024高三上·黑龙江哈尔滨·期中)正三棱柱侧面的一条对角线长为2,且与底面成角,则此三棱柱的体积为( )
A.B.C.D.
30.(2008·四川)若三棱柱的一个侧面是边长为2的正方形,另外两个侧面都是有一个内角为的菱形,则该棱柱的体积等于
A.B.C.D.
31.(2024高三上·河南焦作·开学考试)把过棱锥的顶点且与底面垂直的直线称为棱锥的轴,过棱锥的轴的截面称为棱锥的轴截面.现有一个正三棱锥、一个正四棱锥、一个正六棱锥,它们的高相等,轴截面面积的最大值也相等,则此正三棱锥、正四棱锥、正六棱锥的体积之比为( )
A.B.
C.D.
32.(2024·广东深圳·二模)设表面积相等的正方体、正四面体和球的体积分别为、和,则( )
A.B.C.D.
33.(2024·河南郑州·模拟预测)《九章算术·商功》:“斜解立方,得两堑堵,斜解堑堵,其一为阳马,其一为鳖臑”.意思是一个长方体沿对角面斜解(图1),得到一模一样的两个堑堵(图2),再沿一个堑堵的一个顶点和相对的棱斜解(图2),得一个四棱锥称为阳马(图3),一个三棱锥称为鳖臑(图4).若长方体的体积为,由该长方体斜解所得到的堑堵、阳马和鳖臑的体积分别为,,,则下列等式错误的是( )
A.B.
C.D.
34.(2024高三下·浙江杭州·阶段练习)已知矩形中,,,是的中点,沿直线将△翻折成△,则三棱锥的体积的最大值为( )
A.B.C.D.
35.(2024·全国)正四棱台的上、下底面的边长分别为2,4,侧棱长为2,则其体积为( )
A.B.C.D.
36.(2024高一下·江苏连云港·阶段练习)在《九章算术商功》中将正四面形棱台体棱台的上、下底面均为正方形称为方亭.在方亭中,,四个侧面均为全等的等腰梯形且面积之和为,则该方亭的体积为( )
A.B.C.D.
37.(2024高三上·山西运城·期中)已知一个正四棱台的上下底面边长为、,侧棱长为,则棱台的体积为( )
A.B.C.D.
38.(2024·河南·模拟预测)光岳楼,又称“余木楼”“鼓楼”“东昌楼”,位于山东省聊城市,在《中国名楼》站台票纪念册中,光岳楼与鹳雀楼、黄鹤楼、岳阳楼、太白楼、滕王阁、蓬莱阁、镇海楼、甲秀楼、大观楼共同组成中国十大名楼.其墩台为砖石砌成的正四棱台,如图所示,光岳楼的墩台上底面正方形的边长约为32m,下底面正方形的边长约为34.5m,高的4倍比上底面的边长长4m,则光岳楼墩台的体积约为( )
A.B.C.D.
39.(四川省仁寿第一中学校(北校区)2023-2024学年高三上学期9月月考文科数学试题)已知圆柱的高为1,它的两个底面的圆周在直径为2的同一个球的球面上,则该圆柱的体积为( )
A.B.C.D.
40.(2024高三上·江苏苏州·开学考试)若某圆柱体的底面半径与某球体的半径相等,圆柱体与球体的体积之比和它们的表面积之比的比值相等,则该圆柱体的高与球体的半径的比值为( )
A.B.C.D.2
41.(2024·河南·模拟预测)圆锥的高为2,其侧面展开图的圆心角为,则该圆锥的体积为( ).
A.B.C.D.
42.(2024高三上·福建厦门·阶段练习)已知母线长为5的圆锥的侧面积为,则这个圆锥的体积为( )
A.B.C.D.
43.(2024高三下·河南开封·阶段练习)木桶作为一种容器,在我国使用的历史已经达到了几千年,其形状可视为一个圆台.若某圆台形木桶上、下底面的半径分别为,母线长为,木板厚度忽略不计,则该木桶的容积为( )
A.B.C.D.
44.(2024高三上·福建厦门·阶段练习)用一个平行于圆锥底面的平面截该圆锥得到一个圆台,若圆台上底面和下底面半径之比为,则该圆台与圆锥的体积之比为( )
A.B.C.D.
二、多选题
45.(2024·全国)如图,四边形为正方形,平面,,记三棱锥,,的体积分别为,则( )
A.B.
C.D.
46.(2024·福建·模拟预测)等腰梯形的上下底边之比为,若绕该梯形的对称轴旋转一周所得几何体的表面积为,则该梯形的周长可能为( )
A.B.8C.D.16
47.(2024·河南·模拟预测)如图,正三棱柱的底面边长为1,高为3,为棱的中点,分别在棱上,且满足取得最小值.记四棱锥、三棱锥的体积分别为,则( )
A.B.C.D.
48.(2024高三上·湖南·阶段练习)若某正方体的棱长为,则( )
A.该正方体的体积为5B.该正方体的内切球的体积为
C.该正方体的表面积为30D.该正方体的外接球的表面积为
三、填空题
49.(2024·辽宁锦州·模拟预测)已知用斜二测画法画梯形OABC的直观图如图所示,,,,轴,,为的三等分点,则四边形OABC绕y轴旋转一周形成的空间几何体的体积为 .
50.(2024高三·全国·对口高考)若正用斜二测画法画出的水平放置图形的直观图为,当的面积为时,的面积为 .
51.(2024高三下·上海宝山·开学考试)我们知道一条线段在“斜二测”画法中它的长度可能会发生变化的,现直角坐标系平面上一条长为4cm线段AB按“斜二测”画法在水平放置的平面上画出为,则最短长度为 cm(结果用精确值表示)
52.(2024高三·全国·阶段练习)如图,梯形ABCD是水平放置的一个平面图形的直观图,其中,,,则原图形的面积为 .
53.(2024高三上·上海普陀·期中)2022年4月16日,神舟十三号载人飞船返回舱在东风着陆场预定区域成果着陆.如图,在返回过程中使用的主降落伞外表面积达到1200平方米,若主降落伞完全展开后可以近似看着一个半球,则完全展开后伞口的直径约为 米(精确到整数)
54.(2024高一下·四川成都·阶段练习)已知圆锥的底面半径为1,其侧面展开图为一个半圆,则该圆锥的体积为 .
55.(2024·安徽·模拟预测)如图,在三棱锥P-ABC的平面展开图中,,,,,,则三棱锥外接球表面积为 .
56.(2024·安徽马鞍山·模拟预测)已知三棱锥P-ABC的底面ABC为等边三角形.如图,在三棱锥P-ABC的平面展开图中,P,F,E三点共线,B,C,E三点共线,,,则PB= .
57.(2024高三上·山西大同·阶段练习)如图,在三棱锥的平面展开图中,,,,,,则三棱锥的外接球的表面积为 .
58.(2024高三·河北·专题练习)如图,正方体的棱长为,点为的中点,在对角面上取一点,使最小,其最小值为
59.(2024高三上·四川成都·开学考试)如图一个正六棱柱的茶叶盒,底面边长为,高为,则这个茶叶盒的表面积为 .
60.(2024高二上·上海黄浦·阶段练习)若长方体的对角线的长为,其长、宽、高的和是,则长方体的全面积是 .
61.(2024·全国·模拟预测)正四棱锥P-ABCD的各条棱长均为2,则该四棱锥的表面积为 .
62.(2024高三·全国·专题练习)一个正三棱台的上、下底面边长分别是3 cm和6 cm,高是cm.则三棱台的斜高为 ;三棱台的侧面积为 ;表面积为 .
63.(2024高三·全国·专题练习)若矩形的周长为36,矩形绕它的一条边旋转形成一个圆柱,求圆柱侧面积的最大值为 .
64.(2024高二上·北京海淀·期中)若一个圆锥的轴截面是等边三角形,其面积为,则这个圆锥的侧面积是 .
65.(2024高三上·全国·专题练习)某地球仪上北纬纬线的长度为,该地球仪的半径是 cm,
表面积是 cm2.
66.(2024·全国)已知圆和圆是球的大圆和小圆,其公共弦长等于球的半径,,且圆与圆所在的平面所成的一个二面角为则球的表面积等于 .
67.(2009年普通高等学校招生全国统一考试理科数学(全国卷Ⅱ))设OA是球O的半径,M是OA的中点,过M且与OA成角的平面截球O的表面得到圆C.若圆C的面积等于,则球O的表面积等于
68.(2024·全国)用平面截半径为的球,如果球心到截面的距离为,那么截得小圆的面积与球的表面积的比值为 .
69.(2024高三上·广东广州·阶段练习)陀螺是中国民间较早的娱乐工具之一,也称陀罗,图l是一种木陀螺,可近似地看作是一个圆锥和一个圆柱的组合体,其直观图如图2所示,其中A是圆锥的顶点,B,C分别是圆柱的上、下底面圆的圆心,且,,底面圆的半径为1,则该陀螺的表面积是 .
70.(2024高三·全国·专题练习)如图,八面体的每一个面都是正三角形,并且4个顶点A,B,C,D在同一个平面内.如果四边形ABCD是边长为30 cm的正方形,那么这个八面体的表面积是 .
71.(2024高三上·天津北辰·阶段练习)已知一个圆柱的高是底面半径的2倍,且其上、下底面的圆周均在球面上,若球的体积为,则圆柱的体积为 .
72.(2024高三上·云南昆明·阶段练习)已知某圆锥的侧面展开图是一个半径为的半圆、则该圆锥的体积为 .
73.(2024·浙江嘉兴·模拟预测)已知圆锥的底面半径为1,侧面积为,则此圆锥的体积是 .
74.(2024高三上·广东广州·阶段练习)已知圆锥的底面半径为2,侧面展开图是一个圆心角为120°的扇形.把该圆锥截成圆台,已知圆台的下底面与该圆锥的底面重合,圆台的上底面半径为1,则圆台的体积为
成套的课件成套的教案成套的试题成套的微专题尽在高中数学同步资源大全QQ群552511468也可联系微信fjshuxue加入百度网盘群1.5T一线老师必备资料一键转存自动更新永不过期
名称
棱柱
棱锥
棱台
图形
底面
互相平行且全等
多边形
互相平行且相似
侧棱
平行且相等
相交于一点但不一定相等
延长线交于一点
侧面形状
平行四边形
三角形
梯形
名称
圆柱
圆锥
圆台
球
图形
母线
互相平行且相等,垂直于底面
相交于一点
延长线交于一点
轴截面
矩形
等腰三角形
等腰梯形
圆
侧面展开图
矩形
扇形
扇环
圆柱
圆锥
圆台
侧面展开图
侧面积公式
S圆柱侧=2πrl
S圆锥侧=πrl
S圆台侧=π(r1+r2)l
名称
几何体
表面积
体积
柱体
S表=S侧+2S底
V=Sh
锥体
S表=S侧+S底
V=eq \f(1,3)Sh
台体
S表=S侧+S上+S下
V=eq \f(1,3)(S上+S下+eq \r(S上S下))h
球
S表=4πR2
V=eq \f(4,3)πR3
(一)
1.空间几何体结构特征的判断技巧
(1)说明一个命题是错误的,只要举出一个反例即可.
(2)在斜二测画法中,平行于x轴的线段平行性不变,长度不变;平行于y轴的线段平行性不变,长度减半.
(3)在解决空间折线(段)最短问题时一般考虑其展开图,采用化曲为直的策略,将空间问题平面化.
2.多面体表面展开图可以有不同的形状,应多实践,观察并大胆想象立体图形与表面展开图的关系,一定先观察立体图形的每一个面的形状.
3.最大路径问题:大胆展开,把问题变为平面两点间线段最短问题.
题型1:基本立体图形结构特征
1-1.(2024·新疆·模拟预测)下列命题中正确的是( )
A.有两个平面平行,其余各面都是平行四边形的几何体是棱柱.
B.各个面都是三角形的几何体是三棱锥.
C.夹在圆柱的两个平行截面间的几何体还是一个旋转体.
D.圆锥的顶点与底面圆周上任意一点的连线都是母线.
1-2.(2024高一·全国·课后作业)下列命题:
①有两个面平行,其他各面都是平行四边形的几何体叫做棱柱;
②有两侧面与底面垂直的棱柱是直棱柱;
③过斜棱柱的侧棱作棱柱的截面,所得图形不可能是矩形;
④所有侧面都是全等的矩形的四棱柱一定是正四棱柱.
其中正确命题的个数为( )
A.0B.1C.2D.3
1-3.(2024高一下·山西吕梁·期末)下列说法正确的是( )
A.三角形的直观图是三角形B.直四棱柱是长方体
C.平行六面体不是棱柱 D.两个平面平行,其余各面是梯形的多面体是棱台
1-4.(2024高三·全国·专题练习)给出下列命题:
①在圆柱的上、下底面的圆周上各取一点,则这两点的连线是圆柱的母线;
②直角三角形绕其任一边所在直线旋转一周所形成的几何体都是圆锥;
③棱台的上、下底面可以不相似,但侧棱长一定相等.
其中正确命题的个数是( )
A.B.C.D.
题型2:直观图
2-1.(2024高一下·浙江宁波·期中)用斜二测画法画出的某平面图形的直观图如图所示,边与平行于轴.已知四边形的面积为,则原平面图形的面积为 .
2-2.(2024高一下·上海奉贤·期末)如图,是用斜二测画法得到的△AOB的直观图,其中则AB的长度为 .
2-3.(2024高一上·山东济宁·阶段练习)有一块多边形的菜地,它的水平放置的平面图形的斜二测直观图是直角梯形(如图所示).,则这块菜地的面积为
2-4.(2024高二上·宁夏石嘴山·阶段练习)如图,用斜二测画法画一个水平放置的平面图形的直观图为一个正方形,则原来图形的面积是 .
题型3:展开图
3-1.(2024·山东青岛·三模)已知圆锥的底面半径为1,侧面展开图为半圆,则该圆锥内半径最大的球的表面积为 .
3-2.(2024高二下·云南红河·阶段练习)如图,在直三棱柱的侧面展开图中,B,C是线段AD的三等分点,且.若该三棱柱的外接球O的表面积为12π,则 .
3-3.(2024·安徽黄山·一模)如图,在四棱锥P-ABCD的平面展开图中,正方形ABCD的边长为4,是以AD为斜边的等腰直角三角形,,则该四棱锥外接球被平面PBC所截的圆面的面积为 .
题型4:最短路径问题
4-1.(2024高三·全国·专题练习)如图,一竖立在地面上的圆锥形物体的母线长为4,一只小虫从圆锥的底面圆上的点P出发,绕圆锥爬行一周后回到点P处,若该小虫爬行的最短路程为,则这个圆锥的体积为( ).
A.B.C.D.
4-2.(2024高一下·河南开封·期中)如图,已知正四棱锥的侧棱长为,侧面等腰三角形的顶角为,则从A点出发环绕侧面一周后回到A点的最短路程为( )
A.B.C.D.6
4-3.(2024·辽宁·三模)盲盒是一种深受大众喜爱的玩具,某盲盒生产厂商要为棱长为的正四面体魔方设计一款正方体的包装盒,需要保证该魔方可以在包装盒内任意转动,则包装盒的棱长最短为( )
A.B.C.D.
4-4.(2024高一下·湖北武汉·期中)如图,一个矩形边长为1和4,绕它的长为的边旋转二周后所得如图的一开口容器(下表面密封),是中点,现有一只妈蚁位于外壁处,内壁处有一米粒,若这只蚂蚁要先爬到上口边沿再爬到点处取得米粒,则它所需经过的最短路程为( )
A.B.C.D.
4-5.(2024高一·全国·课后作业)如图所示,在正三棱柱中,,,由顶点沿棱柱侧面(经过棱)到达顶点,与的交点记为,则从点经点到的最短路线长为( )
A.B.C.4D.
(二)
基本立体图形的表面积的体积
1.(1)多面体的表面积是各个面的面积之和.
(2)旋转体的表面积是将其展开后,展开图的面积与底面面积之和.
(3)组合体的表面积求解时注意对衔接部分的处理.
2.空间几何体的体积的常用方法
公式法
规则几何体的体积,直接利用公式
割补法
把不规则的几何体分割成规则的几何体,或者把不规则的几何体补成规则的几何体
等体积法
通过选择合适的底面来求几何体体积的一种方法,特别是三棱锥的体积
题型5:基本立体图形的表面积
5-1.(2024·湖北武汉·模拟预测)已知某圆锥的母线长、底面圆的直径都等于球的半径,则球与圆锥的表面积之比为( )
A.8B.C.D.
5-2.(2024·河南郑州·模拟预测)在一个正六棱柱中挖去一个圆柱后,剩余部分几何体如图所示.已知正六棱柱的底面正六边形边长为3cm,高为4cm,内孔半径为1cm,则此几何体的表面积是( ).
A.B.
C.D.
5-3.(2024·安徽安庆·三模)陀螺起源于我国,最早出土的石制陀螺是在山西夏县发现的新石器时代遗址.如图所示的是一个陀螺立体结构图.已知,底面圆的直径,圆柱体部分的高,圆锥体部分的高,则这个陀螺的表面积(单位:)是( )
A.B.
C.D.
5-4.(2024·河北·模拟预测)《九章算术》是我国古代的数学名著.其“商功”中记载:“正四面形棱台(即正四棱台)建筑物为方亭.”现有如图所示的烽火台,其主体部分为一方亭,将它的主体部分抽象成的正四棱台(如图所示),其中上底面与下底面的面积之比为,方亭的高为棱台上底面边长的倍.已知方亭的体积为,则该方亭的表面积约为( )(,,)
A.B.C.D.
5-5.(2024高三下·海南海口·期中)如图是一个圆台形的水杯,圆台的母线长为12,上、下底面的半径分别为4和2.为了防烫和防滑,该水杯配有一个皮革杯套,包裹住水杯高度以下的外壁和杯底,水杯和杯套的厚度忽略不计,则此杯套使用的皮革的面积为( )
A.B.C.D.
题型6:基本立体图形的体积
6-1.(2024高三上·重庆沙坪坝·阶段练习)若某圆锥的侧面展开图是一个半径为2的半圆面,其内接正四棱柱的高为,则此正四棱柱的体积是( )
A.B.C.D.
6-2.(2024高三上·山东青岛·期中)已知正四棱锥的各顶点都在同一个球面上,球的体积为,则该正四棱锥的体积最大值为( )
A.18B.C.D.27
6-3.(2024高三上·湖北武汉·开学考试)攒尖是我国古代建筑中屋顶的一种结构形式,宋代称为最尖,清代称攒尖,通常有圆形攒尖、三角攒尖、四角攒尖、八角攒尖,也有单檐和重檐之分,多见于亭阁式建筑、园林建筑.下面以四角攒尖为例,如图,它的屋顶部分的轮廓可近似看作一个正四棱锥.已知正四棱锥的底面边长为米,侧棱长为5米,则其体积为( )立方米.
A.B.24C.D.72
6-4.(2024·浙江·模拟预测)如图是我国古代量粮食的器具“升”,其形状是正四棱台,上、下底面边长分别为20cm和10cm,侧棱长为cm.“升”装满后用手指或筷子沿升口刮平,这叫“平升”.则该“升”的“平升”约可装( )
A.1.5LB.1.7LC.2.3LD.2.7L
6-5.(2024高三上·广西·阶段练习)在棱长为2的正方体内,放入一个以为铀线的圆柱,且圆柱的底面所在平面截正方体所得的截面为三角形,则该圆柱体积的最大值为 .
专题31 空间几何体的结构特征、表面积与体积6题型分类
1.空间几何体的结构特征
(1)多面体的结构特征
(2)旋转体的结构特征
2.直观图
(1)画法:常用斜二测画法.
(2)规则:
①原图形中x轴、y轴、z轴两两垂直,直观图中x′轴、y′轴的夹角为45°或135°,z′轴与x′轴和y′轴所在平面垂直.
②原图形中平行于坐标轴的线段,直观图中仍分别平行于坐标轴,平行于x轴和z轴的线段在直观图中保持原长度不变,平行于y轴的线段,长度在直观图中变为原来的一半.
3.圆柱、圆锥、圆台的侧面展开图及侧面积公式
4.柱、锥、台、球的表面积和体积
常用结论
1.与体积有关的几个结论
(1)一个组合体的体积等于它的各部分体积的和或差.
(2)底面面积及高都相等的两个同类几何体的体积相等(祖暅原理).
2.直观图与原平面图形面积间的关系:S直观图=eq \f(\r(2),4)S原图形,S原图形=2eq \r(2)S直观图.
一、单选题
1.(2024高三下·安徽·阶段练习)已知几何体,“有两个面平行,其余各面都是平行四边形”是“几何体为棱柱”的( )
A.充分不必要条件B.必要不充分条件
C.充要条件D.既不充分也不必要条件
【答案】B
【分析】利用充分条件和必要条件,结合棱柱的定义判断.
【详解】由棱柱定义知棱柱有两个面平行,其余各面都是平行四边形,故满足必要性;
但有两个面平行,其余各面都是平行四边形的几何体不一定是棱柱,
例如两个底面全等的斜棱柱拼接的几何体不是棱柱,如图所示:
,
故不满足充分性,
故选:B
2.(2024高三·全国·对口高考)设有三个命题;甲:底面是平行四边形的四棱柱是平行六面体;乙:底面是矩形的平行六面体是长方体;丙:直四棱柱是平行六面体.以上命题中真命题的个数为( )
A.0个B.1个C.2个D.3个
【答案】B
【分析】根据平行六面体,长方体,直棱柱的定义判断三个命题即可.
【详解】由平行六面体的定义可得底面是平行四边形的四棱柱是平行六面体;命题甲正确;
底面是矩形的平行六面体的侧棱不一定垂直于底面,故该几何体不一定为长方体,
命题乙错误;
直四棱柱的底面不一定为平行四边形,故直四棱柱不一定是平行六面体,命题丙错误;
正确的命题只有一个.
故选:B
3.(2024高二上·安徽合肥·阶段练习)如图所示,观察四个几何体,其中判断正确的是( )
A. 是棱台B. 是圆台
C. 不是棱柱D. 是棱锥
【答案】D
【分析】根据棱台,圆台,棱柱,棱锥的概念即可判断.
【详解】对A,侧棱延长线不交于一点,不符合棱台的定义,所以A错误;
对B,上下两个面不平行,不符合圆台的定义,所以B错误;
对C,将几何体竖直起来看,符合棱柱的定义,所以C错误;
对D,符合棱锥的定义,正确.
故选:D.
【点睛】本题主要考查棱台,圆台,棱柱,棱锥的概念的理解,属于基础题.
4.(2024·西藏拉萨·一模)位于徐州园博园中心位置的国际馆(一云落雨),使用现代科技雾化“造云”,打造温室客厅,如图,这个国际馆中3个展馆的顶部均采用正四棱锥这种经典几何形式,表达了理性主义与浪漫主义的对立与统一.其中最大的是3号展馆,其顶部所对应的正四棱锥底面边长为19.2m,高为9m,则该正四棱锥的侧面面积与底面面积之比约为( )(参考数据:)
A.2B.1.71C.1.37D.1
【答案】C
【分析】根据图形,作出直观图,利用正四棱锥的相关性质即可求解.
【详解】如图,设H为底面正方形ABCD的中心,G为BC的中点,连接PH,HG,PG,
则,,
所以,
则,
故选:C.
5.(2024高三下·湖南长沙·阶段练习)为了给热爱朗读的师生提供一个安静独立的环境,某学校修建了若干“朗读亭”.如图所示,该朗读亭的外形是一个正六棱柱和正六棱锥的组合体,正六棱柱两条相对侧棱所在的轴截面为正方形,若正六棱锥的高与底面边长的比为,则正六棱锥与正六棱柱的侧面积的比值为( )
A.B.C.D.
【答案】B
【分析】设出相关棱长,利用面积公式求出正六棱锥与正六棱柱的侧面积,然后可得答案.
【详解】设正六边形的边长为,由题意正六棱柱的高为,
因为正六棱锥的高与底面边长的比为,所以正六棱锥的高为,正六棱锥的母线长为,
正六棱锥的侧面积;
正六棱柱的侧面积,
所以.
故选:B.
6.(2024·甘肃张掖·模拟预测)仿钧玫瑰紫釉盘是收藏于北京故宫博物院的一件明代宣德年间产的瓷器.该盘盘口微撇,弧腹,圈足.足底切削整齐.通体施玫瑰紫釉,釉面棕眼密集,美不胜收.仿钧玫瑰紫釉盘的形状可近似看成是圆台和圆柱的组合体,其口径为15.5cm,足径为9.2cm,顶部到底部的高为4.1cm,底部圆柱高为0.7cm,则该仿钧玫瑰紫釉盘圆台部分的侧面积约为( )(参考数据:π的值取3,)
A.B.C.D.
【答案】D
【分析】方法1,根据圆台上下底面圆的半径和高,求母线长,再代入圆台侧面积公式,即可求解;方法2,采用估算的方法,先估算底面直径为15.5cm,高为3.4cm的圆柱的侧面积,再比较选项,即可判断.
【详解】方法1:设该圆台的母线长为l,高为h,两底面圆的半径分别为R,r(其中),
则,,,
所以,故圆台部分的侧面积为.
故选:D
方法2(估算法):若按底面直径为15.5cm,高为3.4cm的圆柱估算圆台部分的侧面积得,易知圆台的侧面积应大于所估算的圆柱的侧面积,故此仿钧玫瑰紫釉盘圆台部分的侧面积大于,对照各选项可知只有D符合.
故选:D
7.(2024·广东梅州·三模)在马致远的《汉宫秋》楔子中写道:“毡帐秋风迷宿草,穹庐夜月听悲笳.”毡帐是古代北方游牧民族以为居室、毡制帷幔.如图所示,某毡帐可视作一个圆锥与圆柱的组合体,圆锥的高为4,侧面积为,圆柱的侧面积为,则该毡帐的体积为( )
A.B.C.D.
【答案】A
【分析】直接利用圆锥侧面积公式以及母线、底面半径和高的关系得到方程组即可解出圆锥底面半径,再利用圆柱侧面积公式即可求圆柱的高,最后再根据相关体积公式即可得到答案.
【详解】设圆柱的底面半径为,高为,圆锥的母线长为,
因为圆锥的侧面积为,所以,即.
因为,所以联立解得(负舍).
因为圆柱的侧面积为,所以,即,解得,
所以该毡帐的体积为.
故选:A.
8.(2024高三上·广东河源·开学考试)最早的测雨器记载见于南宋数学家秦九韶所著的《数书九章》(1247年).该书第二章为“天时类”,收录了有关降水量计算的四个例子,分别是“天池测雨”、“圆罂测雨”、“峻积验雪”和“竹器验雪”.如图“竹器验雪”法是下雪时用一个圆台形的器皿收集雪量(平地降雪厚度器皿中积雪体积除以器皿口面积),已知数据如图(注意:单位),则平地降雪厚度的近似值为( )
A.B.C.D.
【答案】C
【分析】根据梯形中位线定理,结合圆台体积公式进行求解即可.
【详解】如图所示,可求得器皿中雪表面的半径为,
所以平地降雪厚度的近似值为.
故选:C
9.(2024高一下·陕西宝鸡·期末)盲盒是一种深受大众喜爱的玩具,某盲盒生产厂商要为棱长为的正四面体魔方设计一款正方体的包装盒,需要保证该魔方可以在包装盒内任意转动,则包装盒的棱长最短为( )
A.B.C.D.
【答案】A
【分析】根据题意,要使得正四面体能自由转动,则正方体必须能装下正四面体的外接球,即正方体的最短棱长为正四面体的外接球的直径,根据求得正四面体的外接球的半径,即可求解.
【详解】如图所示,根据题意可得,
设的中点为,底面的重心为,为外接球的球心,
则有底面,,,
且,其中为外接球的半径,
在直角中,可得,
在直角中,,且,
所以,解得,
所以正方体的最短棱长为.
故选:A.
10.(2024高二下·安徽·阶段练习)我们知道立体图形上的最短路径问题通常是把立体图形展开成平面图形,连接两点,根据两点之间线段最短确定最短路线.请根据此方法求函数的最小值( )
A.B.C.D.
【答案】A
【分析】
构造合适的三棱锥模型,其中,,利用余弦定理证明即为底面周长,最后将其展开即可得到最小值.
【详解】根据函数的表达式可知,构造三棱锥,其中,且,
由余弦定理可得,,,
的最小值即为的最小值,
将三棱锥按照展开可得展开图,且,
故的最小值为.
故选:A.
11.(2024·全国)已知圆锥PO的底面半径为,O为底面圆心,PA,PB为圆锥的母线,,若的面积等于,则该圆锥的体积为( )
A.B.C.D.
【答案】B
【分析】根据给定条件,利用三角形面积公式求出圆锥的母线长,进而求出圆锥的高,求出体积作答.
【详解】在中,,而,取中点,连接,有,如图,
,,由的面积为,得,
解得,于是,
所以圆锥的体积.
故选:B
12.(2024·全国)南水北调工程缓解了北方一些地区水资源短缺问题,其中一部分水蓄入某水库.已知该水库水位为海拔时,相应水面的面积为;水位为海拔时,相应水面的面积为,将该水库在这两个水位间的形状看作一个棱台,则该水库水位从海拔上升到时,增加的水量约为()( )
A.B.C.D.
【答案】C
【分析】根据题意只要求出棱台的高,即可利用棱台的体积公式求出.
【详解】依题意可知棱台的高为(m),所以增加的水量即为棱台的体积.
棱台上底面积,下底面积,
∴
.
故选:C.
13.(2024高一·全国·课后作业)若一个正方体的体对角线长为a,则这个正方体的全面积为( )
A.B.C.D.
【答案】A
【分析】设正方体的棱长为x,求出正方体的棱长即得解.
【详解】解:设正方体的棱长为x,则,即,
所以正方体的全面积为.
故选:A
14.(2004·重庆)如图,棱长为5的正方体无论从哪一个面看,都有两个直通的边长为1的正方形孔,则这个有孔正方体的表面积(含孔内各面)是( )
A.258B.234C.222D.210
【答案】B
【分析】先明确题目的含义:正方体共有6个直通小孔,有6个交汇处,计算即可
【详解】正方体无论从哪一个面看,都有两个直通的边长为1的正方形孔,
正方体共有6个直通小孔,有6个交汇处,
表面积等于正方体的表面积减去12个表面上的小正方形面积,
加上6个棱柱的侧面积,减去6个通道的24个小正方形的面积.
则
故选:B.
15.(2024高一下·贵州黔西·期末)端午节吃粽子是中华民族的传统习俗.地区不同,制作的粽子形状也不同,黔西南州最出名的就是鲜肉的灰色粽子,其形状接近于正三棱锥(如图).若正三棱锥的底面边长为2,高为1,则该三棱锥的侧面积为( )
A.B.C.D.
【答案】B
【分析】求出正三棱锥侧面三角形的高即可求解.
【详解】如图,
正三棱锥中,底面,则为正三角形的中心,
连接并延长交于,则为的中点,且,
依题意,,正三角形的边长为2,
所以,,,
,
所以该三棱锥的侧面积为.
故选:B
16.(2024·河南·模拟预测)在正四棱锥中,,若正四棱锥的体积是8,则该四棱锥的侧面积是( )
A.B.C.4D.
【答案】C
【分析】根据棱锥的体积公式,可解得四棱锥的高,然后在直角三角形,由勾股定理可得,进而可得侧面积.
【详解】如图,连接AC,BD,记,连接OP,所以平面ABCD.
取BC的中点E,连接.
因为正四棱锥的体积是8,所以,解得.
因为,所以在直角三角形中,,
则的面积为,
故该四棱锥的侧面积是.
故选:C
17.(2024高三上·辽宁·期末)已知四棱台的上、下底面分别是边长为和的正方形,侧面均为腰长为的等腰梯形,则该四棱台的表面积为( )
A.B.
C.D.
【答案】C
【分析】计算出四棱台侧面的高,再利用梯形和正方形的面积公式可求得该四棱台的表面积.
【详解】设在正四棱台中,取侧面,
则,,,如下图所示:
分别过点、在侧面内作,,垂足分别为、,
因为,,,
所以,,,
因为,,,故四边形为矩形,故,
所以,,,
因此,该四棱台的表面积为.
故选:C.
18.(2024高三上·广东·阶段练习)“李白斗酒诗百篇,长安市上酒家眠”,本诗句中的“斗”的本义是指盛酒的器具,后又作为计量粮食的工具,某数学兴趣小组利用相关材料制作了一个如图所示的正四棱台来模拟“斗”,用它研究“斗”的相关几何性质,已知该四棱台的上、下底的边长分别是2、4,高为1,则该四棱台的表面积为( )
A.B.32C.D.
【答案】C
【分析】根据题意可知:该四棱台的侧面都是上底边长为2,下底边长为4的等腰梯形,
求出侧面的斜高为,然后利用梯形的面积公式即可求出侧面积,进而求解表面积.
【详解】根据题意可知:该四棱台的侧面都是上底边长为2,下底边长为4的等腰梯形,
所以侧面的斜高为,则,
上下底底面面积分别为,
所以该四棱台的表面积为,
故选:.
19.(2024高三上·湖北·开学考试)已知正四棱台上底面边长为2,下底面边长4,高为3,则其表面积为( )
A.36B.
C.D.48
【答案】B
【分析】先求出侧面上的斜高,再求出正四棱台的上、下底面的面积和侧面积,由表面积公式即可得出答案.
【详解】设正四棱台上、下底面的中心为,为侧面上的斜高,
过作交边于点,
所以,
所以,
所以正四棱台的上、下底面的面积为:,
正四棱台的侧面积为:,
则其表面积为:.
故选:B.
20.(2024高一下·全国·课后作业)已知一个圆柱的侧面展开图是一个正方形,则这个圆柱的全面积与侧面积的比是( )
A.B.C.D.
【答案】A
【分析】设侧面展开图正方形边长为,用表示出圆柱底面半径,然后求出全面积与侧面积,再计算比值.
【详解】设正方形边长为,圆柱底面半径为,易知圆柱高为,,,
全面积为,而侧面积为,
所以全面积与侧面积之比这.
故选:A.
21.(2024·广东湛江·二模)如图,将一个圆柱等分切割,再将其重新组合成一个与圆柱等底等高的几何体,越大,重新组合成的几何体就越接近一个“长方体”.若新几何体的表面积比原圆柱的表面积增加了10,则圆柱的侧面积为( )
A.B.C.D.
【答案】A
【分析】新几何体的表面积比原几何体的表面积多了原几何体的轴截面面积,列出方程求解即可.
【详解】显然新几何体的表面积比原几何体的表面积多了原几何体的轴截面面积,
设圆柱的底面半径为,高为,则,
所以圆柱的侧面积为.
故选:A.
22.(2024·福建)以边长为的正方形的一边所在直线为旋转轴,将该正方形旋转一周所得圆柱的侧面积等于
A.B.C.D.
【答案】A
【详解】试题分析:边长为的正方形的一边所在直线为旋转轴,得到的几何体的圆柱,则所得几何体的侧面积为,故选A.
考点:旋转体的概念及侧面积的计算.
23.(2024高三上·全国·阶段练习)已知圆锥的底面半径为2,高为,则该圆锥的侧面积为( )
A.B.C.D.
【答案】B
【分析】由圆锥的侧面展开图扇形基本量与圆锥基本量间的关系可得.
【详解】已知圆锥的底面半径,高,
则母线长,
圆锥的侧面展开图为扇形,且扇形的弧长为圆锥底面圆周长,
扇形的半径为圆锥的母线长,
则圆锥侧面积.
故选:B.
24.(2024·四川成都·二模)若圆锥的表面积为,底面圆的半径为,则该圆锥的高为( )
A.B.C.D.
【答案】B
【分析】利用圆锥的表面积公式可求得圆锥的母线长,再利用勾股定理可求得该圆锥的高.
【详解】设圆锥的母线长为,高为,
则该圆锥的表面积为,解得,
因此,该圆锥的高为.
故选:B.
25.(2024高三上·河南·阶段练习)佛兰德现代艺术中心是比利时洛默尔市的地标性建筑,该建筑是一座全玻璃建筑,整体成圆锥形,它利用现代设计手法令空间与其展示的艺术品无缝交融,形成一个统一的整体,气势恢宏,美轮美英.佛兰德现代艺术中心的底面直径为,侧面积为,则该建筑的高为( )
A.B.C.D.
【答案】C
【分析】已知底面半径和侧面积,可求圆锥母线长,利用勾股定理求圆锥的高.
【详解】设该建筑的母线长为,高为,则由其侧面积为,可得,
解得,所以.
故选:C.
26.(2024高三上·河南·开学考试)圆台轴截面面积为,上下底面半径之比为,母线与底面所成角为,则圆台侧面积为( )
A.B.
C.D.
【答案】C
【分析】作出轴截面,利用等腰梯形面积公式求出上下底面半径和母线长,再利用圆台侧面积公式即可得到答案.
【详解】作出轴截面,则四边形为等腰梯形,,
过点作,
设上底面半径长为,则下底面半径长为,
则上底面直径,下底面直径,
则,则,
则,解得,
则上底面半径,下底面半径,
母线,则圆台侧面积.
故选:C.
27.(2024高二上·江苏镇江·开学考试)已知圆台的上下底面半径分别为2和5,且母线与下底面所成为角的正切值为,则该圆台的表面积为( )
A.B.C.D.
【答案】D
【分析】根据圆台的轴截面,结合正切函数的定义、圆台表面积公式进行求解即可.
【详解】如图所示圆台的轴截面,
过点作,
因此有,
因为母线与下底面所成为角的正切值为,
所以,
该圆台的表面积为,
故选:D
28.(2024·甘肃兰州·模拟预测)攒尖是中国古建筑中屋顶的一种结构形式,常见的有圆形攒尖、三角攒尖、四角攒尖、六角攒尖等,多见于亭阁式建筑,兰州市著名景点三台阁的屋顶部分也是典型的攒尖结构.如图所示是某研究性学习小组制作的三台阁仿真模型的屋顶部分,它可以看作是不含下底面的正四棱台和正三棱柱的组合体,已知正四棱台上底、下底、侧棱的长度(单位:dm)分别为2,6,4,正三棱柱各棱长均相等,则该结构表面积为( )
A.B.C.D.
【答案】A
【分析】根据三棱柱和棱台表面积公式计算即可.
【详解】由题可得正三棱柱的底面积为:,
正三棱柱的外露表面积为:,
四棱台侧面梯形的高为:,
四棱台外露表面积为:,
该结构表面积为:.
故选:A
29.(2024高三上·黑龙江哈尔滨·期中)正三棱柱侧面的一条对角线长为2,且与底面成角,则此三棱柱的体积为( )
A.B.C.D.
【答案】D
【分析】根据题意,得到底面,得到为与底面所成的角,进而求得三棱柱的底面边长和侧棱长,结合体积公式,即可求解.
【详解】如图所示,设正三棱柱的底面边长为,侧棱长为,
由正三棱柱中,底面,
所以为与底面所成的角,所以,
因为,所以,
即正三棱柱的底面边长为,侧棱长为,
所以三棱柱的体积为.
故选:D.
30.(2008·四川)若三棱柱的一个侧面是边长为2的正方形,另外两个侧面都是有一个内角为的菱形,则该棱柱的体积等于
A.B.C.D.
【答案】B
【详解】
如图在三棱柱中,设,
由条件有,作
AO⊥面于点,
则
∴ ∴
∴ 故选B
【点评】:此题重点考察立体几何中的最小角定理和柱体体积公式,同时考察空间想象能力;
【突破】:具有较强的空间想象能力,准确地画出图形是解决此题的前提,熟悉最小角定理并能准确应用是解决此题的关键;
31.(2024高三上·河南焦作·开学考试)把过棱锥的顶点且与底面垂直的直线称为棱锥的轴,过棱锥的轴的截面称为棱锥的轴截面.现有一个正三棱锥、一个正四棱锥、一个正六棱锥,它们的高相等,轴截面面积的最大值也相等,则此正三棱锥、正四棱锥、正六棱锥的体积之比为( )
A.B.
C.D.
【答案】C
【分析】根据正三棱锥、正四棱锥、正六棱锥的结构特征,结合空间直观想象找到底面边长与高、最大轴截面的等量关系,都用表示边长,进而代入分别求解体积,得到体积之比.
【详解】设3个正棱锥的高均为h,轴截面面积的最大值均为S.
(1)正三棱锥
当轴截面与底面的一条棱垂直时,轴截面面积最大,
如图,设正三棱锥的底面边长为a,取底边的中点,
则,平面VAD,故平面,
即为面积最大的轴截面图形.
所以,即,
可得正三棱锥的体积为.
(2)正四棱锥
当轴截面经过底面的一条对角线时,轴截面面积最大,
如图,设正四棱锥的底面边长为b,
连接,即为面积最大的轴截面图形.
所以,即,
则底面的面积为,
可得正四棱锥的体积为.
(3)正六棱锥
当轴截面经过底面的两个相对的顶点时,轴截面面积最大,
如图,设正六棱锥的底面边长为c,
连接,即为面积最大的轴截面图形.
所以,则,
可得正六棱锥的体积为
.
所以正三棱锥、正六棱锥的体积之比为,即.
故选:C.
32.(2024·广东深圳·二模)设表面积相等的正方体、正四面体和球的体积分别为、和,则( )
A.B.C.D.
【答案】B
【分析】设正方体棱长为,正四面体棱长为,球的半径为,面积为.表示出3个几何体的表面积,得出,进而求出体积的平方,比较体积的平方大小,然后得出答案.
【详解】设正方体棱长为,正四面体棱长为,球的半径为,面积为.
正方体表面积为,所以,
所以,;
如图,正四面体,为的中点,为的中心,则是底面上的高.
则,,所以,
所以,
所以,正四面体的表面积为,所以.
又为的中心,所以.
又根据正四面体的性质,可知,
所以,
所以,;
球的表面积为,所以,
所以,.
因为,
所以,,
所以,.
故选:B.
33.(2024·河南郑州·模拟预测)《九章算术·商功》:“斜解立方,得两堑堵,斜解堑堵,其一为阳马,其一为鳖臑”.意思是一个长方体沿对角面斜解(图1),得到一模一样的两个堑堵(图2),再沿一个堑堵的一个顶点和相对的棱斜解(图2),得一个四棱锥称为阳马(图3),一个三棱锥称为鳖臑(图4).若长方体的体积为,由该长方体斜解所得到的堑堵、阳马和鳖臑的体积分别为,,,则下列等式错误的是( )
A.B.
C.D.
【答案】B
【分析】根据题设得,,再分析阳马与鳖臑的体积数量关系,即可判断各项正误.
【详解】由题设,,,则,A对;
如下图,连接,将阳马一分为二,又,
所以,,则,故,
所以B错,C、D对.
故选:B
34.(2024高三下·浙江杭州·阶段练习)已知矩形中,,,是的中点,沿直线将△翻折成△,则三棱锥的体积的最大值为( )
A.B.C.D.
【答案】B
【分析】当平面平面,此时点到平面的距离取得最大值,取的中点,得到,证得平面,得到三棱锥的高为,结合体积公式,即可求解.
【详解】如图所示,要使得三棱锥的体积取得最大值,
当平面平面,此时点到平面的距离取得最大值,
取的中点,因为,可得,
因为平面平面,且平面,所以平面,
在直角中,可得,即三棱锥的高为,
又由三角形的面积为,
所以三棱锥的体积的最大值.
故选:B.
35.(2024·全国)正四棱台的上、下底面的边长分别为2,4,侧棱长为2,则其体积为( )
A.B.C.D.
【答案】D
【分析】由四棱台的几何特征算出该几何体的高及上下底面面积,再由棱台的体积公式即可得解.
【详解】作出图形,连接该正四棱台上下底面的中心,如图,
因为该四棱台上下底面边长分别为2,4,侧棱长为2,
所以该棱台的高,
下底面面积,上底面面积,
所以该棱台的体积.
故选:D.
36.(2024高一下·江苏连云港·阶段练习)在《九章算术商功》中将正四面形棱台体棱台的上、下底面均为正方形称为方亭.在方亭中,,四个侧面均为全等的等腰梯形且面积之和为,则该方亭的体积为( )
A.B.C.D.
【答案】D
【分析】先根据方亭四个侧面的面积之和得到的长度,然后作辅助线找到并求方亭的高,最后利用棱台的体积计算公式求解即可.
【详解】如图,过作,垂足为,
由四个侧面的面积之和为知,侧面的面积为,
(梯形的面积公式),则.
由题意得:,在中,.
连接,,过作,垂足为,
易知四边形为等腰梯形且,,则,
,
该方亭的体积,(棱台的体积公式).
故选:D.
37.(2024高三上·山西运城·期中)已知一个正四棱台的上下底面边长为、,侧棱长为,则棱台的体积为( )
A.B.C.D.
【答案】D
【分析】根据正四棱台的概念可知四边形为等腰梯形,进而可得四棱台的高,即可求得体积.
【详解】
如图所示,
由正四棱台可知,四边形为等腰梯形,
且,,,
所以,
所以,
故选:D.
38.(2024·河南·模拟预测)光岳楼,又称“余木楼”“鼓楼”“东昌楼”,位于山东省聊城市,在《中国名楼》站台票纪念册中,光岳楼与鹳雀楼、黄鹤楼、岳阳楼、太白楼、滕王阁、蓬莱阁、镇海楼、甲秀楼、大观楼共同组成中国十大名楼.其墩台为砖石砌成的正四棱台,如图所示,光岳楼的墩台上底面正方形的边长约为32m,下底面正方形的边长约为34.5m,高的4倍比上底面的边长长4m,则光岳楼墩台的体积约为( )
A.B.C.D.
【答案】B
【分析】根据题意,求得光岳楼墩台的高,结合台体的体积公式,即可求解.
【详解】由题意,设光岳楼墩台的高为h,则,
所以光岳楼墩台的体积约为.
故选:B.
39.(四川省仁寿第一中学校(北校区)2023-2024学年高三上学期9月月考文科数学试题)已知圆柱的高为1,它的两个底面的圆周在直径为2的同一个球的球面上,则该圆柱的体积为( )
A.B.C.D.
【答案】C
【分析】设圆柱的底面半径为,利用勾股定理求出,再根据圆柱的体积公式计算可得.
【详解】设圆柱的底面半径为,则,解得或(舍去),
所以圆柱的体积.
故选:C
40.(2024高三上·江苏苏州·开学考试)若某圆柱体的底面半径与某球体的半径相等,圆柱体与球体的体积之比和它们的表面积之比的比值相等,则该圆柱体的高与球体的半径的比值为( )
A.B.C.D.2
【答案】D
【分析】由圆柱与球的表面积公式和体积公式列比例式求解.
【详解】设圆柱底面半径为r,则球的半径为r,设圆柱的高为h,
,,,,
∴,∴,
故选:D
41.(2024·河南·模拟预测)圆锥的高为2,其侧面展开图的圆心角为,则该圆锥的体积为( ).
A.B.C.D.
【答案】B
【分析】根据题意,求得圆锥的高,再由圆锥的体积公式,即可得到结果.
【详解】设圆锥的底面半径为r,母线长为l,高为h,则,
所以,,
所以圆锥的体积为.
故选:B
42.(2024高三上·福建厦门·阶段练习)已知母线长为5的圆锥的侧面积为,则这个圆锥的体积为( )
A.B.C.D.
【答案】A
【分析】求出底面半径和高后,由体积公式计算.
【详解】设圆锥的高为,底面半径为,则
,,∴,
体积为,
故选:A.
43.(2024高三下·河南开封·阶段练习)木桶作为一种容器,在我国使用的历史已经达到了几千年,其形状可视为一个圆台.若某圆台形木桶上、下底面的半径分别为,母线长为,木板厚度忽略不计,则该木桶的容积为( )
A.B.C.D.
【答案】D
【分析】作出图象,求出圆台的高,再根据体积公式求解即可.
【详解】解:如图所示:
由题意可知此圆台的高,
所以此圆台的体积.
故选:D.
44.(2024高三上·福建厦门·阶段练习)用一个平行于圆锥底面的平面截该圆锥得到一个圆台,若圆台上底面和下底面半径之比为,则该圆台与圆锥的体积之比为( )
A.B.C.D.
【答案】C
【分析】设圆台的上底面半径为,截去的小圆锥的高为,可得圆锥下底面半径为,圆锥的高为,求出圆台与圆锥的体积可得答案.
【详解】设圆台的上底面半径为,截去的小圆锥的高为,
可得圆锥下底面半径为,圆锥的高为,
所以圆锥的体积为,小圆锥的体积为,
所以圆台的体积为,
所以该圆台与圆锥的体积之比为.
故选:C.
二、多选题
45.(2024·全国)如图,四边形为正方形,平面,,记三棱锥,,的体积分别为,则( )
A.B.
C.D.
【答案】CD
【分析】直接由体积公式计算,连接交于点,连接,由计算出,依次判断选项即可.
【详解】
设,因为平面,,则,
,连接交于点,连接,易得,
又平面,平面,则,又,平面,则平面,
又,过作于,易得四边形为矩形,则,
则,,
,则,,,
则,则,,,故A、B错误;C、D正确.
故选:CD.
46.(2024·福建·模拟预测)等腰梯形的上下底边之比为,若绕该梯形的对称轴旋转一周所得几何体的表面积为,则该梯形的周长可能为( )
A.B.8C.D.16
【答案】CD
【分析】设圆台上下底面半径分别为,,母线长,根据圆台表面积公式得,结合基本不等式可求该梯形的周长得最小值,从而可得答案.
【详解】等腰梯形绕对称轴旋转一周所得几何体是圆台,设其上下底面半径分别为,,母线长,
则表面积,由此得,
于是梯形周长,
当且仅当时取等号,故则该梯形的周长最小值为.
故选:CD.
47.(2024·河南·模拟预测)如图,正三棱柱的底面边长为1,高为3,为棱的中点,分别在棱上,且满足取得最小值.记四棱锥、三棱锥的体积分别为,则( )
A.B.C.D.
【答案】ABD
【分析】根据三棱柱的体积公式即可判断A,根据平面展开图可得线段最短时,即可根据锥体体积公式判断BCD.
【详解】正三棱柱的体积为,由图可知,所以,所以A正确;
沿着侧棱将棱柱展开得到一个矩形,连接,
因为取得最小值,即线段,
由于四边形为边长为3的正方形,所以,因为为的中点,所以
,,
,所以B正确,C不正确,D正确.
故选:ABD.
48.(2024高三上·湖南·阶段练习)若某正方体的棱长为,则( )
A.该正方体的体积为5B.该正方体的内切球的体积为
C.该正方体的表面积为30D.该正方体的外接球的表面积为
【答案】BCD
【分析】根据正方体的体积表面积公式即可求解AC,根据内切球和外接球的直径即可得半径,由球的体积公式以及表面积公式求解BD.
【详解】因为该正方体的棱长为,所以其体积为,表面积为,A错误,C正确.
该正方体的内切球的直径为,所以内切球的体积为,B正确.
该正方体的外接球的直径为正方体的体对角线长,所以外接球的表面积为,D正确.
故选:BCD
三、填空题
49.(2024·辽宁锦州·模拟预测)已知用斜二测画法画梯形OABC的直观图如图所示,,,,轴,,为的三等分点,则四边形OABC绕y轴旋转一周形成的空间几何体的体积为 .
【答案】
【分析】先由直观图还原梯形,再利用斜二测画法的性质求得其边与高,从而判断得该梯形为等腰梯形,进而利用圆台与圆锥的体积公式求解即可.
【详解】在直观图中,,所以在还原图中,,如图,
在直观图中,,为的三等分点,
所以在还原图中,,D为OA的三等分点,
又在直观图中,轴,
所以在还原图中,轴,则,
所以,则,
故,,所以四边形OABC是等腰梯形,
所以四边形OABC绕y轴旋转一周所形成的空间几何体的体积等于一个圆台的体积减去一个圆锥的体积,
即.
故答案为:.
50.(2024高三·全国·对口高考)若正用斜二测画法画出的水平放置图形的直观图为,当的面积为时,的面积为 .
【答案】
【分析】根据题意画出图形,由直观图作图规则,结合图形根据的面积求出的面积.
【详解】是正的斜二测画法的水平放置图形的直观图,如图所示,
设,
则的面积为,,
的面积为.
故答案为:.
51.(2024高三下·上海宝山·开学考试)我们知道一条线段在“斜二测”画法中它的长度可能会发生变化的,现直角坐标系平面上一条长为4cm线段AB按“斜二测”画法在水平放置的平面上画出为,则最短长度为 cm(结果用精确值表示)
【答案】
【分析】假设A与坐标原点重合,,根据斜二测画法的规则求出点的坐标,进而表示出的长度,即可得解.
【详解】假设A与坐标原点重合,,
则可得在斜二测画法下的坐标为,
所以
,
所以最短长度为.
故答案为:.
52.(2024高三·全国·阶段练习)如图,梯形ABCD是水平放置的一个平面图形的直观图,其中,,,则原图形的面积为 .
【答案】
【分析】根据水平放置的平面图形直观图画法画出原图计算可得答案.
【详解】因为,, ,
所以,,
所以.
故答案为:.
53.(2024高三上·上海普陀·期中)2022年4月16日,神舟十三号载人飞船返回舱在东风着陆场预定区域成果着陆.如图,在返回过程中使用的主降落伞外表面积达到1200平方米,若主降落伞完全展开后可以近似看着一个半球,则完全展开后伞口的直径约为 米(精确到整数)
【答案】28
【分析】根据球体的表面积公式,结合题意,直接求解即可.
【详解】设主降落伞展开后所在球体的半径为,由题可得,解得,
故完全展开后伞口的直径约为米.
故答案为:.
54.(2024高一下·四川成都·阶段练习)已知圆锥的底面半径为1,其侧面展开图为一个半圆,则该圆锥的体积为 .
【答案】/
【分析】先计算圆锥的底面周长,即为侧面展开图的弧长,进而求得侧面展开图的半径,即为圆锥的母线长,再求得圆锥的高,从而求得体积即可
【详解】∵圆锥的底面半径为1,∴侧面展开图的弧长为,
又∵侧面展开图是半圆,∴侧面展开图的半径为2,即圆锥的母线长为2,故圆锥的高为,故体积
故答案为:
55.(2024·安徽·模拟预测)如图,在三棱锥P-ABC的平面展开图中,,,,,,则三棱锥外接球表面积为 .
【答案】14π
【分析】由余弦定理及勾股定理求出相关边长,从而可确定球心及半径,进一步可得答案.
【详解】由题意可知,,,,,
在BCF中,,则,
因为,所以,
在三棱锥P-ABC外接球的球心为O,,,记PA中点为O,,即三棱锥P-ABC外接球的球心为点O,
半径,所以外接球表面积为14π.
故答案为:14π
56.(2024·安徽马鞍山·模拟预测)已知三棱锥P-ABC的底面ABC为等边三角形.如图,在三棱锥P-ABC的平面展开图中,P,F,E三点共线,B,C,E三点共线,,,则PB= .
【答案】
【分析】根据的余弦值,求出正弦值,由正弦定理得到PF,进而由余弦定理求出EF和PB.
【详解】由题意可知,△CEF为等边三角形,所以,则,
由可知,
在△PCF中,由正弦定理得:.
在△PCE中,由余弦定理得:,
解得或(舍去),
所以,
则,,
在△PBE中,由余弦定理得,
所以.
故答案为:
57.(2024高三上·山西大同·阶段练习)如图,在三棱锥的平面展开图中,,,,,,则三棱锥的外接球的表面积为 .
【答案】
【分析】根据展开图还原出几何体,画出图形,即可根据正余弦定理求出相关量,进而求出球半径,得出表面积.
【详解】还原出如图所示的三棱锥,
,,平面,
设平面的截面圆心为,半径为,球心为,球半径为,
在中,由余弦定理可得,则,
这由正弦定理得,,
,
,
外接球的表面积.
故答案为:.
【点睛】本题考查几何体外接球表面积的计算,涉及到正余弦定理的应用,涉及线面垂直关系,属于中档题.
58.(2024高三·河北·专题练习)如图,正方体的棱长为,点为的中点,在对角面上取一点,使最小,其最小值为
【答案】
【分析】取中点,根据正方体对称关系可知,可得,利用勾股定理求得,从而得到结果.
【详解】取中点,连接
则
(当且仅当三点共线时取等号)
又
的最小值为:
故答案为:
59.(2024高三上·四川成都·开学考试)如图一个正六棱柱的茶叶盒,底面边长为,高为,则这个茶叶盒的表面积为 .
【答案】
【分析】根据棱柱表面积的求法,结合已知求茶叶盒的表面积.
【详解】由题设,一个底面的面积为,
一个侧面矩形面积为,
所以茶叶盒的表面积为.
故答案为:
60.(2024高二上·上海黄浦·阶段练习)若长方体的对角线的长为,其长、宽、高的和是,则长方体的全面积是 .
【答案】
【分析】设长方体的长、宽、高分别为,利用可构造方程求得,即为所求的全面积.
【详解】设长方体的长、宽、高分别为,则,
,
,即长方体的全面积为.
故答案为:.
61.(2024·全国·模拟预测)正四棱锥P-ABCD的各条棱长均为2,则该四棱锥的表面积为 .
【答案】
【分析】分别求出底面积和侧面积,即可求出表面积.
【详解】因为正四棱锥P-ABCD的各条棱长均为2,
所以正四棱锥的底面积为,侧面积为,
所以该四棱锥的表面积为.
故答案为:
62.(2024高三·全国·专题练习)一个正三棱台的上、下底面边长分别是3 cm和6 cm,高是cm.则三棱台的斜高为 ;三棱台的侧面积为 ;表面积为 .
【答案】
【分析】设O1、O分别为正三棱台ABC—A1B1C1的上、下底面正三角形的中心,作出斜高,然后结合图形根据面积公式求解可得.
【详解】设O1、O分别为正三棱台ABC—A1B1C1的上、下底面正三角形的中心,如图所示,则O1O=,过O1作O1D1⊥B1C1,OD⊥BC,则D1D为三棱台的斜高;
过D1作D1E⊥AD于E,则D1E=O1O=,
因,
则DE=OD-O1D1=.
在Rt△D1DE中,D1D= (cm).
故三棱台斜高为cm.
设c、c′分别为上、下底的周长,h′为斜高,
S侧=(c+c′)h′=(3×3+3×6)×=(cm2),
S表=S侧+S上+S下=+(cm2).
故三棱台的侧面积为cm2,表面积为cm2.
故答案为:,,
63.(2024高三·全国·专题练习)若矩形的周长为36,矩形绕它的一条边旋转形成一个圆柱,求圆柱侧面积的最大值为 .
【答案】
【分析】利用基本不等式及圆柱的侧面积计算公式即可得出.
【详解】如图所示,不妨设矩形的长与宽分别为,,
旋转形成的圆柱的底面半径为,母线长,
则,即,
,得,当且仅当时取等号,
旋转形成的圆柱的侧面积,
旋转形成的圆柱的侧面积的最大值为.
故答案为:.
64.(2024高二上·北京海淀·期中)若一个圆锥的轴截面是等边三角形,其面积为,则这个圆锥的侧面积是 .
【答案】
【分析】设母线为,底面半径为,即可得到且,从而求出、,再根据侧面积公式计算可得.
【详解】解:由题意圆锥的轴截面是等边三角形,其面积为,设母线为,底面半径为,则,且,
,,,
所以圆锥的侧面积.
故答案为:.
65.(2024高三上·全国·专题练习)某地球仪上北纬纬线的长度为,该地球仪的半径是 cm,
表面积是 cm2.
【答案】 ; .
【分析】先利用圆周长公式,求出小圆的半径,根据球的截面性质,可求出球的半径,进而求出球的表面积.
【详解】设北纬所在圆面的关系为,由题可得:解得,设地球仪的半径为,地球仪表面积为.
【点睛】本题考查了纬度的定义、球的表面积公式,考查了球的截面性质.
66.(2024·全国)已知圆和圆是球的大圆和小圆,其公共弦长等于球的半径,,且圆与圆所在的平面所成的一个二面角为则球的表面积等于 .
【答案】
【分析】设为两圆的公共弦,为的中点,由题可得,然后利用球的性质结合条件可得球的半径,进而利用球的表面积公式即得.
【详解】如图,设为两圆的公共弦,为的中点,连接,则
结合题意可知,
设球的半径为,则,为正三角形.。
∴,又,
∴,
∴,
∴球的表面积等于.
故答案为:.
67.(2009年普通高等学校招生全国统一考试理科数学(全国卷Ⅱ))设OA是球O的半径,M是OA的中点,过M且与OA成角的平面截球O的表面得到圆C.若圆C的面积等于,则球O的表面积等于
【答案】8
【详解】试题分析:设球半径为R,圆C的半径为r,
由 ,得.
因为.
由,得
故球的表面积等于8π
考点:球的体积和表面积
点评:本题考查学生的空间想象能力,以及球的面积体积公式的应用,是基础题.
68.(2024·全国)用平面截半径为的球,如果球心到截面的距离为,那么截得小圆的面积与球的表面积的比值为 .
【答案】
【分析】利用球的半径,球心到截面的距离,求出小圆半径,再求小圆面积;进而可求出球的表面积,然后可得比值.
【详解】解:小圆半径是:,小圆的面积是:,
球的表面积是;
截得小圆的面积与球的表面积的比值为:
故答案为:
69.(2024高三上·广东广州·阶段练习)陀螺是中国民间较早的娱乐工具之一,也称陀罗,图l是一种木陀螺,可近似地看作是一个圆锥和一个圆柱的组合体,其直观图如图2所示,其中A是圆锥的顶点,B,C分别是圆柱的上、下底面圆的圆心,且,,底面圆的半径为1,则该陀螺的表面积是 .
【答案】
【分析】根据题意,求出圆锥的侧面积和圆柱的侧面积,从而求得该陀螺的表面积,得到答案.
【详解】因为陀螺的底面圆的半径为,
由,则,即圆柱的母线长为,
所以圆锥的母线长为,则圆锥的侧面积为,
圆柱的侧面积为,圆柱的底面积为,
所以该陀螺的表面积为.
故答案为:.
70.(2024高三·全国·专题练习)如图,八面体的每一个面都是正三角形,并且4个顶点A,B,C,D在同一个平面内.如果四边形ABCD是边长为30 cm的正方形,那么这个八面体的表面积是 .
【答案】
【分析】求出每个面的面积即可求得表面积.
【详解】因为八面体的每一个面都是正三角形,且四边形ABCD是边长为的正方形,
所以每个面的面积为(),
则这个八面体的表面积().
故答案为:
71.(2024高三上·天津北辰·阶段练习)已知一个圆柱的高是底面半径的2倍,且其上、下底面的圆周均在球面上,若球的体积为,则圆柱的体积为 .
【答案】/
【分析】由题先求得球的半径,再根据的数量关系,即可求得圆柱的体积.
【详解】设球的半径为,圆柱的底面圆半径为,则高为.
因为球的体积为,所以,得,
又因为,所以,
所以,圆柱的体积
故答案为:
72.(2024高三上·云南昆明·阶段练习)已知某圆锥的侧面展开图是一个半径为的半圆、则该圆锥的体积为 .
【答案】
【分析】设圆锥的高为,底面圆的半径为,则,根据圆锥的底面圆周长等于侧面展开图的弧长,求出 ,最后根据圆锥的体积公式即可得出答案.
【详解】解:设圆锥的高为,底面圆的半径为,则,由题意可知半圆的弧长为,所以,,
所以,所以圆锥体积.
故答案为: .
73.(2024·浙江嘉兴·模拟预测)已知圆锥的底面半径为1,侧面积为,则此圆锥的体积是 .
【答案】
【分析】由圆锥的侧面积公式可求出母线长,再求出圆锥的高,由圆锥的体积公式即可得出答案.
【详解】设圆锥的高为,母线长为,半径,
因为圆锥的底面半径为1,侧面积为,
所以,所以,
所以,
所以圆锥的体积是.
故答案为:.
74.(2024高三上·广东广州·阶段练习)已知圆锥的底面半径为2,侧面展开图是一个圆心角为120°的扇形.把该圆锥截成圆台,已知圆台的下底面与该圆锥的底面重合,圆台的上底面半径为1,则圆台的体积为 .
【答案】
【分析】由已知求出圆锥的高,进而求出截去的小圆锥的高,利用大圆锥体积减去小圆锥体积求圆台体积即可.
【详解】设圆锥母线长为,则,故圆锥的高为,
由圆台的上底面半径为1,故截去的小圆锥的高为,
所以圆台体积为.
故答案为:
成套的课件成套的教案成套的试题成套的微专题尽在高中数学同步资源大全QQ群552511468也可联系微信fjshuxue加入百度网盘群1.5T一线老师必备资料一键转存自动更新永不过期
名称
棱柱
棱锥
棱台
图形
底面
互相平行且全等
多边形
互相平行且相似
侧棱
平行且相等
相交于一点但不一定相等
延长线交于一点
侧面形状
平行四边形
三角形
梯形
名称
圆柱
圆锥
圆台
球
图形
母线
互相平行且相等,垂直于底面
相交于一点
延长线交于一点
轴截面
矩形
等腰三角形
等腰梯形
圆
侧面展开图
矩形
扇形
扇环
圆柱
圆锥
圆台
侧面展开图
侧面积公式
S圆柱侧=2πrl
S圆锥侧=πrl
S圆台侧=π(r1+r2)l
名称
几何体
表面积
体积
柱体
S表=S侧+2S底
V=Sh
锥体
S表=S侧+S底
V=eq \f(1,3)Sh
台体
S表=S侧+S上+S下
V=eq \f(1,3)(S上+S下+eq \r(S上S下))h
球
S表=4πR2
V=eq \f(4,3)πR3
(一)
1.空间几何体结构特征的判断技巧
(1)说明一个命题是错误的,只要举出一个反例即可.
(2)在斜二测画法中,平行于x轴的线段平行性不变,长度不变;平行于y轴的线段平行性不变,长度减半.
(3)在解决空间折线(段)最短问题时一般考虑其展开图,采用化曲为直的策略,将空间问题平面化.
2.多面体表面展开图可以有不同的形状,应多实践,观察并大胆想象立体图形与表面展开图的关系,一定先观察立体图形的每一个面的形状.
3.最大路径问题:大胆展开,把问题变为平面两点间线段最短问题.
题型1:基本立体图形结构特征
1-1.(2024·新疆·模拟预测)下列命题中正确的是( )
A.有两个平面平行,其余各面都是平行四边形的几何体是棱柱.
B.各个面都是三角形的几何体是三棱锥.
C.夹在圆柱的两个平行截面间的几何体还是一个旋转体.
D.圆锥的顶点与底面圆周上任意一点的连线都是母线.
【答案】D
【分析】根据空间几何体的定义判断.
【详解】如图所示的几何体满足两个平面平行,其余各面都是平行四边形,但它不是棱柱,A错;
正八面体的各面都是三角形,不是三棱锥,B错;
如果两个平行截面与圆柱的底面平行,则是旋转体,如果这两个平行截面与圆柱的底面不平行,则不是旋转体.C错;
根据圆锥的定义,D正确.
故选:D.
1-2.(2024高一·全国·课后作业)下列命题:
①有两个面平行,其他各面都是平行四边形的几何体叫做棱柱;
②有两侧面与底面垂直的棱柱是直棱柱;
③过斜棱柱的侧棱作棱柱的截面,所得图形不可能是矩形;
④所有侧面都是全等的矩形的四棱柱一定是正四棱柱.
其中正确命题的个数为( )
A.0B.1C.2D.3
【答案】A
【分析】①②③④均可举出反例.
【详解】①如图1,满足有两个面平行,其他各面都是平行四边形,
显然不是棱柱,故①错误;
②如图2,满足两侧面与底面垂直,但不是直棱柱,②错误;
③如图3,四边形为矩形,
即过斜棱柱的侧棱作棱柱的截面,所得图形可能是矩形,③错误;
④所有侧面都是全等的矩形的四棱柱不一定是正四棱柱,因为两底面不一定是正方形,④错误.
故选:A
1-3.(2024高一下·山西吕梁·期末)下列说法正确的是( )
A.三角形的直观图是三角形B.直四棱柱是长方体
C.平行六面体不是棱柱 D.两个平面平行,其余各面是梯形的多面体是棱台
【答案】A
【分析】对A,根据直观图的定义判断;对B,直四棱柱可能底面不是矩形,结合长方体定义即可判断;对C,结合棱柱定义,平行六面体是四棱柱,即可判断;对D,结合棱台侧棱延长后需要交于一点,即可判断
【详解】对A,根据直观图的定义,三角形的直观图是三角形,故A对;
对B,底面是长方形的直四棱柱是长方体,故B错;
对C,平行六面体一定是棱柱,故C错;
两个平面平行,其余各面是梯形的多面体,当侧棱延长后不交于同一点时,不是棱台,故D错;
故选:A
1-4.(2024高三·全国·专题练习)给出下列命题:
①在圆柱的上、下底面的圆周上各取一点,则这两点的连线是圆柱的母线;
②直角三角形绕其任一边所在直线旋转一周所形成的几何体都是圆锥;
③棱台的上、下底面可以不相似,但侧棱长一定相等.
其中正确命题的个数是( )
A.B.C.D.
【答案】A
【分析】根据圆柱母线的定义可判断命题①的正误;根据圆锥的形成可判断命题②的正误;根据棱台的定义可判断命题③的正误.
【详解】①不一定,只有当这两点的连线平行于轴时才是母线;
②不一定,当以斜边所在直线为旋转轴时,其余两边旋转形成的面所围成的几何体不是圆锥,如图所示,它是由两个同底圆锥组成的几何体;
③错误,棱台的上、下底面相似且是对应边平行的多边形,各侧棱延长线交于一点,但是侧棱长不一定相等.
故选:A.
【点睛】本题考查几何体结构特征的判断,属于基础题.
题型2:直观图
2-1.(2024高一下·浙江宁波·期中)用斜二测画法画出的某平面图形的直观图如图所示,边与平行于轴.已知四边形的面积为,则原平面图形的面积为 .
【答案】
【分析】作出原图形,根据原图形与直观面积之间的关系求解.
【详解】根据题意得,原四边形为一个直角梯形,
且,,,
,
则,
所以,.
故答案为:.
2-2.(2024高一下·上海奉贤·期末)如图,是用斜二测画法得到的△AOB的直观图,其中则AB的长度为 .
【答案】
【分析】把直观图还原为原平面图形,根据直观图画法规则,利用勾股定理求出AB的长度即可.
【详解】把直观图还原为,如图所示:
根据直观图画法规则知,,
所以的长度为.
故答案为:.
2-3.(2024高一上·山东济宁·阶段练习)有一块多边形的菜地,它的水平放置的平面图形的斜二测直观图是直角梯形(如图所示).,则这块菜地的面积为
【答案】
【分析】利用直观图中的信息,求出的长度,从而得到原平面图形中的长度,利用梯形的面积公式求解即可.
【详解】
过作于,
在直观图中,,,,
所以,,
故原平面图形的上底为 ,下底,高为,
所以这块菜地的面积为,
故答案为:.
2-4.(2024高二上·宁夏石嘴山·阶段练习)如图,用斜二测画法画一个水平放置的平面图形的直观图为一个正方形,则原来图形的面积是 .
【答案】
【分析】根据斜二测画法的过程把给出的直观图还原回原图形,再利用斜二测画法的特点及平行四边形的面积公式即可求解.
【详解】由直观图可知,在直观图中,正方形的对角线长为,由斜二测画法的特点,知该平面图形的直观图的原图形如图所示
所以原图图形为平行四边形,底面边长为,位于轴的对角线长为,
所以原来图形的面积为.
故答案为:.
题型3:展开图
3-1.(2024·山东青岛·三模)已知圆锥的底面半径为1,侧面展开图为半圆,则该圆锥内半径最大的球的表面积为 .
【答案】/
【分析】由圆锥侧面展开图求得圆锥母线长,圆锥内半径最大的球与圆锥相切,作出圆锥的轴截面,截球得大圆为圆锥轴截面三角形的内切圆,由此图形计算出球的半径后可得表面积.
【详解】设圆锥母线长为,由题意,,
圆锥内半径最大的球与圆锥相切,
作出圆锥的轴截面,截球得大圆为圆锥轴截面三角形的内切圆,是切点,如图,易知是圆锥的高,在上,
由得,因此,所以,
,
所以圆锥内半径最大的球的表面积为,
故答案为:.
3-2.(2024高二下·云南红河·阶段练习)如图,在直三棱柱的侧面展开图中,B,C是线段AD的三等分点,且.若该三棱柱的外接球O的表面积为12π,则 .
【答案】
【分析】根据正三棱柱得性质,确定外接球的球心,利用球的表面积公式以及勾股定理,可得答案.
【详解】由该三棱柱的外接球O的表面积为12π,设外接球得半径为,则,解得,
由题意,取上下底面三角形得中心,分别为,得中点即为外接圆圆心,作图如下:
则,平面,,
平面,,
在等边中,,
在中,,
.
故答案为:.
3-3.(2024·安徽黄山·一模)如图,在四棱锥P-ABCD的平面展开图中,正方形ABCD的边长为4,是以AD为斜边的等腰直角三角形,,则该四棱锥外接球被平面PBC所截的圆面的面积为 .
【答案】
【分析】先由线面垂直判定定理证明平面,进而建立空间直角坐标系,根据球心的性质列出方程得出球心坐标,再求出平面的法向量,最后由向量法得出四棱锥外接球的球心到面的距离,再计算出半径即可求解.
【详解】该几何体的直观图如下图所示
分别取的中点,连接
又,所以由线面垂直的判定定理得出平面
以点为坐标原点,建立空间直角坐标系
,
设四棱锥外接球的球心
,,解得
设平面的法向量为
,取,则
四棱锥外接球的球心到面的距离为
又,所以平面PBC所截的圆的半径
所以平面PBC所截的圆面的面积为.
故答案为:
题型4:最短路径问题
4-1.(2024高三·全国·专题练习)如图,一竖立在地面上的圆锥形物体的母线长为4,一只小虫从圆锥的底面圆上的点P出发,绕圆锥爬行一周后回到点P处,若该小虫爬行的最短路程为,则这个圆锥的体积为( ).
A.B.C.D.
【答案】C
【分析】作出该圆锥的侧面展开图,该小虫爬行的最短路程为,由余弦定理求出.求出底面圆的半径r,从而求出这个圆锥的高,由此能求出这个圆锥的体积.
【详解】作出该圆锥的侧面展开图,如图所示:
该小虫爬行的最短路程为,
由余弦定理可得,.设底面圆的半径为r,
则有,解得.∴这个圆锥的高为,
这个圆锥的体积为.
故选:C.
4-2.(2024高一下·河南开封·期中)如图,已知正四棱锥的侧棱长为,侧面等腰三角形的顶角为,则从A点出发环绕侧面一周后回到A点的最短路程为( )
A.B.C.D.6
【答案】D
【分析】把正四棱锥的侧面沿着SA剪开,得到它的侧面展开图,得到一个由四个全等的顶角为的等腰三角形组成的图象,所求的路径即为,求解即可.
【详解】把正四棱锥的侧面沿着SA剪开,得到它的侧面展开图(如图).
要使路程最短,必须沿着线段前行.
在中,,,则.
作于H,则,,.
故选:D.
4-3.(2024·辽宁·三模)盲盒是一种深受大众喜爱的玩具,某盲盒生产厂商要为棱长为的正四面体魔方设计一款正方体的包装盒,需要保证该魔方可以在包装盒内任意转动,则包装盒的棱长最短为( )
A.B.C.D.
【答案】B
【分析】依题意,若要使正四面体能自由转动,则正方体必须能装下正四面体的外接球,即正方体的最短棱长就是外接球的直径.
【详解】如图是棱长为的正四面体,
由题意, ,设的中点为,底面 的重心为,为外接球的球心,
则有 底面, , ,
,是外接球半径,
在 中, ,
在 中, ,,
,解得 ,
即正方体的最短棱长为.
故选:B.
4-4.(2024高一下·湖北武汉·期中)如图,一个矩形边长为1和4,绕它的长为的边旋转二周后所得如图的一开口容器(下表面密封),是中点,现有一只妈蚁位于外壁处,内壁处有一米粒,若这只蚂蚁要先爬到上口边沿再爬到点处取得米粒,则它所需经过的最短路程为( )
A.B.C.D.
【答案】A
【分析】画出圆柱的侧面展开图,根据对称性,求出的最小值就是的长,求解即可.
【详解】解:依题意可得圆柱的底面半径,高
将圆柱的侧面(一半)展开后得矩形,其中,,
问题转化为在上找一点,使最短,
作关于的对称点,连接,令与交于点,
则得的最小值就是为.
故选:A
4-5.(2024高一·全国·课后作业)如图所示,在正三棱柱中,,,由顶点沿棱柱侧面(经过棱)到达顶点,与的交点记为,则从点经点到的最短路线长为( )
A.B.C.4D.
【答案】B
【分析】沿侧棱将正三棱柱的侧面展开,根据展开图,即可得出最小路径.
【详解】如图,沿侧棱将正三棱柱的侧面展开
由侧面展开图可知,当,,三点共线时,从点经点到的路线最短.
所以最短路线长为.
故选:B.
(二)
基本立体图形的表面积的体积
1.(1)多面体的表面积是各个面的面积之和.
(2)旋转体的表面积是将其展开后,展开图的面积与底面面积之和.
(3)组合体的表面积求解时注意对衔接部分的处理.
2.空间几何体的体积的常用方法
公式法
规则几何体的体积,直接利用公式
割补法
把不规则的几何体分割成规则的几何体,或者把不规则的几何体补成规则的几何体
等体积法
通过选择合适的底面来求几何体体积的一种方法,特别是三棱锥的体积
题型5:基本立体图形的表面积
5-1.(2024·湖北武汉·模拟预测)已知某圆锥的母线长、底面圆的直径都等于球的半径,则球与圆锥的表面积之比为( )
A.8B.C.D.
【答案】B
【分析】根据球与圆锥的表面积计算公式,建立方程,可得答案.
【详解】设圆锥的母线长为,底面圆的半径为,球的半径为,则,即,,
球的表面积,圆锥的表面积,
则.
故选:B.
5-2.(2024·河南郑州·模拟预测)在一个正六棱柱中挖去一个圆柱后,剩余部分几何体如图所示.已知正六棱柱的底面正六边形边长为3cm,高为4cm,内孔半径为1cm,则此几何体的表面积是( ).
A.B.
C.D.
【答案】C
【分析】根据棱柱与圆柱的侧面积公式求解.
【详解】所求几何体的侧面积为,
上下底面面积为,
挖去圆柱的侧面积为,
则所求几何体的表面积为.
故选:C.
5-3.(2024·安徽安庆·三模)陀螺起源于我国,最早出土的石制陀螺是在山西夏县发现的新石器时代遗址.如图所示的是一个陀螺立体结构图.已知,底面圆的直径,圆柱体部分的高,圆锥体部分的高,则这个陀螺的表面积(单位:)是( )
A.B.
C.D.
【答案】C
【分析】
根据圆柱与圆锥的表面积公式求解.
【详解】由题意可得圆锥体的母线长为,
所以圆锥体的侧面积为,
圆柱体的侧面积为,
圆柱的底面面积为,
所以此陀螺的表面积为,
故选:C.
5-4.(2024·河北·模拟预测)《九章算术》是我国古代的数学名著.其“商功”中记载:“正四面形棱台(即正四棱台)建筑物为方亭.”现有如图所示的烽火台,其主体部分为一方亭,将它的主体部分抽象成的正四棱台(如图所示),其中上底面与下底面的面积之比为,方亭的高为棱台上底面边长的倍.已知方亭的体积为,则该方亭的表面积约为( )(,,)
A.B.C.D.
【答案】C
【分析】设方亭相应的正四棱台的上底面边长,则,棱台的高,根据棱台的体积求出,再根据棱台的表面积公式计算可得.
【详解】设方亭相应的正四棱台的上底面边长,则,棱台的高,
所以,解得,
所以正四棱台的上底面边长为,下底面边长为,棱台的高为,
所以方亭的斜高为,
由于各侧面均为相等的等腰梯形,所以,
所以方亭的表面积.
故选:C
5-5.(2024高三下·海南海口·期中)如图是一个圆台形的水杯,圆台的母线长为12,上、下底面的半径分别为4和2.为了防烫和防滑,该水杯配有一个皮革杯套,包裹住水杯高度以下的外壁和杯底,水杯和杯套的厚度忽略不计,则此杯套使用的皮革的面积为( )
A.B.C.D.
【答案】C
【分析】求出杯套部分圆台的较大底面的半径,根据圆台的侧面积公式以及底面圆的面积,即可求得答案.
【详解】由题意可知杯套部分依然是圆台,则此杯套使用的皮革的面积即为对应圆台的侧面积加上较小底面面积;
如图,作出水杯的轴截面,作于G,
设为杯套部分对应的轴截面,AG交EF与H,
则,,
则由∽可得,
故,
故此杯套使用的皮革的面积为,
故选:C
题型6:基本立体图形的体积
6-1.(2024高三上·重庆沙坪坝·阶段练习)若某圆锥的侧面展开图是一个半径为2的半圆面,其内接正四棱柱的高为,则此正四棱柱的体积是( )
A.B.C.D.
【答案】C
【分析】求出圆锥的底面半径与高,设棱柱的底面对角线长的一半为,高为h,根据比例式得出,h的关系,可求的值,根据柱体的体积公式可得答案.
【详解】设圆锥底面半径为,因为母线长为,
则半圆弧长底面周长,
所以,圆锥的高为
如图,设,则,设,则,
因为,
∴,
所以,
∴,,
故选:C.
6-2.(2024高三上·山东青岛·期中)已知正四棱锥的各顶点都在同一个球面上,球的体积为,则该正四棱锥的体积最大值为( )
A.18B.C.D.27
【答案】B
【分析】先求出外接球的半径,再根据正四棱锥的几何特征可知外接球的球心在其高上,利用勾股定理可得,进而由体积公式转化为关于的函数,利用导数可求出函数的最值.
【详解】如图,设正四棱锥的底面边长,高,外接球的球心为,则,
因为球的体积为,所以球的半径为,
在中,,即,
所以正四棱锥的体积为
整理得,则,
当时,,当时,,
所以在上递增,在上递减,
所以当时,函数取得最大值,
故选:B
6-3.(2024高三上·湖北武汉·开学考试)攒尖是我国古代建筑中屋顶的一种结构形式,宋代称为最尖,清代称攒尖,通常有圆形攒尖、三角攒尖、四角攒尖、八角攒尖,也有单檐和重檐之分,多见于亭阁式建筑、园林建筑.下面以四角攒尖为例,如图,它的屋顶部分的轮廓可近似看作一个正四棱锥.已知正四棱锥的底面边长为米,侧棱长为5米,则其体积为( )立方米.
A.B.24C.D.72
【答案】B
【分析】作图,根据正四棱锥的性质求解高即可得体积.
【详解】如图所示,在正四棱锥中,连接于,则为正方形的中心,
连接,则底面边长,对角线,.
又,故高.
故该正四棱锥体积为.
故选:B
6-4.(2024·浙江·模拟预测)如图是我国古代量粮食的器具“升”,其形状是正四棱台,上、下底面边长分别为20cm和10cm,侧棱长为cm.“升”装满后用手指或筷子沿升口刮平,这叫“平升”.则该“升”的“平升”约可装( )
A.1.5LB.1.7LC.2.3LD.2.7L
【答案】C
【分析】根据棱台的体积公式求解即可.
【详解】根据题意画出正四棱台的直观图,其中底面是边长为20的正方形,底面是边长为10的正方形,侧棱,记底面和底面的中心分别为和,则是正四棱台的高.
过作平面的垂线,垂足为,则且,,
所以,,
故,
所以棱台的高,
由棱台的体积公式得.
故选:C .
6-5.(2024高三上·广西·阶段练习)在棱长为2的正方体内,放入一个以为铀线的圆柱,且圆柱的底面所在平面截正方体所得的截面为三角形,则该圆柱体积的最大值为 .
【答案】
【分析】易得圆柱的底面所在平面截正方体所得的截面为正三角形,该正三角形的内切圆即为圆柱的底面,根据为铀线,求出圆柱的高,表示出圆柱的体积,利用导数求出最大值.
【详解】如图,连接,,,,
因为平面,平面,则,
又,平面,平面,,
平面,故,同理可得,
平面,平面,,平面,
设圆柱的一个底面所在平面截正方体所得的截面为,则为正三角形,
由圆柱可知轴线平面,又平面,所以平面平面,
设(),则,
所以内切圆的半径,
点到平面的距离.
因为,所以圆柱的高,
圆柱的体积,
,则在上单调递增,
所以.
故答案为:
相关试卷
这是一份备战2025年高考数学一轮专题复习全套考点突破和专题检测专题26数列的概念6题型分类(原卷版+解析),共60页。试卷主要包含了数列的有关概念等内容,欢迎下载使用。
这是一份备战2025年高考数学一轮专题复习全套考点突破和专题检测专题08函数的图象6题型分类(原卷版+解析),共122页。试卷主要包含了掌握基本初等函数的图像,函数图像作法,填空题,解答题等内容,欢迎下载使用。
这是一份专题30 数列求和5题型分类-备战2025年高考数学一轮专题复习全套考点突破和专题检测(解析版),共94页。试卷主要包含了公式法,分组求和法与并项求和法,错位相减法,裂项相消法等内容,欢迎下载使用。








