备战2025年高考数学一轮专题复习全套考点突破和专题检测专题35空间向量的概念与运算5题型分类(原卷版+解析)

这是一份备战2025年高考数学一轮专题复习全套考点突破和专题检测专题35空间向量的概念与运算5题型分类(原卷版+解析)，共118页。试卷主要包含了空间向量的有关概念，空间向量的数量积及运算律，四点共面，个.等内容，欢迎下载使用。

1．空间向量的有关概念
2.空间向量的有关定理
(1)共线向量定理：对任意两个空间向量a，b(b≠0)，a∥b的充要条件是存在实数λ，使a＝λb.
(2)共面向量定理：如果两个向量a，b不共线，那么向量p与向量a，b共面的充要条件是存在唯一的有序实数对(x，y)，使p＝xa＋yb.
(3)空间向量基本定理
如果三个向量a，b，c不共面，那么对任意一个空间向量p，存在唯一的有序实数组(x，y，z)，使得p＝xa＋yb＋zc，{a，b，c}叫做空间的一个基底．
3．空间向量的数量积及运算律
(1)数量积
非零向量a，b的数量积a·b＝|a||b|cs〈a，b〉．
(2)空间向量的坐标表示及其应用
设a＝(a1，a2，a3)，b＝(b1，b2，b3)．
4.空间位置关系的向量表示
(1)直线的方向向量：如果表示非零向量a的有向线段所在直线与直线l平行或重合，则称此向量a为直线l的方向向量．
(2)平面的法向量：直线l⊥α，取直线l的方向向量a，则向量a为平面α的法向量．
(3)空间位置关系的向量表示
常用结论
1．三点共线：在平面中A，B，C三点共线⇔eq \(OA,\s\up6(→))＝xeq \(OB,\s\up6(→))＋yeq \(OC,\s\up6(→))(其中x＋y＝1)，O为平面内任意一点．
2．四点共面：在空间中P，A，B，C四点共面⇔eq \(OP,\s\up6(→))＝xeq \(OA,\s\up6(→))＋yeq \(OB,\s\up6(→))＋zeq \(OC,\s\up6(→))(其中x＋y＋z＝1)，O为空间中任意一点．
一、单选题
1．（2024高二下·江苏泰州·期中）若点，，在同一条直线上，则（ ）
A．21B．4C．4D．10
2．（2024高二上·山东菏泽·阶段练习）对于空间任意一点和不共线的三点，有如下关系：，则（ ）
A．四点必共面B．四点必共面
C．四点必共面D．五点必共面
3．（2024高二上·陕西商洛·阶段练习）已知，则下列向量中与平行的是（ ）
A．B．C．D．
4．（2024高二上·北京西城·期中）两个不同的平面和，平面的一个法向量为，平面的一个法向量，则平面与平面（ ）
A．平行B．垂直C．相交D．不能确定
5．（2024高二·全国·课后作业）下面关于空间向量的说法正确的是（ ）
A．若向量平行，则所在直线平行
B．若向量所在直线是异面直线，则不共面
C．若A，B，C，D四点不共面，则向量，不共面
D．若A，B，C，D四点不共面，则向量，，不共面
6．（2024高二上·安徽阜阳·阶段练习）下列命题中是假命题的是（ ）
A．任意向量与它的相反向量不相等
B．和平面向量类似，任意两个空间向量都不能比较大小
C．如果，则
D．两个相等的向量，若起点相同，则终点也相同
7．（2024高二上·浙江台州·阶段练习）已知平面的法向量为，，则直线和平面的位置关系是（ ）
A．B．C．与相交但不垂直D．
8．（2024高二上·全国·课后作业）若空间中任意四点O，A，B，P满足，其中m＋n＝1，则（ ）
A．P∈ABB．P∉AB
C．点P可能在直线AB上D．以上都不对
9．（2024高二上·全国·课后作业）已知在空间单位正交基底下，是空间的一组单位正交基底，是空间的另一组基底.若向量在基底下的坐标为，则向量在基底下的坐标为（ ）
A．B．C．D．
10．（2024高二上·新疆和田·期中）已知、分别为不重合的两直线、的方向向量，、分别为不重合的两平面、的法向量，则下列所有正确结论（ ）个.
①；②；③；④.
A．B．C．D．
11．（2024·福建福州·三模）以下四组向量在同一平面的是（ ）
A．、、B．、、
C．、、D．、、
12．（2024高二上·云南昆明·期末）如图，M在四面体OABC的棱BC的中点，点N在线段OM上，且，设，，，则下列向量与相等的向量是（ ）
A．B．
C．D．
13．（2024高三上·广东广州·阶段练习）如图所示的木质正四棱锥模型，过点A作一个平面分别交于点E，F，G，若，则的值为（ ）
A．B．C．D．
14．（2024·江西·二模）在四棱锥中，棱长为2的侧棱垂直底面边长为2的正方形，为棱的中点，过直线的平面分别与侧棱、相交于点、，当时，截面的面积为（ ）
A．B．2C．D．3
二、多选题
15．（2024高二下·浙江·期中）空间直角坐标系中，已知，，，，则（ ）
A．
B．是等腰直角三角形
C．与平行的单位向量的坐标为或
D．在方向上的投影向量的坐标为
16．（2024·广东佛山·二模）四面体中，，，，，，平面与平面的夹角为，则的值可能为（ ）
A．B．C．D．
三、填空题
17．（2024·上海金山·二模）已知向量，向量，则与的夹角的大小为 .
18．（2024高二上·北京西城·期中）已知平面的法向量为，平面的法向量为，若，则 ．
19．（2024高二上·山西·开学考试）已知直线的方向向量是，平面的法向量是，与的位置关系为 .
20．（2024高二下·天津蓟州·期中）已知点A（1，2，3），B（0，1，2），C（﹣1，0，λ），若A，B，C三点共线，则 ．
21．（2024高二上·湖南株洲·阶段练习）已知向量，若，则 ．
22．（2024高二上·北京·期中）直线的方向向量为，直线的方向向量为，平面的法向量为，，，则、、的值依次为 .
23．（2024高二上·浙江台州·阶段练习）如图，三棱锥中，平面ABC，，且，．若D是棱PC上的点，满足，且，则 ．
24．（2024高二上·江西宜春·阶段练习）如图所示，在正方体中，E是棱DD1的三等分点（靠近点），点F在棱C1D1上，且，若∥平面，则 .
四、解答题
25．（2024高三·全国·专题练习）如图，在四棱锥中，底面，底面是矩形，，分别是的中点，.证明：.
26．（2024高二下·江苏·课后作业）在正方体中，分别是的中点，试建立适当的空间直角坐标系，求证：平面平面.
27．（2024高一·全国·专题练习）如图所示，正四棱的底面边长1，侧棱长4，中点为，中点为．求证：平面平面.

28．（2024高三·全国·对口高考）如图所示的几何体中，四边形是等腰梯形，，，平面，，.

(1)求二面角的余弦值；
(2)在线段AB（含端点）上，是否存在一点P，使得平面.若存在，求出的值；若不存在，请说明理由.
29．（2024高一·全国·专题练习）如图，且，，且，且，平面ABCD，.若M为CF的中点，N为EG的中点，求证：平面CDE；
30．（2024高二上·广东广州·阶段练习）如图，在正方体中，E，F分别是，的中点．
(1)求证：；
(2)求证：平面
31．（2024高二下·江苏·课后作业）已知棱长为1的正方体在空间直角坐标系中的位置如图所示，分别为棱的中点，求证：.
32．（2024高二·全国·专题练习）如图所示，平面平面，四边形为正方形，是直角三角形，且，，，分别是线段，，的中点，求证：平面平面．
33．（2024高三·全国·专题练习）如图，在几何体ABCDE中，ABC，BCD，CDE均为边长为2的等边三角形，平面ABC⊥平面BCD，平面DCE⊥平面BCD．求证：A，B，D，E四点共面；
34．（2024高三·全国·专题练习）如图，直三棱柱中，，，，D为BC的中点，E为上的点，且．求证：平面；
35．（2024高三·全国·专题练习）如图，直三棱柱的侧面为正方形，，E，F分别为，的中点，．证明：平面；
36．（2024高三·全国·专题练习）在正方体中，如图、分别是，的中点．求证：平面平面；
37．（2024高二·全国·专题练习）如图，正三棱柱中，分别是棱上的点，.

证明：平面平面.
38．（2024高三·全国·专题练习）已知直三棱柱中，侧面为正方形，，E，F分别为AC和的中点，D为棱上的动点..证明：；
39．（2024高三·全国·专题练习）如图，在四棱锥中，底面ABCD是菱形，，，，底面ABCD，，点E在棱PD上，且.证明：平面平面ACE；
40．（2024高三·全国·专题练习）如图，在三棱柱中，平面ABC，，，D为的中点，交于点E．证明：.
41．（2024高三·全国·专题练习）如图，在底面是矩形的四棱锥中，平面，，，是PD的中点.
求证：平面平面.
42．（2024高三·全国·专题练习）如图，棱台中，，底面ABCD是边长为4的正方形，底面是边长为2的正方形，连接，BD，.证明：.
43．（2024·云南曲靖·模拟预测）如图，已知四棱锥的底面是平行四边形，侧面是等边三角形，.
(1)求证：平面平面；
(2)设为侧棱上一点，四边形是过两点的截面，且平面，是否存在点，使得平面平面？若存在，求的值；若不存在，说明理由.
44．（2024高三·全国·专题练习）斜三棱柱的各棱长都为，点在下底面的投影为的中点.在棱（含端点）上是否存在一点使？若存在，求出的长；若不存在，请说明理由；
45．（2024高三·全国·专题练习）斜三棱柱的各棱长都为2，，点在下底面ABC的投影为AB的中点O．在棱（含端点）上是否存在一点D使？若存在，求出BD的长；若不存在，请说明理由；
46．（2024·河北保定·一模）如图，平行六面体的所有棱长均为，底面为正方形，，点为的中点，点为的中点，动点在平面内．
(1)若为中点，求证：；
(2)若平面，求线段长度的最小值．
47．（2024高二上·北京海淀·期中）已知三棱锥（如图1）的平面展开图（如图2）中，四边形为边长为的正方形，和均为正三角形.在三棱锥中：
(1)求点到平面的距离；
(2)若点在棱上，满足，点在棱上，且，求的取值范围.
48．（2024高三·全国·专题练习）如图，在四棱锥中，底面ABCD为正方形，平面ABCD，E为PD的中点，.求证：PB平面AEC；
49．（2024高二上·山东聊城·阶段练习）如图，正方形与梯形所在平面互相垂直，已知，，．

(1)求证：平面．
(2)线段上是否存在点M，使平面平面？若存在，求出的值；若不存在，请说明理由．
50．（2024高二·阶段练习）如图，在四棱锥中，平面，，，，点为棱的中点．证明：

(1)平面；
(2)平面⊥平面．
51．（2024高三·全国·专题练习）在苏州博物馆有一类典型建筑八角亭，既美观又利于采光，其中一角如图所示，为多面体，，，，底面，四边形是边长为2的正方形且平行于底面，，，的中点分别为，，，．证明：//平面；

52．（2024高二上·广东佛山·阶段练习）如图，在正方体中，分别是的中点

(1)证明：平面.
(2)在直线上是否存在点，使得平面？若存在，请指出的位置；若不存在.请说明理由.
53．（2024高三·全国·专题练习）在四棱锥中，平面ABCD⊥平面PCD，底面ABCD为梯形．，，且，，．若M是棱PA的中点，则对于棱BC上是否存在一点F，使得MF与PC平行．

54．（2024高二上·山西大同·期中）如图，在直三棱柱中，，垂足为，为线段上的一点.

(1)若为线段的中点，证明：平面；
(2)若平面平面，求的值.
55．（2024高二下·江苏·课后作业）如图，四边形ABCD和ABEF都是平行四边形，且不共面，M，N分别是AC，BF的中点，求证：.
56．（2024高二·全国·课后作业）如图，在平行六面体中，，．
(1)求证：、、三点共线；
(2)若点是平行四边形的中心，求证：、、三点共线．
57．（2024高二上·湖北宜昌·期中）如图，在棱长为2的正方体中，点分别是线段的中点.

(1)求证：
(2)求三棱锥的体积.
58．（2024高三·全国·专题练习）如图四棱锥，且，平面平面，且是以为直角的等腰直角三角形，其中为棱的中点，点在棱上，且.求证：四点共面.
59．（2024高二上·河北邢台·阶段练习）如图，在边长为3的正方体中，点P，Q，R分别在棱，，上，且.
（1）求点D到平面的距离；
（2）若平面与线段的交点为N，求的值.
60．（2024高三·全国·专题练习）已知E，F，G，H分别是空间四边形ABCD的边AB，BC，CD，DA的中点，用向量法证明：
(1)E，F，G，H四点共面；
(2)平面EFGH．
61．（2024·四川泸州·模拟预测）如图，四边形为正方形，若平面平面，，，.
(1)求二面角A－CF－D的余弦值；
(2)判断点D与平面CEF的位置关系，并说明理由.
62．（2024·河南郑州·一模）如图，正四棱锥的底面边长和高均为2，，分别为，的中点．
(1)若点是线段上的点，且，判断点是否在平面内，并证明你的结论；
(2)求直线与平面所成角的正弦值．
63．（2024·江苏·三模）如图，三棱锥P－ABC的底面为等腰直角三角形，∠ABC＝90°，AB＝2．D，E分别为AC，BC的中点，PD⊥平面ABC，点M在线段PE上．
(1)再从条件①、②、③、④四个条件中选择两个作为已知，使得平面MBD⊥平面PBC，并给予证明；
(2)在（1）的条件下，求直线BP与平面MBD所成的角的正弦值．
条件①：；
条件②：∠PED＝60°；
条件③：PM＝3ME：
条件④：PE＝3ME
成套的课件成套的教案成套的试题成套的微专题尽在高中数学同步资源大全QQ群552511468也可联系微信fjshuxue加入百度网盘群1.5T一线老师必备资料一键转存自动更新永不过期
名称
定义
空间向量
在空间中，具有大小和方向的量
相等向量
方向相同且模相等的向量
相反向量
长度相等而方向相反的向量
共线向量(或平行向量)
表示若干空间向量的有向线段所在的直线互相平行或重合的向量
共面向量
平行于同一个平面的向量
向量表示
坐标表示
数量积
a·b
a1b1＋a2b2＋a3b3
共线
a＝λb(b≠0，λ∈R)
a1＝λb1，a2＝λb2，a3＝λb3
垂直
a·b＝0(a≠0，b≠0)
a1b1＋a2b2＋a3b3＝0
模
|a|
eq \r(a\\al(2,1)＋a\\al(2,2)＋a\\al(2,3))
夹角余弦值
cs〈a，b〉＝eq \f(a·b,|a||b|)(a≠0，b≠0)
cs〈a，b〉＝eq \f(a1b1＋a2b2＋a3b3,\r(a\\al(2,1)＋a\\al(2,2)＋a\\al(2,3))·\r(b\\al(2,1)＋b\\al(2,2)＋b\\al(2,3)))
位置关系
向量表示
直线l1，l2的方向向量分别为n1，n2
l1∥l2
n1∥n2⇔n1＝λn2(λ∈R)
l1⊥l2
n1⊥n2⇔n1·n2＝0
直线l的方向向量为n，平面α的法向量为m，l⊄α
l∥α
n⊥m⇔n·m＝0
l⊥α
n∥m⇔n＝λm(λ∈R)
平面α，β的法向量分别为n，m
α∥β
n∥m⇔n＝λm(λ∈R)
α⊥β
n⊥m⇔n·m＝0
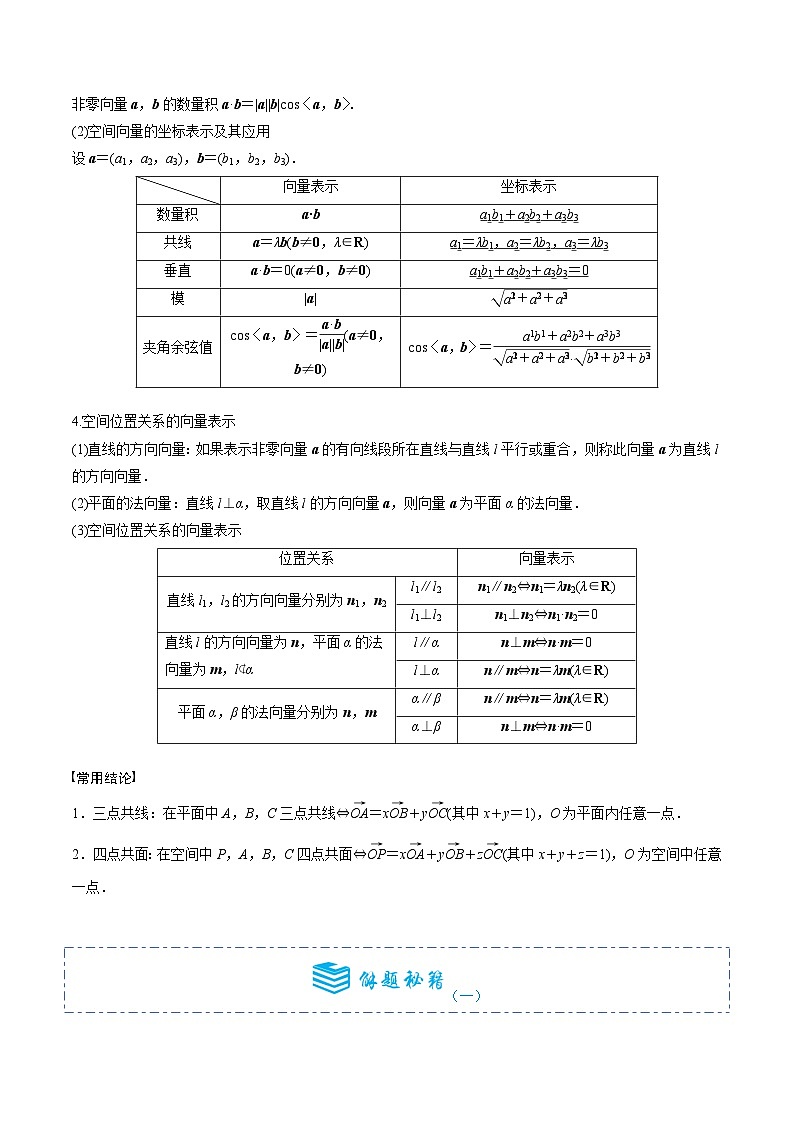
（一）
用已知向量表示某一向量的三个关键点
(1)要结合图形，以图形为指导是解题的关键．
(2)要正确理解向量加法、减法与数乘运算的几何意义．
(3)在立体几何中，三角形法则、平行四边形法则仍然成立．
题型1：空间向量的线性运算
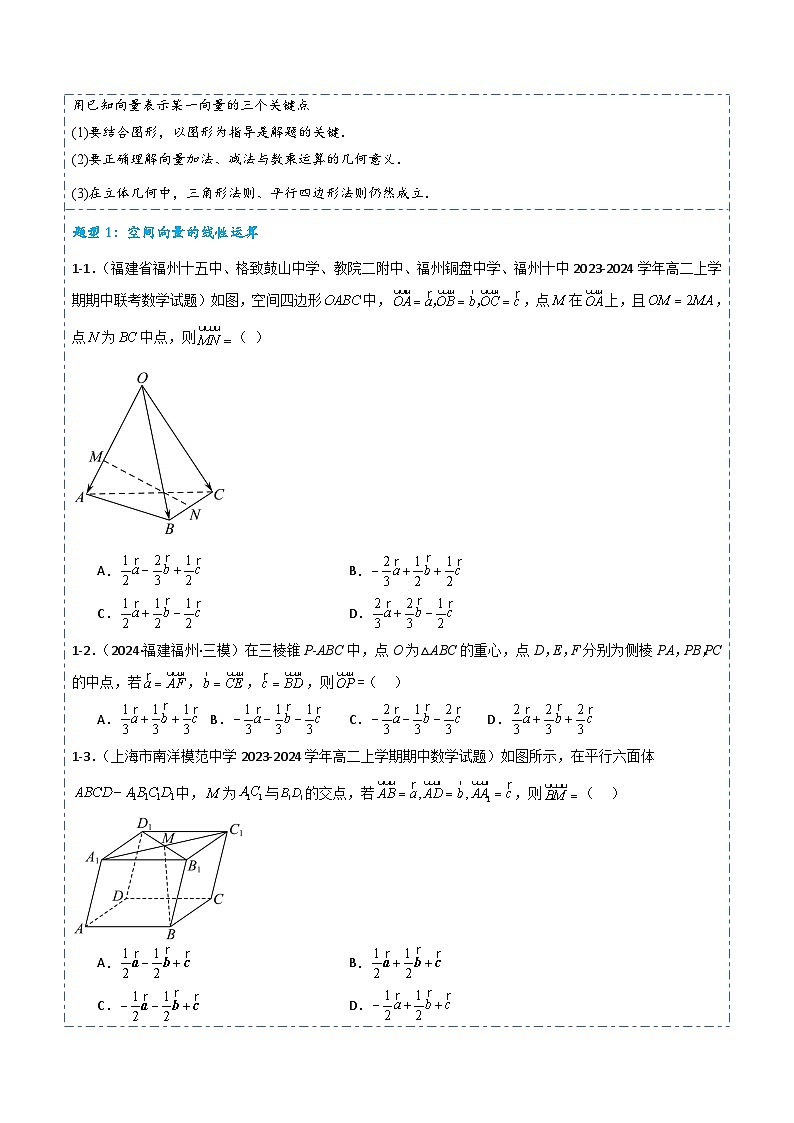
1-1．（福建省福州十五中、格致鼓山中学、教院二附中、福州铜盘中学、福州十中2023-2024学年高二上学期期中联考数学试题）如图，空间四边形中，，点在上，且，点为中点，则（ ）
A．B．
C．D．
1-2．（2024·福建福州·三模）在三棱锥P-ABC中，点O为△ABC的重心，点D，E，F分别为侧棱PA，PB，PC的中点，若，，，则=（ ）
A．B．C．D．
1-3．（上海市南洋模范中学2023-2024学年高二上学期期中数学试题）如图所示，在平行六面体中，为与的交点，若，则（ ）

A．B．
C．D．
1-4．（2024高二上·陕西西安·期末）如图，在四面体中，是的重心，是上的一点，且，若，则为（ ）
A．B．
C．D．
（二）
应用共线(面)向量定理、证明点共线(面)的方法比较
三点(P，A，B)共线
空间四点(M，P，A，B)共面
eq \(PA,\s\up6(→))＝λeq \(PB,\s\up6(→))
eq \(MP,\s\up6(→))＝xeq \(MA,\s\up6(→))＋yeq \(MB,\s\up6(→))
对空间任一点O，eq \(OP,\s\up6(→))＝eq \(OA,\s\up6(→))＋teq \(AB,\s\up6(→))
对空间任一点O，eq \(OP,\s\up6(→))＝eq \(OM,\s\up6(→))＋xeq \(MA,\s\up6(→))＋yeq \(MB,\s\up6(→))
对空间任一点O，eq \(OP,\s\up6(→))＝xeq \(OA,\s\up6(→))＋(1－x)eq \(OB,\s\up6(→))
对空间任一点O，eq \(OP,\s\up6(→))＝xeq \(OM,\s\up6(→))＋yeq \(OA,\s\up6(→))＋(1－x－y)eq \(OB,\s\up6(→))
题型2：空间向量基本定理及其应用
2-1．（2024高二上·湖南郴州·阶段练习）已知，，如果与为共线向量，则（ ）
A．B．C．D．
2-2．（2024高二·全国·课后作业）若、、三点共线，则（ ）．
A．
B．
C．
D．
2-3．（湖南省岳阳市平江县2023-2024学年高二上学期1月期末数学试题）已知A、B、C三点不共线，对平面外的任一点O，下列条件中能确定点M与点A、B、C一定共面的是（ ）
A．B．
C．D．
2-4．（2024高二下·四川雅安·期末）向量，分别是直线，的方向向量，且，，若，则（ ）
A．，B．，
C．，D．，
2-5．（2024高二下·江苏扬州·期中）已知空间、、、四点共面，且其中任意三点均不共线，设为空间中任意一点，若，则（ ）
A．B．C．D．
2-6．（2024高二上·湖南郴州·阶段练习）为空间任意一点，若，若、、、四点共面，则（ ）
A．B．C．D．
2-7．（2024高三·全国·专题练习）已知，若三向量共面，则等于（ ）
A．B．9C．D．
2-8．（2024高二·全国·课后作业）在四面体OABC中，点M，N分别为OA、BC的中点，若，且G、M、N三点共线，则 ．
（三）
空间向量数量积及其应用
空间向量的数量积运算有两条途径，一是根据数量积的定义，利用模与夹角直接计算；二是利用坐标运算．
题型3：空间向量数量积及其应用
3-1．【多选】（2024高二上·辽宁大连·期末）已知向量，，则下列正确的是（ ）
A．B．C．D．
3-2．（2024高二上·山东济宁·阶段练习）已知是棱长为2的正方体内切球的一条直径，则 ．
3-3．（2024·上海松江·二模）已知空间向量，，，若，则 ．
3-4．（2024高二上·重庆万州·阶段练习）已知空间向量，，则在方向上的投影向量为 .
3-5．（2024·黑龙江哈尔滨·模拟预测）如图，平行六面体中，，，，，则线段的长为 .

3-6．【多选】（2024高三上·黑龙江哈尔滨·期中）如图，在平行六面体中，其中以顶点A为端点的三条棱长均为6，且彼此夹角都是，下列说法中不正确的是（ ）

A．
B．
C．向量与夹角是
D．向量与所成角的余弦值为
3-7．【多选】（2024高二上·浙江温州·期末）已知空间向量，，下列说法正确的是（ ）
A．若，则
B．若，则
C．若在上的投影向量为，则
D．若与夹角为锐角，则
3-8．【多选】（2024·安徽·一模）在平行六面体中，已知，，则（ ）
A．直线与所成的角为
B．线段的长度为
C．直线与所成的角为
D．直线与平面所成角的正弦值为
（四）
向量法证明平行、垂直
(1)利用向量法证明平行、垂直关系，关键是建立恰当的坐标系(尽可能利用垂直条件，准确写出相关点的坐标，进而用向量表示涉及到直线、平面的要素)．
(2)向量证明的核心是利用向量的数量积或数乘向量，但向量证明仍然离不开立体几何的有关定理．
题型4：向量法证明平行
4-1．（2024高三·全国·专题练习）四棱锥中，底面为矩形，平面，为的中点，证明：平面.
4-2．（2024高二下·江苏·课后作业）如图所示，平面PAD⊥平面ABCD，四边形ABCD为正方形，△PAD是直角三角形，且PA＝AD＝2，E，F，G分别是线段PA，PD，CD的中点，求证：平面EFG∥平面PBC．
4-3．（2024高二·全国·课后作业）如图，在直四棱柱中，底面为等腰梯形，，，，，是棱的中点．求证：平面平面.
4-4．（2024高二·全国·专题练习）如图，在四棱锥中，底面为矩形，平面平面，，，，，分别是，的中点. 求证：平面.

4-5．（2024高二上·全国·课后作业）如图所示，在四棱锥中，底面为矩形，平面，为的中点，为的中点，，求证：．

题型5：向量法证明垂直
5-1．（2024高三·全国·专题练习）如图，在四棱锥中，平面，，，，.为的中点，点在上，且.
求证：平面平面.
5-2．（2024高二·全国·专题练习）已知在直三棱柱中，其中为的中点，点是上靠近的四等分点，与底面所成角的余弦值为．

求证：平面平面.
5-3．（2024高三·全国·专题练习）如图，已知直三棱柱为的中点，为侧棱上一点，且，三棱柱的体积为32．过点作，垂足为点，求证：平面；
5-4．（2024高三·全国·专题练习）如图，在四棱锥中，底面，底面是边长为2的正方形，，，分别是，的中点．求证：平面；
5-5．（2024高二上·山西太原·期中）如图，在平行六面体中，.
(1)求的长；
(2)求证：.
专题35 空间向量的概念与运算5题型分类
1．空间向量的有关概念
2.空间向量的有关定理
(1)共线向量定理：对任意两个空间向量a，b(b≠0)，a∥b的充要条件是存在实数λ，使a＝λb.
(2)共面向量定理：如果两个向量a，b不共线，那么向量p与向量a，b共面的充要条件是存在唯一的有序实数对(x，y)，使p＝xa＋yb.
(3)空间向量基本定理
如果三个向量a，b，c不共面，那么对任意一个空间向量p，存在唯一的有序实数组(x，y，z)，使得p＝xa＋yb＋zc，{a，b，c}叫做空间的一个基底．
3．空间向量的数量积及运算律
(1)数量积
非零向量a，b的数量积a·b＝|a||b|cs〈a，b〉．
(2)空间向量的坐标表示及其应用
设a＝(a1，a2，a3)，b＝(b1，b2，b3)．
4.空间位置关系的向量表示
(1)直线的方向向量：如果表示非零向量a的有向线段所在直线与直线l平行或重合，则称此向量a为直线l的方向向量．
(2)平面的法向量：直线l⊥α，取直线l的方向向量a，则向量a为平面α的法向量．
(3)空间位置关系的向量表示
常用结论
1．三点共线：在平面中A，B，C三点共线⇔eq \(OA,\s\up6(→))＝xeq \(OB,\s\up6(→))＋yeq \(OC,\s\up6(→))(其中x＋y＝1)，O为平面内任意一点．
2．四点共面：在空间中P，A，B，C四点共面⇔eq \(OP,\s\up6(→))＝xeq \(OA,\s\up6(→))＋yeq \(OB,\s\up6(→))＋zeq \(OC,\s\up6(→))(其中x＋y＋z＝1)，O为空间中任意一点．
一、单选题
1．（2024高二下·江苏泰州·期中）若点，，在同一条直线上，则（ ）
A．21B．4C．4D．10
【答案】C
【分析】若∥，则．
【详解】，
∵点，，在同一条直线上
∴∥则
解得
∴
故选：C．
2．（2024高二上·山东菏泽·阶段练习）对于空间任意一点和不共线的三点，有如下关系：，则（ ）
A．四点必共面B．四点必共面
C．四点必共面D．五点必共面
【答案】B
【分析】根据如下结论判断：对于空间任一点和不共线三点，若点满足且，则四点共面.
【详解】对于空间任一点和不共线三点，若点满足且，则四点共面.
而，其中，所以四点共面.
故选：B.
3．（2024高二上·陕西商洛·阶段练习）已知，则下列向量中与平行的是（ ）
A．B．C．D．
【答案】B
【分析】利用共线向量基本定理，判断即可.
【详解】因为，所以与平行.
故选：B.
【点睛】本题考查了空间向量共线的判断，属于基础题.
4．（2024高二上·北京西城·期中）两个不同的平面和，平面的一个法向量为，平面的一个法向量，则平面与平面（ ）
A．平行B．垂直C．相交D．不能确定
【答案】A
【分析】根据的坐标，判断二者共线，即可判断平面与平面的位置关系.
【详解】由题意知，，
则，即共线，则，
故选：A
5．（2024高二·全国·课后作业）下面关于空间向量的说法正确的是（ ）
A．若向量平行，则所在直线平行
B．若向量所在直线是异面直线，则不共面
C．若A，B，C，D四点不共面，则向量，不共面
D．若A，B，C，D四点不共面，则向量，，不共面
【答案】D
【分析】
利用平行向量的意义判断A；利用空间共面向量的意义判断BCD作答.
【详解】
向量平行，所在直线可以重合，也可以平行，A错误；
可以通过平移将空间中任意两个向量平移到一个平面内，因此空间任意两个向量都是共面的，BC错误；
显然AB，AC，AD是空间中有公共端点A，但不共面的三条线段，所以向量，，不共面，D正确.
故选：D
6．（2024高二上·安徽阜阳·阶段练习）下列命题中是假命题的是（ ）
A．任意向量与它的相反向量不相等
B．和平面向量类似，任意两个空间向量都不能比较大小
C．如果，则
D．两个相等的向量，若起点相同，则终点也相同
【答案】A
【分析】由零向量的定义可判断AC，由向量的性质可判断BD.
【详解】对于A，零向量的相反向量是它本身，A错误；
对于B，空间向量是有向线段，不能比较大小，B正确；
对于C，如果，则，C正确；
对于D，两个相等的向量，若起点相同，则终点也相同，D正确.
故选：A.
7．（2024高二上·浙江台州·阶段练习）已知平面的法向量为，，则直线和平面的位置关系是（ ）
A．B．C．与相交但不垂直D．
【答案】D
【分析】利用空间向量判定线面关系即可.
【详解】由题意可知，即.
故选：D
8．（2024高二上·全国·课后作业）若空间中任意四点O，A，B，P满足，其中m＋n＝1，则（ ）
A．P∈ABB．P∉AB
C．点P可能在直线AB上D．以上都不对
【答案】A
【分析】由已知化简可得，即可判断.
【详解】因为m＋n＝1，所以m＝1－n，
所以，即，
即，所以与共线．
又，有公共起点A，
所以P，A，B三点在同一直线上，即P∈AB.
故选：A.
9．（2024高二上·全国·课后作业）已知在空间单位正交基底下，是空间的一组单位正交基底，是空间的另一组基底.若向量在基底下的坐标为，则向量在基底下的坐标为（ ）
A．B．C．D．
【答案】C
【分析】利用空间向量基本定理求解即可.
【详解】设向量在基底下的坐标为，则，
又向量在基底下的坐标为，则，
所以，即，
所以解得
所以向量在基底下的坐标为.
故选：C.
10．（2024高二上·新疆和田·期中）已知、分别为不重合的两直线、的方向向量，、分别为不重合的两平面、的法向量，则下列所有正确结论（ ）个.
①；②；③；④.
A．B．C．D．
【答案】D
【详解】根据直线的方向向量与平面向量的法向量的定义判断即可.
【分析】因为、分别为不重合的两直线、的方向向量，、分别为不重合的两平面、的法向量；
直线，的方向向量平行（垂直）等价于直线、平行（垂直），故①、②正确；
平面，的法向量平行（垂直）等价于平面，平行（垂直）、故③、④正确；
故选：D.
11．（2024·福建福州·三模）以下四组向量在同一平面的是（ ）
A．、、B．、、
C．、、D．、、
【答案】B
【分析】利用共面向量的基本定理逐项判断可得出合适的选项.
【详解】对于A选项，设，所以，，无解；
对于B选项，因为，故B选项中的三个向量共面；
对于C选项，设，所以，，无解；
对于D选项，设，所以，，矛盾.
故选：B.
12．（2024高二上·云南昆明·期末）如图，M在四面体OABC的棱BC的中点，点N在线段OM上，且，设，，，则下列向量与相等的向量是（ ）
A．B．
C．D．
【答案】A
【分析】由题意得出，再用向量线性运算化简后可得.
【详解】因为M在四面体OABC的棱BC的中点，所以，
又点N在线段OM上，且，
故点为的三等分点，所以，
所以.
故选与相等的向量的向量是；
故选：A.
13．（2024高三上·广东广州·阶段练习）如图所示的木质正四棱锥模型，过点A作一个平面分别交于点E，F，G，若，则的值为（ ）
A．B．C．D．
【答案】C
【分析】以AC、BD交点O为坐标原点，射线OA、OB、OP为x、y、z轴正方向建立空间直角坐标系，设，，，， (a、b>0)，进而写出、、、坐标，可得，，由四点共面有，设，求值即可得答案.
【详解】解：建立如图所示空间直角坐标系，设，，，， (a、b>0)，则，，，，
∴，，
由题意四点共面，则有，其中，
设，
∴
由方程组，即，解得，
所以，
故选：C.
14．（2024·江西·二模）在四棱锥中，棱长为2的侧棱垂直底面边长为2的正方形，为棱的中点，过直线的平面分别与侧棱、相交于点、，当时，截面的面积为（ ）
A．B．2C．D．3
【答案】A
【分析】建立空间直角坐标系，利用向量共面确定点的坐标，利用向量数量积及三角形面积公式即可求出.
【详解】由题意，平面，四边形为正方形，
如图，建立空间直角坐标系D-xyz，

则，，，，，，，
设，，则，
又，，所以，则，
由题意，四点共面，所以，
所以，解得，
所以，，所以，
所以，即，
所以，
所以，
又，
所以，即，
所以，
所以，
所以截面的面积为.
故选：A
二、多选题
15．（2024高二下·浙江·期中）空间直角坐标系中，已知，，，，则（ ）
A．
B．是等腰直角三角形
C．与平行的单位向量的坐标为或
D．在方向上的投影向量的坐标为
【答案】AC
【分析】本题考查空间向量的坐标运算，利用向量的加减法得出坐标，再利用向量的模长公式，可判断A选项；计算出三角形三条边长，可判断B选项；与已知向量平行的单位向量计算公式：可判断C选项；根据在方向上的投影向量与向量共线的性质，可判断D选项.
【详解】根据空间向量的线性运算，
，选项A正确；
计算可得，三条边不相等，选项B不正确；
与平行的单位向量为：
选项C正确；
在方向上的投影向量与向量共线，，选项D不正确，
故选：AC.
16．（2024·广东佛山·二模）四面体中，，，，，，平面与平面的夹角为，则的值可能为（ ）
A．B．C．D．
【答案】AD
【分析】根据给定条件，利用空间向量数量积运算律求解判断作答.
【详解】在四面体中，，，则是二面角的平面角，如图，
，而，，，
，
因为平面与平面的夹角为，则当时，，
当时，，
所以的值可能为，.
故选：AD
三、填空题
17．（2024·上海金山·二模）已知向量，向量，则与的夹角的大小为 .
【答案】
【分析】利用向量夹角的坐标表示来求解.
【详解】因为，，
所以，
因为，所以.
故答案为：.
18．（2024高二上·北京西城·期中）已知平面的法向量为，平面的法向量为，若，则 ．
【答案】
【分析】根据，可得两平面的法向量共线，再根据空间向量的共线定理即可得解.
【详解】因为，
所以两平面的法向量共线，
所以存在唯一实数，使得，
所以，解得，
所以.
故答案为：.
19．（2024高二上·山西·开学考试）已知直线的方向向量是，平面的法向量是，与的位置关系为 .
【答案】或
【分析】利用空间向量法判断线面关系即可得解.
【详解】因为直线的方向向量是，平面的法向量是，
而，
所以，则或.
故答案为：或.
20．（2024高二下·天津蓟州·期中）已知点A（1，2，3），B（0，1，2），C（﹣1，0，λ），若A，B，C三点共线，则 ．
【答案】1
【分析】利用坐标表示向量，由向量共线列方程求出λ的值．
【详解】由题意，点A（1，2，3），B（0，1，2），C（﹣1，0，λ），
所以,
若A，B，C三点共线，则，即，解得.
故答案为：1．
21．（2024高二上·湖南株洲·阶段练习）已知向量，若，则 ．
【答案】
【分析】设，依题意可得，再根据向量夹角公式即可求解.
【详解】设向量，
，，设与的夹角为，，
，.
故答案为：.
22．（2024高二上·北京·期中）直线的方向向量为，直线的方向向量为，平面的法向量为，，，则、、的值依次为 .
【答案】、、
【分析】依题意可得、，即可求出、、的值.
【详解】因为，直线的方向向量为，直线的方向向量为，
所以，则，即，解得，
因为，直线的方向向量为，平面的法向量为，
所以，所以，即，所以，解得，
则、、的值依次为、、.
故答案为：、、
23．（2024高二上·浙江台州·阶段练习）如图，三棱锥中，平面ABC，，且，．若D是棱PC上的点，满足，且，则 ．
【答案】
【分析】证明出两两垂直，建立空间直角坐标系，设，从而由垂直关系得到方程，求出的值.
【详解】因为平面ABC，平面，
所以，又，
故两两垂直，以为坐标原点，所在直线分别为轴，
平行于的直线为轴，建立空间直角坐标系，
故，
因为，所以，
因为，
所以，
解得，负值舍去.
故答案为：
24．（2024高二上·江西宜春·阶段练习）如图所示，在正方体中，E是棱DD1的三等分点（靠近点），点F在棱C1D1上，且，若∥平面，则 .
【答案】
【分析】建立空间直角坐标系，利用向量垂直即可求解.
【详解】建立如图所示的空间直角坐标系，不妨设正方体的棱长为3，
，设，
所以设平面的法向量为，
所以，取，则，
，
由于∥平面，所以，即，
故，所以
所以，
故答案为：
四、解答题
25．（2024高三·全国·专题练习）如图，在四棱锥中，底面，底面是矩形，，分别是的中点，.证明：.
【答案】证明见解析
【分析】建立空间直角坐标系，可证明，进而即可得证.
【详解】证明：由题意，底面，，
如图，以为坐标原点，的方向分别为轴的正方向，建立空间直角坐标系，
则，
由，则，所以，
所以.
因为，所以.
26．（2024高二下·江苏·课后作业）在正方体中，分别是的中点，试建立适当的空间直角坐标系，求证：平面平面.
【答案】证明见解析
【分析】根据正方体的结构特征，以为坐标原点建立空间直角坐标系，利用向量的坐标运算证明线线平行，由面面平行的判定定理证明平面平面.
【详解】证明: 如图，以为坐标原点，所在直线分别为x轴、y轴、z轴，
建立空间直角坐标系．设正方体的棱长为1，
则有，，， ， ， ，
于是， ，，，
显然有，，所以，，
由，平面，平面，平面，
同理平面， 平面，，
所以平面平面
27．（2024高一·全国·专题练习）如图所示，正四棱的底面边长1，侧棱长4，中点为，中点为．求证：平面平面.

【答案】证明见解析
【分析】以为原点，，，所在直线为坐标轴，建立空间直角坐标系，利用向量法证，同理，再结合面面平行判定定理即可证明结论.
【详解】以为原点，，，所在直线为坐标轴，建立空间直角坐标系，如图
则,0,，,1,，,0,，,0,，,1,，,1,，
，，同理，
平面，平面，平面，
平面，平面，平面，
又平面
平面与平面平行．
28．（2024高三·全国·对口高考）如图所示的几何体中，四边形是等腰梯形，，，平面，，.

(1)求二面角的余弦值；
(2)在线段AB（含端点）上，是否存在一点P，使得平面.若存在，求出的值；若不存在，请说明理由.
【答案】(1)
(2)存在，
【分析】（1）建立空间直角坐标系，利用法向量的夹角即可求解二面角，
（2）由平面法向量与直线方向向量垂直，结合向量共线，即可由坐标运算求解.
【详解】（1）过作于，由于，则,由于,且四边形是等腰梯形，所以,在三角形中，由余弦定理可得，所以,故,

以为坐标原点，，为轴，轴，过点作的平行线为轴，建立空间直角坐标系，设，则，

设面的法向量，
则，即，取，得．
设面的法向量，
则，即，则取，得．
，
由几何体的特征可知二面角的平面角为锐角，
二面角的余弦值为．
（2），,， 面，
面．
设,
若平面，则 ,所以，
所以
29．（2024高一·全国·专题练习）如图，且，，且，且，平面ABCD，.若M为CF的中点，N为EG的中点，求证：平面CDE；
【答案】证明见解析
【分析】建立空间直角坐标系，由空间向量判断位置关系
【详解】因为，，平面ABCD，
而AD､平面ABCD，所以，，
因此以D为坐标原点，分别以､､的方向为x轴，y轴，z轴的正方向建立空间直角坐标系.
因为且，且，，
所以，，，，，，，，.
设为平面CDE的法向量，，，
则，不妨令，可得；
又，所以.
又∵直线平面CDE，∴平面CDE；
30．（2024高二上·广东广州·阶段练习）如图，在正方体中，E，F分别是，的中点．
(1)求证：；
(2)求证：平面
【答案】(1)见解析；
(2)见解析.
【分析】建立合适的空间直角坐标系，利用空间向量研究空间位置关系即可.
【详解】（1）
如图所示，以D为原点建立空间直角坐标系，设正方体边长为2，
则，所以，
有；
（2）由（1）知，设平面的一个法向量为，
则，
令，即，
又，显然，
故平面.
31．（2024高二下·江苏·课后作业）已知棱长为1的正方体在空间直角坐标系中的位置如图所示，分别为棱的中点，求证：.
【答案】证明见解析
【分析】由图中的空间直角坐标系，求出相关点的坐标，证明，可得.
【详解】因为正方体的棱长为1， 分别为棱的中点，
所以有， ， ， ，
所以，，则有，所以.
32．（2024高二·全国·专题练习）如图所示，平面平面，四边形为正方形，是直角三角形，且，，，分别是线段，，的中点，求证：平面平面．
【答案】证明见解析
【分析】建立空间直角坐标系，利用法向量即可求解.
【详解】因为平面PAD⊥平面ABCD，四边形ABCD为正方形，△PAD是直角三角形，
所以AB，AP，AD两两垂直，
以A为坐标原点，AB，AD，AP所在直线分别为x轴，y轴，z轴，建立空间直角坐标系，
则．
所以，，，，
设是平面EFG的法向量，
则，，即，得，
令，则，，所以，
设是平面PBC的法向量，
由，，即，得，
令，则，，所以，
所以，所以平面EFG∥平面PBC．
33．（2024高三·全国·专题练习）如图，在几何体ABCDE中，ABC，BCD，CDE均为边长为2的等边三角形，平面ABC⊥平面BCD，平面DCE⊥平面BCD．求证：A，B，D，E四点共面；
【答案】证明见解析
【分析】取的中点，连接，取的中点，连接，证明平面，平面，得两两垂直，以为坐标原点，所在直线为轴，所在直线为轴，所在直线为轴建立如图所示的空间直角坐标系，写出各点坐标，设，由求得点坐标，证明向量共面，得证四点共面．
【详解】
取的中点，连接，取的中点，连接，
因为平面平面，且平面平面，
而为等边三角形，所以，因此平面，
因为平面平面，且平面平面，
又因为为等边三角形，所以，因此平面，
又因为平面，因此，
又因为为等边三角形，所以，因此两两垂直，
从而以为坐标原点，所在直线为轴，所在直线为轴，所在直线为轴建立如图所示的空间直角坐标系，
又因为均为边长为2的等边三角形，所以，，，
设，则，，，
由于，所以，解得，
因此，所以，，，
所以，由空间向量基本定理可知：共面，所以四点共面；
34．（2024高三·全国·专题练习）如图，直三棱柱中，，，，D为BC的中点，E为上的点，且．求证：平面；
【答案】证明见解析
【分析】以点为原点，射线的方向分别为轴正方向，建立空间直角坐标系，得到，再论证即可.
【详解】证明：在直三棱柱中，，显然射线两两垂直，
以点为原点，射线的方向分别为轴正方向，建立空间直角坐标系，如图，
因为，，D为BC的中点，E为上的点，且，
则，，
于是，即，
而平面，
所以平面.
35．（2024高三·全国·专题练习）如图，直三棱柱的侧面为正方形，，E，F分别为，的中点，．证明：平面；
【答案】证明见解析
【分析】由题意可得两两垂直，所以以为坐标原点，分别为轴，建立空间直角坐标系，利用空间向量证明即可.
【详解】证明：因为三棱柱为直三棱柱，
所以，
又因为，，所以，
因为，平面，
所以平面，
因为平面，所以，
因为为正方形，所以，
所以两两垂直，
所以以为坐标原点，分别为轴，建立空间直角坐标系，
则，
因为，，
所以，，
因为平面，，
所以平面，
36．（2024高三·全国·专题练习）在正方体中，如图、分别是，的中点．求证：平面平面；
【答案】证明见解析
【分析】设棱长为，以为原点，建立如图所示的空间直角坐标系，利用空间向量证明即可.
【详解】证明：设棱长为，以为原点，建立如图所示的空间直角坐标系，
则，，，，，
所以，，，，
设平面的法向量，
则，取，得，
设平面的法向量，
则，取，得，
所以，所以，
则平面平面．
37．（2024高二·全国·专题练习）如图，正三棱柱中，分别是棱上的点，.

证明：平面平面.
【答案】证明见解析
【分析】建立空间直角坐标系，求解两个平面的法向量，利用法向量证明面面垂直.
【详解】证明：取的中点，连接，

在正三棱柱中，不妨设;
以为原点，分别为轴和轴正方向，建立空间直角坐标系，如图所示，
则,，
；
设平面的一个法向量为，
则，取，则，，即；
设平面的一个法向量为，
则，取，得，，即.
因为，所以平面平面；
38．（2024高三·全国·专题练习）已知直三棱柱中，侧面为正方形，，E，F分别为AC和的中点，D为棱上的动点..证明：；
【答案】证明见解析
【分析】由题意可证得两两垂直，所以以为原点，分别以所在直线为轴建立空间直角坐标系，然后利用空间向量证是即可.
【详解】证明：因为三棱柱是直三棱柱，所以底面，
又底面，所以，，
又因为，，所以，
又，平面，所以平面，
又平面，所以，即两两垂直，
以为原点，分别以所在直线为轴建立空间直角坐标系，设，则
，，，，，，，，
设，所以，，
因为，
所以，即.
39．（2024高三·全国·专题练习）如图，在四棱锥中，底面ABCD是菱形，，，，底面ABCD，，点E在棱PD上，且.证明：平面平面ACE；
【答案】证明见解析
【分析】
由题意可得BO，CO，PO互相垂直，所以以O为坐标原点，所在的直线分别为轴建立空间直角坐标系，然后利用空间向量证明即可.
【详解】证明：因为底面ABCD是菱形，所以，
因为平面ABCD，平面，
所以，
所以BO，CO，PO互相垂直，
所以以点O为坐标原点，所在的直线分别为轴建立如图所示空间直角坐标系，
由，，可知相关点坐标如下：
，，，，，
因为平面，
所以平面
所以平面PBD的一个法向量为，
因为，所以，
故平面PBD，
因为平面，
所以平面平面ACE.
40．（2024高三·全国·专题练习）如图，在三棱柱中，平面ABC，，，D为的中点，交于点E．证明：.
【答案】证明见解析
【分析】由题意可得两两垂直，所以以为原点，所在的直线分别为轴建立空间直角坐标系，然后利用空间向量证明即可.
【详解】因为平面，平面‖平面,
所以平面，
因为平面，所以,
因为，所以两两垂直，
所以以为原点，所在的直线分别为轴建立如图所示的空间直角坐标系，
则，
所以，
所以，所以，
故
41．（2024高三·全国·专题练习）如图，在底面是矩形的四棱锥中，平面，，，是PD的中点.
求证：平面平面.
【答案】证明见解析
【分析】由题意可得两两垂直，所以以为原点，以所在的直线分别为轴建立空间直角坐标系，利用空间向量证明即可.
【详解】证明：因为平面，平面，
所以，
因为四边形为矩形，所以，
所以两两垂直，所以以为原点，以所在的直线分别为轴建立空间直角坐标系，如图所示
则
所以
所以即，
所以即，
又，平面PAD，
所以平面PAD，
又平面，所以平面平面PAD.
42．（2024高三·全国·专题练习）如图，棱台中，，底面ABCD是边长为4的正方形，底面是边长为2的正方形，连接，BD，.证明：.
【答案】证明见解析
【分析】连接交于，以所在直线为轴，经过且垂直于平面的直线为轴，交上底面于，连接，建立空间直角坐标系如图，然后利用空间向量证明即可
【详解】证明：由题意，该棱台是正四棱台.
连接交于，以所在直线为轴，经过且垂直于平面的直线为轴，交上底面于，连接，建立空间直角坐标系如图.
根据正四棱台的性质，过作底面的垂线，则垂足在上.
由题意得，为上底面正方形对角线长的一半，
显然，故，又，
则，故.
于是，，
则，所以.
43．（2024·云南曲靖·模拟预测）如图，已知四棱锥的底面是平行四边形，侧面是等边三角形，.
(1)求证：平面平面；
(2)设为侧棱上一点，四边形是过两点的截面，且平面，是否存在点，使得平面平面？若存在，求的值；若不存在，说明理由.
【答案】(1)证明见解析
(2)存在，
【分析】（1）根据题意，先由线面垂直的判定定理得到平面，从而得到面面垂直；
（2）根据题意，以为坐标原点，建立空间直角坐标系，然后结合法向量与空间向量的坐标运算，代入计算，即可得到结果.
【详解】（1）证明：在中，因，
所以，所以，又，
且，平面，所以平面，
又平面，
所以平面平面.
（2）假设存在点，使得平面平面.
取中点为，连接，则，
因为平面平面，
平面平面，
所以平面.
如图所示建立空间直角坐标系，
不妨设，则，，则，
设是平面的法向量，则，取.
设，其中.
则
连接，因平面平面，平面平面，故取与同向的单位向量.
设是平面的法向量，
则，取.
由平面平面，知，有，解得.
故在侧棱上存在点，使得平面平面.
44．（2024高三·全国·专题练习）斜三棱柱的各棱长都为，点在下底面的投影为的中点.在棱（含端点）上是否存在一点使？若存在，求出的长；若不存在，请说明理由；
【答案】存在，
【分析】连接，以为原点建立如图所示空间直角坐标系，设，根据结合空间向量的坐标运算求解.
【详解】因为点在下底面的投影为的中点，故平面，
连接，由题意为正三角形，故，
以为原点，分别为轴建立如图所示空间直角坐标系，
则，，
可得，，，
设，
可得，
假设在棱（含端点）上存在一点使，
则，解得，
所以存在，此时.
45．（2024高三·全国·专题练习）斜三棱柱的各棱长都为2，，点在下底面ABC的投影为AB的中点O．在棱（含端点）上是否存在一点D使？若存在，求出BD的长；若不存在，请说明理由；
【答案】存在，
【分析】连接，以O点为原点，以所在直线为轴建立空间直角坐标系，设，根据求解即可.
【详解】连接，因为，为的中点，所以，
由题意知平面ABC，，
又，，所以，
以O点为原点，以所在直线为轴建立空间直角坐标系，如图，
则，，，，
由得，同理得，
设，得，
又，，
由，则，可得，
得，又，即，
所以存在点D且满足条件.
46．（2024·河北保定·一模）如图，平行六面体的所有棱长均为，底面为正方形，，点为的中点，点为的中点，动点在平面内．
(1)若为中点，求证：；
(2)若平面，求线段长度的最小值．
【答案】(1)证明见解析
(2)
【分析】（1）由条件先求，，，再证明，由此完成证明；
（2）建立空间直角坐标系，设，求平面的法向量和直线的方向向量，由条件列方程确定的关系，再求的最小值即可.
【详解】（1）由已知，，，，
所以，
，
，
因为为中点，
所以，
又，
所以，
所以
所以
（2）连接，，
∵，
∴，
∵，
∴，
连接，
由正方形的性质可得三点共线，为的中点，
所以，
由第一问，
平面，，
所以平面，
以为坐标原点， 所在直线为轴，轴，轴建立空间直角坐标系
、、、、
，
设平面法向量为，，
则，所以，
∴，
令，则，．
∴为平面的一个法向量，
因为点在平面内，
故设点的坐标为，
因为，
所以，
，则，
所以，
所以当时，有最小值，最小值为.
47．（2024高二上·北京海淀·期中）已知三棱锥（如图1）的平面展开图（如图2）中，四边形为边长为的正方形，和均为正三角形.在三棱锥中：
(1)求点到平面的距离；
(2)若点在棱上，满足，点在棱上，且，求的取值范围.
【答案】(1)
(2)
【分析】（1）根据四边形为正方形，得到，再利用勾股定理得到，即可证得平面，然后利用等体积的方法即可求得点到平面的距离；
（2）建立空间直角坐标系，通过设，，得到和的坐标，再利用列等式，得到的关系，根据的范围即可得到的范围.
【详解】（1）
如图，取，中点，，连接，，，
∵展开图中四边形为边长为的正方形，为中点，
∴，，
又和均为正三角形，∴，，
∵，∴，
∵，平面，平面,
∴平面，
设点到平面的距离为，
，解得，
所以点到平面的距离为.
（2）
如图，以为原点，分别以为轴建立空间直角坐标系，
，，，，，，,
∵，∴，，
设，则,
∵，∴，整理得，
∵，∴，
∴的范围为.
48．（2024高三·全国·专题练习）如图，在四棱锥中，底面ABCD为正方形，平面ABCD，E为PD的中点，.求证：PB平面AEC；
【答案】证明见解析
【分析】由题意可得AB，AD，AP两两互相垂直，所以以A为原点，以AB，AD，AP分别为x轴，y轴，z轴，建立空间直角坐标系，然后利用空间向量证明即可.
【详解】证明：因为平面ABCD，且平面ABCD，则，
因为四边形ABCD为正方形，所以，
所以AB，AD，AP两两互相垂直，
如图，以A为原点，以AB，AD，AP分别为x轴，y轴，z轴，建立空间直角坐标系，
则，
可得，，.
设平面AEC的法向量为，
则，取，可得，
所以平面AEC的一个法向量为，
可知，即，
又因为平面AEC，所以PB//平面AEC，
49．（2024高二上·山东聊城·阶段练习）如图，正方形与梯形所在平面互相垂直，已知，，．

(1)求证：平面．
(2)线段上是否存在点M，使平面平面？若存在，求出的值；若不存在，请说明理由．
【答案】(1)证明见解析
(2)存在，
【分析】（1）根据线面平行、面面平行的判定定理，结合面面平行的性质定理进行证明即可；
（2）根据面面垂直的性质，结合正方形的性质建立空间直角坐标系，根据空间向量数量积的运算性质，结合面面垂直的判定定理进行求解即可.
【详解】（1）证明：因为，平面，平面，所以平面，
同理，平面，
又，所以平面平面，
因为平面，
所以平面.
（2）因为平面平面，
平面平面，，
平面，所以平面，
又平面，故.
而四边形是正方形，所以，又，
以为原点，，，所在直线分别为轴，轴，轴，建立空间直
角坐标系.
设，则，，，，，
，，，，
设平面的一个法向量，则，即，
令，则，所以.
若与重合，则平面的一个法向量，
则，则此时平面与平面不垂直.
若与不重合，如图：

设，则，,
设平面的一个法向量，则，
即，令，则，，
所以，
平面平面等价于，即，
得.
所以，线段上存在点使平面平面，且.
50．（2024高二·阶段练习）如图，在四棱锥中，平面，，，，点为棱的中点．证明：

(1)平面；
(2)平面⊥平面．
【答案】(1)证明见解析
(2)证明见解析
【分析】（1）由题意可以点为原点，以分别为轴建立如图所示的空间直角坐标系，求出直线的方向向量和平面的法向量，由，即可证明；
（2）求出平面的一个法向量，由即可证明.
【详解】（1）因为平面，且平面，所以，
又因为，且平面，所以平面，
依题意，以点为原点，以分别为轴建立如图所示的空间直角坐标系，

则，，
由为棱的中点，得，则，
所以为平面的一个法向量，
又，所以，
又平面，所以平面．
（2）由（1）知平面的法向量，，，
设平面的一个法向量为，
则，即，令，可得，所以，
又，
所以，所以平面⊥平面．
51．（2024高三·全国·专题练习）在苏州博物馆有一类典型建筑八角亭，既美观又利于采光，其中一角如图所示，为多面体，，，，底面，四边形是边长为2的正方形且平行于底面，，，的中点分别为，，，．证明：//平面；

【答案】证明见解析
【分析】过点作的平行线，然后以为原点，建立如图所示空间直角坐标系，利用空间向量证明即可.
【详解】证明：过点作的平行线，由题意可知以为原点，建立如图所示空间直角坐标系，

则，，，，，，，，，
因为，的中点分别为，，
所以，，则，
设平面的法向量为，，，
则，，令，则，
因为，
所以，
因为平面，
所以平面.
52．（2024高二上·广东佛山·阶段练习）如图，在正方体中，分别是的中点

(1)证明：平面.
(2)在直线上是否存在点，使得平面？若存在，请指出的位置；若不存在.请说明理由.
【答案】(1)见解析
(2)存在，满足，理由见解析
【分析】（1）建立空间直角坐标系出，利用向量垂直的坐标表示及线面垂直判定定理求证；
（2）根据向量法判断线面是否平行即可.
【详解】（1）以D为坐标原点，分别以为轴建立空间直角坐标系，如图，

则，
由中点坐标公式可得，
则，，，
，
，
，，
即，，
又，平面，
平面.
（2）假设存在，使平面，设，
则，
由（1）知，是平面的一个法向量，
则，
解得，
故存在，满足，使平面.
53．（2024高三·全国·专题练习）在四棱锥中，平面ABCD⊥平面PCD，底面ABCD为梯形．，，且，，．若M是棱PA的中点，则对于棱BC上是否存在一点F，使得MF与PC平行．

【答案】不存在
【分析】以为原点，以所在的直线分别为轴、轴和轴，建立空间直角坐标系，假设上存在点，使得，设，其中，根据，列出方程组，即可得出结论.
【详解】解：在平面内过点作，交于点，
因为平面平面，且平面平面，平面，
可得平面，
又由，所以两两垂直，
以为原点，以所在的直线分别为轴、轴和轴，建立空间直角坐标系，如图所示，
由，，，
可得，
假设上存在点，使得，
设，其中，
因为是棱的中点，可得，
又由，
所以，
设，可得，此方程组无解，所以假设不成立，
所以对于上任意一点，与都不平行，
即在线段上不存在点，使得与平行．

54．（2024高二上·山西大同·期中）如图，在直三棱柱中，，垂足为，为线段上的一点.

(1)若为线段的中点，证明：平面；
(2)若平面平面，求的值.
【答案】(1)证明见解析；
(2)
【分析】（1）利用棱长求出，进而得到D是中点，利用中位线证明，进而证明线面平行；
（2）建立空间直角坐标系，根据面面垂直时两个面的法向量也互相垂直，列出方程进行求解即可.
【详解】（1）连接，在直三棱柱中，有，
.
为中点，
又为中点，，
，，
又平面平面，
平面.
（2）建立如图所示的空间直角坐标系，则，
，
设，
则，
设平面的法向量，
则，取，得，
设平面的法向量，
则，取，得，
平面平面，
，解得，
当平面平面时，.
55．（2024高二下·江苏·课后作业）如图，四边形ABCD和ABEF都是平行四边形，且不共面，M，N分别是AC，BF的中点，求证：.
【答案】证明见解析.
【分析】根据给定条件，利用空间向量的线性运算，计算判断与共线即可推理作答.
【详解】（方法1）因为M，N分别是AC，BF的中点，且四边形ABCD和ABEF都是平行四边形，
则有，又，
两式相加得：，因此与共线，而直线与不重合，
所以.
（方法2）因为M，N分别是AC，BF的中点，且四边形ABCD和ABEF都是平行四边形，
，
因此与共线，而直线与不重合，
所以.
56．（2024高二·全国·课后作业）如图，在平行六面体中，，．
(1)求证：、、三点共线；
(2)若点是平行四边形的中心，求证：、、三点共线．
【答案】(1)证明见解析
(2)证明见解析
【分析】（1）根据空间向量的加减运算，选定基底表示出向量，根据向量间的倍数关系可证明结论；
（2）根据空间向量的加减运算，选定基底表示出向量，根据向量间的倍数关系可证明结论；
【详解】（1）由题意，，，
故
,
,
故，由于有公共点A，
故A、、三点共线；
（2）由题意，点是平行四边形的中心，
故
，
故 ,因为有公共点D，
故、、三点共线．
57．（2024高二上·湖北宜昌·期中）如图，在棱长为2的正方体中，点分别是线段的中点.

(1)求证：
(2)求三棱锥的体积.
【答案】(1)证明见解析
(2)
【分析】（1）首先建立空集直角坐标系，分别求和的坐标，利用向量平行，即可证明线线平行；
（2）首先利用向量公式求点到平面的距离，再代入体积公式，即可求解.
【详解】（1）建立如图所示的空间直角坐标系，

，
所以，显然，易知两者不共线，
所以有；
（2）由（1）可得：，
所以，
设平面的法向量为，
所以有，
因此点到平面的距离为，
在等腰三角形中，，
所以等腰三角形的面积为，
所以三棱锥的体积为
58．（2024高三·全国·专题练习）如图四棱锥，且，平面平面，且是以为直角的等腰直角三角形，其中为棱的中点，点在棱上，且.求证：四点共面.
【答案】证明见解析
【分析】建立空间直角坐标系，根据条件写出相应点的坐标，利用空间向量基本定理即可求证即可.
【详解】证明：由，且，
取的中点，连接，则，且，
所以，
又是以为直角的等腰直角三角形，所以.
过点作，垂足为，则点为的中点，且，
因为平面平面，且平面平面，
所以平面，
故以所在的直线分别为轴，轴，过点作垂直于平面的轴，建立如图所示空间直角坐标系，
则，，，
因为为棱的中点，所以，又因为点在棱上，且，
所以，则，，，
令，
则，
则，解得，
故，则共面，且向量有公共点，
所以四点共面.
59．（2024高二上·河北邢台·阶段练习）如图，在边长为3的正方体中，点P，Q，R分别在棱，，上，且.
（1）求点D到平面的距离；
（2）若平面与线段的交点为N，求的值.
【答案】（1）；（2）.
【分析】（1）建立空间坐标系，求得平面的法向量，利用空间向量中点到面的距离公式求解即可.
（2）设，设，根据共线定理和共面定理列方程，解出，，进而求得，从而得出的值．
【详解】（1）如图，以点D为坐标原点，分别以，，的方向为x，y，z轴的正方向，建立空间直角坐标系，则，，，，，，，，，.
设平面的法向量为，
则，代入可得，
令，则，，所以，
故点D到平面的距离为.
（2）因为点N在平面内，可设（其中m，n为常数），
又与共线，可设，由图可得，
即，
整理得，
由①③可得④，
由②③可得⑤，
联立④⑤解得，代入②可得，
所以，即.
60．（2024高三·全国·专题练习）已知E，F，G，H分别是空间四边形ABCD的边AB，BC，CD，DA的中点，用向量法证明：
(1)E，F，G，H四点共面；
(2)平面EFGH．
【答案】(1)证明见解析
(2)证明见解析
【分析】（1）要证E，F，G，H四点共面，只需证明向量，，共面，结合向量的线性运算及共面向量定理证明即可；
（2）由向量共线结合线面平行的判定定理证明．
【详解】（1）如图，连接EG，BG．

因为＝＋＝＋(＋)＝＋＋＝＋，
由向量共面的充要条件可知，向量，，共面，
又，，过同一点E，从而E，F，G，H四点共面．
（2）因为＝－＝－＝(－)＝，
又E，H，B，D四点不共线，所以EH//BD，
又EH⊂平面EFGH，BD⊄平面EFGH，
所以BD//平面EFGH．
61．（2024·四川泸州·模拟预测）如图，四边形为正方形，若平面平面，，，.
(1)求二面角A－CF－D的余弦值；
(2)判断点D与平面CEF的位置关系，并说明理由.
【答案】(1)
(2)点在平面外，证明见解析
【分析】（1）设出相应线段的长度，进而建立空间直角坐标系，利用空间向量夹角公式求得答案；
（2）根据空间向量共面定理即可判断.
【详解】（1）因为平面平面，且交线为，
因为四边形为正方形，所以，于是平面，
以为原点，所在方向分别为轴，轴的正方向建立空间直角坐标系.
设，容易得到，
所以，，，，
，，设平面的法向量为，
由，可取，
又，，设平面的法向量为，
由，可取，
所以，
所以二面角的的余弦值为.
（2）点在平面外，证明如下，连接ED，
因为，，，
设，则，
即，显然此方程组无解，
所以四点，，，不共面，即点在平面外.
62．（2024·河南郑州·一模）如图，正四棱锥的底面边长和高均为2，，分别为，的中点．
(1)若点是线段上的点，且，判断点是否在平面内，并证明你的结论；
(2)求直线与平面所成角的正弦值．
【答案】(1)点在平面内，证明见解析
(2)
【分析】（1）连接、交于，连接，以为坐标原点，、、为、、轴建立空间直角坐标系，求出、、，即可得到，从而得到、、、四点共面，即可得证；
（2）利用空间向量法计算可得.
【详解】（1）解：连接、交于，连接，由正四棱锥的性质可得平面，底面为正方形，则，
所以以为坐标原点，、、为、、轴建立空间直角坐标系，
则，，，
所以，，
又，得，，
所以，
所以、、、四点共面，即点在平面内．
（2）解：由（1）可得，
设平面的法向量，由，得，
令，则，，所以，
所以，
所以直线与平面所成角的正弦值为．
63．（2024·江苏·三模）如图，三棱锥P－ABC的底面为等腰直角三角形，∠ABC＝90°，AB＝2．D，E分别为AC，BC的中点，PD⊥平面ABC，点M在线段PE上．
(1)再从条件①、②、③、④四个条件中选择两个作为已知，使得平面MBD⊥平面PBC，并给予证明；
(2)在（1）的条件下，求直线BP与平面MBD所成的角的正弦值．
条件①：；
条件②：∠PED＝60°；
条件③：PM＝3ME：
条件④：PE＝3ME．
【答案】(1)答案见解析
(2)答案见解析
【分析】（1）如图，建立以D为原点的空间直角坐标系，设，，由平面MBD⊥平面PBC，可得两平面法向量互相垂直，即可得，据此可知可选择①④或②③；
（2）由（1）所建立空间直角坐标系及平面MBD法向量，利用向量方法可得答案.
【详解】（1）因PD⊥平面ABC，平面ABC，平面ABC，则，
又由题可知，则如图，建立以D为原点的空间直角坐标系，
则，，，，
设，.
则，，，，.
故.
设平面MBD法向量为，
则，令，可得；
设平面PBC法向量为，
则，可令，可得.
要使平面MBD⊥平面PBC，需满足.
注意到条件①，
PD⊥平面ABC，平面ABC，，又由题可知，则条件②，
条件③，条件④.
则当条件①④成立或条件②③成立时，都有，即可以使平面MBD⊥平面PBC；
（2）由（1），当选择①④时，，，.
则，平面MBD法向量为，
设BP与平面MBD所成角为，则；
当选择②③时，，，.
则，平面MBD法向量，
设BP与平面MBD所成角为，则；
成套的课件成套的教案成套的试题成套的微专题尽在高中数学同步资源大全QQ群552511468也可联系微信fjshuxue加入百度网盘群1.5T一线老师必备资料一键转存自动更新永不过期
名称
定义
空间向量
在空间中，具有大小和方向的量
相等向量
方向相同且模相等的向量
相反向量
长度相等而方向相反的向量
共线向量(或平行向量)
表示若干空间向量的有向线段所在的直线互相平行或重合的向量
共面向量
平行于同一个平面的向量
向量表示
坐标表示
数量积
a·b
a1b1＋a2b2＋a3b3
共线
a＝λb(b≠0，λ∈R)
a1＝λb1，a2＝λb2，a3＝λb3
垂直
a·b＝0(a≠0，b≠0)
a1b1＋a2b2＋a3b3＝0
模
|a|
eq \r(a\\al(2,1)＋a\\al(2,2)＋a\\al(2,3))
夹角余弦值
cs〈a，b〉＝eq \f(a·b,|a||b|)(a≠0，b≠0)
cs〈a，b〉＝eq \f(a1b1＋a2b2＋a3b3,\r(a\\al(2,1)＋a\\al(2,2)＋a\\al(2,3))·\r(b\\al(2,1)＋b\\al(2,2)＋b\\al(2,3)))
位置关系
向量表示
直线l1，l2的方向向量分别为n1，n2
l1∥l2
n1∥n2⇔n1＝λn2(λ∈R)
l1⊥l2
n1⊥n2⇔n1·n2＝0
直线l的方向向量为n，平面α的法向量为m，l⊄α
l∥α
n⊥m⇔n·m＝0
l⊥α
n∥m⇔n＝λm(λ∈R)
平面α，β的法向量分别为n，m
α∥β
n∥m⇔n＝λm(λ∈R)
α⊥β
n⊥m⇔n·m＝0
（一）
用已知向量表示某一向量的三个关键点
(1)要结合图形，以图形为指导是解题的关键．
(2)要正确理解向量加法、减法与数乘运算的几何意义．
(3)在立体几何中，三角形法则、平行四边形法则仍然成立．
题型1：空间向量的线性运算
1-1．（福建省福州十五中、格致鼓山中学、教院二附中、福州铜盘中学、福州十中2023-2024学年高二上学期期中联考数学试题）如图，空间四边形中，，点在上，且，点为中点，则（ ）
A．B．
C．D．
【答案】B
【分析】根据给定的几何体，利用空间向量的线性运算求解即得.
【详解】依题意，
.
故选：B
1-2．（2024·福建福州·三模）在三棱锥P-ABC中，点O为△ABC的重心，点D，E，F分别为侧棱PA，PB，PC的中点，若，，，则=（ ）
A．B．C．D．
【答案】D
【分析】根据空间向量的线性运算，结合重心的性质即可求解.
【详解】取中点为，
三个式子相加可得,
又
,
故选：D

1-3．（上海市南洋模范中学2023-2024学年高二上学期期中数学试题）如图所示，在平行六面体中，为与的交点，若，则（ ）

A．B．
C．D．
【答案】D
【分析】利用空间向量的线性运算进行求解.
【详解】.
故选：D
1-4．（2024高二上·陕西西安·期末）如图，在四面体中，是的重心，是上的一点，且，若，则为（ ）
A．B．
C．D．
【答案】D
【分析】根据空间向量线性运算进行计算，用表示出．
【详解】因为是中点，所以，
是的重心，则，
所以，
因为
所以，
若，则．
故选：D．
【点睛】本题考查空间的向量的线性运算，掌握向量线性运算的运算法则是解题关键．
（二）
应用共线(面)向量定理、证明点共线(面)的方法比较
三点(P，A，B)共线
空间四点(M，P，A，B)共面
eq \(PA,\s\up6(→))＝λeq \(PB,\s\up6(→))
eq \(MP,\s\up6(→))＝xeq \(MA,\s\up6(→))＋yeq \(MB,\s\up6(→))
对空间任一点O，eq \(OP,\s\up6(→))＝eq \(OA,\s\up6(→))＋teq \(AB,\s\up6(→))
对空间任一点O，eq \(OP,\s\up6(→))＝eq \(OM,\s\up6(→))＋xeq \(MA,\s\up6(→))＋yeq \(MB,\s\up6(→))
对空间任一点O，eq \(OP,\s\up6(→))＝xeq \(OA,\s\up6(→))＋(1－x)eq \(OB,\s\up6(→))
对空间任一点O，eq \(OP,\s\up6(→))＝xeq \(OM,\s\up6(→))＋yeq \(OA,\s\up6(→))＋(1－x－y)eq \(OB,\s\up6(→))
题型2：空间向量基本定理及其应用
2-1．（2024高二上·湖南郴州·阶段练习）已知，，如果与为共线向量，则（ ）
A．B．C．D．
【答案】D
【分析】根据空间共线向量的性质进行求解即可.
【详解】因为与为共线向量，
所以，
故选：D
2-2．（2024高二·全国·课后作业）若、、三点共线，则（ ）．
A．
B．
C．
D．
【答案】A
【分析】直接根据求解即可.
【详解】∵，，
由题意得，则，
∴、，∴，
故选:A．
2-3．（湖南省岳阳市平江县2023-2024学年高二上学期1月期末数学试题）已知A、B、C三点不共线，对平面外的任一点O，下列条件中能确定点M与点A、B、C一定共面的是（ ）
A．B．
C．D．
【答案】B
【分析】根据四点共面的性质进行判断即可.
【详解】M与A、B、C共面的条件是，且，
故B选项正确，
故选：B
2-4．（2024高二下·四川雅安·期末）向量，分别是直线，的方向向量，且，，若，则（ ）
A．，B．，
C．，D．，
【答案】C
【分析】根据空间向量平行的坐标运算计算得解.
【详解】因为，所以，所以，，所以，解得，.
故选：C.
2-5．（2024高二下·江苏扬州·期中）已知空间、、、四点共面，且其中任意三点均不共线，设为空间中任意一点，若，则（ ）
A．B．C．D．
【答案】D
【分析】根据空间四点共面的充要条件代入即可解决
【详解】
由、、、四点共面，且其中任意三点均不共线
可得，解之得
故选：D
2-6．（2024高二上·湖南郴州·阶段练习）为空间任意一点，若，若、、、四点共面，则（ ）
A．B．C．D．
【答案】C
【分析】利用空间向量共面基本定理的推论可求出的值.
【详解】空间向量共面的基本定理的推论：，且、、不共线，
若、、、四点共面，则，
因为为空间任意一点，若，且、、、四点共面，
所以，，解得.
故选：C.
2-7．（2024高三·全国·专题练习）已知，若三向量共面，则等于（ ）
A．B．9C．D．
【答案】D
【分析】根据题意利用空间向量共面定理列方程求解即可
【详解】∵，，共面，
∴设（为实数），即，
∴，解得．
故选：D.
2-8．（2024高二·全国·课后作业）在四面体OABC中，点M，N分别为OA、BC的中点，若，且G、M、N三点共线，则 ．
【答案】
【分析】由三点共线得存在实数，使得，再由空间向量的线性运算结合空间向量基本定理求得，即可求解.
【详解】
若G、M、N三点共线，则存在实数，使得，又点M，N分别为OA、BC的中点，则，，则，则，解得，则.
故答案为：.
（三）
空间向量数量积及其应用
空间向量的数量积运算有两条途径，一是根据数量积的定义，利用模与夹角直接计算；二是利用坐标运算．
题型3：空间向量数量积及其应用
3-1．【多选】（2024高二上·辽宁大连·期末）已知向量，，则下列正确的是（ ）
A．B．C．D．
【答案】AB
【分析】根据给定条件，利用空间向量的坐标运算逐项计算判断作答.
【详解】向量，，则，A正确；
显然，B正确；
由数量积的定义得，C错误；
显然，则，即有，D错误.
故选：AB
3-2．（2024高二上·山东济宁·阶段练习）已知是棱长为2的正方体内切球的一条直径，则 ．
【答案】2
【分析】设该正方体的内切球的球心为O，由，结合向量数量积运算求得正确答案.
【详解】因为正方体的棱长为2，所以其内切球的半径．
又球心一定在该正方体的体对角线的中点处，且体对角线长为，
所以设该正方体的内切球的球心为O，则，
易知，
所以．
故答案为：
3-3．（2024·上海松江·二模）已知空间向量，，，若，则 ．
【答案】
【详解】，
，，，
解得，
故答案为：.
3-4．（2024高二上·重庆万州·阶段练习）已知空间向量，，则在方向上的投影向量为 .
【答案】
【分析】首先求得与同向的单位向量，根据投影向量定义知所求为.
【详解】，与同向的单位向量，
在方向上的投影向量为.
故答案为：.
3-5．（2024·黑龙江哈尔滨·模拟预测）如图，平行六面体中，，，，，则线段的长为 .

【答案】1
【分析】根据空间向量的数量积运算律求解即可.
【详解】由题可得, ，,
所以,且,
因为,
所以
，
所以，
故答案为:1.
3-6．【多选】（2024高三上·黑龙江哈尔滨·期中）如图，在平行六面体中，其中以顶点A为端点的三条棱长均为6，且彼此夹角都是，下列说法中不正确的是（ ）

A．
B．
C．向量与夹角是
D．向量与所成角的余弦值为
【答案】CD
【分析】根据题意，利用空间向量的线性运算和数量积运算，对选项中的命题进行分析判断，能求出结果.
【详解】在平行六面体中，其中以顶点为端点的三条棱长均为6 ，且彼此夹角都是，
.
对于A，
，
， A正确；
对于B，
，
，即，B正确；
对于C，连接，由题意可知是等边三角形，则，
，且向量与的夹角是，
向量与夹角是，C错误；
对于D，，
，
，
，D错误.
故选：CD

3-7．【多选】（2024高二上·浙江温州·期末）已知空间向量，，下列说法正确的是（ ）
A．若，则
B．若，则
C．若在上的投影向量为，则
D．若与夹角为锐角，则
【答案】ABD
【分析】对于A：结合向量垂直的性质即可求解；
对于B：结合向量的四则运算即可求解；
对于C：利用投影的几何意义即可求解；
对于D：根据向量的夹角公式即可求解.
【详解】对于A：，，
即：，
解得：.
故A选项正确；
对于B：，
，解得：.
故B选项正确；
对于C：在上的投影向量为：，
即，代入坐标化简可得：，无解，
故C选项错误；
对于D：与夹角为锐角，
，解得：，
且与不共线，即，解得：，
所以与夹角为锐角时，解得：.
故D选项正确；
故选：ABD.
3-8．【多选】（2024·安徽·一模）在平行六面体中，已知，，则（ ）
A．直线与所成的角为
B．线段的长度为
C．直线与所成的角为
D．直线与平面所成角的正弦值为
【答案】AC
【分析】设，将分别用表示，再根据向量数量积的运算律即可判断ABC；对于D，先证明平面平面，从而可得与平面所成的角为，再解即可.
【详解】设，则，且，
对于A，，
，
所以直线与所成的角为，故A正确；
对于B，因为，
所以，故B错误；
对于C，因为，
所以，故C正确；
对于D，连接，交于点，则为的中点，
因为，，
所以，
又因平面，所以平面，
又平面，所以平面平面，
作，垂足为，
因为平面平面，平面平面，平面，
所以平面，
则与平面所成的角为，
在中，，所以，
即直线与平面所成角的正弦值为，故D错误.
故选：AC.
（四）
向量法证明平行、垂直
(1)利用向量法证明平行、垂直关系，关键是建立恰当的坐标系(尽可能利用垂直条件，准确写出相关点的坐标，进而用向量表示涉及到直线、平面的要素)．
(2)向量证明的核心是利用向量的数量积或数乘向量，但向量证明仍然离不开立体几何的有关定理．
题型4：向量法证明平行
4-1．（2024高三·全国·专题练习）四棱锥中，底面为矩形，平面，为的中点，证明：平面.
【答案】证明见解析.
【分析】连结BD交AC于点O，连结EO，证明EO为的中位线，则EO//PB，即可推出线面平行.
【详解】连结BD交AC于点O，连结EO，
因为ABCD为矩形，所以O为BD的中点，
又E为的PD的中点，所以EO为的中位线，则EO//PB，
因为EO平面AEC，PB平面AEC，所以PB//平面AEC.
【点睛】本题考查线面平行的证明，属于基础题.
4-2．（2024高二下·江苏·课后作业）如图所示，平面PAD⊥平面ABCD，四边形ABCD为正方形，△PAD是直角三角形，且PA＝AD＝2，E，F，G分别是线段PA，PD，CD的中点，求证：平面EFG∥平面PBC．
【答案】证明过程见详解
【分析】根据题意得到AB，AP，AD两两垂直，从而以A为坐标原点，AB，AD，AP所在直线分别为x轴，y轴，z轴，建立空间直角坐标系，并确定A，B，C，D，P，E，F，G的坐标，求得，，，，从而即可确定平面EFG的法向量，平面PBC的法向量，进而即可证明平面EFG∥平面PBC．
【详解】因为平面PAD⊥平面ABCD，四边形ABCD为正方形，△PAD是直角三角形，
所以AB，AP，AD两两垂直，
以A为坐标原点，AB，AD，AP所在直线分别为x轴，y轴，z轴，建立空间直角坐标系，
则A(0，0，0)，B(2，0，0)，C(2，2，0)，D(0，2，0)，P(0，0，2)，E(0，0，1)，F(0，1，1)，G(1，2，0)．
所以，，，，
设是平面EFG的法向量，
则，，即，得，
令，则，，所以，
设是平面PBC的法向量，
由，，即，得，
令，则，，所以，
所以，所以平面EFG∥平面PBC．
4-3．（2024高二·全国·课后作业）如图，在直四棱柱中，底面为等腰梯形，，，，，是棱的中点．求证：平面平面.
【答案】证明见解析
【分析】建立空间直角坐标系，利用向量法分别证明，，即，，再利用面面平行的判定定理即可得证.
【详解】因为，是棱的中点，
所以，所以为正三角形.
因为为等腰梯形，，
所以.
取的中点，连接，
则，所以.
以为原点，所在直线分别为轴，轴，轴建立空间直角坐标系，
则，
所以，，，，
所以，，
又不重合，不重合，
所以，，
因为平面， 平面，
所以平面，平面，
又，平面，
所以平面平面
4-4．（2024高二·全国·专题练习）如图，在四棱锥中，底面为矩形，平面平面，，，，，分别是，的中点. 求证：平面.

【答案】证明见解析
【分析】建立空间直角坐标系，利用向量法来证得平面
【详解】由题意，
在矩形中，，，，
，分别是，的中点，
∴，，
在四棱锥中，面平面，
面面，，平面， ∴面，
面，∴，
取中点，连接，
∵，
∴，所以四边形是平行四边形，∴，
∵，∴，
∵面，面，
∴面，∵平面，
∴
以、、为、、轴建立空间直角坐标系如下图所示，
∴，
∴，面的一个法向量为，
∵，平面，
∴平面.

4-5．（2024高二上·全国·课后作业）如图所示，在四棱锥中，底面为矩形，平面，为的中点，为的中点，，求证：．

【答案】证明见解析
【分析】证法一：以为坐标原点，所在直线分别为轴､轴､轴建立空间直角坐标系，求出的坐标，利用空间向量共线的坐标表示可得答案；
证法二：由空间向量的线性表示可得答案.
【详解】证法一：由题意知，直线两两垂直，
以为坐标原点，所在直线分别为轴､轴､轴建立空间直角坐标系，如图所示，
则，
所以，
所以，又，故．
证法二：由题意可得
，
又，所以．

题型5：向量法证明垂直
5-1．（2024高三·全国·专题练习）如图，在四棱锥中，平面，，，，.为的中点，点在上，且.
求证：平面平面.
【答案】证明见解析
【分析】如图，以为原点，分别以，为轴，轴，过作平行线为轴，建立空间直角坐标系，求出两平面的法向量，利用空间向量证明即可.
【详解】证明：如图，以为原点，分别以，为轴，轴，过作平行线为轴，建立空间直角坐标系，
则，，，，，，
所以，，因为，所以，
所以，即，
所以，，
设平面的法向量为，则，
令，则，所以，
平面的法向量为，则，
令，则，所以，
所以，
所以，
所以平面平面.
5-2．（2024高二·全国·专题练习）已知在直三棱柱中，其中为的中点，点是上靠近的四等分点，与底面所成角的余弦值为．

求证：平面平面.
【答案】证明见解析
【分析】根据与底面所成角的余弦值为得到是边长为的等边三角形，然后利用空间向量的方法证明平面平面即可.
【详解】
取的中点，连，
因为为的中点，所以，，
所以四边形为平行四边形，所以，
因为与底面所成角的余弦值为，所以与底面所成角的余弦值为，
因为三棱柱为直三棱柱，所以平面，所以是与底面所成角，所以，所以，所以，
又，所以是边长为的等边三角形，
取的中点，的中点，连，则，，平面，
以为原点，的方向为轴建立空间直角坐标系：
则，，，，，，，，，
，，，，
设平面的一个法向量为，平面的一个法向量为，
则，得，令，得，，
，令，得，，，
因为，所以，
所以平面平面.
5-3．（2024高三·全国·专题练习）如图，已知直三棱柱为的中点，为侧棱上一点，且，三棱柱的体积为32．过点作，垂足为点，求证：平面；
【答案】证明见解析
【分析】先根据三棱柱的体积为32，求出，再由题意可得两两垂直，所以以为原点，所在的直线分别为轴建立空间直角坐标系，利用空间向量证明即可.
【详解】由直三棱柱，得平面，又，
可得三棱柱的体积，得．
因为三棱柱为直三棱柱，所以，
因为，所以两两垂直，
所以以为原点，所在的直线分别为轴建立空间直角坐标系，如图所示，
则，
则．设，则，
故．
因为，所以，
所以，解得，即．
所以，
所以，
.
所以．
又因为平面ACQ，平面ACQ，，
所以平面．
5-4．（2024高三·全国·专题练习）如图，在四棱锥中，底面，底面是边长为2的正方形，，，分别是，的中点．求证：平面；
【答案】证明见解析
【分析】由题意可得两两垂直，所以以为原点，所在直线为轴，轴，轴，建立如图所示空间直角坐标系，再利用空间向量证明即可.
【详解】证明：因为底面，底面，且底面是边长为2的正方形，
所以两两垂直，
所以以为原点，所在直线为轴，轴，轴，建立如图所示空间直角坐标系，

则，，，，，，
所以，，，
设平面的法向量，
则，取可得，
所以平面的一个法向量为，
因为，所以平面.
5-5．（2024高二上·山西太原·期中）如图，在平行六面体中，.
(1)求的长；
(2)求证：.
【答案】(1);
(2)证明见解析.
【分析】（1）利用，即可求出答案.
（2）利用，即可证明答案.
【详解】（1）
则.
（2）证明：
故.