2022-2023学年五年级数学上册典型例题系列之期末题型专项练习五：高频易错作图10题（解析版）北师大版

这是一份2022-2023学年五年级数学上册典型例题系列之期末题型专项练习五：高频易错作图10题（解析版）北师大版，共10页。试卷主要包含了作图题等内容，欢迎下载使用。
五、作图题。
1．（2022·广东惠州·五年级期末）画出图形①的另一半，使它成为一个轴对称图形。
【答案】见详解
【分析】根据轴对称图形的特征，对称点到对称轴的距离相等，对称点的连线垂直于对称轴，在对称轴的右边画出图形①的关键对称点，依次连接即可画出图形①的另一半，使它成为一个轴对称图形。
【详解】
【点睛】这道题主要考查：求作一个几何图形关于某条直线对称的图形，可以转化为求作这个图形上的特征点关于这条直线对称的点，然后依次连接各对称点即可。
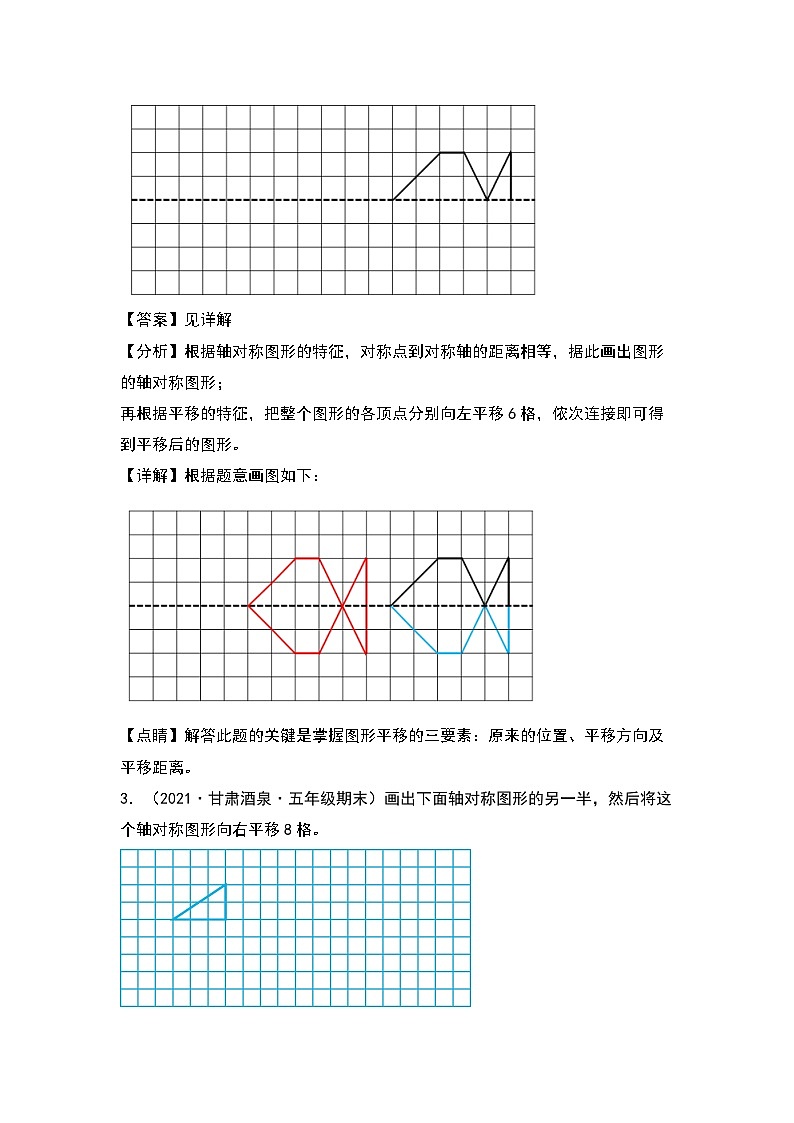
2．（2021·甘肃酒泉·五年级期末）以虚线为对称轴，画出下图的轴对称图形，再将整个图形向左平移6格。
【答案】见详解
【分析】根据轴对称图形的特征，对称点到对称轴的距离相等，据此画出图形的轴对称图形；
再根据平移的特征，把整个图形的各顶点分别向左平移6格，依次连接即可得到平移后的图形。
【详解】根据题意画图如下：
【点睛】解答此题的关键是掌握图形平移的三要素：原来的位置、平移方向及平移距离。
3．（2021·甘肃酒泉·五年级期末）画出下面轴对称图形的另一半，然后将这个轴对称图形向右平移8格。
【答案】见详解
【分析】根据轴对称图形的特征，对称点到对称轴的距离相等，对称点的连线垂直于对称轴，在对称轴的右边画出左半图的关键对称点，依次连接即可画出下面轴对称图形的另一半；根据平移的特征，把这个轴对称图形的各顶点分别向右平移8格，依次连接即可得到平移后的图形。
【详解】如图：
【点睛】作平移后的图形、作轴对称图形，对应点（对称点）位置的确定是关键。
4．（2022·广东湛江·六年级期末）如图中每格都代表1平方厘米，请你尽量利用方格纸中的点和线，分别画出面积是6平方厘米的平行四边形、三角形、梯形。
【答案】见详解
【分析】先依据面积是6平方厘米，分别确定出平行四边形的底和高、三角形的底和高以及梯形的上底、下底与高的值，进而可以作出符合要求的图。
【详解】因为面积是6平方厘米，则平行四边形的底和高分别为3厘米和2厘米；
三角形的底和高分别为4厘米和3厘米；
梯形的上底、下底与高分别为2厘米、4厘米和2厘米；
于是所画图形如下所示：
（答案不唯一）
【点睛】解答此题的关键是：先依据面积确定出所需要的线段的长度，进而作出符合要求的图。
5．（2022·广东惠州·五年级期末）画出图形②向右平移5格后的图形，再画出选续向上平移3格后的图形。
【答案】见详解
【分析】根据平移图形的特征，把图形②的四个顶点分别向右平移5格，再顺次连接各点，即可得到图形②向右平移5格的图形③；
同理，把图形③的四个顶点分别向上平移3格，再顺次连接各点，即可得到图形③向上平移3格的图形④。
【详解】如图：
。
【点睛】本题考查了作平移后的图形，以上知识需要熟练掌握并且灵活运用，尤其需要能结合知识准确画图。
6．（2022·广东深圳·五年级期末）根据下面图形中标出的底，画出底边上的高。
【答案】见详解
【分析】从平行四边形一条边上的一点到它对边的垂直线段叫做平行四边形的高；
从三角形的一个顶点到它的对边作一条垂线，顶点和垂足之间的线段叫做三角形的高；据此画图。
【详解】由分析作图如下：
【点睛】本题考查三角形、平行四边形高的画法，注意垂足所在的边叫做底。
7．（2021·陕西商洛·五年级期末）在如图的方格中画图（每小格面积是1平方厘米）请在图中画出面积是10平方厘米的平行四边形和5平方厘米的三角形。
【答案】图见详解
【分析】根据平行四边形面积公式：S＝a×h，三角形面积公式：S＝ah÷2，将数值代入公式，据此画图即可。
【详解】由分析可得：
要画的平行四边形面积为10平方厘米和三角形面积为5平方厘米，
当平行四边形底为5厘米、高为2厘米时，面积为：
5×2＝10（平方厘米）
当三角形底为5厘米，高为2厘米时，面积为：
5×2÷2
＝10÷2
＝5（平方厘米）
所以可以画一个底为5厘米、高为2厘米的平行四边形，其面积是10平方厘米，画一个底为5厘米、高为2厘米的三角形，其面积是5平方厘米。（图形画法不唯一）
画图如下：
【点睛】本题考查了平行四边形四边形面积、三角形面积的计算，同时要求学生会画指定面积的平行四边形和三角形。
8．（2022·陕西汉中·五年级期末）按要求画一画。
（1）以虚线为对称轴，画出图形①的另一半。
（2）将图形②先向右平移8格，再向上平移3格。
（3）如果每个小方格的边长表示1厘米，画出一个与图形②面积相等的平行四边形。
【答案】（1）（2）（3）见详解
【分析】（1）根据轴对称图形的特征，对称点到对称轴的距离相等，对称点的连线垂直于对称轴，在对称轴（虚线）的右边画出图①的左图的关键对称点，依次连接即可；
（2）根据平移的特征，把图②的各顶点分别向右平移8格，再向上平移3个，依次连接即可得到平移后的图形；
（3）图②的上底是2厘米，下底是4厘米，高是3厘米，根据梯形的面积公式：面积＝（上底＋下底）×高÷2，代入数据，求出这个梯形的面积，（2＋4）×3÷2＝9平方厘米，根据平行四边形面积公式：面积＝底×高，底是3厘米，高是3厘米，画出平行四边形（答案不唯一）。
【详解】（1）（2）见下图；
（3）（2＋4）×3÷2
＝6×3÷2
＝18÷2
＝9（平方厘米）
平行四边形的底是3厘米，高是3厘米。
【点睛】本题考查作轴对称图形，作平移后的特征，画平行四边形，以及梯形面积公式、平行四边形面积公式的应用。
9．（2022·陕西西安·五年级期末）涂色表示下面各分数。
【答案】见详解
【分析】根据分数的意义可知：把一个整体平均分成若干份，取其中的几份就是几分之几，由于第一个图形是9个小格，分数是，相当于把9个小格平均分成3份，取1份，即1份涂3个小格；第二个图形是涂色，由于表示1＋，即把一个整体涂色，之后再把第二个整体平均分成4份，涂1份即可。
【详解】由分析可知：如下图所示
【点睛】本题主要考查分数的意义以及假分数的认识，熟练掌握分数的意义并灵活运用。
10．（2022·广东深圳·六年级期末）（如图）点子图中，每两个点子之间的距离是1厘米，画出底为3厘米，高为2厘米的直角三角形、钝角三角形和平行四边形各一个。
【答案】见解析
【分析】根据三角形的特征和平行四边形的特征，按照要求画出这个三角形和平行四边形即可。
【详解】作图如下：
【点睛】此题考查的目的是理解掌握直角三角形、钝角三角形、平行四边形的特征。