2023-2024学年湖北省随州市曾都区七年级（上）期中数学试卷

这是一份2023-2024学年湖北省随州市曾都区七年级（上）期中数学试卷，共18页。
A．1B．C．﹣D．﹣2
2．（2分）下列各数：﹣π，﹣|﹣2|，2022，﹣1.010010001，﹣3.5中，负数的个数有（ ）
A．2个B．3个C．4个D．5个
3．（2分）下列各式中，不相等的是（ ）
A．（﹣3）2和﹣32B．（﹣3）2和32
C．（﹣2）3和﹣23D．|﹣2|3和|﹣23|
4．（2分）手机支付给生活带来便捷，如图是王老师某日微信账单的收支明细（正数表示收入，负数表示支出，单位：元），王老师当天微信收支的最终结果是（ ）
A．收入14元B．支出3元C．支出18元D．支出10元
5．（2分）下列说法中错误的有（ ）
①﹣1与0之间没有负数；
②如果|x|＝2，那么x的值是2；
③两个数比较大小绝对值大的反而小；
④如果x＝﹣x，那么x＝0；
⑤如果|x|＝x，那么x＝0；
⑥如果两个数的和为0，那么这两个数互为相反数．
A．2个B．3个C．4个D．5个
6．（2分）下列结论中正确的是（ ）
A．单项式的系数是，次数是4
B．单项式m的次数是1，没有系数
C．多项式2x2+xy2+3是二次三项式
D．2x+y，﹣a2b，0它们都是整式
7．（2分）用四舍五入法，分别按要求取2.1704的近似值，下列结果错误的是（ ）
A．2.2（精确到0.1）B．2.17（精确到0.01）
C．2（精确到个位）D．2.17（精确到千分位）
8．（2分）下列关于方程的变形，正确的是（ ）
A．由3+x＝7，得x＝7+3
B．由5x＝﹣4，得x＝﹣
C．由x＝3得x＝3×
D．由﹣＝1，得﹣（x﹣2）＝4
9．（2分）若xy＝x﹣2，则2xy+3x﹣5xy+10的值为（ ）
A．4B．10C．16D．20
10．（2分）任何一个无限循环小数都可以写成分数的形式，应该怎样写呢？我们以无限循环小数0.为例进行说明：设0.，由0.可知，10x＝7.777⋯，所以10x﹣x＝7，解方程，得x＝．于是，得0.，将0.写成分数的形式是（ ）
A．B．C．D．
二．填空题（共14小题，每小题2分，共28分）
11．（2分）若代数式3a+1的值与代数式3（a﹣1）的值互为相反数，则a＝ ．
12．（2分）将数据15.7万用科学记数法表示为 ．
13．（2分）大于﹣4.6而小于2.3的整数共有 个．
14．（2分）多项式是关于x，y的三次二项式，则m的值是 ．
15．（2分）近似数1.70的准确值a的取值范围是 ．
16．（2分）若单项式7x1﹣my2n和﹣4x3y4是同类项，则mn的值为 ．
17．（2分）若方程（m2﹣1）x2﹣（m﹣1）x+2＝0是关于x的一元一次方程，则代数式|m﹣1|的值为 ．
18．（2分）当x＝2023时，代数式ax3+bx+5的值为1，则当x＝﹣2023时，ax3+bx+5的值为 ．
19．（2分）已知|a|＝3，|b﹣1|＝5，且a＞b，则a+b的值为 ．
20．（2分）已知a、b、c在数轴上位置如图所示，则|a+b|+|a+c|﹣|b﹣c|＝ ．
21．（2分）已知a，b为有理数，下列结论：①若a＞b，则＜；②若a+b＝0，则＝﹣1；③若a3+b3＝0，则a+b＝0；④|a|＝|﹣2|，则a＝﹣2；⑤若ab＞0，则|a+b|＝|a|+|b|；⑥a2≥a．其中正确的为 ．（填序号）
22．（2分）定义一个运算f（a，b）＝，已知|a﹣2|＝1，b＝2，那么f（a，b）＝ ．
23．（2分）若|m﹣2023|与|2022﹣n|互为相反数，则的值为 ．
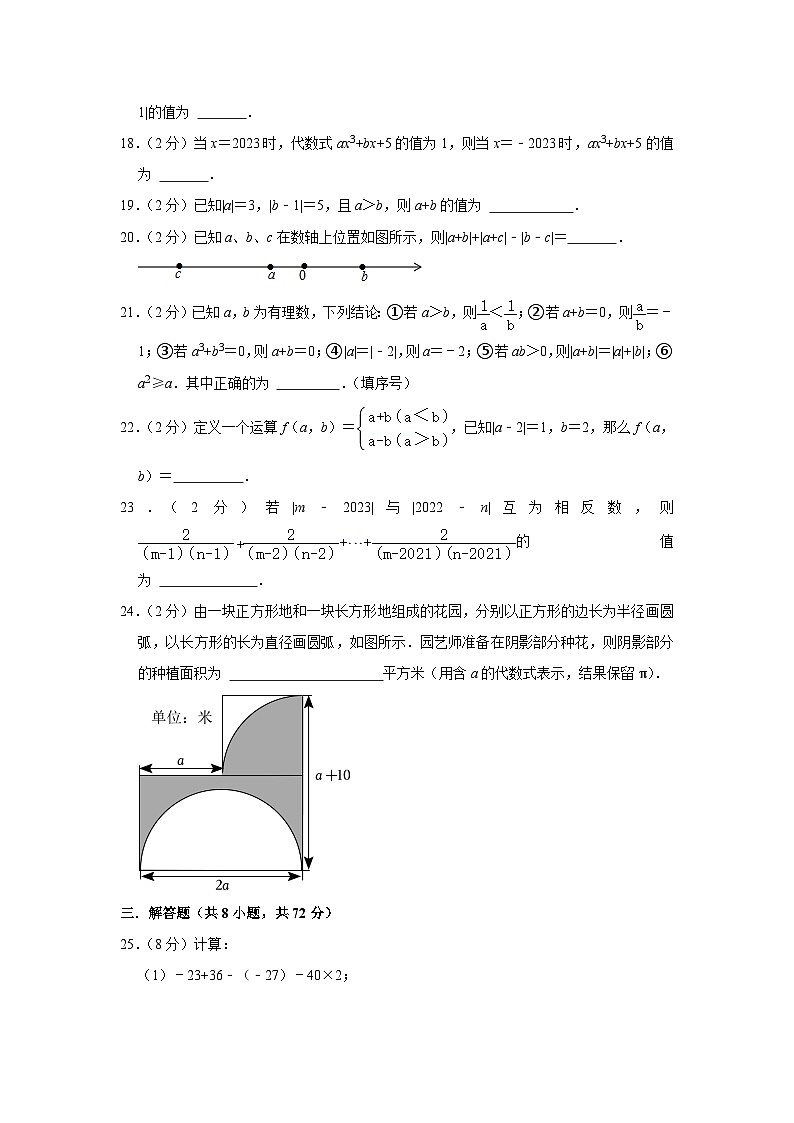
24．（2分）由一块正方形地和一块长方形地组成的花园，分别以正方形的边长为半径画圆弧，以长方形的长为直径画圆弧，如图所示．园艺师准备在阴影部分种花，则阴影部分的种植面积为 平方米（用含a的代数式表示，结果保留π）．
三．解答题（共8小题，共72分）
25．（8分）计算：
（1）﹣23+36﹣（﹣27）﹣40×2；
（2）﹣14﹣（1﹣0.5）××[3﹣（﹣3）2]．
26．（8分）先化简，再求值：2a2b﹣[2ab2﹣2（ab﹣a2b﹣1）+ab]+2ab2+2，其中a＝﹣3，b＝2．
27．（8分）解方程：
（1）5x+3＝﹣2x﹣11；
（2）3（y﹣7）﹣5（4﹣y）＝15．
28．（9分）乐乐在妈妈的监督下进行了7次跳绳检测，检测他一分钟跳绳的个数，并把每次的个数都与前一次进行比较，超出的部分记为“+”，不足的部分记为“﹣”．下表记录了他第2次到第7次的检测结果．
（1）若乐乐第1次的检测成绩为m个．请直接写出：
①第4次检测成绩的个数（用m表示）；
②第2次到第6次的检测中成绩超过m个的次数．
（2）若乐乐第1次的检测成绩为100个，第7次的检测成绩为106个．
①求表中n的值；
②乐乐妈妈为了鼓励乐乐，每跳绳一个奖励1颗小星星，并从第2次开始，与前一次进行比较，每超过一个再额外奖励2颗小星星，求乐乐这7次检测共能得到多少颗小星星．
29．（8分）如图为武汉市地铁2号线地图的一部分，学生小王某天参加志愿者服务活动，从洪山广场站出发，到从A站出站时，本次志愿者服务活动结束．如果规定向东为正，向西为负，当天的乘车站数按先后顺序依次记录如下：
+4，﹣3，+6，﹣8，+5，﹣2，﹣3，+1．
（1）请通过计算说明A站是哪一站？
（2）若相邻两站之间的平均距离为1.2千米，求这次小王志愿服务期间乘坐地铁行进的总路程约是多少千米？
30．（12分）（1）已知代数式A＝2x2﹣2x﹣1，B＝﹣x2+xy+1，M＝4A﹣（3A﹣2B）．当（x+1）2+|y﹣2|＝0时，求代数式M的值．
（2）若代数式（2x2+ax﹣y+6）﹣（2bx2﹣3x+5y﹣1）的值与字母x的取值无关，求代数式2a﹣b的值．
31．（7分）已知a是最大的负整数，b是﹣5的相反数，且a、b分别是点A、B、在数轴上对应的数．
（1）求a、b的值，并在数轴上标出点A、B．
（2）若动点P从点A出发沿数轴正方向运动，动点Q同时从点B出发也沿数轴正方向运动，点P的速度是每秒3个单位长度，点Q的速度是每秒1个单位长度，若运动t秒后，点P可以追上点Q，求t的值？
32．（12分）观察下面有一定规律的三组数：
（1）﹣2，4，﹣6，8，﹣10，…；
（2）﹣5，1，﹣9，5，﹣13，…；
（3），﹣1，，﹣2，，…；
解答下列问题：
（1）每组的第7个数分别是 ， ， ；
（2）第二组和第三组的第n个数分别是 ；（用含n的式子来表示）
（3）取每组的第k个数，若这三个数的和为172，求k的值．
2023-2024学年湖北省随州市曾都区七年级（上）期中数学试卷
参考答案与试题解析
一．选择题（共10小题，每小题2分，共20分）
1．【分析】根据倒数的定义即可求解．
【解答】解：﹣2的倒数是﹣．
故选：C．
【点评】本题考查了倒数的概念及性质，掌握倒数的定义：若两个数的乘积是1，我们就称这两个数互为倒数是关键．
2．【分析】通常情况下，把数分为正数、负数和0，负数前面带“﹣”号，正数前面加“+”号或没有任何符号，0既不是负数，也不是正数．
【解答】解：﹣|﹣2|＝﹣2，
在实数﹣π，﹣|﹣2|，2022，﹣1.010010001，﹣3.5中，负数有﹣π，﹣|﹣2|，﹣1.010010001，﹣3.5，共4个．
故选：C．
【点评】此题考查相反数、绝对值以及负数的意义，掌握正负数的意义是解决问题的关键．
3．【分析】根据有理数的乘方、绝对值和负整数指数幂的知识点进行解答，即可判断．
【解答】解：A、（﹣3）2＝9，﹣32＝﹣9，故（﹣3）2≠﹣32；
B、（﹣3）2＝9，32＝9，故（﹣3）2＝32；
C、（﹣2）3＝﹣8，﹣23＝﹣8，则（﹣2）3＝﹣23；
D、|﹣2|3＝23＝8，|﹣23|＝|﹣8|＝8，则|﹣2|3＝|﹣23|．
故选：A．
【点评】此题确定底数是关键，要特别注意﹣32和（﹣3）2的区别．
4．【分析】根据正数和负数的实际意义列式计算即可．
【解答】解：14﹣8﹣9＝﹣3（元），
即王老师当天微信收支的最终结果是支出3元，
故选：B．
【点评】本题考查正数和负数，结合已知条件列得正确的算式是解题的关键．
5．【分析】根据相反数、绝对值，有理数的大小比较，理解相反数、绝对值的定义逐个进行判断即可．
【解答】解：①﹣1与0之间有无数个负数，因此①不正确；
②如果|x|＝2，那么x的值是±2，因此②不正确；
③两个负数比较大小，绝对值大的反而小，因此③不正确；
④如果x＝﹣x，那么x＝0，因此④正确；
⑤如果|x|＝x，那么x≥0，因此⑤不正确；
⑥如果两个数的和为0，那么这两个数互为相反数，因此⑥正确
综上所述，不正确的有①②③⑤，共4个．
故选：C．
【点评】本题考查相反数、绝对值，有理数的大小比较，理解相反数、绝对值的定义，掌握有理数大小是比较方法是正确解答的前提．
6．【分析】单项式中的数字因数叫做单项式的系数，一个单项式中所有字母的指数的和叫做单项式的次数；多项式中次数最高的项的次数叫做多项式的次数，多项式中单项式的个数就是多项式的项数；单项式和多项式统称为整式．
【解答】解：A、单项式的系数是，次数是3，故A不符合题意；
B、单项式m的次数是1，系数是1，故B不符合题意；
C、多项式2x2+xy2+3是三次三项式，故B不符合题意；
D、2x+y，﹣a2b，0它们都是整式，正确，故D符合题意，
故选：D．
【点评】本题考查多项式，单项式的有关概念，关键是掌握整式的概念；单项式的系数，次数的概念；多项式的次数，项的概念．
7．【分析】按要求分别取近似值即可得出答案．
【解答】解：2.1704精确到0.1为2.2，2.1704精确到0.01为2.17，
2.1704精确到个位为2，2.1704精确到千分位为2.170，
故选：D．
【点评】本题主要考查近似数，近似数与精确数的接近程度，可以用精确度表示．一般有，精确到哪一位，保留几个有效数字等说法．
8．【分析】根据解一元一次方程的步骤逐一判断即可．
【解答】解：A、由3+x＝7，得x＝7﹣3，变形错误，不符合题意；
B、由5x＝﹣4，得x＝﹣，变形错误，不符合题意；
C、由x＝3得x＝3×，变形错误，不符合题意；
D、由﹣＝1，得﹣（x﹣2）＝4，变形正确，符合题意；
故选：D．
【点评】本题主要考查了解一元一次方程，熟知解一元一次方程的步骤是解题的关键．
9．【分析】先根据合并同类型法则进行化简，然后将xy﹣x＝﹣2代入原式即可求出答案．
【解答】解：原式＝﹣3xy+3x+10
＝﹣3（xy﹣x）+10
当xy﹣x＝﹣2时，
原式＝﹣3×（﹣2）+10
＝6+10
＝16，
故选：C．
【点评】本题考查整式的加减运算，解题的关键是熟练运用整式的加减运算，本题属于基础题型．
10．【分析】根据题意可得，设，则100x﹣x＝36，求解即可．
【解答】解：设，由题意可得100x﹣x＝36，
解得，即．
故选：C．
【点评】此题考查了一元一次方程的应用，解题的关键是理解题意，正确列出一元一次方程．
二．填空题（共14小题，每小题2分，共28分）
11．【分析】根据互为相反数的两个数相加为零列出一元一次方程，解这个方程即可．
【解答】解：根据题意得：3a+1+3（a﹣1）＝0，
去括号得：3a+1+3a﹣3＝0，
移项得：3+3a＝3﹣1，
合并同类项得：6a＝2，
系数化为1得：．
故答案为：．
【点评】本题主要考查了相反数的知识、一元一次方程的知识，难度不大，认真计算即可．
12．【分析】科学记数法的表现形式为a×10n的形式，其中1≤|a|＜10，n为整数，确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同，当原数绝对值大于等于10时，n是正整数，当原数绝对值小于1时，n是负整数；由此进行求解即可得到答案．
【解答】解：15.7万＝157000＝1.57×105．
故答案为：1.57×105．
【点评】本题主要考查了科学记数法的表示方法，熟练掌握科学记数法的表示方法是解题的关键．
13．【分析】有理数大小比较的法则：正数＞0＞负数，两个负数比较大小，绝对值大的其值反而小，据此判断即可．
【解答】解：根据有理数比较大小的方法，可得：
大于﹣4.6而小于2.3的整数有：﹣4、﹣3、﹣2、﹣1、0、1、2，共7个．
故答案为：7．
【点评】此题主要考查了有理数大小比较，解答此题的关键是掌握有理数大小比较法则．
14．【分析】直接利用三次二式的定义得出关于m的等式进而得出答案．
【解答】解：∵多项式是关于x，y的三次二项式，
∴|m|+2＝3，m+1＝0，
解得：m＝﹣1．
故答案为：﹣1．
【点评】此题主要考查了多项式，正确把握多项式的定义是解题关键．
15．【分析】根据近似数通常用四舍五入的方法得到，精确到哪一位，只需对下一位数字进行四舍五入，即可得出答案．
【解答】解：根据取近似数的方法可得：
1.70可以由大于或等于1.695的数，9后面的一位数字，满5进1得到；
或由小于1.705的数，舍去0后的数字得到，
则近似数1.70所表示的准确数a的范围是1.695≤a＜1.705．
故答案为：1.695≤a＜1.705．
【点评】本题考查了近似数与有效数字：近似数与精确数的接近程度，可以用精确度表示．一般有，精确到哪一位，保留几个有效数字等说法．从一个数的左边第一个不是0的数字起到末位数字止，所有的数字都是这个数的有效数字．
16．【分析】根据同类项的概念分别求出m、n，根据有理数的乘方法则计算，得到答案．
【解答】解：∵单项式7x1﹣my2n和﹣4x3y4是同类项，
∴1﹣m＝3，2n＝4，
解得：m＝﹣2，n＝2，
∴mn＝（﹣2）2＝4，
故答案为：4．
【点评】本题考查的是同类项，所含字母相同，并且相同字母的指数也相同，这样的项叫做同类项．
17．【分析】利用一元一次方程的定义，可列出关于m的一元二次方程及一元一次不等式，解之可得出m的值，再将其代入|m﹣1|中，即可求出结论．
【解答】解：∵方程（m2﹣1）x2﹣（m﹣1）x+2＝0是关于x的一元一次方程，
∴，
解得：m＝﹣1，
∴|m﹣1|＝|﹣1﹣1|＝2．
故答案为：2．
【点评】本题考查了一元一次方程的定义以及绝对值，牢记“只含有一个未知数（元），且未知数的次数是1，这样的方程叫一元一次方程”是解题的关键．
18．【分析】将x＝2023代入求得关于a，b的代数式的值，再利用整体代入的方法解答即可．
【解答】解：∵当x＝2023时，代数式ax3+bx+5的值为1，
∴20233a+2023b+5＝1．
∴20233a+2023b＝﹣4，
∴当x＝﹣2023时，
ax3+bx+5
＝（﹣2023）3a﹣2023b+5
＝﹣20233a﹣2023b+5
＝﹣（20233a+2023b）+5
＝﹣（﹣4）+5
＝4+5
＝9．
故答案为：9．
【点评】本题主要考查了求代数式的值，利用整体代入的方法解答是解题的关键．
19．【分析】根据绝对值的性质求出a与b的值，再代入进行计算即可．
【解答】解：∵|a|＝3，|b﹣1|＝5，
∴a＝±3，b＝6或﹣4，
∵a＞b，
∴a＝3，b＝﹣4或a＝﹣3，b＝﹣4，
则a+b＝﹣1或﹣7．
故答案为：﹣1或﹣7．
【点评】本题考查有理数的加法和绝对值，掌握绝对值的性质是解题的关键．
20．【分析】通过数轴判断a，c，b的相对大小，可知c＜a＜0＜b，且|c|＞|b|＞|a|，从而确定绝对值里代数式的值的符号，再去掉绝对值，最后实现化简．
【解答】解：由数轴可知c＜a＜0＜b，且|c|＞|b|＞|a|，
∴a+b＞0，a+c＜0，b﹣c＞0
∴|a+b|+|a+c|﹣|b﹣c|＝（a+b）﹣（a+c）﹣（b﹣c）＝0
故答案为0．
【点评】本题考查的是利用数轴比较数的大小，并进行化简，利用数轴判断绝对值内代数式的符号是解题关键．
21．【分析】①举反例说明；②举反例说明；③根据“（﹣a）3＝﹣a3”判断求解；④根据绝对值的定义判断即可；⑤根据同号的和的绝对值等于绝对值的和；⑥举反例说明．
【解答】解：①∵1＞﹣2，
∴1＞﹣，故①是错误的；
②当a＝b＝0时，没有意义，故②是错误的；
③若a3+b3＝0，则a＝﹣b，即a+b＝0，故③是正确的；
④∵|a|＝|﹣2|，则a＝±2，故⑤是错误的；
⑤若ab＞0，则a和b同号，
所以|a+b|＝|a|+|b|，故⑤是正确的；
⑥例如：0.52＝0.25，0.25＜0.5，故⑥是错误的．
故答案为：③⑤．
【点评】本题考查了有理数的运算及绝对值，掌握数学的基本知识是解题的关键．
22．【分析】先根据|a﹣2|＝1可得a＝1或3，再根据题意进行分类讨论即可求解．
【解答】解：∵|a﹣2|＝1，
∴a﹣2＝1或a﹣2＝﹣1，
∴a＝3或1，
∵b＝2，
∴①当a＝3，b＝2时，
f（a，b）＝a﹣b
＝3﹣2
＝1；
②当a＝1，b＝2时，
f（a，b）＝a+b
＝1+2
＝3；
综上所述：f（a，b）＝1或3，
故答案为：1或3．
【点评】本题主要考查了绝对值和有理数的运算，理解题意掌握绝对值的性质及有理数的加减法法则是解题的关键，运用了分类讨论的数学思想．
23．【分析】先根据相反数的定义结合非负数的性质求出m，n，再代入后抵消法计算即可求解．
【解答】解：∵|m﹣2023|与|2022﹣n|互为相反数，
∴|m﹣2023|+|2022﹣n|＝0，
∴m﹣2023＝0，2022﹣n＝0，
解得m＝2023，n＝2022，
∴
＝++……+
＝2×（﹣+﹣+……+1﹣）
＝2×（﹣+1）
＝2×
＝．
故答案为：．
【点评】本题考查了非负数的性质：几个非负数的和为0时，这几个非负数都为0．
24．【分析】首先依题意求出正方形的边长为a米，进而得长方形的宽为10米，然后根据正方形内阴影部分的面积是四分之一圆的面积，长方形内阴影部分的面积＝长方形的面积﹣半圆的面积即可得出答案．
【解答】解：如图所示：
依题意得：四边形ABCD为正方形，四边形CEFG为长方形，
∴CD＝AB＝BC＝AD，CE＝FG＝2a米，EF＝CG，
∵DE＝a米，
∴CE＝DE+CD＝a+CD，
∴a+CD＝2a，
∴CD＝a 米，
∴正方形ABCD的边长为a米，即BC＝a米，
∵GB＝BC+CG＝a+10，
∴CG＝10，
∴S阴影＝πa2+10×2a﹣πa2＝（20a﹣πa2）平方米．
故答案为：（20a﹣πa2）．
【点评】此题主要考查了列代数式，熟练掌握圆的面积公式，长方形的面积公式是解答问题的关键．
三．解答题（共8小题，共72分）
25．【分析】（1）根据有理数混合运算的运算顺序进行计算即可；
（2）根据有理数混合运算的运算顺序进行计算即可．
【解答】解：（1）﹣23+36﹣（﹣27）﹣40×2
＝﹣23+36+27﹣80
＝﹣40；
（2）﹣14﹣（1﹣0.5）××[3﹣（﹣3）2]
＝﹣1﹣×（3﹣9）
＝﹣1﹣（﹣6）
＝﹣1+1
＝0．
【点评】本题考查了有理数的混合运算，关键在计算乘方时注意结果的正负．
26．【分析】先去括号，再合并同类项得到最简结果，最后将a，b的值代入计算即可．
【解答】解：原式＝2a2b﹣（2ab2﹣ab+3a2b+2+ab）+2ab2+2
＝2a2b﹣2ab2+ab﹣3a2b﹣2﹣ab+2ab2+2
＝﹣a2b，
当a＝﹣3，b＝2时，原式＝﹣（﹣3）2×2＝﹣18．
【点评】本题考查整式的加减﹣化简求值，熟练掌握运算法则是解答本题的关键．
27．【分析】（1）方程移项，合并同类项，把x系数化为1，即可求出解；
（2）方程去括号，移项，合并同类项，把y系数化为1，即可求出解．
【解答】解：（1）移项得：5x+2x＝﹣11﹣3，
合并同类项得：7x＝﹣14，
系数化为1得：x＝﹣2；
（2）去括号得，3y﹣21﹣20+5y＝15，
移项得：3y+5y＝15+21+20，
合并同类项得：8y＝56
系数化为1得：y＝7．
【点评】此题考查了解一元一次方程，熟练掌握一元一次方程的解法是解本题的关键．
28．【分析】（1）①根据表格即可求解；
②根据表格可得第2次到第6次的检测中成绩超过m个的次数．
（2）①根据乐乐第1次的检测成绩为100个，第7次的检测成绩为106个可求表中n的值；
②根据每跳绳一个奖励1颗小星星，并从第2次开始，与前一次进行比较，每超过一个再额外奖励2颗小星星即可求解．
【解答】解：（1）①第4次检测成绩的个数（用m表示）为：m+1﹣8+5＝m﹣2；
②第2次到第6次的检测中成绩依次为m+1，m﹣7，m﹣2，m+2，m+7，
故第2次到第6次的检测中成绩超过m个的次数是3次；
（2）①依题意有：n+7＝106﹣100，
解得n＝﹣1．
故表中n的值为﹣1；
②（100+101+93+98+102+107+106）+（1+5+4+5）×2
＝707+15×2
＝707+30
＝737（颗）．
故乐乐这7次检测共能得到737颗小星星．
【点评】本题考查了列代数式，正数与负数，把问题中与数量有关的词语，用含有数字、字母和运算符号的式子表示出来，就是列代数式．
29．【分析】（1）将题中记录的数据相加，根据计算结果结合最后从A站出站即可解决问题．
（2）求出小王乘坐的站数之和即可解决问题．
【解答】解：（1）由题知，
因为+4﹣3+6﹣8+5﹣2﹣3+1＝0，且最后从A站出站，
所以A站是洪山广场站．
（2）因为|+4|+|﹣3|+|+6|+|﹣8|+|+5|+|﹣2|+|﹣3|+|+1|＝32，且相邻两站之间的平均距离为1.2千米，
所以32×1.2＝38.4（千米）．
答：小王志愿服务期间乘坐地铁行进的总路程约是38.4千米．
【点评】本题考查数轴及正数和负数，准确的计算是解题的关键．
30．【分析】（1）先去括号，再合并同类项求出代数式M的最简结果，根据非负数的性质可求出x，y的值，代入计算即可．
（2）将代数式化为（2﹣2b）x2+（a+3）x﹣6y+7，则可得2﹣2b＝0，a+3＝0，求出a，b的值，即可得出答案．
【解答】解：∵A＝2x2﹣2x﹣1，B＝﹣x2+xy+1，
∴M＝4A﹣（3A﹣2B）
＝4A﹣3A+2B
＝A+2B
＝2x2﹣2x﹣1+2（﹣x2+xy+1）
＝2x2﹣2x﹣1﹣2x2+2xy+2
＝﹣2x+2xy+1．
∵（x+1）2+|y﹣2|＝0，
∴x+1＝0，y﹣2＝0，
解得x＝﹣1，y＝2．
将x＝﹣1，y＝2代入原式，
得M＝﹣2×（﹣1）+2×（﹣1）×2+1＝2﹣4+1＝﹣1．
（2）（2x2+ax﹣y+6）﹣（2bx2﹣3x+5y﹣1）
＝2x2+ax﹣y+6﹣2bx2+3x﹣5y+1
＝（2﹣2b）x2+（a+3）x﹣6y+7，
∵代数式（2x2+ax﹣y+6）﹣（2bx2﹣3x+5y﹣1）的值与字母x的取值无关，
∴2﹣2b＝0，a+3＝0，
解得a＝﹣3，b＝1．
∴2a﹣b＝2×（﹣3）﹣1＝﹣6﹣1＝﹣7．
【点评】本题考查整式的加减﹣化简求值、非负数的性质：绝对值、偶次方，熟练掌握运算法则是解答本题的关键．
31．【分析】（1）根据a是最大的负整数，b是﹣5的相反数可求出a，b的值，再表示在数轴上即可；
（2）P表示的数为﹣1+3t，Q表示的数为5+t，可得：﹣1+3t＝5+t，即可解得答案．
【解答】解：（1）∵a是最大的负整数，b是﹣5的相反数，
∴a＝﹣1，b＝5；
如图：
（2）P表示的数为﹣1+3t，Q表示的数为5+t，
根据题意得：﹣1+3t＝5+t，
解得：t＝3，
∴t的值为3．
【点评】本题考查数轴，一元一次方程的应用，解题的关键是用含t的代数式表示P，Q所表示的数．
32．【分析】（1）由所给的数不难得出，第一组的第n个数为：（﹣1）n•2n，第二组的数等于第一组相应的数减3，第三组的数等于第一组的相应的数除以（﹣4），从而可求解；
（2）结合（1）进行求解即可；
（3）分别表示出各组的数，得出关于k的方程，解方程即可．
【解答】解：（1）由题意得：第一组的第n个数为：（﹣1）n•2n，
第二组的数等于第一组相应的数减3，即：（﹣1）n•2n﹣3；
第三组的数等于第一组的相应的数除以（﹣4），即：，
∴第一组第7个数是：﹣14，
第二组第7个数是：﹣14﹣3＝﹣17，
第三组第7个数是：，
故答案为：﹣14，﹣17，；
（2）由（1）可得：第二组的第n个数是：（﹣1）n•2n﹣3，
第三组第n个数是：，
故答案为：（﹣1）n•2n﹣3和；
（3）设第一组的第k个数为x，则第二组的第k个数为x﹣3，第三组第k个数为，
列方程得：，
解得x＝100，
∴（﹣1）k•2k＝100，
解得：k＝50．
【点评】本题主要考查数字的变化类规律，解答的关键是分析清楚所给的数字之间的规律．
第2次
第3次
第4次
第5次
第6次
第7次
+1
﹣8
+5
+4
+5
n