









所属成套资源:2025年新高考数学【北师大版】大一轮复习讲义【配套PPT+教师版+学生版+同步练习】
第四章 §4.10 解三角形应用举例-【北师大版】2025年高考数学大一轮复习(课件+讲义+练习)
展开
这是一份第四章 §4.10 解三角形应用举例-【北师大版】2025年高考数学大一轮复习(课件+讲义+练习),文件包含第四章§410解三角形应用举例-北师大版2025数学大一轮复习课件pptx、第四章§410解三角形应用举例-北师大版2025数学大一轮复习讲义练习docx、第四章§410解三角形应用举例-北师大版2025数学大一轮复习讲义教师版docx、第四章§410解三角形应用举例-北师大版2025数学大一轮复习讲义学生版docx等4份课件配套教学资源,其中PPT共60页, 欢迎下载使用。
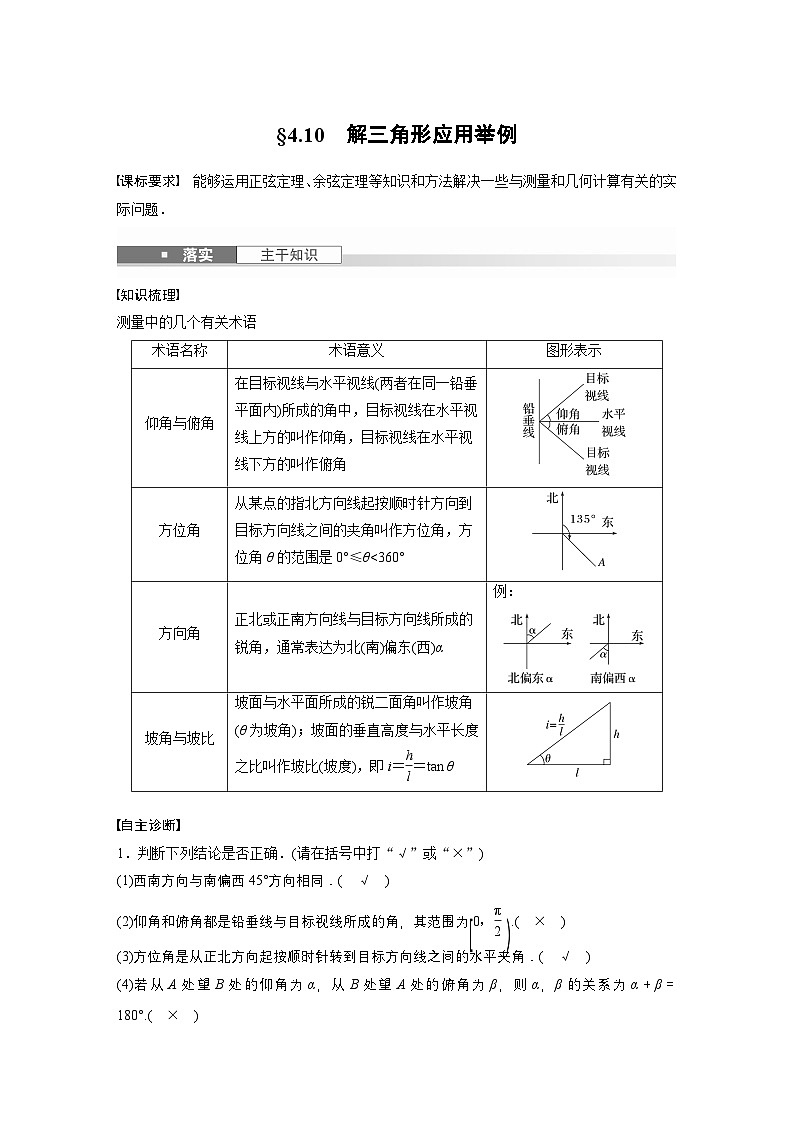
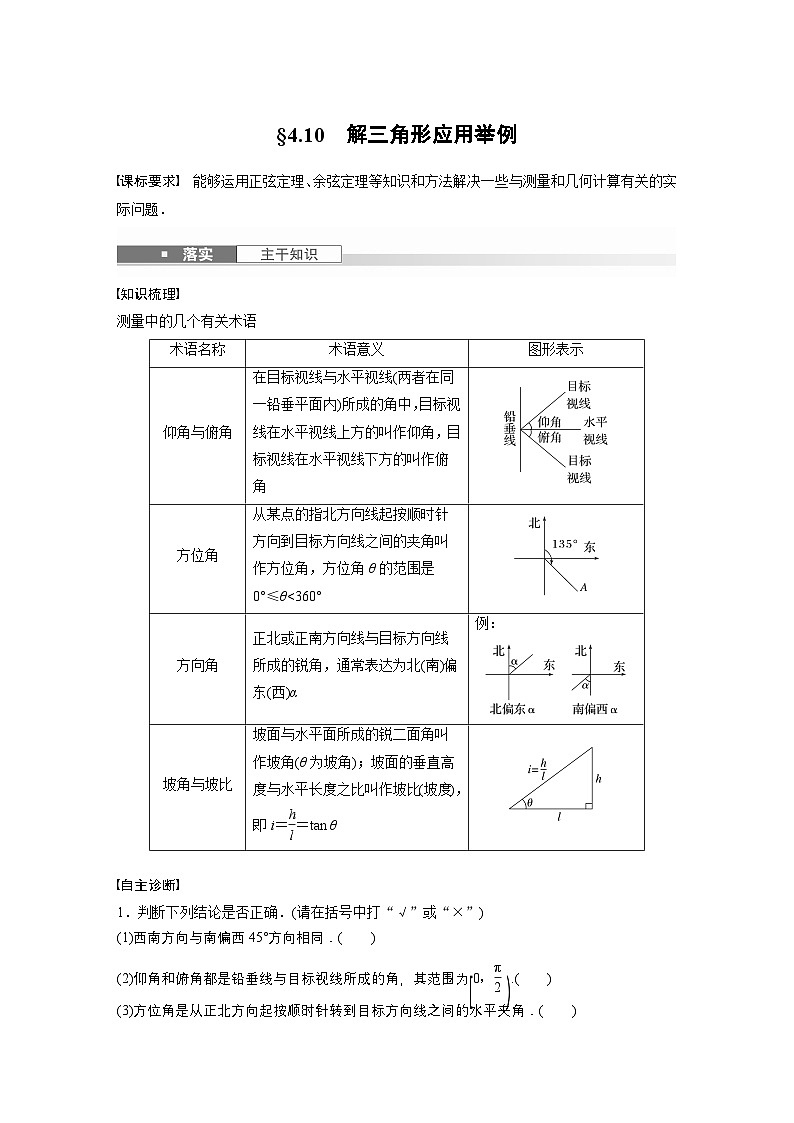
能够运用正弦定理、余弦定理等知识和方法解决一些与测量和几何计算有关的实际问题.
第一部分 落实主干知识
第二部分 探究核心题型
1.判断下列结论是否正确.(请在括号中打“√”或“×”)(1)西南方向与南偏西45°方向相同.( )(2)仰角和俯角都是铅垂线与目标视线所成的角,其范围为 .( )(3)方位角是从正北方向起按顺时针转到目标方向线之间的水平夹角.( )(4)若从A处望B处的仰角为α,从B处望A处的俯角为β,则α,β的关系为α+β=180°.( )
2.如图,两座灯塔A和B与海岸观察站C的距离相等,灯塔A在观察站南偏西40°方向,灯塔B在观察站南偏东60°方向,则灯塔A在灯塔BA.北偏东10°方向 B.北偏西10°方向C.南偏东80°方向 D.南偏西80°方向
由题可知,∠CAB=∠CBA=40°,又∠BCD=60°,所以∠CBD=30°,所以∠DBA=10°,因此灯塔A在灯塔B南偏西80°方向.
3.如图所示,为测量某树的高度,在地面上选取A,B两点,从A,B两点分别测得树尖P的仰角为30°,45°,且A,B两点之间的距离为60 m,则树的高度为
在△ABP中,∠APB=45°-30°=15°,
由题意可知∠ACB=60°,
例1 (1)如图,某市地面有四个5G基站A,B,C,D.已知基站C,D建在江的南岸,距离为10 km;基站A,B建在江的北岸,测得∠ACB=45°,∠ACD=30°,∠ADC=120°,∠ADB=75°,则基站A,B之间的距离为
在△ACD中,∠ACD=30°,∠ADC=120°,又∠ADB=75°,
在△BCD中,∠CBD=180°-(30°+45°+45°)=60°,
在△ABD中,由余弦定理得AB2=AD2+BD2-2AD·BD·cs∠ADB
(2)(2024·厦门模拟)一艘海轮从A处出发,以每小时40海里的速度沿东偏南50°方向直线航行,30分钟后到达B处.在C处有一座灯塔,海轮在A处观察灯塔,其方向是东偏南20°,在B处观察灯塔,其方向是北偏东65°,那么B,C两点间的距离是
依题意,如图,在△ABC中,
距离问题的解题思路:这类实际应用题,实质就是解三角形问题,一般都离不开正弦定理和余弦定理,在解题中,首先要正确地画出符合题意的示意图,然后将问题转化为三角形问题去求解.注意:①基线的选取要恰当准确;②选取的三角形及正、余弦定理要恰当.
跟踪训练1 (1)(2023·绥化模拟)安邦河,在黑龙江省内有两条.一条属于松花江二级支流,位于黑龙江省中部,发源于小兴安岭支脉平顶山西坡;另一条属于松花江右岸支流,位于黑龙江省东部,发源于完达山支脉分水岗,自南向北流经双鸭山、集贤、桦川3个市县,在桦川县新城乡境内注入松花江.安邦河从双鸭山一中旁流过,其中一河段的两岸基本上是平行的,根据城建工程计划,需要测量出该河段的宽度,现在一侧岸边选取两点A,B并测得AB=a,选取对岸一目标点C并测得∠ABC=α,∠BAC=β,则该段河流的宽度为
在△ABC中,由正弦定理得
(2)如图,为计算湖泊岸边两景点B与C之间的距离,在岸上选取A和D两点,现测得AB=5 km,AD=7 km,∠ABD=60°,∠CBD=23°,∠BCD=117°,据以上条件可求得两景点B与C之间的距离为______ km(精确到0.1 km,参考数据:sin 40°≈0.643,sin 117°≈0.891).
在△ABD中,有AB=5,AD=7,∠ABD=60°,由余弦定理可得,AD2=AB2+BD2-2AB·BDcs∠ABD,
整理可得BD2-5BD-24=0,解得BD=8或BD=-3(舍去).在△BCD中,有BD=8,∠CBD=23°,∠BCD=117°,所以∠BDC=180°-∠BCD-∠CBD=40°.
例2 (1)(2023·济宁统考)首钢滑雪大跳台(如图1)是冬奥历史上第一座与工业遗产再利用直接结合的竞赛场馆,大跳台的设计中融入了世界文化遗产敦煌壁画中“飞天”的元素.某校研究性学习小组为了估算赛道造型最高点A(如图2)距离地面的高度AB(AB与地面垂直),在赛道一侧找到一座建筑物PQ,测得PQ的高度为25.4米,并从P点测得A点的仰角为30°;在赛道与建筑物PQ之间的地面上的点M处测得A点,P点的仰角分别为75°和30°(其中B,M,Q三点共线),该学习小组利用这些数据估算得赛道造型最高点A距离地面的高度约为A.58 米 B.60 米C.66 米 D.68 米
由题意得∠AMB=75°,∠PMQ=30°,∠AMP=75°,∠APM=60°,∠PAM=45°,
在△PAM中,由正弦定理得
在△ABM中,AB=AM·sin∠AMB
(2)矗立在上饶市市民公园(如图1)的四门通天铜雕有着“四方迎客、通达天下”的美好寓意,也象征着上饶四省通衢,连南接北,通江达海,包容八方.如图2,某中学研究性学习小组为测量其高度,在和它底部O位于同一水平高度的共线三点A,B,C处测得铜雕顶端P处的仰角分别为 ,且AB=BC=20 m,则四门通天的高度为
在△BCO中,由余弦定理得
因为∠ABO+∠OBC=π,
高度问题的易错点(1)图形中为空间关系,极易当作平面问题处理,从而致错;(2)对仰角、俯角等概念理解不够深入,从而把握不准已知条件而致错.
跟踪训练2 (1)如图,在山脚A处测得山顶P的仰角为37°,沿坡角为23°的斜坡向上走28 m到达B处,在B处测得山顶P的仰角为53°,且A,B,P,C,Q在同一平面,则山的高度约为(参考数据:sin 37°≈0.6)A.30 m B.32 mC.34 m D.36 m
∠BAQ=23°,∠BPA=∠QPA-∠BPC=53°-37°=16°,∠PAB=∠PAQ-∠BAQ=37°-23°=14°,∠PBA=180°-16°-14°=150°.
所以山的高度约为PQ=AP·sin 37°=50×0.6=30(m).
(2)“伦敦眼”坐落在英国伦敦泰晤士河畔,是世界上首座观景摩天轮,又称“千禧之轮”,该摩天轮的半径为6(单位:10 m),游客在乘坐舱P升到上半空鸟瞰伦敦建筑BC,伦敦眼与建筑之间的距离AB为12(单位:10 m),游客在乘坐舱P看建筑BC的视角为θ.当乘坐舱P在伦敦眼的最高点D时,视角θ=30°,则建筑BC的高度为__________.(单位:10 m)
当乘坐舱P在伦敦眼的最高点D时,如图所示,因为摩天轮的半径为6,所以AD=12,又AB=12,
因为∠DBA=45°,所以∠DBC=45°,因为∠CDB=θ=30°,所以∠DCB=180°-45°-30°=105°,
例3 已知在岛A南偏西38°方向,距岛A 3海里的B处有一艘救援艇.岛A处的一艘故障船正以10海里/小时的速度向岛A北偏西22°方向行驶,问救援艇朝何方向以多大速度行驶,恰好用0.5小时追赶上该故障船?
如图,设救援艇在C处追赶上故障船,D为岛A正南方向上一点,救援艇的速度为x海里/小时,结合题意知BC=0.5x,AC=5,∠BAC=180°-38°-22°=120°.
所以BC=0.5x=7,解得x=14.
所以∠ABC=38°,又∠BAD=38°,所以BC∥AD,故救援艇以14海里/小时的速度向正北方向行驶,恰好用0.5小时追赶上该故障船.
角度问题的解题方法首先应明确方向角的含义,在解应用题时,分析题意,分清已知与所求,再根据题意正确画出示意图,这是最关键、最重要的一步,通过这一步可将实际问题转化成可用数学方法解决的问题,解题中也要注意体会正、余弦定理“联袂”使用的优点.
跟踪训练3 (1)(2023·南京模拟)如图所示,在坡度一定的山坡A处测得山顶上一建筑物CD的顶端C对于山坡的斜度为15°,向山顶前进100 m到达B处,又测得C对于山坡的斜度为45°,若CD=50 m,山坡对于地平面的坡度为θ,则cs θ等于
在△ABC中,∠ACB=180°-∠BAC-∠ABC=180°-15°-135°=30°,
(2)甲船在A处观察乙船,乙船在它北偏东60°方向,相距a海里的B处,乙船向正北方向行驶,若甲船速度是乙船速度的 倍,甲船为了尽快追上乙船,朝北偏东θ方向前进,则θ=________.
如图,设两船在C处相遇,
又因为0°
相关课件
这是一份第四章 §4.9 解三角形中的最值与范围问题-【北师大版】2025年高考数学大一轮复习(课件+讲义+练习),文件包含第四章§49解三角形中的最值与范围问题-北师大版2025数学大一轮复习课件pptx、第四章§49解三角形中的最值与范围问题-北师大版2025数学大一轮复习讲义练习docx、第四章§49解三角形中的最值与范围问题-北师大版2025数学大一轮复习讲义教师版docx、第四章§49解三角形中的最值与范围问题-北师大版2025数学大一轮复习讲义学生版docx等4份课件配套教学资源,其中PPT共60页, 欢迎下载使用。
这是一份第四章 §4.8 正弦定理、余弦定理-【北师大版】2025年高考数学大一轮复习(课件+讲义+练习),文件包含第四章§48正弦定理余弦定理-北师大版2025数学大一轮复习课件pptx、第四章§48正弦定理余弦定理-北师大版2025数学大一轮复习讲义练习docx、第四章§48正弦定理余弦定理-北师大版2025数学大一轮复习讲义教师版docx、第四章§48正弦定理余弦定理-北师大版2025数学大一轮复习讲义学生版docx等4份课件配套教学资源,其中PPT共60页, 欢迎下载使用。
这是一份第四章 §4.10 解三角形应用举例-2025年新高考数学一轮复习(课件+讲义+练习),文件包含第四章§410解三角形应用举例pptx、第四章§410解三角形应用举例教师版docx、第四章§410解三角形应用举例同步练习docx、第四章§410解三角形应用举例-2025新高考一轮复习讲义学生版docx等4份课件配套教学资源,其中PPT共60页, 欢迎下载使用。









