第七章　§7.6　空间向量的概念与运算-【北师大版】2025年高考数学大一轮复习（课件+讲义+练习）

这是一份第七章　§7.6　空间向量的概念与运算-【北师大版】2025年高考数学大一轮复习（课件+讲义+练习），文件包含第七章§76空间向量的概念与运算pptx、第七章§76空间向量的概念与运算-北师大版2025数学大一轮复习讲义练习docx、第七章§76空间向量的概念与运算-北师大版2025数学大一轮复习讲义教师版docx、第七章§76空间向量的概念与运算-北师大版2025数学大一轮复习讲义学生版docx等4份课件配套教学资源，其中PPT共60页， 欢迎下载使用。

1.了解空间向量的概念，了解空间向量的基本定理及其意义，掌握空间向量的正交分解及其坐标表示.2.掌握空间向量的线性运算及其坐标表示，掌握空间向量的数量积及其坐标表示，能用向量的数量积判断向量的共线和垂直.3.理解直线的方向向量及平面的法向量，能用向量方法证明立体几何中有关线面位置关系的一些简单定理.
第一部分 落实主干知识
第二部分 探究核心题型
1.空间向量的有关概念
2.空间向量的有关定理(1)共线向量基本定理：空间两个向量a，b(b≠0)共线的充要条件是存在唯一的实数λ，使得_______.(2)共面向量基本定理：如果两个向量a，b不共线，那么向量p与向量a，b共面的充要条件是存在 的有序实数对(x，y)，使得p＝______.(3)空间向量基本定理如果a，b，c是空间三个不共面的向量，p是空间任意一个向量，那么存在_____的三元有序实数组(x，y，z)，使得______________.
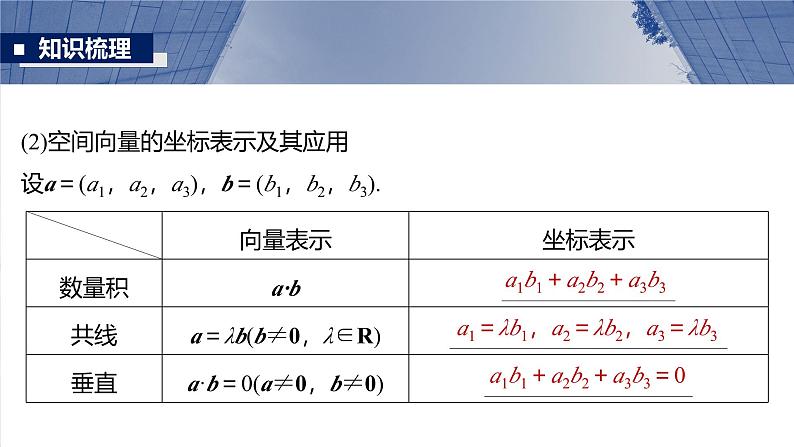
3.空间向量的数量积及运算律(1)数量积向量a，b的数量积a·b＝______________.
|a||b|cs〈a，b〉
(2)空间向量的坐标表示及其应用设a＝(a1，a2，a3)，b＝(b1，b2，b3).
a1b1＋a2b2＋a3b3
a1＝λb1，a2＝λb2，a3＝λb3
a1b1＋a2b2＋a3b3＝0
4.空间位置关系的向量表示(1)设点A，B是直线l上不重合的任意两点，称 为直线l的方向向量.(2)如果一条直线l与一个平面α垂直，那么就把直线l的 n叫作平面α的法向量.
(3)空间位置关系的向量表示
1.判断下列结论是否正确.(请在括号中打“√”或“×”)(1)空间中任意两个非零向量a，b共面.(　　)(2)空间中模相等的两个向量方向相同或相反.(　　)
(4)若直线a的方向向量和平面α的法向量平行，则a∥α.(　　)
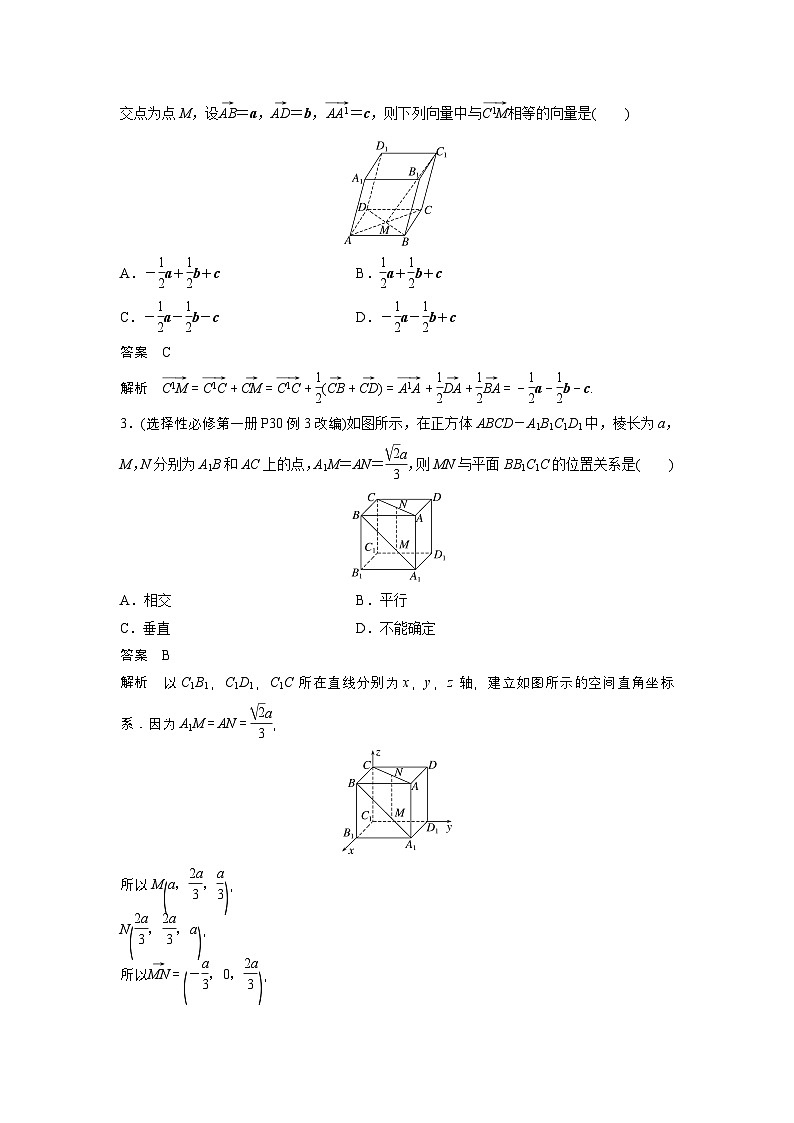
3.(选择性必修第一册P30例3改编)如图所示，在正方体ABCD－A1B1C1D1中，棱长为a，M，N分别为A1B和AC上的点，A1M＝AN＝ ，则MN与平面BB1C1C的位置关系是A.相交 B.平行C.垂直 D.不能确定
以C1B1，C1D1，C1C所在直线分别为x，y，z轴，建立如图所示的空间直角坐标系.
所以MN∥平面BB1C1C.
4.设直线l1，l2的方向向量分别为a＝(－2,2,1)，b＝(3，－2，m)，若l1⊥l2，则m＝______.
∵l1⊥l2，∴a⊥b，∴a·b＝－6－4＋m＝0，∴m＝10.
例1　(1)(2023·淮安模拟)设x，y是实数，已知三点A(1,5，－2)，B(2,4,1)，C(x,3，y＋2)在同一条直线上，那么x＋y等于A.2　　　B.3　　　C.4　　　D.5
题型一　空间向量的线性运算
因为A，B，C三点共线，所以存在唯一的实数λ，
用已知向量表示某一向量的三个关键点(1)要结合图形，以图形为指导是解题的关键.(2)要正确理解向量加法、减法与数乘运算的几何意义.(3)在立体几何中，三角形法则、平行四边形法则仍然成立.
跟踪训练1　(1)已知a＝(2,3，－4)，b＝(－4，－3，－2)，b＝ －2a，则x等于A.(0,3，－6) B.(0,6，－20)C.(0,6，－6) D.(6,6，－6)
由b＝ －2a，得x＝4a＋2b＝(8,12，－16)＋(－8，－6，－4)＝(0,6，－20).
(2)如图，在长方体ABCD－A1B1C1D1中，O为AC的中点.
例2　(1)下列命题正确的是A.若a与b共线，b与c共线，则a与c共线B.向量a，b，c共面，即它们所在的直线共面C.若空间向量a，b，c不共面，则a，b，c都不为0D.若a，b，c共面，则存在唯一的实数对(x，y)，使得a＝xb＋yc
题型二　空间向量基本定理及其应用
若b＝0，则满足a与b共线，b与c共线，但是a与c不一定共线，故A错误；因为向量是可以移动的量，所以向量a，b，c共面，但它们所在的直线不一定共面，故B错误；假设a，b，c至少有一个为0，则空间向量a，b，c共面，故假设不成立，故C正确；假设b＝0，若a，c共线，则存在无数个实数对(x，y)，使得a＝xb＋yc，若a，c不共线，则不存在实数对(x，y)，使得a＝xb＋yc，故D错误.
(2)(多选)下列说法中正确的是A.|a|－|b|＝|a＋b|是a，b共线的充要条件
由|a|－|b|＝|a＋b|，可知向量a，b的方向相反，此时向量a，b共线，反之，当向量a，b同向时，不能得到|a|－|b|＝|a＋b|，所以A不正确；
可得P，A，B，C四点共面，所以C正确；
所以A，B，C三点共线，反之也成立，即λ＋μ＝1是A，B，C三点共线的充要条件，所以D正确.
应用共线(面)向量定理证明点共线(面)的方法比较
由A，B，C，D四点共面，且其中任意三点均不共线，可得6－3＋λ＝1，解得λ＝－2.
由空间向量的共面向量基本定理可知，点E，A，C，D1四点共面，即点E在平面ACD1上，
由等体积法得 ＝ ，
例3　如图，已知平行六面体ABCD－A1B1C1D1中，底面ABCD是边长为1的正方形，AA1＝2，∠A1AB＝∠A1AD＝120°.(1)求线段AC1的长；
题型三　空间向量数量积及其应用
则|a|＝|b|＝1，|c|＝2，a·b＝0，c·a＝c·b＝2×1×cs 120°＝－1.
(2)求异面直线AC1与A1D夹角的余弦值；
＝a·b－a·c＋b2－c2＝0＋1＋1－4＝－2，
设异面直线AC1与A1D的夹角为θ，
(3)求证：AA1⊥BD.
空间向量的数量积运算有两条途径，一是根据数量积的定义，利用模与夹角直接计算；二是利用坐标运算.
∵P－ABC为正三棱锥，O为△ABC的中心，∴PO⊥平面ABC，
例4　如图所示，在长方体ABCD －A1B1C1D1中，AA1＝AD＝1，E为CD的中点.(1)求证：B1E⊥AD1；
题型四　向量法证明平行、垂直
(2)在棱AA1上是否存在一点P，使得DP∥平面B1AE？若存在，求AP的长；若不存在，说明理由.
存在满足要求的点P.假设在棱AA1上存在一点P(0,0，z0)，
设平面B1AE的法向量为n＝(x，y，z).
所以存在点P，满足DP∥平面B1AE，
(1)利用向量法证明平行、垂直关系，关键是建立恰当的坐标系(尽可能利用垂直条件，准确写出相关点的坐标，进而用向量表示涉及直线、平面的要素).(2)向量证明的核心是利用向量的数量积或数乘向量，但向量证明仍然离不开立体几何的有关定理.
跟踪训练4　如图，已知四棱锥P－ABCD的底面是平行四边形，侧面PAB是等边三角形，BC＝2AB，AC＝ ，PB⊥AC.(1)求证：平面PAB⊥平面ABCD；
所以AC2＋AB2＝BC2，所以AC⊥AB，又AC⊥PB，PB∩AB＝B，且PB，AB⊂平面PAB，所以AC⊥平面PAB，又AC⊂平面ABCD，所以平面PAB⊥平面ABCD.
(2)设Q为侧棱PD上一点，四边形BEQF是过B，Q两点的截面，且AC∥平面BEQF，是否存在点Q，使得平面BEQF⊥平面PAD？若存在，求 的值；若不存在，说明理由.
假设存在点Q，使得平面BEQF⊥平面PAD.取AB的中点为H，连接PH，则PH⊥AB，因为平面PAB⊥平面ABCD，平面PAB∩平面ABCD＝AB，所以PH⊥平面ABCD.建立如图所示的空间直角坐标系，
设n1＝(x1，y1，z1)是平面PAD的法向量，
连接EF，因为AC∥平面BEQF，AC⊂平面PAC，平面PAC∩平面BEQF＝EF，所以AC∥EF.
设n2＝(x2，y2，z2)是平面BEQF的法向量，
由平面BEQF⊥平面PAD知n1⊥n2，则n1·n2＝3λ＋3λ－4＝0，
一、单项选择题1.已知直线l的一个方向向量为m＝(x,2，－5)，平面α的一个法向量为n＝(3，－1,2)，若l∥α，则x等于A.－6　　　B.6　　　C.－4　　　D.4
若l∥α，则m⊥n，从而m·n＝0，即3x－2－10＝0，解得x＝4.
由长方体的性质可知AD⊥AB，AD⊥BB1，AD∥BC，AD＝BC＝1，
3.已知平面α内有一个点A(2，－1,2)，α的一个法向量为n＝(3,1,2)，则下列点P中，在平面α内的是
4.如图在一个120°的二面角的棱上有两点A，B，线段AC，BD分别在这个二面角的两个半平面内，且均与棱AB垂直，若AB＝ ，AC＝1，BD＝2，则CD的长为
5.(2022·全国乙卷)在正方体ABCD－A1B1C1D1中，E，F分别为AB，BC的中点，则A.平面B1EF⊥平面BDD1B.平面B1EF⊥平面A1BDC.平面B1EF∥平面A1ACD.平面B1EF∥平面A1C1D
在正方体ABCD－A1B1C1D1中，AC⊥BD且DD1⊥平面ABCD，又EF⊂平面ABCD，所以EF⊥DD1，因为E，F分别为AB，BC的中点，所以EF∥AC，所以EF⊥BD，又BD∩DD1＝D，BD，DD1⊂平面BDD1，所以EF⊥平面BDD1，又EF⊂平面B1EF，所以平面B1EF⊥平面BDD1，故A正确；
如图，以点D为原点，建立空间直角坐标系，设AB＝2，则D(0,0,0)，B1(2,2,2)，E(2,1,0)，F(1,2,0)，B(2,2,0)，A1(2,0,2)，A(2,0,0)，C(0,2,0)，C1(0,2,2)，
设平面B1EF的法向量为m＝(x1，y1，z1)，
同理可得平面A1BD的一个法向量为n1＝(1，－1，－1)，平面A1AC的一个法向量为n2＝(1,1,0)，平面A1C1D的一个法向量为n3＝(1,1，－1)，则m·n1＝2－2＋1＝1≠0，
所以平面B1EF与平面A1BD不垂直，故B错误；因为m与n2不平行，所以平面B1EF与平面A1AC不平行，故C错误；因为m与n3不平行，所以平面B1EF与平面A1C1D不平行，故D错误.
6.已知梯形CEPD如图(1)所示，其中PD＝8，CE＝6，A为线段PD的中点，四边形ABCD为正方形，现沿AB进行折叠，使得平面PABE⊥平面ABCD，得到如图(2)所示的几何体.已知当点F满足 (0<λ<1)时，平面DEF⊥平面PCE，则λ的值为
由题意，以A为原点，AB，AD，AP所在直线分别为x轴、y轴、z轴，建立空间直角坐标系，如图所示，则D(0,4,0)，E(4,0,2)，C(4,4,0)，P(0,0,4)，A(0,0,0)，B(4,0,0)，
则(t,0,0)＝(4λ，0,0)，∴t＝4λ，∴F(4λ，0,0)，
设平面DEF的法向量为n＝(x，y，z)，
取x＝1，得n＝(1，λ，2λ－2)，设平面PCE的法向量为m＝(a，b，c)，
取a＝1，得m＝(1,1,2)，∵平面DEF⊥平面PCE，
二、多项选择题7.下列关于空间向量的命题中，正确的有A.若向量a，b与空间任意向量都不能构成一组基，则a∥bB.若非零向量a，b，c满足a⊥b，b⊥c，则有a∥c
D.若{a＋b，b＋c，c＋a}是空间的一组基，则{a，b，c}也是空间的 一组基
对于A，若向量a，b与空间任意向量都不能构成一组基，则a，b为共线向量，即a∥b，故A正确；对于B，若非零向量a，b，c满足a⊥b，b⊥c，则a与c不一定共线，故B错误；
可得A，B，C，D四点共面，故C正确；对于D，若{a＋b，b＋c，c＋a}是空间的一组基，则对空间中任意一个向量d，存在唯一实数组(x，y，z), 使d＝x(a＋b)＋y(b＋c)＋z(c＋a)＝(x＋z)a＋(x＋y)b＋(y＋z)c，则{a，b，c}也是空间的一组基，故D正确.
8.如图，在正方体ABCD－A1B1C1D1中，G为正方形A1B1C1D1的中心，E，F分别为AB，BB1的中点，下列结论正确的是A.C1D∥平面EFG
D.A1C⊥平面EFG
建立如图所示的空间直角坐标系，因为E是棱AB的中点，F是棱BB1的中点，G是正方形A1B1C1D1的中心，设正方体的棱长为1，
设平面EFG的法向量为n＝(x，y，z)，
令x＝1，∴n＝(1,2，－1)，
∴C1D∥平面EFG，故A选项正确；
三、填空题9.已知向量a＝(1,1,0)，则与a同向共线的单位向量e＝_____________.
因为向量a＝(1,1,0)，
故点C的坐标为(－5，－2,6).
如图，设BC的中点为E，连接AE，PE，PO，则O在AE上且AO＝2OE，
由于S，M，N，O四点共面，
四、解答题13.如图，四棱锥P－ABCD的底面为正方形，侧棱PA⊥底面ABCD，且PA＝AD＝2，E，F，H分别是线段PA，PD，AB的中点.求证：(1)PB∥平面EFH；
∵E，H分别是线段PA，AB的中点，∴PB∥EH.∵PB⊄平面EFH，且EH⊂平面EFH，∴PB∥平面EFH.
(2)PD⊥平面AHF.
建立如图所示的空间直角坐标系.则A(0,0,0)，D(0,2,0)，P(0,0,2)，F(0,1,1)，H(1,0,0).
∴PD⊥AF，PD⊥AH.
∵AH∩AF＝A，且AH，AF⊂平面AHF，∴PD⊥平面AHF.
(1)若O为AC的中点，求证：A1O⊥AO；
(2)若FP∥平面D1AE，求线段CP长度的最小值.
连接BD，由正方形的性质可得B，O，D三点共线，O为BD的中点，所以A1O⊥BD，
由(1)可知A1O⊥AO，AO，BD⊂平面ABCD，AO∩BD＝O，所以A1O⊥平面ABCD，以O为坐标原点，OA，OB，OA1所在直线分别为x轴、y轴、z轴建立如图所示的空间直角坐标系，则A(1,0,0)，D(0，－1,0)，A1(0,0,1)，B(0,1,0)，C(－1,0,0)，
设平面D1AE的法向量为n＝(x，y，z)，
令x＝3，则z＝7，y＝1.所以n＝(3,1,7)为平面D1AE的一个法向量，因为点P在平面ABCD内，故设点P的坐标为(m，n，0)，
又FP∥平面D1AE，
15.(多选)(2024·梅州模拟)如图，在正方体ABCD－A1B1C1D1中，AA1＝3，点M，N分别在棱AB和BB1上运动(不含端点).若D1M⊥MN，则下列命题正确的是A.MN⊥A1MB.MN⊥平面D1MCC.线段BN长度的最大值为D.三棱锥C1－A1D1M的体积不变
在正方体ABCD－A1B1C1D1中，以点D为原点，以DA，DC，DD1所在直线分别为x，y，z轴建立空间直角坐标系，如图，则A1(3,0,3)，D1(0,0,3)，C(0,3,0)，B(3,3,0)，设M(3，y,0)，N(3,3，z)，y，z∈(0,3)，
即CM与MN不垂直，从而MN与平面D1MC不垂直，故B错误；
对于D，连接A1C1，MC1，不论点M如何移动，点M到平面A1D1C1的距离均为3，
所以三棱锥C1－A1D1M的体积为定值，故D正确.
如图，建立空间直角坐标系，则C(0,2,0)，D1(0,0,2)，B(2,2,0)，设E(x,2，z)，x∈[0,2]，z∈[0,2]，
即x2＋(z－1)2＝1，x∈[0,2]，z∈[0,2]，则动点E的轨迹为以(0,2,1)为圆心，1为半径的半圆，