第九章　§9.3　统计案例-【北师大版】2025年高考数学大一轮复习（课件+讲义+练习）

这是一份第九章　§9.3　统计案例-【北师大版】2025年高考数学大一轮复习（课件+讲义+练习），文件包含第九章§93统计案例-北师大版2025数学大一轮复习课件pptx、第九章§93统计案例-北师大版2025数学大一轮复习讲义练习docx、第九章§93统计案例-北师大版2025数学大一轮复习讲义教师版docx、第九章§93统计案例-北师大版2025数学大一轮复习讲义学生版docx等4份课件配套教学资源，其中PPT共60页， 欢迎下载使用。

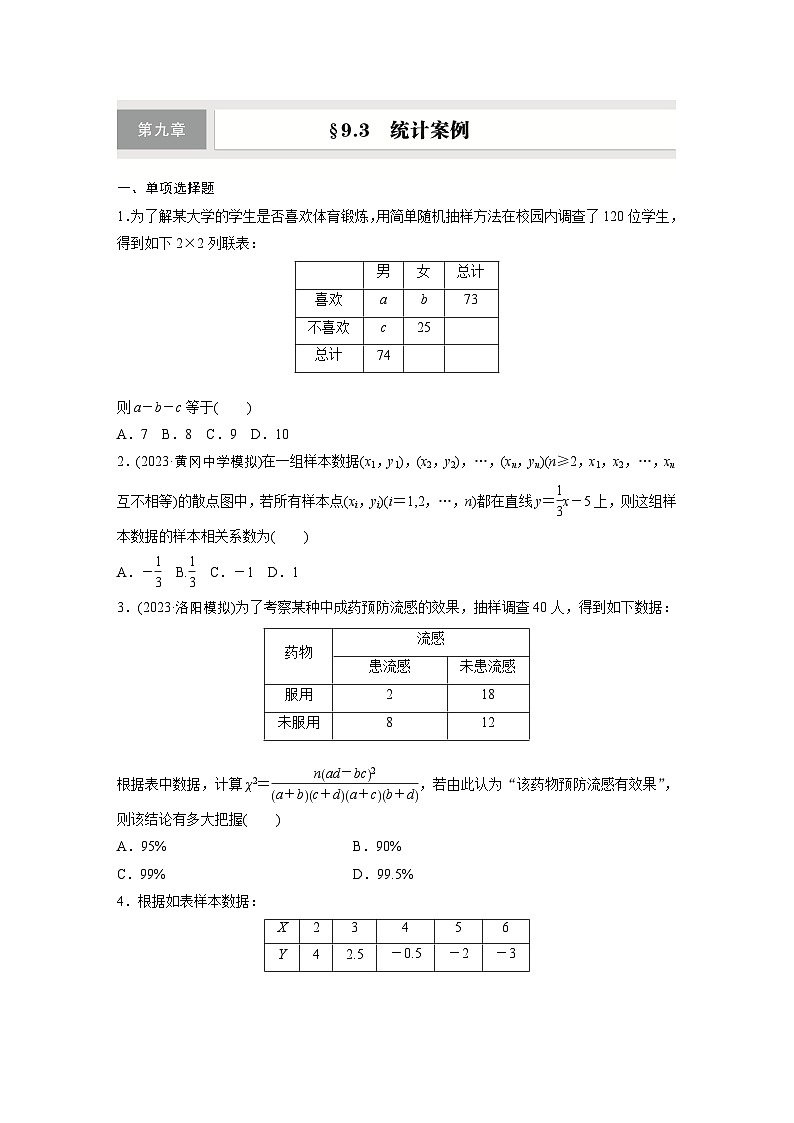
1.了解样本相关系数的统计含义.2.了解一元线性回归模型和2×2列联表，会运用这些方法解决简单的实际问题.3.会利用统计软件进行数据分析.
第一部分 落实主干知识
第二部分 探究核心题型
1.变量的相关关系(1)相关关系：两个变量 ，但又没有确切到可由其中的一个去精确地决定另一个的程度，这种关系称为相关关系.(2)相关关系的分类： 和 .(3)线性相关：一般地，如果两个变量的取值呈现正相关或负相关，而且散点落在 附近，我们就称这两个变量线性相关.
(2)当r>0时，称成对样本数据 ；当r<0时，称成对样本数据 .(3)|r|≤1；当|r|越接近1时，成对样本数据的线性相关程度越 ；当|r|越接近0时，成对样本数据的线性相关程度越 .
(2)偏差：观测值减去 ，称为偏差.
4.列联表与独立性检验(1)一般地，假设有两个分类变量X和Y，它们的取值分别为{A1，A2}和{B1，B2}，其2×2列联表为
3.回归分析和独立性检验都是基于成对样本观测数据进行估计或推断，得出的结论都可能犯错误.
1.判断下列结论是否正确.(请在括号中打“√”或“×”)(1)散点图是判断两个变量相关关系的一种重要方法和手段.(　　)(2)回归直线Y＝　　　至少经过点(x1，y1)，(x2，y2)，…，(xn，yn)中的一个点.(　　)(3)样本相关系数的绝对值越接近1，成对样本数据的线性相关程度越强.(　　)(4)若事件X，Y关系越密切，则由观测数据计算得到的χ2的值越小.(　　)
2.(多选)(2023·石嘴山模拟)下列有关回归分析的说法中正确的是A.相关关系是一种确定性的关系B.回归直线就是散点图中经过样本数据点最多的那条直线C.当样本相关系数r>0时，两个变量正相关D.两个变量的线性相关性越弱，|r|越接近于0
相关关系是一种不确定的关系，故A错；回归直线在散点图中可能不经过任一样本数据点，故B错；当样本相关系数r>0时，两个变量正相关，故C对；两个变量的线性相关性越弱，|r|越接近于0，故D对.
若由表中数据得到线性回归方程为Y＝0.8X＋ ，则当x＝10时的偏差为________(注：观测值减去预测值称为偏差).
3.(2023·福州统考)已知变量X和Y的统计数据如表：
所以当x＝10时的偏差为6.5－6.6＝－0.1.
4.某高校“统计初步”课程的教师随机调查了选该课的一些学生的情况，具体数据如表所示：
因为χ2>3.841，所以有95%的把握认为主修专业与性别有关.
题型一　成对数据的相关性
例1　(1)(2023·天津)调查某种群花萼长度和花瓣长度，所得数据如图所示，其中样本相关系数r＝0.824 5，则下列说法正确的是A.花瓣长度和花萼长度没有相关性B.花瓣长度和花萼长度呈负相关C.花瓣长度和花萼长度呈正相关D.若从样本中抽取一部分，则这部分的　样本相关系数一定是0.824 5
根据散点的集中程度可知，花瓣长度和花萼长度有相关性，故A错误；散点的分布是从左下到右上，从而花瓣长度和花萼长度呈正相关，故B错误，C正确；
由于r＝0.824 5是全部数据的样本相关系数，取出来一部分数据，相关性可能变强，可能变弱，即取出的数据的样本相关系数不一定是0.824 5，故D错误.
(2)(多选)(2023·湛江模拟)某服装生产商为了解青少年的身高和体重的关系，在15岁的男生中随机抽测了10人的身高和体重，数据如表所示：
由表中数据制作成如图所示的散点图，
因为离群点(168,89)的横坐标168小于平均值173.5，纵坐标89相对过大，所以去掉离群点后回归直线的斜率变大，
去掉离群点后成对样本数据的线性相关程度更强，拟合效果会更好，所以r1判定两个变量相关性的方法(1)画散点图：若点的分布从左下角到右上角，则两个变量正相关；若点的分布从左上角到右下角，则两个变量负相关.(2)样本相关系数：当r>0时，正相关；当r<0时，负相关；|r|越接近1，相关性越强.
跟踪训练1　(1)(2023·保定模拟)已知两个变量X和Y之间有线性相关关系，经调查得到样本数据如表所示：
由已知数据可知y随着x的增大而减小，
(2)对四组数据进行统计，获得如图所示的散点图，关于其样本相关系数的比较，正确的是
A.r2由散点图知图(1)与图(3)是正相关，故r1>0，r3>0，图(2)与图(4)是负相关，故r2<0，r4<0，且图(1)与图(2)的样本点集中在一条直线附近，因此r2例2　(2023·广州模拟)2022年底以来，发放消费券在全国多个地区流行，此举助力消费复苏.记发放的消费券额度为X(百万元)，带动的消费为Y(百万元).下表为某省随机抽查的一些城市的数据：
(1)根据表中的数据，请用样本相关系数说明Y与X有很强的线性相关关系，并求出Y关于X的线性回归方程；
说明：对于线性回归方程的样本相关系数r，当|r|>0.75时，两个变量之间具有很强的线性相关关系.参考数据：　 ≈5.9.
由于|r|>0.75且r非常接近1，所以y与x具有很强的线性相关关系.
所以所求线性回归方程为Y＝3.45X＋0.75.
(2)①若该省A城市在2023年8月份准备发放一轮额度为10百万元的消费券，利用(1)中求得的线性回归方程，预计可以带动多少消费？
当x＝10时，y＝3.45×10＋0.75＝35.25，所以预计能带动的消费达35.25百万元.
②当实际值与估计值的差的绝对值与估计值的比值不超过10%时，认为发放的该轮消费券助力消费复苏是理想的.若该省A城市8月份发放额度为10百万元的消费券后，经过一个月的统计，发现实际带动的消费为30百万元，请问发放的该轮消费券助力消费复苏是否理想？若不理想，请分析可能存在的原因.
所以发放的该轮消费券助力消费复苏不理想.发放消费券只是影响消费的其中一个因素，还有其他重要因素，比如：A城市经济发展水平不高，居民的收入水平直接影响了居民的消费水平；A城市人口数量有限、商品价格水平、消费者偏好、消费者年龄构成等因素一定程度上影响了消费总量.(只要写出一个原因即可).
(1)求Y关于X的线性回归方程；
所以线性回归方程为Y＝0.15X－7.5.
(2)已知服装店每天的经济效益W＝　　＋mx(k>0，m>0)，该商场现有60～150 m2的商铺出租，根据(1)的结果进行预测，要使单位面积的经济效益Z最高，小李应该租多大面积的商铺？
则f(x)＝g(t)＝0.15t－7.5t2＝－7.5×(t－0.01)2＋0.000 75，当t＝0.01，即x＝100时，f(x)取最大值，
又因为k>0，m>0，所以此时Z也取最大值，因此，小李应该租100 m2的商铺.
题型三　列联表与独立性检验
例3　(2023·全国甲卷)一项试验旨在研究臭氧效应，试验方案如下：选40只小白鼠，随机地将其中20只分配到试验组，另外20只分配到对照组，试验组的小白鼠饲养在高浓度臭氧环境，对照组的小白鼠饲养在正常环境，一段时间后统计每只小白鼠体重的增加量(单位：g).试验结果如下：对照组的小白鼠体重的增加量从小到大排序为15.2　18.8　20.2　21.3　22.5　23.2　25.826.5　27.5　30.1　32.6　34.3　34.8　35.635.6　35.8　36.2　37.3　40.5　43.2
试验组的小白鼠体重的增加量从小到大排序为7.8　9.2　11.4　12.4　13.2　15.5　16.518.0　18.8　19.2　19.8　20.2　21.6　22.823.6　23.9　25.1　28.2　32.3　36.5(1)计算试验组的样本平均数；
(2)①求40只小白鼠体重的增加量的中位数m，再分别统计两样本中小于m与不小于m的数据的个数，完成如下列联表：
依题意，可知这40只小白鼠体重的中位数是将两组数据合在一起，从小到大排列后第20位与第21位数据的平均数，由原数据可得第20位数据为23.2，第21位数据为23.6，
②根据①中的列联表，能否有95%的把握认为小白鼠在高浓度臭氧环境中与在正常环境中体重的增加量有差异？
所以有95%的把握认为小白鼠在高浓度臭氧环境中与在正常环境中体重的增加量有差异.
独立性检验的一般步骤(1)根据样本数据制成2×2列联表.
(3)比较χ2与临界值的大小关系，作统计推断.
跟踪训练3　(2024·哈尔滨模拟)由中央电视台综合频道(CCTV－1)和唯众传媒联合制作的《开讲啦》是中国首档青年电视公开课.每期节目由一位知名人士讲述自己的故事，分享他们对于生活和生命的感悟，给予中国青年现实的讨论
和心灵的滋养，讨论青年们的人生问题，同时也在讨论青春中国的社会问题，受到了青年观众的喜爱.为了了解观众对节目的喜爱程度，电视台随机调查了A，B两个地区的100名观众，得到如表所示的2×2列联表.
已知在被调查的100名观众中随机抽取1名，该观众来自B地区且喜爱程度为“非常喜欢”的概率为0.35.(1)现从100名观众中根据喜爱程度用分层随机抽样的方法抽取20名进行
问卷调查，则应抽取喜爱程度为“非常喜欢”的A，B地区的人数各是多少？
由题意得来自B地区且喜爱程度为“非常喜欢”的观众为0.35×100＝35(人)，
(2)完成上述表格，是否有95%的把握认为观众的喜爱程度与所在地区有关？
所以没有95%的把握认为观众的喜爱程度与所在地区有关.
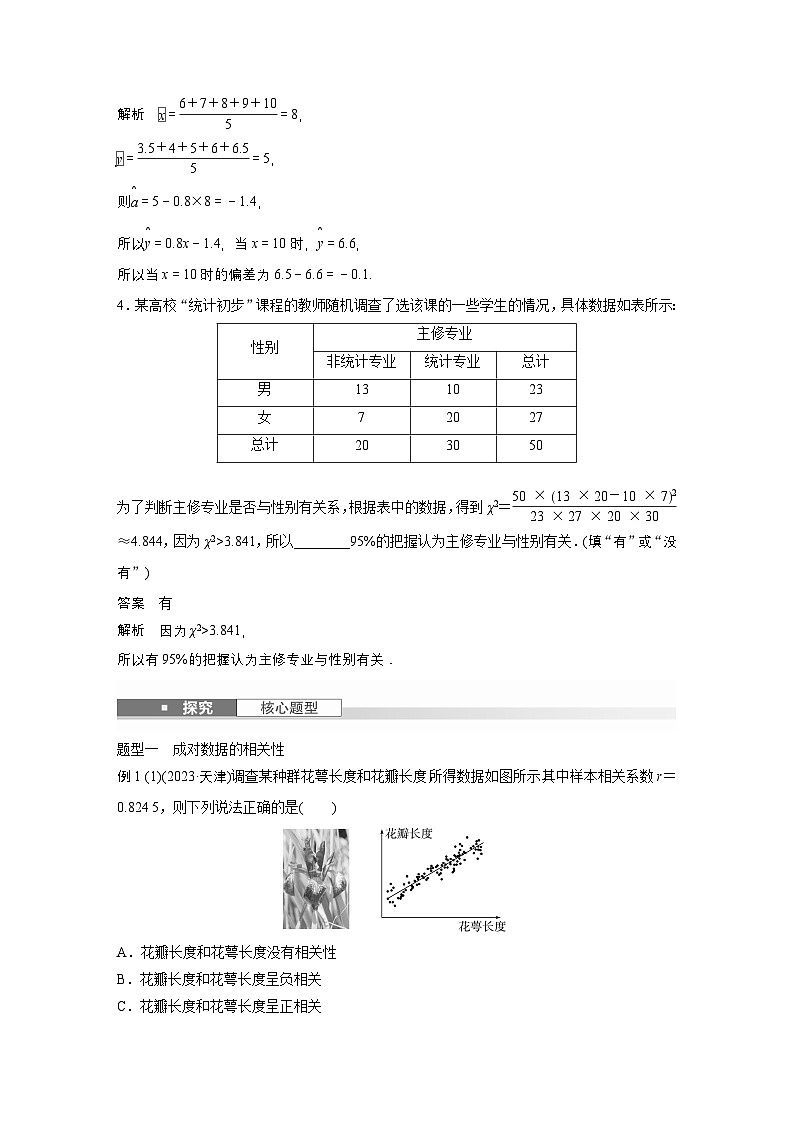
一、单项选择题1.为了解某大学的学生是否喜欢体育锻炼，用简单随机抽样方法在校园内调查了120位学生，得到如下2×2列联表：
则a－b－c等于A.7 　　　B.8　　　 C.9 　　　D.10
根据题意，可得c＝120－73－25＝22，a＝74－22＝52，b＝73－52＝21，∴a－b－c＝52－21－22＝9.
则这组样本数据完全正相关，且样本相关系数为1.
A.95% B.90% C.99% D.99.5%
3.(2023·洛阳模拟)为了考察某种中成药预防流感的效果，抽样调查40人，得到如下数据：
所以有95%的把握认为“该药物预防流感有效果”.
4.根据如表样本数据：
5.某中学调查了高一年级学生的选科倾向，随机抽取300人，其中选考物理的有220人，选考历史的有80人，统计各选科人数如表，则下列说法正确的是
A.物理类的学生中选择政治的比例比历史类的学生中选择政治的比例高B.物理类的学生中选择地理的比例比历史类的学生中选择地理的比例高C.选择生物与选考类别无关D.有99%的把握认为选择生物与选考类别有关
对于C和D，根据已知数据可得2×2列联表如表：
即认为选择生物与选考类别无关，故选项C正确，选项D不正确.
用最小二乘法求得Y关于X的线性回归方程是Y＝－0.32X＋ ，样本相关系数r＝－0.992 3，则下列说法不正确的是A.变量X与Y负相关且相关性很强B. ＝40C.当x＝85时，y的估计值为15D.对应点(105,6)的偏差为－0.4
6.某市物价局派人对5个商场某商品同一天的销售量及其价格进行调查，得到该商品的售价X(元)和销售量Y(件)之间的一组数据如表所示：
由线性回归方程可得变量X与Y负相关，且由样本相关系数|r|＝0.992 3，可知相关性很强，故A正确；
当x＝85时，y＝－0.32×85＋40＝12.8，故C错误；对应点(105,6)的偏差为6－(－0.32×105＋40)＝－0.4，故D正确.
二、多项选择题7.(2024·厦门模拟)为了有针对性地提高学生体育锻炼的积极性，某中学需要了解性别因素是否对本校学生体育锻炼的经常性有影响，随机抽取了300名学生，对他们是否经常锻炼的情况进行了调查，调查发现经常锻炼人数是不经常锻炼人数的2倍，绘制其等高堆积条形图，如图所示，则
A.参与调查的男生中经常锻炼的人数比不经　常锻炼的人数多B.从参与调查的学生中任取一人，已知该学　生为女生，则该学生经常锻炼的概率为C.有90%的把握认为性别因素影响学生体育锻炼的经常性D.假设调查人数为600人，经常锻炼人数与不经常锻炼人数的比例不变，　统计得到的等高堆积条形图也不变，有95%的把握认为性别因素影响　学生体育锻炼的经常性
由题意知经常锻炼人数是不经常锻炼人数的2倍，故经常锻炼人数为200人，不经常锻炼人数为100人，
故男生中经常锻炼的人数为200×0.5＝100(人)，不经常锻炼的人数为100×0.6＝60(人)，故男生中经常锻炼的人数比不经常锻炼的人数多，故A正确；
女生中经常锻炼的人数为200×0.5＝100(人)，不经常锻炼的人数为100×0.4＝40(人)，故从参与调查的学生中任取一人，已知该学生为女生，
由题意结合男、女生中经常锻炼和不经常锻炼的人数，可得列联表如表所示：
故没有90%的把握认为性别因素影响学生体育锻炼的经常性，故C错误；由题意可得
所以有95%的把握认为性别因素影响学生体育锻炼的经常性，故D正确.
8.沃柑，因其口感甜柔、低酸爽口，且营养成分高，成为大家喜欢的水果之一，目前主要种植于我国广西、云南、四川、湖南等地.得益于物流的快速发展，沃柑的销量大幅增长，同时刺激了当地农民种植沃柑的热情.根据对广西某地的沃柑种植面积情况进行调查，得到统计表如表所示：
根据此表，下列结论正确的是A.该地区这5年沃柑的种植面积的方差为212B.种植面积y与年份代码x的样本相关系数约为0.972(精确到0.001)C.Y关于X的线性回归方程为Y＝4.6X＋3.2D.预测该地区沃柑种植面积最早在2027年能突破40万亩
所以Y关于X的线性回归方程为Y＝4.6X＋3.2，故C正确；令4.6x＋3.2≥40，得x≥8，所以最小的整数为8,2 017＋8＝2 025，所以该地区沃柑种植面积最早在2025年能突破40万亩，故D错误.
三、填空题9.(2023·辽宁实验中学模拟)为了比较甲、乙、丙、丁四组数据的线性相关性的强弱，小明分别计算了甲、乙、丙、丁四组数据的样本相关系数，其数值分别为－0.95，－0.87,0.76,0.92，则这四组数据中线性相关性最强的是_____组数据.
根据题意，因为样本相关系数的绝对值越大，线性相关性越强.甲、乙、丙、丁四组数据的样本相关系数分别为－0.95，－0.87,0.76,0.92，所以甲组数据的线性相关性最强.
10.(2024·安庆模拟)对于数据组(xi，yi)(i＝1,2，…，n)，如果由线性回归方程得到的对应自变量xi的估计值是 ，那么将yi－ 称为对应点(xi，yi)的偏差.某商场为了给一种新商品进行合理定价，将该商品按事先拟定的价格进行试销，得到如表所示的数据：
根据表中的数据，得到销量Y(单位：件)与单价X(单位：元)之间的线性回归方程为Y＝－16X＋a，据计算，样本点(8.4,83)处的偏差为1.4，则m＝___.
由条件知当x2＝8.4时，y2＝83－1.4＝81.6，代入Y＝－16X＋a，解得a＝81.6＋16×8.4＝216，于是Y＝－16X＋216，
11.在某病毒疫苗的研发过程中，需要利用基因编辑小鼠进行动物实验.现随机抽取100只基因编辑小鼠对该病毒疫苗进行实验，得到如下2×2列联表(部分数据缺失)：
计算可知，有______的把握认为 “给基因编辑小鼠注射该种疫苗能起到预防该病毒感染的效果”.
完善2×2列联表如下：
所以有95%的把握认为“给基因编辑小鼠注射该种疫苗能起到预防该病毒感染的效果”.
12.为了考察某种药物预防疾病的效果，进行动物试验，得到如下列联表：
若在本次考察中得出“有99%的把握认为药物有效”的结论，则a的最小值为___.(其中a≥40且a∈N＋)
整理得(100a－4 000)2≥502×42×6.635，
解得a≥45.16或a≤34.84，
又因为a≥40且a∈N＋，所以a≥46，所以a的最小值为46.
四、解答题13.(2021·全国甲卷)甲、乙两台机床生产同种产品，产品按质量分为一级品和二级品，为了比较两台机床产品的质量，分别用两台机床各生产了200件产品，产品的质量情况统计如表：
(1)甲机床、乙机床生产的产品中一级品的频率分别是多少？
(2)是否有99%的把握认为甲机床的产品质量与乙机床的产品质量有差异？
所以有99%的把握认为甲机床的产品质量与乙机床的产品质量有差异.
14.(2023·绵阳模拟)移动物联网广泛应用于生产制造、公共服务、个人消费等领域.截至2022年底，我国移动物联网连接数达18.45亿户，成为全球主要经济体中首个实现“物超人”的国家.如图是2018－2022年移动物联网连接数W与年份代码T的散点图，其中年份2018－2022对应的T分别为1～5.
(1)根据散点图推断两个变量是否线性相关.计算样本相关系数(精确到0.01)，并推断它们的相关程度；
由图可知，两个变量线性相关.
因此，两个变量具有很强的线性相关性.
(2)求W关于T的经验回归方程，并预测2024年移动物联网连接数.