中职数学高教版（2021·十四五）基础模块 下册6.1 两点间距离公式和线段的中点坐标公式优质课ppt课件

这是一份中职数学高教版（2021·十四五）基础模块 下册6.1 两点间距离公式和线段的中点坐标公式优质课ppt课件，共16页。PPT课件主要包含了A1x10，A2x20，B10y1，B20y2，两点间距离公式，E0y，Fx0，Px0y0，典例2，解根据中点公式等内容，欢迎下载使用。
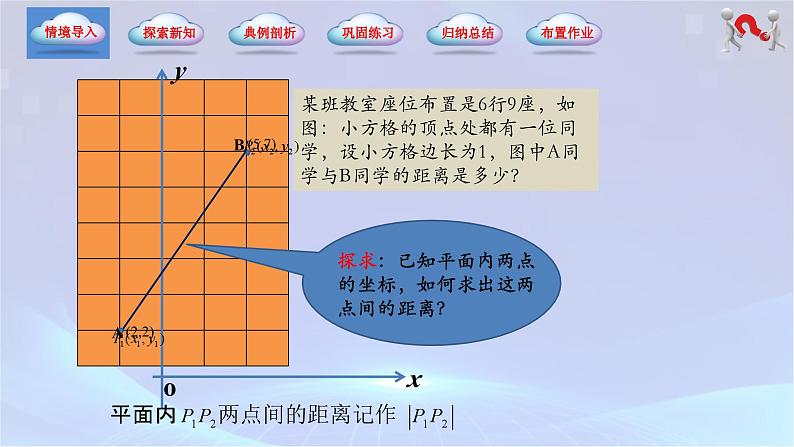
某班教室座位布置是6行9座，如图：小方格的顶点处都有一位同学，设小方格边长为1，图中A同学与B同学的距离是多少？
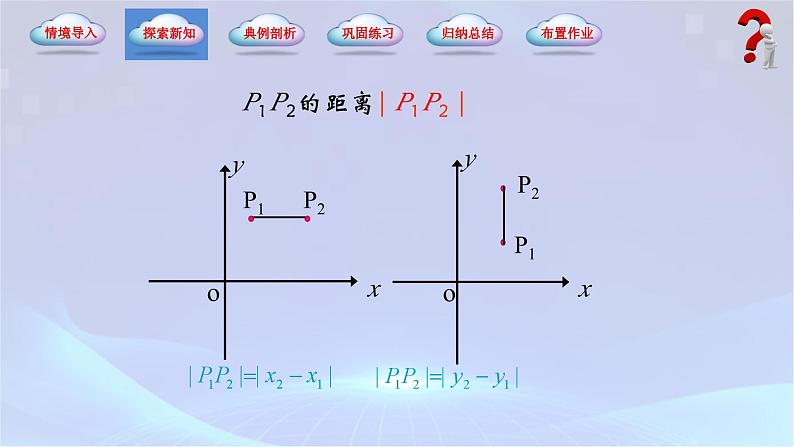
P1 P2的距离| P1 P2 |
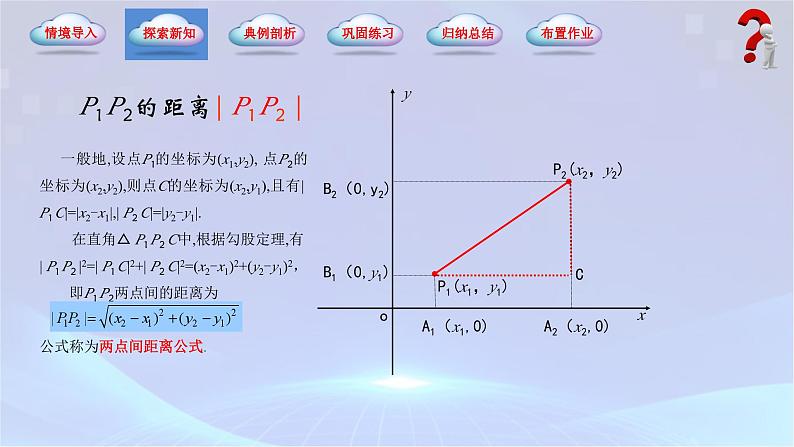
一般地,设点P1的坐标为(x1,y2), 点P2的坐标为(x2,y2),则点C的坐标为(x2,y1),且有| P1 C|=|x2-x1|,| P2 C|=|y2-y1|. 在直角△ P1 P2 C中,根据勾股定理,有| P1 P2 |2=| P1 C|2+| P2 C|2=(x2-x1)2+(y2-y1)2， 即P1 P2两点间的距离为公式称为两点间距离公式.
两点间的距离等于这两点横坐标之差的平方与纵坐标之差的平方和的算术平方根.
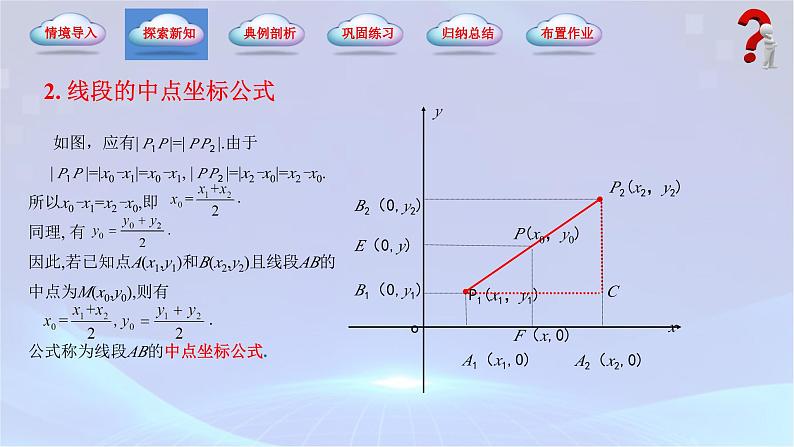
2. 线段的中点坐标公式
典例1计算M1(2, -5),M2(5,-1)两点间的距离.
典例3 求下列各题中连结两点的线段的中点坐标：（1）P1(6, -4),P2(-2,5);（2）A(a, 0),B(0,b);
典例4 如图，已知△ABC的三个顶点分别是A(2,4)、B(-1,1)、C(5,3). (1)求BC边上的中点D的坐标； (2)计算BC边上的中线的长度.
已知线段两个端点的坐标,可以确定线段中点的坐标.如果知道线段的一个端点和中点的坐标,能否确定另一个端点？怎么求它的坐标？