初中数学2 有理数的加减运算获奖备课课件ppt

这是一份初中数学2 有理数的加减运算获奖备课课件ppt，共15页。PPT课件主要包含了学习目标，情景导入，新知探究，尝试交流，同号两数相加，异号两数相加，取相同符号，概念归纳，课本例题，思考交流等内容，欢迎下载使用。

1.经历探索有理数加法法则的过程，体会分类和归纳的思想方法; 2.理解有理数的加法法则;（重点）3.能熟练地进行有理数加法的运算.（难点）
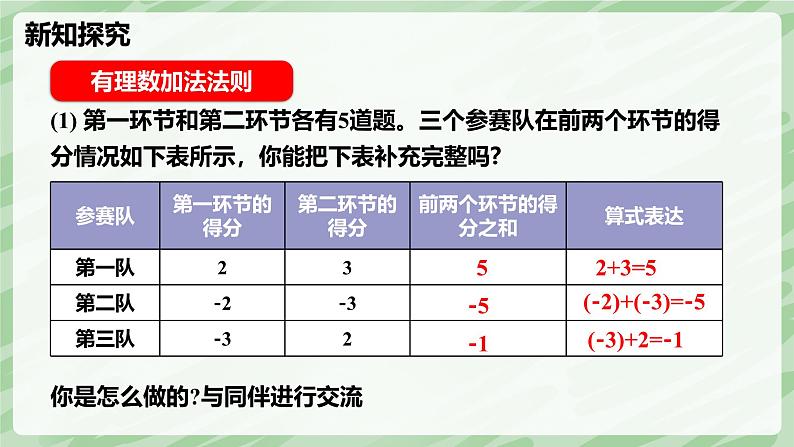
某班举行知识竞赛，评分标准是：答对一题加 1 分，答错一题扣 1 分，不回答得 0 分。
(+1)+(-1)=0
(-1)+(+1)=0
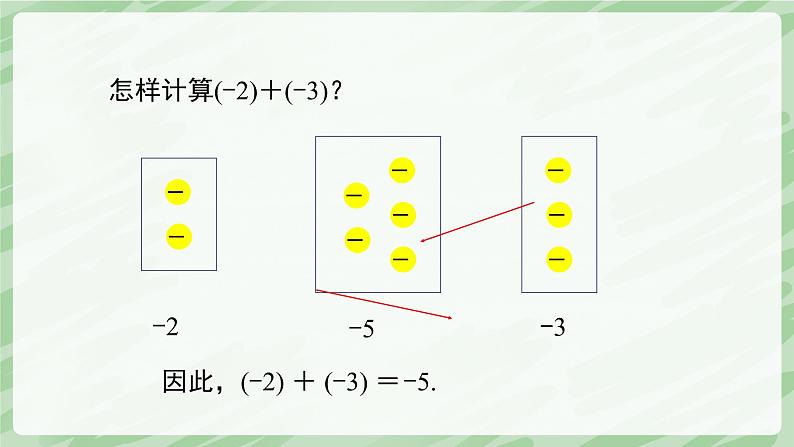
(1) 第一环节和第二环节各有5道题。三个参赛队在前两个环节的得分情况如下表所示，你能把下表补充完整吗?
(-2)+(-3)=-5
你是怎么做的?与同伴进行交流
如果我们用1个 表示＋1，用1个 表示－1，那么 直观表示： (+1)+(-1)=0，同样， 直观表示： (-1)+(+1)=0.
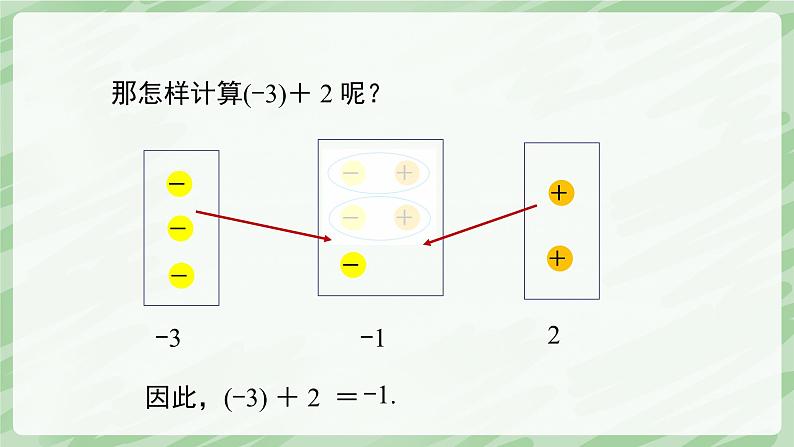
怎样计算(-2)＋(-3)？
因此，(-2) ＋ (-3) ＝
那怎样计算(-3)＋ 2 呢？
因此，(-3) ＋ 2 ＝
(3) 如果有第四个参赛队，那么第四队前两个环节的得分可能会出现哪些情形，据此可以列出哪些算式?
还有可能出现第一环节加3分，第二环节扣2分(或第一环节扣4分，第二环节加4分)等的情形。
你能用刚才的方法计算3＋( -2 )，( -4 )＋ 4 吗？
因此，3 ＋( -2 ) ＝
因此，( -4 ) ＋ 4 ＝
（1）两个有理数相加，有哪几种情形?你是怎么分类的？
（2）对于（1）中的每种情形，和是怎么确定的?
(-4)+(-8)= - (4+8) =-12
(-9)+(+2)= - (9-2)=-7
取绝对值较大的数的符号
两个加数的绝对值相加。
较大的绝对值减较小的绝对值。
和是综合加数的正负性和绝对值的大小关系确定的。
有理数加法法则同号两数相加，取相同的符号，并把绝对值相加.异号两数相加，绝对值相等时和为0;绝对值不等时，取绝对值较大的数的符号，并用较大的绝对值减较小的绝对值.一个数同0相加，仍得这个数.
取绝对值较大的数的符号，并用较大的绝对值减去较小的绝对值.
(1) 180＋(-10)； (2) (-10) ＋ (-1)；(3) 5＋(-5)； (4) 0＋(-2).
解：(1) 180＋(-10)
取相同的符号,并把绝对值相加.
(2) (-10)＋(-1)
(3) 5＋ (-5)
(4) 0＋(-2)
互为相反数的两数相加，和为0
一个数同0相加，仍得这个数.
(1)根据有理数加法法则，如果两个数互为相反数，那么它们的和等于0.反过来，如果两个数的和等于0，那么这两个数互为相反数吗?
(2)根据有理数加法法则进行正数或0的运算，得到的结果与小学数学中的加法运算一致吗?
(3)一个数加一个正数，所得的和与这个数有怎样的大小关系?一个数加一个负数呢?
一个数加一个正数，所得和大于这个数；一个数加一个负数，所得和小于这个数.
1.计算：
(1) (-25)＋(-7)； (2) (-13)＋ 5；(3) -23＋ 0； (4) 45＋(-45).
解：(1) (-25)＋ (-7)
(2) (-13)＋ 5
(3) (-23)＋ 0 ＝-23.
(4) 45＋(-45)＝0.
1. 按照有理数加法法则，计算15＋(－23)的正确过程是(　D　)
2. [新考法·逐项判断法·2023·遂宁]已知算式5□(－5)的值为0，则“□”内应填入的运算符号为(　A　)
3. [新考向·数学文化·2024·锦州期末]我国是最早进行负数运算的国家，魏晋时期的数学家刘徽在其著作《九章算术注》中，用不同颜色的算筹(小棍形状的记数工具)分别表示正数和负数(白色为正，黑色为负)，如图①表示的是(－13)＋(＋23)＝10的计算过程，则图②表示的计算过程是(　A　)
4. 在七年级举办的有奖竞猜活动中，成绩以100分为标准，超过的部分记为正数，不足的部分记为负数.按此方法记录了3名学生的成绩，具体数据为：＋3，－8，0，则这3名学生中的最高分是(　B　)
5. 若向北为正，则先向北走200 m，再向南走150 m，可以用算式表示为 ⁠.6. [情境题·生活应用·2024·金华期末]如图是同一时刻莫斯科与中国北京的时间，则当莫斯科时间为17：08时，北京时间为 ⁠.
＋200＋(－150)　
7. [2024济宁期末]下列是运用有理数加法法则计算－5＋2的思考、计算过程的叙述：①－5和2的绝对值分别为5和2；②－5的绝对值5较大，2的绝对值2较小；③－5＋2是异号两数相加；④结果的绝对值是用5－2得到的；⑤计算结果为－3；⑥结果的符号是取－5的符号——负号.请按运用法则思考、计算过程的先后顺序排序(只写序号)： ⁠.
③①②④⑥⑤或③①②⑥④⑤　
8.计算：(1)(－0.9)＋1.51；
【解】(－0.9)＋1.51＝1.51－0.9＝0.61.
(2)－77＋(－23)；
【解】－77＋(－23)＝－100.
(3)(－3.1)＋1.1；
【解】(－3.1)＋1.1＝－2.
9. 若两个数的和为正数，则这两个数(　A　)
10. 若｜ x ｜＝6，｜ y ｜＝4，则 x ＋ y 的值是(　D　)
11. [2024沧州期末]如图， M ， N ， P ， R 分别是数轴上四个整数所对应的点，其中有一点是原点，并且 MN ＝ NP ＝ PR ＝1.数 a 对应的点在 M 与 N 之间，数 b 对应的点在 P 与 R 之间，若｜ a ｜＋｜ b ｜＝3，则原点是 (　B　)
因为 MN ＝ NP ＝ PR ＝1，所以 MR ＝3.
①当原点在 N 点或 P 点时，因为数 a 对应的点在 M 与 N 之间，数 b 对应的点在 P 与 R 之间，所以｜ a ｜＋｜ b ｜＜3.因为｜ a ｜＋｜ b ｜＝3，所以原点不可能在 N 点或 P 点；
②当原点在 M 点或 R 点，且数 a 对应的点到 M 与数 b 对应的点到 R 的距 离相等时，｜ a ｜＋｜ b ｜＝3.综上所述，原点可能是点 M 或 R . 故选B.
12. [立德树人·抗洪抢险]在某次抗洪抢险中，解放军战士的冲锋舟沿东西方向的河流抢救灾民，早晨从甲村出发，晚上到达乙村，约定向东为正方向，当天的航行路程记录如下(单位：km)： ＋14，－10，＋8，－7，＋13，－6，＋12，－6. (1)请确定乙村相对于甲村的具体方位.
【解】因为(＋14)＋(－10)＋(＋8)＋(－7)＋(＋13)＋(－6)＋(＋12)＋(－6)＝14－10＋8－7＋13－6＋12－6 ＝18(km)，所以乙村位于甲村的正东方向，距离甲村18 km.
(2)救灾过程中，冲锋舟离出发地最远处有多远？
【解】第1次记录时冲锋舟离出发地的距离为｜＋14｜＝14(km)；第2次记录时冲锋舟离出发地的距离为｜14＋(－10)｜＝4(km)；第3次记录时冲锋舟离出发地的距离为｜4＋(＋8)｜＝12(km)；第4次记录时冲锋舟离出发地的距离为｜12＋(－7)｜＝5(km)；
第5次记录时冲锋舟离出发地的距离为｜5＋(＋13)｜＝18(km)；第6次记录时冲锋舟离出发地的距离为｜18＋(－6)｜＝12(km)；第7次记录时冲锋舟离出发地的距离为｜12＋(＋12)｜＝24(km)；第8次记录时冲锋舟离出发地的距离为｜24＋(－6)｜＝18(km).
由此可知，救灾过程中，冲锋舟离出发地最远处有24 km远.
(3)为了尽快抢救灾民，冲锋舟出发前就加满了油，而且在救灾过程中不再加油，若冲锋舟每千米耗油0.5升，那么该冲锋舟油箱容量至少是多少升？
【解】冲锋舟当天航行总路程为｜+14｜+｜-10｜+｜+8｜+｜-7｜+｜+13｜+｜-6｜+｜+12｜+｜-6｜＝14＋10＋8＋7＋13＋6＋12＋6＝76(km).76×0.5＝38(升).所以该冲锋舟油箱容量至少是38升.
13. [母题·教材P71复习题T6·新视角结论开放题]还记得小时候经常玩的填数游戏吗？一起用有理数来试试吧！(1)请在图①的各个圆圈内填上适当的数，使每个圆圈内的数都等于与它相邻的2个数的和.
(2)如图②，在圆圈内填上恰当的数，使每条线上的3个数之和为0.
【解】如图②所示，答案不唯一.
(3)将图②中心处的0改为－5，如图③，那么怎样填写才能使每条线上的3个数之和为－15？
【解】如图③所示，答案不唯一.
14. [新视角·新定义题·2024·石家庄长安区期末]对于一个非整数的有理数 x ( x ≠ n ＋0.5， n 为整数)，我们规定：( x )表示不大于 x 的最大整数，[ x ]表示不小于 x 的最小整数，{ x }表示最接近 x 的整数.例如，(3.14)＝3，[3.14]＝4，{3.14}＝3，则使3( x )＋2[ x ]＋{ x }＝20成立的 x 的取值范围为(　A　)
由题意，大致判断出3＜ x ＜4，且 x ≠3.5.
当3.5＜ x ＜4时，( x )＝3，[ x ]＝4，{ x }＝4，
所以3( x )＋2[ x ]＋{ x }＝9＋8＋4＝21≠20，不符合题意，排除B，C；
当3＜ x ＜3.5时，( x )＝3，[ x ]＝4，{ x }＝3，
所以3( x )＋2[ x ]＋{ x }＝9＋8＋3＝20，符合题意.
有理数加法法则:1.同号两数相加，取相同的符号，并把绝对值相加2.异号两数相加，绝对值相等时和为0；绝对值不等时，取绝对值较大的数的符号，并用较大的绝对值减去较小的绝对值3.一个数同0相加，仍得这个数
有理数加法法则的运用:1.首先判断加法类型; 2.再确定和的符号;3.最后确定和的绝对值