专题39 空间直线、平面的垂直-2025年高考数学一轮复习讲义（知识梳理+真题自测+考点突破+分层检测）（新高考专用）

这是一份专题39 空间直线、平面的垂直-2025年高考数学一轮复习讲义（知识梳理+真题自测+考点突破+分层检测）（新高考专用），文件包含专题39空间直线平面的垂直-2025年高考数学一轮复习讲义知识梳理+真题自测+考点突破+分层检测新高考专用原卷版docx、专题39空间直线平面的垂直-2025年高考数学一轮复习讲义知识梳理+真题自测+考点突破+分层检测新高考专用解析版docx等2份试卷配套教学资源，其中试卷共84页， 欢迎下载使用。
【知识梳理】2
【真题自测】3
【考点突破】6
【考点1】直线、平面垂直的判定与性质6
【考点2】平面与平面垂直的判定与性质8
【考点3】平行、垂直关系的综合应用11
【分层检测】13
【基础篇】13
【能力篇】16
【培优篇】17
考试要求：
从定义和基本事实出发，借助长方体，通过直观感知，了解空间中直线与直线、直线与平面、平面与平面的垂直关系.
知识梳理
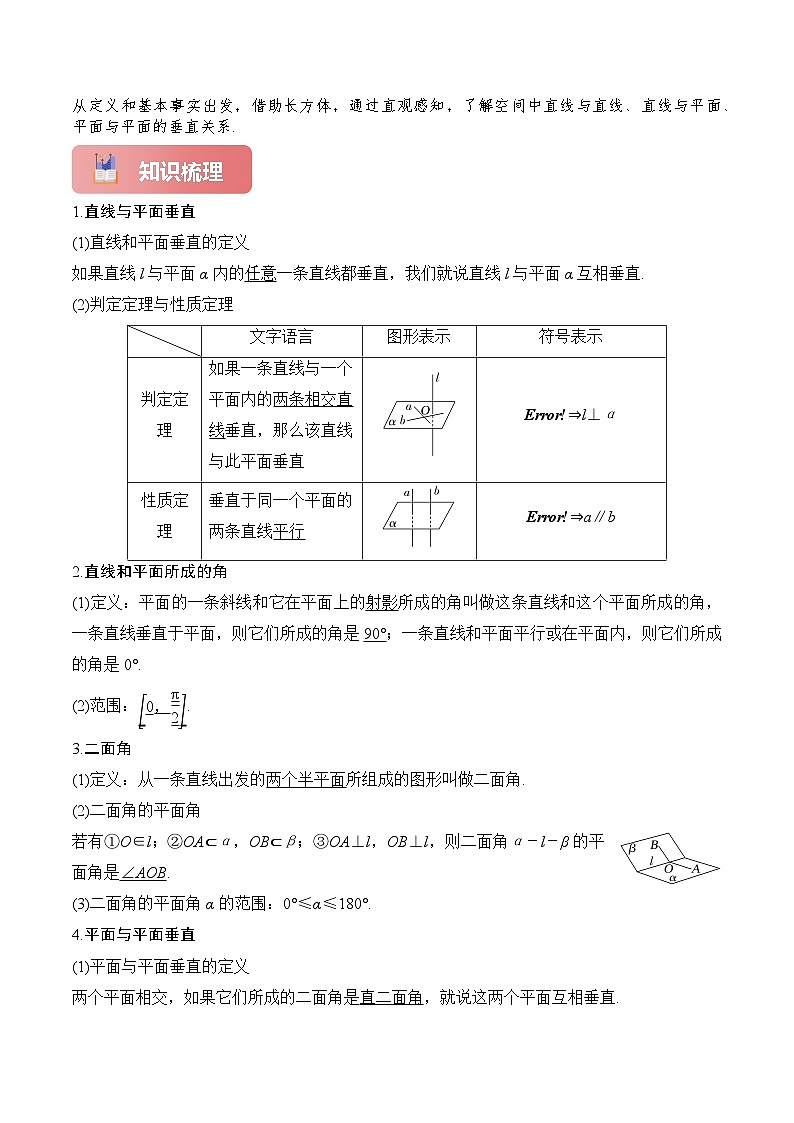
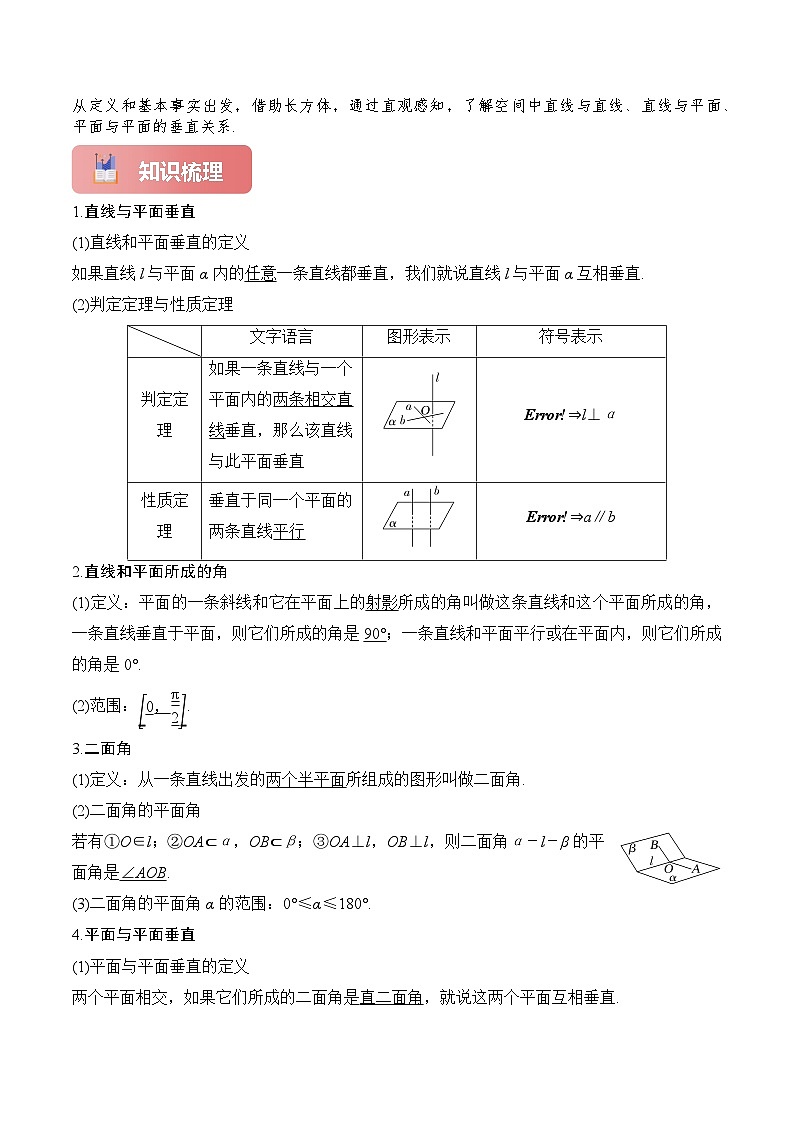
1.直线与平面垂直
(1)直线和平面垂直的定义
如果直线l与平面α内的任意一条直线都垂直，我们就说直线l与平面α互相垂直.
(2)判定定理与性质定理
2.直线和平面所成的角
(1)定义：平面的一条斜线和它在平面上的射影所成的角叫做这条直线和这个平面所成的角，一条直线垂直于平面，则它们所成的角是90°；一条直线和平面平行或在平面内，则它们所成的角是0°.
(2)范围：eq \b\lc\[\rc\](\a\vs4\al\c1(0，\f(π,2))).
3.二面角
(1)定义：从一条直线出发的两个半平面所组成的图形叫做二面角.
(2)二面角的平面角
若有①O∈l；②OA⊂α，OB⊂β；③OA⊥l，OB⊥l，则二面角α－l－β的平面角是∠AOB.
(3)二面角的平面角α的范围：0°≤α≤180°.
4.平面与平面垂直
(1)平面与平面垂直的定义
两个平面相交，如果它们所成的二面角是直二面角，就说这两个平面互相垂直.
(2)判定定理与性质定理
1.三个重要结论
(1)若两平行线中的一条垂直于一个平面，则另一条也垂直于这个平面.
(2)若一条直线垂直于一个平面，则它垂直于这个平面内的任何一条直线(证明线线垂直的一个重要方法).
(3)垂直于同一条直线的两个平面平行.
2.三种垂直关系的转化
真题自测
一、单选题
1．（2024·北京·高考真题）如图，在四棱锥中，底面是边长为4的正方形，，，该棱锥的高为（ ）.
A．1B．2C．D．
2．（2024·全国·高考真题）已知正三棱台的体积为，，，则与平面ABC所成角的正切值为（ ）
A．B．1C．2D．3
3．（2023·北京·高考真题）坡屋顶是我国传统建筑造型之一，蕴含着丰富的数学元素．安装灯带可以勾勒出建筑轮廓，展现造型之美．如图，某坡屋顶可视为一个五面体，其中两个面是全等的等腰梯形，两个面是全等的等腰三角形．若，且等腰梯形所在的平面、等腰三角形所在的平面与平面的夹角的正切值均为，则该五面体的所有棱长之和为（ ）

A．B．
C．D．
4．（2023·天津·高考真题）在三棱锥中，点M,N分别在棱PC,PB上，且，，则三棱锥和三棱锥的体积之比为（ ）
A．B．C．D．
二、解答题
5．（2024·北京·高考真题）如图，在四棱锥中，，，,点在上，且，．
(1)若为线段中点，求证：平面．
(2)若平面，求平面与平面夹角的余弦值．
6．（2024·全国·高考真题）如图，平面四边形ABCD中，，，，，，点E，F满足，，将沿EF翻折至，使得．
(1)证明：；
(2)求平面PCD与平面PBF所成的二面角的正弦值．
7．（2024·全国·高考真题）如图，四棱锥中，底面ABCD，，．
(1)若，证明：平面；
(2)若，且二面角的正弦值为，求．
8．（2023·北京·高考真题）如图，在三棱锥中，平面，．

(1)求证：平面PAB；
(2)求二面角的大小．
9．（2023·全国·高考真题）如图，在三棱锥中，，，，，的中点分别为，点在上，．
(1)求证：//平面；
(2)若，求三棱锥的体积．
10．（2023·全国·高考真题）如图，在三棱柱中，底面ABC，，到平面的距离为1．

(1)证明：；
(2)已知与的距离为2，求与平面所成角的正弦值．
考点突破
【考点1】直线、平面垂直的判定与性质
一、单选题
1．（2024·陕西商洛·模拟预测）如图，四边形是圆柱的轴截面，是底面圆周上异于，的一点，则下面结论中错误的是（ ）
A．
B．平面
C．平面平面
D．平面
2．（2024·辽宁大连·一模）已知直线a，b，c是三条不同的直线，平面α，β，γ是三个不同的平面，下列命题正确的是（ ）
A．若，则
B．若，则
C．若，且，则
D．若，且，则
3．（23-24高三上·四川·阶段练习）已知l，m是两条不同的直线，，是两个不同的平面，则下列命题中正确的是（ ）
A．若，，，则
B．若，，则
C．若，，，则
D．若，且与所成的角和与所成的角相等，则
二、多选题
4．（2024·湖南邵阳·三模）如图所示，点为正方体形木料上底面的动点，则下列结论正确的有（ ）
A．三棱锥的体积为定值
B．存在点，使平面
C．不存在点，使平面
D．经过点在上底面上画一条直线与垂直，若与直线重合，则点为上底面中心
三、解答题
5．（2024·天津河北·模拟预测）如图，在四棱锥中，底面是正方形，平面，，，分别是，的中点．
(1)求证：平面；
(2)求证：平面；
(3)求直线与平面所成角的正弦值．
6．（2024·山东济宁·三模）图1是由正方形ABCD和两个正三角形组成的一个平面图形，其中，现将沿AD折起使得平面平面，将沿CD折起使得平面平面，连接EF，BE，BF，如图2.
(1)求证:平面；
(2)求平面与平面夹角的大小.
反思提升：
(1)证明线面垂直的常用方法：①判定定理；②垂直于平面的传递性；③面面垂直的性质.
(2)证明线面垂直的关键是证线线垂直，而证明线线垂直，则需借助线面垂直的性质.
【考点2】平面与平面垂直的判定与性质
一、单选题
1．（2024·四川成都·三模）已知直线、、与平面、，下列命题正确的是（ ）
A．若，，则
B．若，，则
C．若，，则
D．若，，，则
2．（2024·江西鹰潭·模拟预测）如图，在长方形中，，，E为DC的中点，F为线段EC（端点除外）上的动点．现将沿AF折起，使平面平面，在平面内过点D作，K为垂足．设，则t的取值范围是（ ）
A．B．C．D．
二、多选题
3．（2022·江苏泰州·模拟预测）在正四棱锥中，点分别是棱上的点，且，，，其中，则（ ）
A．当时，平面平面
B．当，，时，平面
C．当，，时，点平面
D．当，时，存在，使得平面平面
4．（2024·江苏泰州·模拟预测）在正三棱柱中，的重心为，以为球心的球与平面相切．若点在该球面上，则下列说法正确的有（ ）
A．存在点和实数，使得
B．三棱锥体积的最大值为
C．若直线与平面所成的角为，则的最大值为
D．若，则所有满足条件的点形成的轨迹的长度为
三、解答题
5．（2024·江西新余·二模）如图，在四棱锥中，底面是直角梯形，，，且，.

(1)若为的中点，证明：平面平面；
(2)若，，线段上的点满足，且平面与平面夹角的余弦值为，求实数的值.
6．（2024·湖南衡阳·模拟预测）如图，在三棱柱中，平面平面，平面平面．
(1)证明：平面ABC．
(2)若，，求直线BC与平面所成角的正弦值．
反思提升：
(1)面面垂直判定的两种方法与一个转化
①两种方法：
(i)面面垂直的定义；
(ii)面面垂直的判定定理(a⊥β，a⊂α⇒α⊥β).
②一个转化：
在已知两个平面垂直时，一般要用性质定理进行转化.在一个平面内作交线的垂线，转化为线面垂直，然后进一步转化为线线垂直.
(2)面面垂直性质的应用
①两平面垂直的性质定理是把面面垂直转化为线面垂直的依据，运用时要注意“平面内的直线”.
②两个相交平面同时垂直于第三个平面，它们的交线垂直于第三个平面.
【考点3】平行、垂直关系的综合应用
一、单选题
1．（2024·浙江宁波·模拟预测）已知棱长为1的正方体分别是AB和BC的中点，则MN到平面的距离为（ ）
A．B．C．D．
2．（23-24高三上·陕西商洛·阶段练习）如图所示，在棱长为2的正方体中，点在棱上，且，则点到平面的距离之和为（ ）

A．B．C．D．
二、多选题
3．（2023·湖南长沙·模拟预测）如图1，某广场上放置了一些石凳供大家休息，这些石凳是由正方体截去八个一样的正三棱锥得到的，它的所有边长均相同，数学上我们称之为半正多面体（semiregular slid），亦称为阿基米德多面体，如图2，设，则下列说法正确的是（ ）

A．该多面体的表面积为
B．该多面体的体积为
C．该多面体的平行平面间的距离均为
D．过A、Q、G三点的平面截该多面体所得的截面面积为
4．（2024·山西晋中·模拟预测）如图，在棱长为2的正方体中，G为的中点，则下列结论正确的有（ ）
A．CG与所成角的余弦值为
B．与平面的交点H是的重心
C．三棱锥的外接球的体积为
D．与平面所成角的正弦值为
三、解答题
5．（2024·四川成都·模拟预测）如图所示，斜三棱柱的各棱长均为， 侧棱与底面所成角为，且侧面底面．

(1)证明：点在平面上的射影为的中点；
(2)求二面角的正切值．
6．（2024·全国·模拟预测）如图四棱台中，，平面，.
(1)证明：；
(2)若，，，求二面角的余弦值.
反思提升：
三种垂直的综合问题，一般通过作辅助线进行线线、线面、面面垂直间的转化.求解时应注意垂直的性质及判定的综合应用.如果有平面垂直时，一般要用性质定理，在一个平面内作交线的垂线，使之转化为线面垂直，然后进一步转化为线线垂直.
分层检测
【基础篇】
一、单选题
1．（2024·陕西安康·模拟预测）已知正三棱台的上底面积为，下底面积为，高为2，则该三棱台的表面积为（ ）
A．B．C．D．18
2．（2023·全国·模拟预测）已知正方体的棱长为1，点O在线段上且，则点O到平面的距离是（ ）
A．B．C．D．
3．（2024·陕西安康·模拟预测）在四棱锥中，为等边三角形，四边形为矩形，且，平面平面，则直线AC与平面所成角的正弦值为（ ）
A．B．C．D．1
4．（2024高三下·全国·专题练习）已知m，n是两条不同的直线，是三个不同的平面，则下列命题正确的是（ ）
A．平面内有无数条直线与平面平行的充要条件是
B．平面内有两条直线m，n分别与平面平行，则
C．若，且，则
D．平面内有无数条直线与平面垂直，则
二、多选题
5．（2024·河南·模拟预测）已知点，为不同的两点，直线，，为不同的三条直线，平面，为不同的两个平面，则下列说法正确的是（ ）
A．若，，则
B．若，，则
C．若，，，，则
D．若，，，，则直线
6．（2023·云南·三模）下列说法错误的是（ ）
A．若直线不平行于平面，，则内不存在与平行的直线
B．若平面平面，平面平面，，则
C．设为直线，在平面内，则“”是“且”的充分不必要条件
D．若平面平面，平面平面，则平面与平面所成的二面角和平面与平面所成的二面角相等或互补
7．（2022·江苏泰州·模拟预测）在正四面体A－BCD中，，点O为的重心，过点O的截面平行于AB和CD，分别交BC，BD，AD，AC于E，F，G，H，则 （ ）
A．四边形EFGH的周长为8
B．四边形EFGH的面积为2
C．直线AB和平面EFGH的距离为
D．直线AC与平面EFGH所成的角为
三、填空题
8．（2024·陕西·三模）如图，四边形是圆柱的轴截面，是底面圆周上异于的一点，则下面结论中正确的序号是 ．（填序号）
①；②；③平面；④平面平面．
9．（23-24高三下·重庆·开学考试）如图，在正四棱柱中，为的中点，则中点到平面的距离为 ．
10．（1997·全国·高考真题）已知m、l是直线，α、β是平面，给出下列命题：
①若l垂直于α内两条相交直线，则；
②若l平行于α，则l平行于α内所有的直线；
③若，且，则；
④若且，则；
⑤若，且，则．
其中正确命题的序号是 ．
四、解答题
11．（2024·上海普陀·二模）如图，在四棱锥中，底面是边长为1的正方形，，、分别是、的中点.
(1)求证：平面；
(2)若二面角的大小为，求直线与平面所成角的大小.
12．（2024·江苏·二模）如图，直三棱柱的体积为1，，，．
(1)求证：；
(2)求二面角的余弦值．
【能力篇】
一、单选题
1．（2024·陕西·模拟预测）在平行六面体中，已知，，则下列选项中错误的一项是（ ）
A．直线与BD所成的角为90°
B．线段的长度为
C．直线与所成的角为90°
D．直线与平面ABCD所成角的正弦值为
二、多选题
2．（2024·湖北武汉·模拟预测）如图，在正方体中，分别为棱的中点，点是面的中心，则下列结论正确的是（ ）
A．四点共面B．平面被正方体截得的截面是等腰梯形
C．平面D．平面平面
三、填空题
3．（2024·全国·模拟预测）如图，已知平面平面，，，，，则异面直线与所成角的余弦值为 .
四、解答题
4．（2024·山东青岛·三模）如图所示，多面体，底面是正方形，点为底面的中心，点为的中点，侧面与是全等的等腰梯形，，其余棱长均为2.
(1)证明:平面；
(2)若点在棱上，直线与平面所成角的正弦值为，求.
【培优篇】
一、单选题
1．（2024·北京·三模）故宫角楼的屋顶是我国十字脊顶的典型代表，如图1，它是由两个完全相同的直三棱柱垂直交叉构成，将其抽象成几何体如图2所示.已知三楼柱和是两个完全相同的直三棱柱，侧棱与互相垂直平分，交于点I，，，则点到平面的距离是（ ）

A．B．C．D．
二、多选题
2．（23-24高二上·浙江金华·期末）“阿基米德多面体”也称为半正多面体，是由边数不全相同的正多边形为面围成的多面体，它体现了数学的对称美.如图，是一个八个面为正三角形，六个面为正方形的“阿基米德多面体”，某玩具厂商制作一个这种形状棱长为，重量为的实心玩具，则下列说法正确的是（ ）

A．将玩具放到一个正方体包装盒内，包装盒棱长最小为.
B．将玩具放到一个球形包装盒内，包装盒的半径最小为.
C．将玩具以正三角形所在面为底面放置，该玩具的高度为.
D．将玩具放至水中，其会飘浮在水面上.
三、填空题
3．（2024·河北保定·三模）在三棱锥中，已知是边长为2的正三角形，且.若和的面积之积为，且二面角的余弦值为，则该三棱锥外接球的表面积为 .
文字语言
图形表示
符号表示
判定定理
如果一条直线与一个平面内的两条相交直线垂直，那么该直线与此平面垂直
eq \b\lc\ \rc\}(\a\vs4\al\c1(l⊥a,l⊥b,a∩b＝O,a⊂α,b⊂α))⇒l⊥α
性质定理
垂直于同一个平面的两条直线平行
eq \b\lc\ \rc\}(\a\vs4\al\c1(a⊥α,b⊥α))⇒a∥b
文字语言
图形表示
符号表示
判定定理
如果一个平面过另一个平面的垂线，那么这两个平面垂直
eq \b\lc\ \rc\}(\a\vs4\al\c1(l⊥α,l⊂β))⇒α⊥β
性质定理
两个平面垂直，如果一个平面内有一直线垂直于这两个平面的交线，那么这条直线与另一个平面垂直
eq \b\lc\ \rc\}(\a\vs4\al\c1(α⊥β,α∩β＝a,l⊥a,l⊂β))⇒l⊥α